1998-11-12[n年前へ]
■無限音階を作ろう 
上昇し続けるって何ですか?
無限音階を作りたい
無限音階というものがある。ド・レ・ミ・・・と音がどんどん高くなっていくように聞こえるのだが、いつまでたっても終わらず、ふと気づくとずっと前と同じような音の高さだというものである。Escherの無限階段の版画は有名だが、あれの音階版である。とにかく、無限音階を作ってみようというのが今回の目的である。参考までに、Eshcerのことに関しては藤原康司氏のWEBhttp://www.pluto.dti.ne.jp/~fwhd5468/に詳しい情報がある。 ちなみに、このような版画である。
 |  | 「上昇と下降」(左図、1960年作) 「滝」(右図、1961年作) |
無限音階の仕組み
人間の聴力にはもちろん周波数特性がある。ニコンの補聴器のWEBhttp://www.nikon.co.jp/main/jpn/society/hocyouki.htm
によれば20Hz-20kHzが通常聞こえる周波数の範囲であるという。例えば、CDのサンプリング周波数はが約40kHzであるのは、この20kHzの倍だからである。つまり、ナイキスト周波数による。
もし、ある高さの「ド」の1オクターブ下、そのまた下、...それだけでなく、1オクターブ上、そのまた上...が一度になったら、人間の耳にはどう聞こえるだろうか。それは、やはり「ド」である。その時のスペクトルはこんな感じである。なお、横軸は2をベースにした変形の対数軸である。また、実際には「ド」ではない。
 |
それでは、そのような「レ」が鳴ったとしたら?もちろん、それも「レ」である。そのようにして、「ドレミファソラシド」とやるとどうだろう?最初の「ド」と最後の「ド」は全く同じになっている。しかし、人間の感覚としてはどんどん音の高さが上昇していくように感じる。これが無限音階の仕組みである。
図で示すとこのようになる。なお、下の図中で水色は人間の耳に聞こえる周波数領域である。また、振幅はたんなる相対値である。
 |
 |
 |
 |
 |
作成した無限音階
今回は12音の平均率音階を用いている。音階そのものについては「音階について考える」という別の話である。また、基本波形としては正弦波を用いている。20Hz以下の正弦波を基本波形として、その倍音を20kHz超まで均等に足しあわせたものをただ作っただけである。正弦波を用いたのは話を単純化するためである。ここに今回作成したMathematicaのNoteBookを置いておく。また、下が作成する途中のデータである。どこか間違っているような気もする。少し不安だ。
 |  |
 |  |
さて、これが作成した無限音階である。それっぽく聞こえるだろうか。
1999-09-23[n年前へ]
■MiosoftはApple株でいくら儲けているか? 
価値観は線形なままで
ユング心理学では因果関係が無い偶然の一致を「シンクロニシティ(共時性)」と呼ぶ。いろいろ意見の違いもあるだろうが、私は「シンクロニシティ(共時性)」は結局偶然のせいではなく、世の中の流れの要請による必然なのではないかと思うのである。
と、いきなり訳のわからない話だが、今回の話は「今日の必ずトクする一言」の
ともあれ、webmaster氏のメールのおかげで、株価の値軸が妙に頭に残る最中に、私は「MicrosoftはApple株でいくら儲けているか?」という疑問が沸いて、Appleの株価を見に行ったのである。何しろ、MicrosoftはAppleの大株主である。
 |  |
一見似ているように思える。しかし、よく見てみると軸が違っている。左のAppleComputerの株価変動は対数軸で表されている。「株価表示グラフで値の軸を対数軸にできないか」という言葉が頭にあったせいで気づいたわけだ。そこで、この違いが新鮮で「今日の必ずトクする一言」のwebmaster氏への返信に至ったわけである。
それでは、左のAppleComputerの株価変動をリニアな軸に変換してみよう。
 |  |
印象が全く違う。右の線形軸のグラフは値軸の間隔が等間隔になっているのがわかると思う。それに対して対数軸で表されている右側は上に行くほど間隔が短い。右の線形軸では株価が急激に上昇しているのが実感できる(私は)。株取引的な考察は「対数軸証券グラフのナゾ」の方にあるので、ここでは本題の「MicrosoftはApple株でいくら儲けているか?」に戻る。
さて、このグラフのようにApple株は急上昇中なわけで、問題の「MicrosoftはApple株でいくら儲けているか?」であるが、97/08/08当時の13ドル前後の株価で一億五千万ドル分のApple株を買っていたとしたら、現在は80ドルくらいであるから、およそ6倍。すなわち、一億五千万ドルから九億ドルになっていることになる。うーん、たまらん。800億円近い差が有る(線形的な発想)。
さて、最初の疑問はこれで解決したのだが、わが「できるかな?」でも株価の軸の
- 対数軸
- 線形軸
日頃、実験を行っている時などは
「たかだか一桁の変化だろう。」などと対数軸の感覚に支配されているのであるが、こと経済になると線形軸の感覚に支配されるのである。これは私が貧乏であるからかもしれない。1万円はどんなときも1万円なのである。10万円と11万円の違いも、100万円と101万円の違いも同じなのだ。これが一億円と一億一万円でも同じである。何しろ、そんなお金と無縁なのである。であるから、貧乏な金銭感覚をそのまま線形で延長してしまうのである。「金銭に関する差の感覚」といってもよい。
これは人によっても違うだろう。私と違うブルジョアジーな人であれば、例えば、車を買うときに
「300万円の車を買うから、30万円のカーナビを一緒に買っても誤差みたいなものだ。」という人もいると思う。また、「一億円と一億一万円は同じだ」と言うだろう。これなどは経済に関する対数軸の感覚の一種だと思う。この人は「金銭に関する比の感覚」を持つ人である
さて、こういうことを考えていくと、金持ちの1万円と私の1万円は価値が違うことにいまさらながら気づくのである。私は1万円もらったら大喜びだ。しかし、同じだけビル・ゲイツを喜ばせようと思ったら、九億ドル位は必要だろう。そういうことを考えると、経済社会は実に対数軸である。いや、むしろ世の中が対数軸だと言ったほうが良いだろうか?
今回の話とやはり似て非なる話がロゲリギストの「第四物理の散歩道」の「理解の形式」に述べられているので、興味の有る方は読むと面白いと思う。
さてさて、同じ題材をとってみても経済オンチの私が作る「できるかな?」は「「対数軸株価グラフのナゾ」」とは違い、ずいぶんと変な話になってしまったようである。しかし、それが個性というもの。みんなが同じではつまらない。
ともあれ、価値観に対する評価軸は線形軸の方が良い、と思う私であった。
1999-12-04[n年前へ]
■WEBの世界の「力の法則」 
「ReadMe!JAPAN」と「日記猿人」に見るWEBアクセス数分布
以前、
の中で書いたように、「Webの成長のダイナミクスとトポロジは,物理学の世界のPower(累乗)Lawとして知られている法則に従っている」という面白い話が世の中にはある。これは、「ごく少数のWEBサイトへのアクセス、あるいはリンクが他を圧倒する程の割合を示す。」ということである。「インターネットのほとんどのアクセスというものは、ごく少数の特定のサイトへのものである。」ということだ。宇多田ヒカルの売り上げが演歌の総売上をはるかに超えるという話とよく似ている。実社会でもそういうことは実に多い。どうも、マイナー趣味である私には、Power(累乗) Lawというのはいま一つ面白くない話ではあるが、
- InternetEcologies
- http://www.parc.xerox.com/spl/groups/dynamics/www/internetecologies.html
- Paperson small-world networks
- http://www.ncrg.aston.ac.uk/~vicenter/smallworld.html
まずは、考えるためのデータを採取してることにした。欲しいデータは色々なWEBサイトへのアクセス数である。もちろん、自分のWEBサイトへのアクセスではないのだから、何らかの公開データを探さなければならない。
そこで、ReadMe!Japan(http://readmej.com/)と日記猿人(http://wafu.netgate.net/ne/)という二つのランキングシステムを用いてみた。ReadMe!Japanは日本語の「読み物」を主体としたWEBランキングである。また、日記猿人は名前の通り「日記」をターゲットとしたWEBランキングである。
一見、同じように見えるReadMe!Japanと日記猿人のランキングであるが、かなり違ったシステムである。以下に、Readme!Japanと日記猿人のランキングシステムを示してみる。
- Readme!Japan 登録したWEBページに、一日の間にアクセスしたIPアドレスの数。
- 日記猿人 「投票」ボタンを押した人(ブラウザー)の数、一日の間に一人の人(ブラウザー)が同一の日記に対して複数回の投票は行うことが出来ない。
一方、Readme!JapanはIPアドレスベースであるから、同一のProxyなどを経由したアクセスの場合、何人からアクセスがあろうと1pointである。しかし、読者に「投票ボタンを押す」というような作業は要求されない。
それでは、日記猿人とReadMe!JAPANの得票ランキングの例を示してみる。横軸はランク(順位)であり、縦軸が得票数である。ここでは縦軸・横軸共に線形軸を用いている。
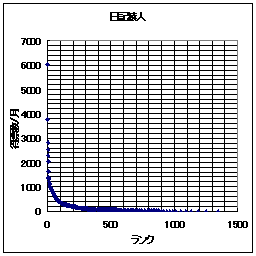 | 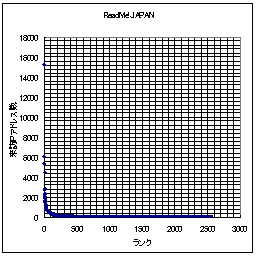 |
なお、 Readme!Japanは11/30日のものであり、日記猿人は(ほぼ)11月分の得票数分である。
このグラフを眺めてみると、日記猿人とReadMe!JAPAN共によく似ている。なるほど、少しランクが下がっただけで、急激に得票数が少なくなっている。もう、縦軸で言うならば下に張りついてしまっている。「ごく少数のWEBサイトへのアクセス、あるいはリンクが他を圧倒する程の割合を示す。」という「WEBの世界の力(累乗)の法則」は日記猿人とReadMe!JAPANでも当てはまるようである。
さて、ここまでランクに対して得票数が変化するとなると、グラフの軸は線形軸でなくて対数軸の方が良いだろう。そこで、グラフの軸を対数軸に変えたものを以下に示す。
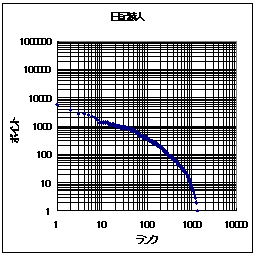 |  |
こうすると、日記猿人とReadMe!JAPANのどちらも、
- 上位のランク(例えば、1位から1000位程度まで)では傾きがほぼ1である。すなわち、ランクが一桁下がると、アクセス数も一桁下がる。
また、ReadMe!JAPANでは、ランクが極めて大きい所では得票数が0に近い。おそらく、その影響と考えられるが、ランクと得票数の関係が直線でなくなっている。
それと同じことは日記猿人でも言えるだろう、ただし、「ランクとポイントの関係が直線でなくなる」のがReadMe!JAPANよりも早いような気がする。しかし、それは誤差かもしれない。参加数もかなり異なっているので、誤差の可能性が高いと思われる。
さて、これまでは日記猿人とReadMe!JAPANのランキングの数字を直接用いてきたわけである。しかし、得票数の全く違うものをそのまま比較してもしょうがない。ある程度条件をそろえた上で比較をすべきであろう。そこで、縦軸を正規化して比較をしてみることにした。得票数の合計が1であるような単位に変換してみるのである。
ここで、横軸はランクのLog_10を用いている。本来、ランク(順位)も何らかの正規化の変換をすべきであろうが、今回はやり忘れた。きっと、頭が疲れているせいである。
また、グラフを見ればわかると思うが、それぞれについて近似曲線を計算している。
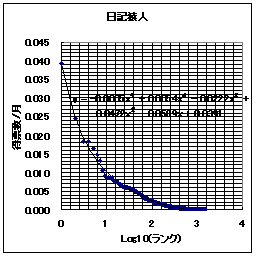 | 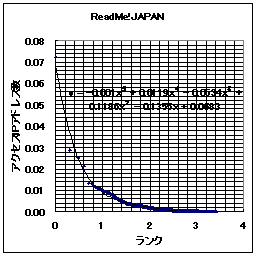 |
次に、ここで得られた「ランクとポイントの関係」を示す近似関数
- ReadMe!JAPAN y = -0.001x^5 + 0.0119x^4 - 0.0534x^3 + 0.1186x^2 - 0.1355x+ 0.0683
- 日記猿人 y = -0.0005x^5 + 0.0054x^4 - 0.0222x^3 + 0.0472x^2 - 0.0589x+ 0.0391
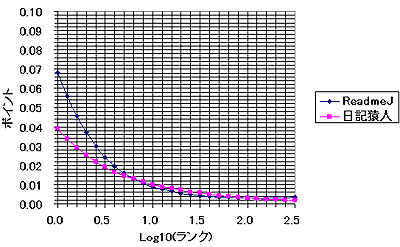 |
R eadMe!JAPANでも日記猿人でも横軸が2以上(すなわち100位以下)の場所などでは、ほとんどポイントはゼロみたいなものである。すなわち、100位より下のWEBのアクセス(本WEBへのアクセスも含めて)は誤差みたいなものなのだ。何しろ、一位(トップ)のポイントが0.07とか0.04とかなのだ。それは「一位のWEBサイトへのアクセスが全部のサイトへのアクセスの1割弱を占める」ということなのである。20位までのサイトへのアクセスを合計すると全アクセスの50%以上を占めてしまう。これが、恐るべきWEBの世界の"PowerLaw"、すなわち、「力(累乗)の法則」である。
ところで、日記猿人では上位サイト(すなわち、横軸で0に近いところ)での関係式の傾きがReadMe!JAPANよりも小さい。すなわち、上位サイトの得票数が拮抗している。これは一体何故だろうか?
私はこの理由を、
- 日記猿人の読者が割と似ている趣味を持っている
- 日記猿人の参加WEBサイトが似たような内容を持っている
日記猿人の参加WEBサイトが似ており、読者同士が割と似ている趣味を持っていれば(私も含めて)、得票数というのは当然横並びになるだろう。上位サイトにはほとんどの人が見に行き、そしてほとんどの人が「投票」ボタンを押せば、上位サイトはみな同じような得票数を示すことになる、と思うのである。
それは、違う傾向を示すReadMe!JAPANの中でも、読者層も作者も似ている「Fast&First」と「今日の必ずトクする一言」はとても近い得票数を示している、ということがその根拠の一つである。
それに対して、ReadMe!JAPANが比較的広いジャンルの「読み物」が集まっているのでそういう現象が見られないのだろう、と考えるのである。しかも、実際には「読み物」ですらないものも集まっているので、なおさらジャンルとしてはバラけている。だから、「WEBの世界の力(累乗)の法則」を素直に反映していると考えるのである。
私としては、ごく一部のWEBサイトへの集中が生じるのはツマラナイと感じてしまうのであり、「WEBの世界の力(累乗)の法則」はキライである。だからといって、趣味が似た人ばかりというのもツマラナイように思う。うーん、どういうのがツマラナクナイのだろうか?
それはきっと、「色々な趣味の人が色々なWEBへアクセスする」というのが私の好みだ。実現は難しいのだろうけど...いや、そんなことはないか。
1999-12-30[n年前へ]
■6502と並列計算とムーアの法則 
人間のクロック&スケールアップ
「物理の散歩道」を読み直していると、とある文章に興味を覚えた。
- 第五物理の散歩道 ロゲルギスト著 岩波新書
「通信を考える」の中の興味を惹かれた部分は「信号の伝わる速度と距離と処理速度の関係」を論じている部分だ。例えば、計算機は処理速度を高めるためには回路の大きさを小さくしなければならないとか、人間の頭脳の働きの速さから集団生活の広がりの限界について論じているのだ。例えば、
- 計算機の演算速度の時間スケール -> ナノ秒 = 10^-9s (クロックで考えると、1GHz)
- 人間の演算速度の時間スケール -> サブ秒 = 10^-1s (クロックで考えると、10Hz)
つまり、通信の速度が光速度であるとして、演算の単位クロックの間に通信が行われなければならないとするならば、計算機の時間・空間スケールと人間の時間・空間スケールは等しいだろう、という推論だ。
そして、さらにロゲルギストの想像は広がり、並列計算についても論じている。
計算機が東京と大阪に離れて置かれていて、通信をしながら作業をするとしたら、人間の場合にはそれと同じ条件というのはどんなものだろうか、と彼らは考える。それは、光の速度で55時間、ちょうど冥王星の軌道直径の5倍程度の空間スケールになる、と論じている。それ以上、離れた場合には演算の過程を共に行うのは無理ではないかというのである。
こういう文章を読んでいると、この文章が作られたのが30年以上前であることを忘れてしまいそうである。この人達の思索の自由さに憧れを感じてしまう。この人達は、頭の中にタイムマシンにでも持っているのだろうか、と感じてしまうのだ。
ところで、私がコンピューターをいじるようになった頃は、Apple][の時代だった。といっても、私はお金があふれていたわけではないので、XXX電子でAplle][のコンパチ基盤を買って組み立てて使っていた。その基盤上の6502は1MHzで動いていた筈だ(あぁ、I/Oの6809派vs6502派の論争が懐かしい!)。
それから20年程たち、CPUのクロックスピードは1GHzを越えようとしている。20年で1000倍である。そして、その集積度は、ムーア(GordonMoore)の法則の「半導体の性能と集積は、18ヶ月ごとに2倍になる」に従っている。
それでは、人間はどうだろうか?人間の脳味噌のクロックがどの程度であるか測定されているかどうか、素人の私にはよくわからない。しかし、WEB上のデータとしては、例えば
- Mayo's Profile( http://www.ceres.dti.ne.jp/~mayo/profile.html )
ロゲルギストの時代、すなわち30年以上前、から現在のMayo's Profileの値がほとんど変わっていないように、人間の演算スピードは変わるようなものではない。それは、そうだろう。ヒトのクロックスピードや集積度といったものは、変えるわけにはいかない。当然である。CPUと違ってプロセスルールを変化させるというような訳にはいかないのだ。
それでは、演算性能を上げようとしたらどうするだろうか?そうなると、並列計算を行うのが自然だろう。単独のCPUの性能を上げるわけに行かなくても、共同作業を行えば、演算性能を上げることができる。
現代はほとんどの作業が共同作業で行われる。また、その共同作業も大人数が関わるようになってきている。それは、どんな業種でも同じだ。一人では、なかなかできないことが多くなっている。
それら共同作業、すなわち並列計算、を行う人達(例えれば並列計算機における各ノード)を増やし、それらの間の情報転送をすばやく行うことが多くの作業(計算)を行うための手順だろう。
そこで、
で用いた- 人口増加( http://www.t3.rim.or.jp/~kabutoya/KABHTML/Yoi/2-1.html )
 |
なるほど、人間界の並列計算機におけるノード数は増加している。そして、各ノード間の通信速度を調べるために、まずは、
- 来て、見て、触って、情報伝達
- ( http://www.f-jhs.fukuoka-edu.ac.jp/3-3/jyoho.html )
西暦 内容これを全部転送速度に直してみる。といっても、よくわからない部分も多いので、私が適当に決めてみる。それでは、その変化を示してみよう。とりあえず、ここ200年位の間のものを考える。
-4000 のろし
-2400 伝書鳩
-2300 馬による伝令制度
1837 モールス電信機
1876 ベグラハム=ベル電話機
1909 グリエルモ=マルコーン無線電話機
1973 Ethernet XeroxPARCで生まれる。(ちなみにEther=エーテル)
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
西暦 内容という感じだ。グラフにすると、
1837 モールス電信機 = 2bps
1909 グリエルモ=マルコーン無線電話機=10kbps
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
 |
こんな感じである。対数グラフにおいて直線的に情報伝送速度が速くなっている。この関係は結構きれいである。
別に意図してこういう数字にした訳ではないのだが、不思議なことである。
このようにして、人間(ノード)間の転送レートが高くなることにより、先のような人口増加に伴うトラフィック増加をしのぐことができていると考えることもできるかもしれない。そして、人間達の共同作業、すなわち並列計算、を行うだけのバススピードを確保しているのである。
最近、会社組織などで分社化とか事業分割とかの話題をよく耳にする。こういった時に、分割における時間と空間のスケールはよく考える必要があるだろう。分割が有効なのは、ほとんど独立なものを分割する場合のみである。並列計算における領域分割などと同じだ。
共同作業がほとんどなく、結果のみをやりとりすれば良いような場合には分割による効果はあるだろう。その一方で、同じ事業・作業を行っているところが、離れていては作業の効率は上がらない。もし、技術系の会社でそのようなことを行うのであれば、事業や部署を並列化した際の真面目なシミュレーション位は行うべきだろう。いや、別に深い意図はないけど。
こういったことは「新・闘わないプログラマ No.109 時代錯誤」に書かれていることとも少し似ているような気がする。
さて、1999/12/30-2000/1/1は野沢温泉で温泉&スキーである。2000年問題で会社に泊まり込む人も多いが、私はスキー場で泊まり込みである。同時期に野沢温泉に行く人がいるならば、ぜひ一緒に「スキー場の特殊相対性理論」について討論したいと思う(スキー場で)。
2000-03-09[n年前へ]
■飲み屋の音と1/fノイズ 
くつろぎの音響解析編
私は典型的なプロレタリアート(死語)である。そのせいか、高級(行ったことがないからわからないのだが)そうなバーは苦手である。しかし、安〜い居酒屋は大好きだ。むしろ、「愛している」と言っても良いくらいである。新宿西口の思い出横町なんかその最たるものだ。
ところで、飲み屋の喧噪の音を聞いていると、何故か心安らぐような気さえしてしまう。「飲み屋の喧噪の音」というのはノイズとしか言いようのない音であるが、そのノイズが何故か心安らぐのである。しかし、高級そうなバーでは心安らぐどころではないのである。
一体、この違いはどこにあるのだろうか?いや、もちろん私がビンボーであるせいと言ってしまえば、話は簡単である。しかし、それはあまりにも哀しすぎる(私にとって)。きっと、何か他の理由があるに違いない、と思うのである。そこで、「科学の力」で何か他の理由を探してみることにした。私がバーが苦手で、居酒屋が大好きな理由を探してみることにしたのである。
居酒屋の環境ノイズを聞いていると、私は何故か心が安らぐわけであるが、「心安らぐノイズ」と言えば、「/fノイズ」というものがある。1/fノイズは心地良さ・気持ちよさを感じる、とよく言われる。今回はこれに着目してみたい。私が居酒屋の音を聴くと心が安らぎ、バーの音を聴くと何故か緊張する理由が「お金」ではなくて、環境音の特性にあると考えてみるのである。私のプライドのためにもそうであって欲しいわけだ。
そこで、今回は典型的な飲み屋の環境音を音響解析をしてみたいと思う。そして、それが果たして1/fノイズになっているかどうか調べてみたいと思うのである。特に、同じ飲み屋でも居酒屋とバーの間に違いがあるかどうか調べてみるのである。
それでは、飲み屋の代表的なものとして
- 居酒屋
- バー
- キャバレー
- 効果音大全集 45 屋内ノイズII キングレコード
- WaveSpectra for Windows95/98/NT4( http://member.nifty.ne.jp/efu/ )
 |
 |
 |
これを見てみると、居酒屋とキャバレーはほぼ同じであり、300Hzより高い音に関しては周波数=fが高くなるに従い環境音のパワー密度が低下していることがわかる。しかもその低下の仕方は滑らかである。ここで、表示軸は共に対数軸であるので、居酒屋とキャバレーの環境音は1/fノイズに近いといっても良いだろう。
私が居酒屋の環境音を聞くと落ち着くのはこれが理由だったのである。安いから落ち着くのではなくて、環境音が1/fノイズであるから落ち着くのである。私がビンボーなせいではなくて、ちゃんとした科学的な理由があったのである。
それに対して、一番下のバーの環境音では少し様子が異なる。パワースペクトラムは滑らかでもないし、傾きも異なる。すでに、環境音は1/fノイズではなくなっている。これである。このせいで、私はバーでは落ち着かなかったのだ。そう、私がバーで落ち着かないのは私がビンボーなせいではなくて、バーの環境音が1/fノイズでないせいだったのである。
この三つの環境音の間の違いが判り易いように、この三つを重ねて表示してみる。表示色は
- 緑:居酒屋
- 青:キャバレー
- 紫:バー
 |
緑の居酒屋と青のキャバレーがほぼ同じパワースペクトラムであるのがわかると思う。それに対して、バーでは様子が異なり、明らかに環境音が1/fノイズではなくなっている。ずいぶんと不自然なパワースペクトラムであることが判ると思う。
この不自然さが故に私はバーの環境音を聴いていると、落ち着かないのである。そういうわけで、今回の結論は、
- 私は居酒屋の音を聞いていると心が安らぐが、バーの音を聴いていると緊張する
- その理由は私がビンボーなせいではなく、居酒屋とバーの環境音の違いによるものである
- その違いは居酒屋の環境音が1/fノイズであるのに対して、バーの環境音は1/fノイズではない
あれっ、そう言えば、キャバレーの環境音も1/fノイズってことは、私はキャバレーの環境音を聞いても心が安らぐのだろうか?うーん、行ったことがないからわからないや。