2000-12-10[n年前へ]
■「星の王子さま」の背景に 
ウワバミの中身を見てみよう
以前、
で、塚崎幹夫氏の「星の王子さまの世界 - 読み方くらべへの招待 -」に沿ってSaint-Exuperyの「星の王子さま」-Le petit prince -について考えてみた。その中で、「星の王子さま」の最初の方で登場する「ある星を滅亡させた三本のバオバブ」がナチズム・ファシズム・帝国主義であるという塚崎幹夫氏の意見を長々と紹介しているわけだが、先日その内容に関連して「三本のバオバブ」について枢軸国を意味しているのではないかとの記述がありましたが、同様の視点に立てば、これはまさしくファッショと見ることができるでしょう。何故なら、イタリアファシスタ党のシンボルは三本の薪を束ねたシンボルだったように記憶しています。単語としてのファッショは束ですね。古代ローマの団結を意味するシンボルだそうです。という実に興味深いメールを頂いた。
もし本当に、Saint-Exuperyが強い危機感を感じていた「三本のバオバブ」= Saint-Exuperyの友人達を危ない目に合わせているという「三本のバオバブ」とよく似ている「三本の薪」という図柄をファシズムがシンボルとして用いていたのなら、それはとても興味深い事実である。それは、Saint-Exuperyが「三本のバオバブ」を描いた時代背景の一つとして、とても重要なものとなるだろう。本来は神聖視されるバオバブの木を、Saint-Exuperyが恐怖の象徴として用いるきっかけの背景の一つとして考えることができるかもしれない。
というわけで、ファシスタ党のシンボルを調べて、Saint-Exuperyが「星の王子さま」を描いた時代背景を考えてみることにした。何しろ今から考えてみると実に残念なことに、私は高校以降に世界史を学んだことがないのである。だから、この時代の知識は全然無いに等しい。もし、ファシスタ党のシンボルを調べてみて、それが確かに「三本のバオバブ」を連想させるような「三本の薪」であるならば、それはとても興味深いことである。そして、もしそうでなかったとしても、ファシスタ党のシンボルを調べる中でSaint-Exuperyが「星の王子さま」を描いた時代背景を知ることができるならば、それはそれで面白いことだと思うのだ。
そこで、イタリアファシスタ党の名前の由来とそのシンボルに関する情報をネット上でつらつらと眺めてみた。すると、ファシスタ党の名前の由来の方は情報も多く、簡単にまとめてしまうと
ファシスタ党の名前はイタリアのファシスタ党の前身であるファシストの団体FasciItaliani di Combattimentoに由来する。fasci(fascio)は元来は「束」「団結」を意味するものであり、そもそもの語源は古代ローマの執政官が持つ権威・権力の象徴で、斧の周りに鞭を束ねたfasces(fasciolittorio)に遡るというようなことを知ることができた。
そしてその名前の由来ともなったシンボルの図案の方は最初はなかなか見つからなかったが、fascesというキーワードで探してみることで
- Flags Of The World (http://www.crwflags.com/fotw/flags/ )
- The Italian Social Republic( http://www.cifr.it/Chapter_05.html )
 ( リンク先はhttp://www.crwflags.com/fotw/images/it-isr.gif ) |
この旗の中の鷲の足が掴んでいるのが「斧の周りに鞭を束ねたfasces」である。といっても、このサイズではよく判りにくいのでこの図を拡大してみたのが次の図である。
 ( リンク先はhttp://www.crwflags.com/fotw/images/fr-fasc.gif ) |
先程の「斧の周りに鞭を束ねた」という記述でもそうだったが、これを見ていると、少なくともファシスタ党のシンボルでありその名前の由来ともなったというファスケスはあくまで「斧の周りに木を束ねたもの」であって、「三本の薪」というわけではないようだ。
ということは、「三本の薪」→「三本のバオバブ」という連想をSaint-Exuperyがしたということは可能性としては無さそうだと思われる。「三本の薪」→「三本のバオバブ」というのは実に素直な連想なので本当なら面白そうだと思ったわけであるが、残念ながらそういうわけではないようだ。
ただ、「三本」という数字自体はナチズム・ファシズム・帝国主義の計三つの国・主義を示すものであるとしたら、「ファシズムのシンボルとしての木」→「恐怖の象徴としてのバオバブ」という連想が働いたと考えることも無理でないのかもしれない。
ところで、このファスケスを眺めていると、「星の王子さま」の冒頭に描かれている獲物に巻き付き飲み込もうとしてるウワバミを私は連想した。少しばかりではあるが、形が似ているように私には思えたのである。いや、形が似ていると言うよりは「似た雰囲気」を「ウワバミ」と「斧の周りに束ねられた木」の間に感じたのかもしれない。
 |
「星の王子さま」はこの画をきっかけとして、主人公のパイロットが「ウワバミの中身が見える人」= 「ほんとうにもののわかる人」とこれまで出会わなかった、という話が語られていく。そして、「大切なことは目に見えない」という言葉に繋がっていくのである。この言葉は決してメルヘンチックな言葉などではなくて、この言葉の中には何らかの強い意識が感じられるはずだ。
今回調べてみたファスケスは「結束」とか「権威・権力」を意味するが、その「結束」「権威・権力」のどちらが先に生まれたものなのかは私には判らない。だが、その「結束」「権威・権力」で飾られた内側は時として隠されがちになる。あるいはその内側を見る眼は時として曇りがちになるせいかもしれない。やはりここでも「ウワバミの中身」を見抜く眼を磨くことが必要とされる。かといって、「結束」「権威・権力」に単に批判的になるだけではそれは独りよがりにも陥りがちである。結局のところ、外にも内にも常に問いかけの眼を向けることが「ウワバミの中身が見える人」になるためには必要とされるのではないか、と私は思うのである。
2000-12-24[n年前へ]
■A型vB型・大戦争 
血液型分布を眺めてみよう
今年も私の職場には新入社員が入ってきた。その新入社員の中の一人は「血液型+ 動物占い」の信者だった。何しろ、ことあるごとに「血液型 + 動物占いの結果が同じ人はとってもよく似ているんですよ!もうビックリするくらい当てはまるんですよ!もちろん、たま〜に例外の人もありますけど。」といつも私たちに言うのである。もちろん、私も含めてその周囲の人は「その自信と根拠は一体どこからくるんだぁ!」とツッコミを入れるわけであるが、少なくとも本人は気持ち良いくらい自信満々なのである。とはいえ、私も占いというものは「根拠無しにテキト〜に何かを決めつけることができるという素晴らしいもの」だとも思うので、まぁそれはそれで楽しいわけだ。そんな血液型大好きな新入社員なら可愛いものであるが、それがもう少しエラ〜イ人になるとちょっとばかり大変である。私のとなりの部署の部長なども実はそんな血液型信仰者なのであるが、その部の配属には血液型が参考にされるというオソロしくも確かな真実がある(ホントにホント)。そこの某部長曰く「B型は実験が杜撰だから嫌い。」という実に誠実な理由に基づき、その部はA型人間大集合なのである。というよりも、その部からB型は外されているのだ。恐るべき純血追求型人事手法である。ヒットラーもビックリである。
そんなA型人間大集合の部がある一方で、私が所属している部屋(課)は何故かB型が多い。10人強の中で半数程がB型なのである。どこで読んだのか忘れたが、日本人の血液型はA型35%,B型 25%,AB型 10%,O型 30%位であるらしいから、私の課のB型比率はかなり高い。しかし、もちろんそれは単なる偶然だろう。隣の部がB型を排除しているから私の部屋がB型で溢れているのじゃないか、という恐ろしい想像ができないこともないが、そういうわけでもないだろうと私は信じたい。
しかし、「信じたい」という気持ちだけで物事を決めつけるのは危険この上ない。それは「セーラー服の女子高生はみんな可愛くて純真だと信じたい」という危険さと同じくらいデンジャラスである。何事も、先入観で判断してはイケナイのである。確認することが重要なのだ。そこで、今回は「10人強の中で半数程がB型なんていうのはよくある偶然」だということを血液型分布・配置シミュレーション(超手抜き)でも行って確認してみたいと思うのである。そして、私が所属している部屋(課)にB型が多いのがただの偶然であること、つまりある特定の血液型の人間が集まることが不自然ではないことを確認してみたいのである。
さて、今回の血液型分布・配置シミュレーションのやり方は次の通りだ。
- まずは256人の人間を用意する。
- その256人に対して、A型 35%,B型 25%,AB型 10%,O型 30%位になるようにAB型の抗原(AA,AO,BB,BO,AB,OO型)を配置する。
- その後、遺伝子を移動して血液型を再配置する。
- 近所の人間と子供を作る(遠距離恋愛は考えない)。
- 血液型分布・配置を調べる。
この説明の中で、一言で「遺伝子を移動して、近所の人間と子供を作る」と書いたが、もちろんその現象の中には
- 人が引っ越したり・移動したりしていったり、
- 愛が芽生えて子供がデキたり、愛が芽生えないけどデキちゃったりして子供が出来たり、
まぁ、しかしカマキリのようにエッチのあとにメスがオスを食べちゃう動物もいたりするのだし(実際のところは知らないけど)、この恐怖の「子供が一人出現すると親が一人消えてしまう」システムもそんなに不自然ではないのである、ということにしておこう。というわけで、いつもながらの強引な展開だ。
そんなわけで、行ってみた血液型分布・配置シミュレーションの結果が下の動画である。一マス一マスが一人の人間である。時間毎にどんどん血液型分布・配置が変化していく様子が判ると思う。ちなみに、
赤 = A型、緑 = B型、水色 = AB型、紫 = O型である。
 ファイルサイズがデカイのは直すつもり… |
この結果はカラフルにただチカチカするだけの計算結果ではないのである。このチカチカこそが人生の喜怒哀楽なのだ。そこを是非とも心して眺めてもらいたい、と切望する次第である。
じゃぁ、時間を追ってA型、緑 = B型、青色 = O型、紫 = AB型(色が一部さっきと逆転していることに注意)がどう変化していったかというと下の図のような感じだ。それほど一定ではないことがわかるだろう。それぞれの血液型の比率が逆転したりする下克上な瞬間だってままあるのである。
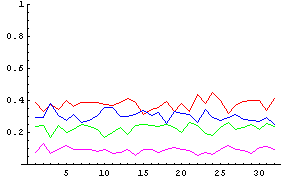 A型、緑 = B型、青色 = O型、紫 = AB型 |
もちろん、これは256人という少ない人数だからこんなに大きく比率が変動するわけである。しかし、今回は「つまりある特定の血液型の人間が集まる」かどうかを調べたいのである。つまり、ある少人数の人間達を考えたときに特定の血液型の比率が多くなることがあるかを調べたいのだから、考える人数は少人数で構わないわけだ。
256人という比較的多い人数を考えた場合ですら、人生のドラマが続く中でそれぞれの血液型比率は結構変化して、それぞれの血液型の比率が逆転したりすることもあるわけだが、じゃぁもっと狭い領域に注目したらどうなるだろうか?例えば、下の瞬間の血液型分布・配置を眺めてみよう。
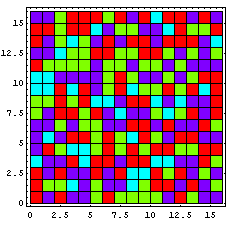 |
おやおや、結構
- A型 = 赤が連続していたり
- B型 = 緑が集まっていたり
- O型 = 紫が多いくせに固まっていたり
- AB型 = 水色が少ないながらも集まっていたり
試しに、先程のシミュレーションである16人(つまり私の部屋(課)の人数位だ)を抽出して調べたときに、A型が一番多かった場合と、一番少なかった場合で、A型の割合だどんなだったかを調べてみたのが次に示すグラフである。ここで、
- 赤 = その瞬間にA型が一番多かったグループにおけるA型の比率
- 青 = その瞬間にA型が一番少なかったグループにおけるA型の比率
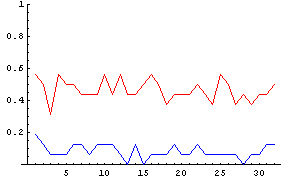 赤 = A型が一番多かったグループにおけるA型の比率 |
なるほど、A型が一番多かったグループではA型の比率が60%を越える時もある。逆にA型が少ないグループでは16人のなかにA型がいない、という状況すらあるのだ。
ということは、私の部屋のB型がほぼ半数という状態だって別に不自然ではなく、それはごく自然なわけだ。もちろん、A型とB型の比率が違うことを考慮しても、全然不自然ではないだろう。ということは、血液型信仰者の某部長による隣の部のB型キライの恐るべき純血追求型人事手法の余波をうけて、私たちの部屋がB型だらけということはなくて、それは単なる偶然だろう、ということがわかるわけだ。
ところで、ここまで書いて「血液型信仰者の某部長」が「ヘンな人」というイメージを持たれてしまうと非常に困る。何故なら、もっと変でなおかつエライ人がイッパイいるのである。(ここでいう「エライ」は関東弁&関西弁のニュアンスだ。つまり、「偉いけど大変な」というニュアンスだ。)血液型信仰者なんてカワイイもんじゃないの、と思えるくらいのスゴサである。だって、ダウジングが超大好きで、奇跡の水が超〜大好きな人だっているのだ。もしかしたら、ダウンジングなんて言葉を知らない人がいるかもしれない。しかし、知らなくて当たり前である。ダウンジングとは下の絵のような棒を持って水脈などの場所捜しをする迷信の中の迷信である。キング・オブ・迷信と言っても良いくらいのアイテムである。
 |
しかも、なんとダウジング&奇跡の水大好き人間が実は某新規材料開発部署の責任者だったりするので、そこらへんは考えると実はかなりコワイものがあるのだが、それはそれ、結構笑える事実(ホントにホント)ので良しということにしておきたい。
2001-05-22[n年前へ]
■今日のオッパイ星人からのメール 
もうご存じかも知れませんが5月23日夜8時からテレビ朝日の「せきらら白書」で、 「せきらら白書 ヘタをすると命取り!!恐怖の“肩こり”一発解消法」と言う特集 が組まれているようです。先ほど、その宣伝を見たところ、なんと、女性の(結 構大きかった?)バストを計りに乗せようとしているところが。(ちらっとしか見て いないので、メールを書いていてだんだん不安になってきたな。)
そうです。「オッパイ星人の力学 - 胸のヤング率編 - (2000.06.29)」 では不明であったために季美子定数を乗していたものが、もしかしたら正しい 値を得られるかもしれないのです。その瞬間、これはメールを出さずにはいら れませんでした。(これじゃ私はオッパイ星人か?)
2003-05-04[n年前へ]
■スカしッ屁の風速ベクトル 
おならの流体力学 放出口外側のパンツ内側編
少し前まで、米軍のステルス戦闘機などの話をニュースで見かけることが多かった。ステルス戦闘機といえば、それはもちろんレーダーには映らないわけで、「音はすれども姿は見えない、まるでアナタは屁のような」戦闘機なのである。これが通常の戦闘機の場合であれば出撃したりするとレーダーに写ってしまって大きな襲来警報のサイレンとともに迎えられたりするわけであるが、ステルス戦闘機の場合にはそんな襲来警報の音もなくいきなり出現するわけで、いわば音を伴わない「スカしッ屁」のようなオソロしい戦闘機なのである。しかし、ステルス戦闘機もオソロしいのだが、スカしッ屁だって十分オソロしい。何しろ、「音のしないおならは臭い」「スカしッ屁は臭い」とよく言われるほどそのに臭いは強烈だとされているのである。スカしッ屁は、ステルス戦闘機のごとくいきなり我々の鼻腔奥深くに達し、そして姿を現した瞬間にはもう我々の体の鼻の奥にその恐怖の毒ガスを充満させていくのである。
ところで、ステルス戦闘機の恐ろしさはともかく「音のしないおならは臭い」というのは本当なのだろうか?当たり前のように口にされる「スカしッ屁は臭い」というセリフであるが、それは何か事実に基づいたものなのだろうか?そんなことはきっと誰しも一回は不思議に思ったことがあるに違いない。そこで、資料などを調べてみると実際にスカしッ屁は臭いという科学的根拠があるらしい。何でも、音がするしないは大抵の場合「おならの量」で決まるらしく、おならの量が多い場合には音がして、おならの量が少ない場合には音がしないというのである。そして、量が多いおならの原因は穀物を食べた時にでんぷんや繊維質が発酵して発生するメタンガスで、それはほとんど臭くないというのである。ところが、量が少ないおならの場合には、そのおならの原因は肉類の蛋白質・脂肪類が発酵して発生するアンモニア・インドールなどで、これが実に臭いというのである。だから、量が多いおならすなわち音が出るおならは臭いけれど、「量が少ないおなら」つまり音のしないスカしッ屁は臭いというのだ。統計的には「臭くないスカしッ屁は気づかれない」から「気づかれるスカしッ屁は必ず臭い」「だからとりたててスカしッ屁が臭いわけではない」という理屈も成り立ちそうなものだが、そんな理屈はさておき「スカしッ屁」の臭いは事実オソロシいものらしい。
「スカしッ屁」の臭いが事実オソロシいとすると、音もなく訪れるそんなオソロシイ兵器から私たちはどのようにして身を守れば良いのだろうか?音もなくいきなり鼻腔に忍び寄ってくる「スカしッ屁」という恐るべき化学兵器からどのようにすれば身を守ることができるのだろうか?そこはもちろん、身を守るためにはまずはその対象をよく知らなければならないのである。敵を知らずして敵に勝つことはできないのである。「スカしッ屁」から身を守るためには、「スカしッ屁」をよく知らなければならないのである。別にそんなことを知りたくもない、という気持ちはもちろんココロの奥底に強く強くあるのだけれど、身を守るためにはそんなことは言っていられないのである。自分のみを守るためには、私たちはおならについて少しばかり考えてみなければイケナイのだ。…というわけで、今回はおなら(毒ガス)が体内から放出(放屁)されたのちに、オナラ放出口近辺で起きている現象を考えてみることにしたい。
今回は、まずはオナラが体内から外に放出された瞬間を考えるために、とりあえず「音のするオナラ」と「スカしッ屁」が「黄門様」から放出されたあとの噴出風速ベクトル(放屁ベクトル)をナヴィエ・ストークス方程式の計算エンジンにNaSt2Dを使って計算してみた。計算領域は放出口の外側、パンツの内側というごく狭い領域である。計算領域の左中央辺りに黄門様が位置しており、計算領域の右側にはパンツがある。また、ここではパンツと言ってもビキニやブリーフのようなピッタリお肌に密着タイプではなく、トランクスのように肌との間に空間が存在するタイプを仮定している。そして、「音のするオナラ」の場合には強く早く小刻みに「ブーッ」っとオナラが放出口から放出され、「スカしッ屁」の場合には「スーッ」と弱~くオナラが黄門様から放出されることにしてみた。下の二つのグラフが、そのようにして計算してみたオナラが出たときの黄門様の外側パンツの内側における「音のするオナラ」と「スカしッ屁」のオナラ噴出風速ベクトルである。音でいうなら、左が「ブーッ」で、右が「スーッ」なのである。
 |  |
もちろん、言うまでもなく上の計算は実に大雑把で簡易的なものだが、「音のするオナラ」の場合には、おならの風速ベクトルの方向が刻々変わり、またその大きさも大きいことから、放出口外側ですぐに急速に拡散してしまうことが予想される。すなわち、毒ガス濃度がパンツ内ですぐに薄まり、おならガスの危険度が低下していることが判る。黄門様の外側パンツの内側でおならガスが急速に拡がっているようすが目に浮かぶようである。絶対に、目に浮かべたいとは思わないのだがこのグラフを見るとそんな様子がまぶたの裏にまざまざと浮かんでしまうのである。
それに対し、「スカしッ屁」は「スー」っと滑らかに出るがために毒ガスが拡散せず、放出口を出た後も毒ガスの危険濃度を保ったまま「まとまったガス雲」として戦隊飛行を続けていくことが予感される結果なのである。「スカしッ屁」はその毒ガス成分だけでなく、そのガス拡散度合いも考えてみる価値もあるかも知れない(考えたくないが)、とも思わせるのである。
というわけで、今回は何とも中途半端な計算をしただけで、オナラの風速ベクトルを予想しそのオナラの運命に考えを巡らせてみたのであるが、その中途半端さには実は理由がある。何しろ、これまでスクール水着、疑似オッパイ、山本式エアコンなどさまざまな物体に対する流体計算をしてきたが、今回の黄門様近くのスカしッ屁の風速ベクトル計算ほど何ともやる気がおきず、気が乗らず、頭の中で計算対象を想像したくないものも初めてなのである。対象物を強く心の中でイメージできなければ、まともな予想などもできないわけであるが、どうにもパンツの中のオナラをイメージしたくなかったのである。そのせいで、どうにも中途半端な結果になってしまったのである。
あぁ、こんなことではオナラから身を守ることができないぞ、おならを心の中で強くイメージしなければイケナイぞ、と強く自分を戒め、続編へ向けてがんばらなければと思う今日この頃なのである。が、しかしまた、おならを心の中で強くイメージするのと、オナラから身を守るのであればどっちが重要か少し悩んでしまい、続編もちょっと…と思ったりもする今日この頃なのである。
2003-06-17[n年前へ]
■アルキメデスのパンチラの式 
「スカート円錐」の明るさを探れ
「スカート円錐」の明るさを探れ
以前、「ミニスカートの幾何学」として、女子高生の間などで流行っていたミニスカートの丈の短さの限界について考えてみたことがある。階段を上ろうとしているミニスカートを履いた女性(別に男性でも構わないが…)の下着が見えてしまうかあるいは見えないのかを、女性達が履くミニスカートの丈の長さから考察をしてみたのであった。その「ミニスカートの幾何学」の考察をした結果、ミニスカートの丈がちょうど32cmの時に、ミニスカートで下着が隠されはじめる境界線がちょうど階段と平行になる、ということが判ったのである。そして「下着が隠されはじめる境界線がちょうど階段と平行になる」結果、ミニスカートの丈が32cmより短いと下着が階段下を上る人達から見えてしまうようになり、逆にミニスカートが32cm以上の丈であればスカートの中の下着はなんと幸か不幸か見えることはないのだ、ということが判ったのである。ミニスカートをはいた女子高生が急な駅の階段なんかを上るときでも、ミニスカートの丈が32cm以上であれば、パンチラの恐怖に怯える必要はないということが判ったのであった。
ところで、ミニスカートの中が見えてしまいそうになる場所というのは、必ずしも急な階段だけではないらしい。最近の東京の有名スポットなどでは、「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかがたくさんあったりするというのである。そして、そんな場所では、真上にいる「スカートを履いた女性」を急角度で仰ぎ見ることができて、スカートの中の下着がチラリと見えてしまうことがあるというのである。
しかし、である。角度的にスカートの中の下着が見えるからといって、果たして本当に下着が見えるものなのだろうか?角度的には見えるはずでも、実際には人間の目には見えないことだってあるのではないだろうか。なぜなら、スカートが「私たちの視線から下着が見えるのを遮っている」のと同じように、スカートは「照明の光が下着にあたるのをも遮っている」のである。スカートの中というのはスカートに光が遮られて(たぶん)かなり暗いハズなのである。いや、実際に覗いてみた経験があるわけでは決してないので自信を持って「ハズ」と断言することはできないのだけれど、スカートの中が明るいわけはないと思うのである。もし、スカートの中が明るくなければ、仮にその中身を覗くことはできても結局暗くて何も見えないわけで、「スカートの中が(見えるくらいに)十分に明るいかどうか」が肝心だと思うのである。そこで、今回は「下着が角度的に見通せる条件」ではなくて、「スカートの中の下着が十分明るく見える条件」を考えてみたい。
まずは、スカートをはいた女性を下の図のように簡単に示してみよう。スカートを下向きに開いた円錐として考えてみる。もちろん、スカートの中の下着はこの円錐の頂点に位置するわけだ。そして、スカートが広がる角度をΘとでもしてみることにしよう。その時、円錐の頂点にはどれだけの光が当たるものだろうか?
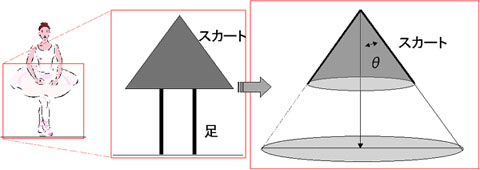 |
もちろん、円錐状のスカートが上からの光は遮っているわけだから、スカートの中の下着を照らす光というのは、下の床からの反射光だけである。つまりは、上の図で、「色を付けた部分の床」からの反射光のみが下着にまでたどり着き、それ以外の床からの反射光はスカートに遮られて、スカートの中を照らすことはない。ということは、「スカートの中はどれくらい明るいか?」という疑問を考えることは、それは「色を付けた部分の床からスカートの中の下着にまでたどり着く光がどれだけあるか?」ということを考えることと同じなのである。
そしてまた、床上での光の反射に方向性が無く、光が完全に等方的に周囲に拡散するとするならば、円錐の中心(つまりはスカートの中の下着部分だ)にあたる光の量は、下の左図の色を付けた部分球の面積に比例する。つまり、「スカートの中の明るさ」は「スカートの広がり角」で決められる「部分球」の面積に比例するのである。
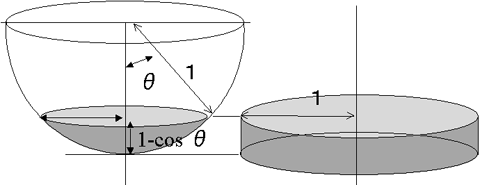 |
つまり、角度Θで広がるスカートの中が「どれくらい明るいか?」という疑問は、「下図で色を付けた部分球の面積はどのくらいか?」という問題に変わるわけである。「半球全体の面積に対して、スカートの広がりで決められる部分球の面積はどのくらいの割合か?」ということの答えが、それすなわち「スカートの中の明るさ」を決めているのである。
ところで、アルキメデスが発見したように、球(もしくはその一部)の面積はその球に外接する円筒の面積に等しい。つまり、上の図の左で色を付けた部分の面積というのは、右に示したような(色を付けた)円筒の面積に等しいわけだ。ということは、右の円筒部分の面積は
円筒の面積 = 2 π (1-cosΘ)であって、左の半球の面積が(直径=1とすると)2πだから、円錐状のスカートの中の明るさは、スカートの広がる角度をΘとするならば、「スカートの中の明るさ」は
という実に簡単な式で表されることになる。アルキメデスも、まさか自分の球と円筒の表面積に関する発見が「スカートの中の明るさを示す式(ここでは仮に『パンチラの式』とでも呼ぶことにする)」を導くために使われるとは想像だにしなかっただろうと思うが、とにかくアルキメデスのおかげで私たちはスカートの中の明るさを知ることができるのである。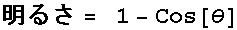
試しに、このくアルキメデスの『パンチラの式』を使って、スカートの広がり角度Θに対して、スカートの中の明るさがどのように変化するかを計算してみると、その結果は下のグラフのようになる。このグラフは、横軸が「スカートの広がる角度」で、縦軸が「スカートの中の明るさ」を示している。周囲の「照明に照らされている床」の明るさを1とした時の「スカートの中の明るさ」を示しているのである。
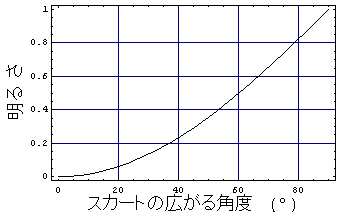 |
基本的にはスカートが広がるにつれて「スカートの中の明るさ」は明るくなるわけであるが、このグラフを眺めてみると、スカートの広がる角度が20°を超えるあたりから次第にスカートの中が明るくなることが判るだろう。例えば、スカートの広がる角度が30°の時には、スカートの中は「床の明るさの10%程度の明るさ」しかないが、スカートの広がる角度が60°にまで広がれば、スカートの中は「床の明るさの半分程度の明るさ」になる、ということが判るわけだ。
ところで、人間の目というものは「見るものの明るさ」に合わせて順応する。例えば、暗いものを見るときには目の感度は自動的に上がる。だから、スカートの中がほのかでも明るかったならば(例えば床の明るさの5%程度にでも明るければ)、自動的にその明るさに目が順応してスカートの中が見えてしまうかと思いきやそうはいかない(ハズだ)。なぜなら、人間の目は明るいものを見る時には、目の感度が逆に自動的に低下してしまうからである。スカートの中以外の明るい場所(例えば照明や、照明に照らされた明るい壁)だって、自動的に視界の中に入ってくるわけで、目の感度はそういう明るい部分に自動的に合ってしまうハズなのである。
例えば、下の画像は周りの明るさに対して、
- 5%の明るさ
- 10%の明るさ
- 20%の明るさ
| 5 % | 10 % | 20 % |
ということは、先のグラフで「スカートの中の明るさ」が10%を超えていないと、つまりは周囲にある明るい床(や照明や壁)などの明るさの10%を超えているくらいでないと、スカートの中が仮に幾何学配置的に見える条件であったとしても、実際には目の感度的にその中のようすを判別することができないに違いないのである。その場合、おそらく明るい床や壁の明るさに目の感度が合ってしまい、ほの暗いはずのスカートの中は真っ暗にしか見えず、幸か不幸かスカートの中身は識別することができないハズなのだ。
というわけで、先ほどのグラフに「識別できる明るさか否か」を書き入れてみると、次のグラフのようになる。
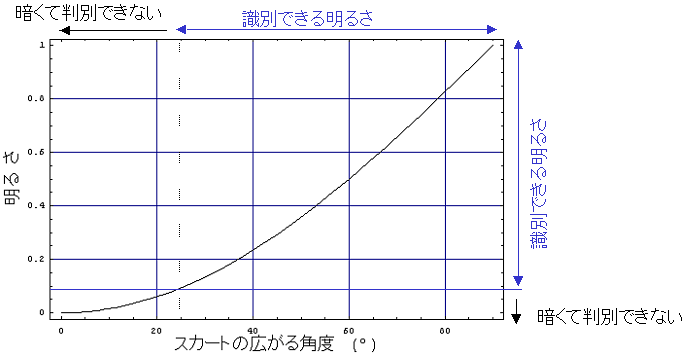 |
つまり、スカートの広がる角度が25-30°を超えていないと、スカートの中身は周囲の床や壁の明るさに比べて相対的に暗すぎて人間の目ではおそらく見ることができないのだ。
例えば、スカートの広がる角度が30°以下に制限されるようなタイトスカートを穿いて、明るい壁や照明などが視界にどうしても入ってしまうような場所にたたずんでいる限りは、もし仮にスカートの中を覗かれたとしてもスカートの中は(人間の目からすると)真っ暗で何も見えないわけで、スカートの中身を見られたりするような被害にあうことはまずないだろう、ということが先のアルキメデスの『パンチラの式』から判るわけなのである。「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかであったとしても、背後に明るく輝くものがある限りには、見る人の目を眩ませることができて、スカートの中身は安全なわけである。
ところが逆に、床が白かったりして明るいクセ(つまり下からの照明が強いクセ)に、周りに明るい壁や照明が何故かあまりないような場所がもしあったとして、もしそんな場所で(下から)スカートの中を覗かれたりしてしまうと、(下から覗く人の視界に入る)周囲の明るさに比べてスカートの中が十分明るく見えるせいで、しっかりとパンツの模様をチェックされてしまうということになるだろう、ということも予想することができてしまうのである。だから、そんな場所をもしも短いスカートをはいて歩かなければならないような場合には、例えば何かの「ピッカピッカ輝く光りモノ」でも身につけて、その光りモノの明るさを「スカートの中身をのぞこうとするスナイパー」の視界に入れて、彼らの目を眩ませてしまえば良いだろう、というアルキメデスの知恵さえ授けてくれるのだ。
ところで、今回は「スカートの中の明るさを示す=パンチラの式」を考えてみたわけであるが、この式は考えるまでもなく実にアブナイ式である。パンチラの被害防止に役に立ちそうな気もするし(全然役に立たないような気もするが)、逆に単なる「パンチラの科学」になってしまっているような気もしてしまう。「スカートの中身をのぞこうとするスナイパー」の魔の手から逃げるためのバイブルになるような気もするし、「スナイパー」のための手引き書になってしまいそうな気もする。ギリシャ神話で、あらゆる災厄が入っていたという箱がパンドラの箱だったけれど、このパンチラの式だって案外そんなパンドラの箱のような、色んな災厄の元になってしまうものかもしれないのである。しかも、パンドラの箱の場合には最後に箱の中に『希望』が残っていたわけでまだ良い(?)のである。しかし、アルキメデスの『パンチラの式』の場合には「スカートの中にだっては『希望』が入っているのだぁ」などと口に出したりしたら単に変態扱いされてしまうだけなわけで、そこはパンドラの箱よりもずっとたちが悪いのである。つまりは、科学もアルキメデスの『パンチラの式』も使う人次第なのである。