1999-11-13[n年前へ]
■やっぱり、ウニが好き ! 
Dr.フラーはウニの夢を見るか?
私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。と、始めると
の間違いと思われるかもしれない。しかし、それは違う。今回は、ウニとドームハウスの共通点について、考えてみたい。ただ、かなりビールが脳みそにしみているせいか、少しドンデモ話になるかもしれない。そこは、「ビックエッグの力学」と共通である。 私の中では、野球観戦と言えば、ビールだ。野球にはビールが良く似合う。そして、今現在も目の前にはビールがある。そして、寿司がある。といっても、スーパーで買った安物である。二つ合わせても1000円にしかならない。
 |  |
安物といっても、私の住んでいるのが港町だから安い、ということもある。何しろ、ほとんどのスーパーの魚売り場でイルカの肉なども置いてあるのだ。嘘ではない。ホントにホントである。私も、引っ越してきた当時はビックリしたが、本当である。アメリカの動物愛護団体が見たらびっくりの風景だろう。「イルカと人間はお友達」と言ってる人には見せられない風景だ。
あまりおいしそうではないので、私はまだ実際に味わってはいない。しかし、地元の人の中には「よく食べる」と言う人もいる。いつか、挑戦してみたい。
さて、上の写真で共通しているのはウニである。ウニと言えば、こんな姿をしている。
 |
「海栗」と書いてウニと読むことが実に納得できる姿である。しかし、内面はもう少し違う。実は、ウニはドームにそっくりである。前回考えたドーム球場ではないが、ウニは実はドーム構造をしているのだ。「そんなことは当たり前じゃないか」と言う人もいるだろう。しかし、私はつい最近までそれを知らなかった。そもそも、骨があるとすら思っていなかったのである。
もしかしたら、私のようにウニの内面を知らない人もいるかもしれない(そんな人はいない、という声も聞こえそうだが)。そこで、ウニの骨の写真を示してみる。下に示すのが、色々なウニの骨だ。
 実物はとてもきれい。日本古来の木工細工のような穴がとてもきれいである。 |
これは少し前に、宇宙科学研究所の黒谷氏の実験室を見学(ただ邪魔しただけという気もするのであるが)する機会があり、そのとき頂いたものである。最初に見たときは、「目からウロコ」であった。まさか、あの針の山の下にこんな頑丈な殻が存在しているとは、思わなかった。
写真ではわからないかもしれないが、骨には小さな穴が極めて規則的に開いている。それが、日本古来のとても出来がいい木工細工のようである。光に透かしてみると、うっとりするようなきれいさである。内部に強い光源でもおけば、プラネタリウムやミラーボールみたいに細い光線を放射する、きれいなアクセサリーができそうだ。
ところで、「何故、宇宙科学研究所の実験室にウニが?」と思われる方は、WEBで検索でもかけてみると良いかもしれない。「宇宙生物学」という面白い実験分野があるものだ。
例えば、無重力の中で生物がどのような挙動を示すか、などの研究をしたりするらしい。飛行機にのってそういう実験を繰り返すわけである。遊園地のフリーファールやバンジージャンプ、そして、ジェットコースターでさえ、駄目な私には地獄のような研究分野である。
さて、上の、ウニの骨の姿はまさにドームそのもの、とは思えないだろうか? そう、似ているのだ。 そっくりなのだ。試しに、このドームなどを見れば納得できるだろう。
 |
これは、富士山頂の厳しい環境を耐えるために、極めて安定なドーム構造が用いられているのだ。三角形のパネルが組み合わさるドームハウスは極めて頑丈である。ウニも、同じように頑丈なドーム構造の骨格を持っているのである。レーダードームは富士山頂で頑張っているが、宇宙科学研究所のウニは色々なところへ連れて行かれて、厳しい実験に耐えているのである。
こういった、ドームと言えば、R.バックミンスター・フラー博士のドーム理論だろう。フラー博士とドームハウスのスケッチ図を示してみる。
|
よく、環境適応性の高さを謳うことの多いドームハウスであるが、もしかしたら、ウニがその祖先であるかもしれない。もしかしたら、フラー博士は「海の中でじっとたたずむウニの夢を見て」ドームハウスを思いついたのかもしれない。
アメリカ人であるフラー博士がウニを食べたとは思えない、という人も多いだろう。それは確かにその通りである。しかし、フラー博士はかなりの変人である。変人ならば、ウニを食べまくっていたとしても、おかしくはない。
普段は「何を馬鹿な発想だ」と思うことだろう。しかし、ドーム球場の野球を見ながら、脳みそがビールとウニで満たされてしまうと、「そうだ、フラー博士はウニが大好きなのだ!そうに違いない!」と確信してしまうのだ。
仮に、フラー博士がウニに影響されていないとしても、ウニはフラー博士がドーム理論を考えるずっと太古の昔から、ドーム構造をしていたのである。ならば、「元祖はやはりウニなのだ!」と言ってしまって良いだろう。太古から厳しい環境を耐えつづけてきたウニは、今や宇宙へ飛び出し、さらに厳しい環境の中で活躍しているのである。
2000-01-31[n年前へ]
■落ちゆくエレベーターの中…で悩みます? 
無重力の理想と現実(仮)
今日もまた「ちゃろん日記(仮)」を読みに行くと、何とも面白い話があった。
である。この「ちゃろん日記(仮)」は「疑問とそこに隠れている真実を見つけだす感覚」に満ち溢れている、と私は思うのである。面白すぎである。さて、今回の話は、エンパイアステートビルでエレベーターが落ちたっていうけど、落ちていくエレベーターの中の人は
- 床に張り付く
- 天井に張り付く
- 宙に浮かぶ
「ほんとう〜にそうか? ほんとう〜にそうか?」
こういういかにも教科書に載っていそうな話には、時として落とし穴がある。教科書に書いてあるのは理想的で単純化した場合の結果である。それを鵜呑みにすると間違えてしまうことになる。極端に言えば、教科書に書いてあるような理想的な状態はほとんど存在しないので、教科書に書いてあるような現象はそうそう再現しない、ということになる。
ピサの斜塔から「落下の実験」を行ったのはガリレオ・ガリレイであると思っていると間違いである、というのは少し違う例になってしまうか。
久しぶりに思い出したが、私の所属していた研究室では重力測定は大きな柱であった。そして、確か大学院の入試問題の内の一題は、まさに
「落ちていくエレベーターの中の人達に働く力を精密に論ぜよ」であった(簡単に大雑把に言えば)。私はちゃんとこの問題を解けた覚えがない。いや、はっきり言えばずいぶん悩んだ覚えしかない。ってことはいまいち解けなかったのだろう。なので、「落ちていくエレベーターの中の人達は無重力状態である」と聞くと、「ほんとう〜にそうか? ほんとう〜にそうか?」と歌いたくなる。
研究室関連では、絶対重力測定を行う研究をする人達もいたわけである。絶対重力(加速度)測定は自由落下する物体の運動を測定して、重力加速度を測定するわけであるが、そう簡単に物体は自由落下してくれないのである。簡単な実験で物体を自由落下させて重力加速度を測定してみるとわかるが、大雑把な実験(自分の家ですぐできる程度の)では一桁ちょいの精度しか出ない。一桁ちょいの精度しかでないということは、(例えば)体重が10%弱程度になったように感じるかもしれないが、それは無重力ではない。体重が60kgの人であれば、6kgも感じてしまうのである。(雑な話だが。)
空気中を落ちてくる雨だってそうだ。もし、雨が自由落下を続けていたらものすごいスピードになって、雨に打たれるのは命がけになってしまう。しかし、実際にはそんなことはない。空気抵抗で速度は飽和してしまい、自由落下状態ではないからである。
さて、本題である。果たして、
例えば、
- 若井研究室の研究概要
- http://mech.gifu-u.ac.jp/~wakailab/research/Basic/base_h.html
北海道の上砂川町にある施設(JAMIC)で、490m落下させることにより、10秒の無重量環境が得られます。落下中は空気抵抗を受けるので、落下カプセルを二重構造にし、空気抵抗を無視できるように工夫してあります。と、記述されているように、実際には工夫をこらさなければ無重力状態は実現できないのである。絶対重力系などでも空気抵抗を無視するために、投げ上げて往復運動を測定するなどの工夫がいるのである。
と、言葉だけで書いてもしょうがないので、適当な計算でもしてみる。いや、もちろん、実験をするのが良いわけであるが、面倒だし…
まずはエレベーターには、
- 何の抵抗も働かない
- 空気抵抗とワイヤーの抵抗が働く
そして、エレベーターの中の人には空気抵抗は働かないとした。エレベーターの中の空気と人の速度差はほとんどないからである。また、エレベーターは人よりもはるかに重く、人の重さはエレベーターの運動に何の影響も及ぼさないと近似した。
その計算の結果を以下に示す。これが落ちていくエレベーターの軌跡である。抵抗のない場合が(赤)で抵抗のある場合が(青)である。エレベーターが落ち始めてから30秒後までの軌跡である。
 |
理想的な場合(赤)に比べて、抵抗のある場合(青)の落ち具合が鈍っているのがわかると思う。それでは、もっと時間が経った場合はどうだろうか?それを次に示す。エレベーターが落ち始めて300秒後までの軌跡である。つまり、五分間もこのエレベーターは落ち続けているのである。落ちた距離は理想的な場合で40kmの深さに達している。すごいエレベーターである。こんなに落ち続けていると、すでに重力加速度が一定とは言っていられなくなる。
 |
ここまでくると、抵抗のない場合(赤)と抵抗のある場合(青)では全然違う軌跡になっている。抵抗のない場合(赤)では放物線そのものであるが、抵抗のある場合(青)では一定の速度になっている。
それでは、エレベーターがこのような状態になった時の、エレベーターの中の人に働く加速度(と実際の加速度の差分)を示してみる。これを見れば、落ちていくエレベーターの中の人が無重力状態であるかどうかがわかる。まずは、300秒後までの変化を見てみる。
 |
理想的な場合(赤)はずっとゼロすなわち無重力状態であるが、抵抗のある場合(青)は無重力状態は最初だけで、50秒後位には通常の状態に戻ってしまっている。最初の部分をもう少し拡大してみる。次に示すのは、3秒後までの落ちていくエレベーターの中の人に働く重力加速度(と実際の加速度の差分)である。
 |
これを見ると、あっという間に人は無重力状態ではなくなっているのがわかると思う。
というわけで、先の三つの選択肢、
- 床に張り付く
- 天井に張り付く
- 宙に浮かぶ
先日みたニュースのエレベーター落下実験の中で、中にいた男性リポーターが、落下しながら「ひぃ?」とアオ向けになった状態で床にハリ付いていたからなのです。という実際の現象が正しいのである(いや、もちろん状況はかなり異なるが)。「頭の中だけ」で考えたことというのは大抵の場合間違ってしまう。(もちろん、今回の「できるかな?」の話もその例外ではない)
そして、その後に、
ありはきっと、速度がそこまで充分でなかったのと、もしやのトキのために、男性リポーターに安全な姿勢をとらせていたタメだと思われます。とあるが、実際問題として「速度がそこまで充分」になることは未来永劫ないわけである。だから、(私の中では)エレベーターの中の男性リポーター氏は床から浮かぶことはないのである。
こういうのは、結局考える人の数だけ答えがあるのだと思う。もし、その内のどれが真実に一番近いかどうか知りたければ、実験すれば良いだけの話だし。
2001-01-13[n年前へ]
■オッパイ星人の力学 第四回 
バスト曲線方程式 編
先日、父から封書が届いた。二十一世紀にもなったというのに、e-mailでもなくて封書が届いたのである。これは、やはりアレだろうか。いい年にもなってるのに、クダラナイWEBサイトを立てているデキの悪い息子を厳しく叱るためだろうか?しかも、そのクダラナイWEBサイト(しかも、有害公式認定サイト)の名前が自分の名前(hirax)だったりするからだろうか?それとも、「本が出たなら送れ」とは言われても実は送りたくなかった「あの本」を、少し前に父に送ってしまったからだろうか?いや、それとも…そんなこんなでドキドキしながら封筒を開けると、記事のコピーが二つ入っていた。他には何も入っていないのである。一体これは何の記事だろう?と思いながらそのコピーを眺めてみた。すると、まずひとつは去年の12月25日付けの毎日新聞の科学欄である。二十一世紀を専門家達が予想した記事の横に「究める」というコーナーがあって、そこに「女性の胸と男性の好みの進化的関係は?」というインタビュー記事があった。そして、その記事が蛍光ペンでマーキングしてあったのである。
これは一体、どういうことなのだ?と頭の中がグルグル&複雑な気持ちになりながら、とりあえずその記事を読んでみた。すると、この記事がとても面白い。インタビュー中の
ヒトは異性をどう選ぶのか?そんな疑問から女性のバストと弾性の好みに進化的関係があるかを研究している。という東大大学院の東海林さんの語りもとても面白いし、バストサイズを5段階に変えた女性の合成写真を使い、男子学生300人にアンケートしたという実験とか、巨乳好きの性格が父から受け継いだものであるかを調べるために、父子間で性的好みが伝達されるかを調べる、などの話もとても面白い。最高である。(中略)小さいバストほど魅力的だと母に教えられて育った。しかし、大きいバストが好きな男性がいることに気付いて驚き、「なぜ」と考えたのが研究のきっかけだった。(中略)「大きいバストが本当に普遍的に好まれるかを知りたい。控えめなバストが淘汰されてしまうとは考えたくないから」と話す。
そして、父からの封筒に入っていたもう一つの記事は宇宙科学研究所の新聞の中の宇宙基地利用研究センターの黒谷氏の「Anti-Gravity」というエッセイだった。なんでも、Anti-Gravityという化粧品があって、
それは顔の皮膚のコラーゲンに皮膚がたるまないようにするというものらしい。顔の皮膚にハリをあたえて、顔のたるみを防ぐのである。顔の皮膚のたるみ元をたどれば重力のせいだから、「anti-gravity= 無重力」化粧品ということになるわけだ。じゃぁ、このAnti-Gravityを体中に塗れば、バストやヒップが垂れるという女性の悩みもなくなるのではないか、と「無重力における生物の専門家」である黒谷氏は書いていて、参考文献に本サイトが挙げられていたのである。
うむむ、世の中には巨乳の科学について進化論的に研究している人がいたり、オッパイの力学について考え(てみたりもす)る無重力生活の専門家もいるのだ。これはマズイ。油断している場合ではない。私もオッパイ星人研究をもっと真剣にしなければならない。父はきっと私に「研究の厳しさ」を教えようとしたに違いないのである。私の父はこれまでの「オッパイ星人の力学」を読んで、美味しんぼの海原雄山風に「うわあっはっ、こんなものでオッパイ星人の力学だとは笑止千万!」位のことを言ったに違いないのである。
しかし、それだけではない。「二十一世紀、小さいバスト、大きいバスト、無重力、皮膚、オッパイのたれ」というヒントを与えてくれたのである。ここまでされて何かを書かなくて何としよう。オッパイ星人研究の手は一瞬たりとも休めてはならぬのである。そこで今回は「皮膚のハリ」や「重力」を気にしながら、「オッパイのたるみ・形状」について考えてみることにした。
さて、一体バストの形状というものはどうなっているのだろう?これまでの「オッパイ星人の力学」では
- 半球モデル
- 円錐モデル
そしてもちろん、このモデルに対して不満を持つのは私だけではなくて「これらのモデルには私は納得できません。」というメールがたくさん送られてきた。それどころか、「本当のオッパイをあなたは知らないのではないですか?」という実に失礼?なメールさえ送られて来ていたのである。「それでは、参考までに本当のオッパイの資料でも送って頂けないでしょうか?」とは私は大人なので返事をしなかったが、ちゃんとしたモデルを作らないことにはこれからもそんなメールがまだまだ来るに違いないのだ。
というわけで、今回は新しいバストの形状モデルを提唱してみたい。それは「バストの内部は液体に満ちていて、その液体を外側の皮膚が支える」という
- 水風船バストモデル
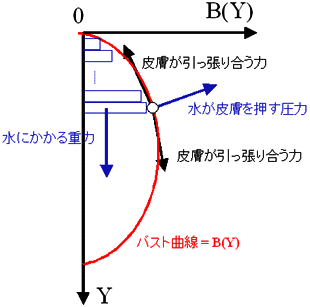
こんなモデルに基づいて、バストの形状を計算するにはどのように考えれば良いだろうか?次の図が「水風船バストモデル」における内部の水と各皮膚部分にかかる力を示してみたものである。これはバストの断面をを鉛直方向に示しており、左の黒い鉛直線が胸板であり、赤い線がバストの形状を示すバスト曲線である。(ちなみに、今回はバストを二次元の断面でのみ考えている。)
赤い線がバストの形状を示すバスト曲線
|
「水風船バストモデル」における内部の水には重力がかかり、バストの下の方にいくほど圧力がかかっている。そして、皮膚に面している内部の水はその圧力を皮膚に伝える。そして、皮膚はその圧力で変形しながら水で満ちたバストを支えるのである。この時、バストの形状= 皮膚の形状を示すバスト曲線はどんな条件を満たしているだろうか?
ここで、胸板にそって下向きにY軸をとり、バスト曲線をB(Y)で表すことにしよう。上の図をよく眺めるとわかると思うのだが、バストの形状= 皮膚の形状を示すバスト曲線をB(y)とすると、バスト曲線B(y)は実はこんな方程式を満たす。
 |
まぁ、ここでは簡単のために、係数を省略していたり、バストが本当に垂れてしまうような状況は考えていなかったりするので、ごく簡易的なバスト曲線方程式だと思って欲しい。大雑把に係数などを無視して、言葉で言ってしまえば、バスト曲線の傾きの変化はその点より上に位置するバストの重量に等しい、という感じである。自由境界におけるLaplaceの関係でも連想して頂ければわかりやすいだろうか?とにかく、この条件と適当な境界条件さえ入れてやれば、「水風船バストモデル」におけるバスト曲線B(y)は計算することができるのである。
さて、このバスト曲線方程式を一般化したり、係数をちゃんと計算したり、三次元に拡張したりということはまたいつか行うことにして、まずは適当にこのバスト曲線方程式を数値的に解いてみた。それが、例えば、次の図である。これが、「水風船バストモデル」のバストの形状の一例だ。
赤:すごくハリのあるヤングな皮膚の場合 |
この図の中でバスト形状のプロットが三種類あるのは「皮膚のハリ = 皮膚のヤング率」として三種類の値を使ってみたからだ。以前
の中でそう、もうお判りのはずだ。 「バストに関するヤング率」はまさにヤング率(Young率)なのである。実は年齢に比例する係数だったのだと書いたが、あれと同じである。今回は、年齢で変わっていくバストの皮膚のハリを「バストの皮膚のヤング率」とおいてみたのである。そういうわけで、皮膚のハリ= 皮膚のヤング率によってバストの形状は異なるわけだが、まずは眺めてみてもらいたい。以前のどうみても不自然な「半球バストモデル」等に較べて、ずっとましになっているとは思わないだろうか?特に、藍色・マゼンダのプロットなどかなり自然な形状になっていると思うのである。感受性の豊かなオッパイ星人であれば、必ずしやググッとくるハズである。
さすがに、メチャクチャ皮膚のハリがある赤色のプロットなどは松坂大輔もビックリの「超ロケット乳」になってしまっているが(といっても、この図のアスペクト比に意味はないんだけど)、今や時代は二十一世紀、宇宙へロケットで飛び出す時代だと思えば、こんな「超ロケット乳」を眺めるのもそれまた一興ではないだろうか。ぜひこの「超ロケット乳」には宇宙へ飛び出してもらいたいものである。
もちろん、世の中には「大きいことは良いことだ」という巨乳大好きオッパイ星人達もいるわけで、そんな人達のためにもう少し「大きいバスト」の場合で計算してみたものと並べて比較してみたのが次の図である。
 |
個人の好みもあると思うが、けっこう自然な「巨乳形状」が再現できている。ちなみに、今回使用した簡易的なバスト曲線方程式ではすごく巨乳だったり、皮膚のハリが無さ過ぎてあまりにバストが垂れている場合の計算はできない。簡単に言えば、Yに対してバスト曲線B(Y)が一対一対応しないためである。が、それゆえに巨乳と言っても美乳の範囲のみ考えることができるのである。
また、この「小さいバスト」の場合と「大きいバスト」の場合の比較から、「巨乳は垂れるのよっ!だから、小さい方が良いのっ!」という世の小振りなバストの女性がよく言うセリフの妥当性も確認してみたいところではなるが、そういうことは何か危険なことであるような気もしてきたので、今回は止めておきたい。
ところで、今回の話はAnti-Gravityから話が始まっているわけだが、ちなみに「水風船バストモデル」は無重力下ではどのような形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。つまり、「半球バストモデル」は「水風船バストモデル」の重力を無視した特殊な場合であり、逆に言えば「水風船バストモデル」は「半球バストモデル」にバスト内部での重力の影響を加えて一般化したものだったのである。
今回は、とりあえず新たに「水風船バストモデル」を提唱し、そのモデルにおけるバスト曲線B(y)を解くための簡易的な方程式を考察し、それを数値的に試しに解いてみた。次回は今回行った考察を用いながら、少し違うアプローチで「オッパイ星人の力学」を考えてみたいと思う。
さて、今回の話のきっかけともなった黒谷氏らの書いた本「星と生き物たちの宇宙」は原稿のごく初期の段階で実は読ませてもらっていた。その時感想を聞かれたときは、この本はメールのやりとりで構成されているので、「なるべく著者達の私的な部分を消さないままにしておいた方が面白いんじゃないか」なんて適当なことを言っていたのだった。その著者達が書いたこの本のあとがきの言葉を最後に引用して、これからの「オッパイ星人の科学」への「戒め」と「言い訳」としておきたい、と思うのだった…
科学は応用を通じて実生活に関わり、知的追求というこころの喜びにも関わる二面を持っています...多くの人に、こころを喜ばせる科学を楽しんでもらいたいですね。 H.Hirax, A.Kurotani
2001-01-16[n年前へ]
■バスト曲線その2 今日書いたメール。 
あの方程式は
>液体の圧力は水平方向ではなく表面の法線の方向に働くので
このとおり、表面の法線方向の関係に直されていますし、それが「自由境界におけるLaplace の関係」そのものですよね。
>というのは液体の圧力は水平方向ではなく表面の法線の方向に働くので、
>ヤング率が大きくなる程半球に近付くはずです。
単に液体の自由境界を計算するときと同じように解けば、あの文章の末尾に
>ちなみに「水風船バストモデル」は無重力下ではどのような
>形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。
と書いたように仰るとおり半球に近づくように一見思えます。
ここで無重力下というのは、皮膚の張力が重力に較べて十分大きい、ということなわけで「ヤング率が大きくなる」のと同じなわけです。
ところがところが、です。
「あの方程式を解くときの境界条件は胸板側の長さ・バストの体積を先に決めています。」
また、「あの座標軸の下で方程式を解く」ために、あの方程式はY,B(Y)の一対一の対応を必要としています。それが、「バストが本当に垂れてしまうような状況は考えていなかったりするので」という前提ですね。
この二つの境界条件・前提の下で、「ヤング率が大きくなる程半球に近付くはず」が本当に正しいかどうか、考えてみては如何でしょうか?
この二つの条件を除外しようとすると、方程式を作って解くのがとたんにメンドーになります。
というわけで、一般化されたバスト方程式をぜひ作って解いてみて下さい。
2003-09-06[n年前へ]
■Elasticity Simulatorで眺める「オッパイ星人のヤング率」 
どうせなら面白く物理を眺めれば、きっと中高生(大学生も?)科学を好きになるだろうということで、どうせならElasticity Simulatorで「オッパイのヤング率」を眺めてみることにしよう。
まずは、このJava Appletから 1."shape"から"disk"を選択する
2.真ん中の点を全て右クリックして、固定点(大きい丸)に変更する
3."triangular mesh"にチェックを入れる
4."gravity"にチェックを入れる
という順番の作業をする。すると、こんな画面になる。

固定点を作成したことでこのモデルは左右対称になったわけで、(例えば)左半分を無視して眺めてみることができる。つまり、こんな風に「半球状に」眺めることができる。


ハイ、判りましたでしょうか?つまり、このElasticity Simulatorは「オッパイ・シミュレータ」に大変身するわけです。"material"を変えて、ヤング率を変えることで「堅いオッパイ」「柔らかいオッパイ」、「ヤングなオッパイ」「アダルトなオッパイ」などさまざまな物理実験をすることができるようになります。もちろん、無重力条件下とか動的特性なども眺めることができるのです。
これで、きっと物理大好きな中高生ができあがり、です。少し動機がヘンかもしれませんが、とりあえず弾性体物理学(それともオッパイ)が大好きになるハズです。というわけで、こんな「物理講座」に対する中高生を持つPTAのご意見などを少しばかり聴いてみたいところですねー。感謝の声か、非難の声か、さてさてどちらでしょうねぇ。