hirax.net::Keywords::「面積」のブログ

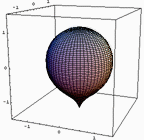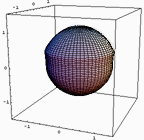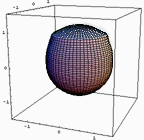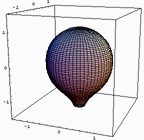
■バスト曲線その2 今日書いたメール。　

　あの方程式は
>液体の圧力は水平方向ではなく表面の法線の方向に働くので
このとおり、表面の法線方向の関係に直されていますし、それが「自由境界におけるLaplace の関係」そのものですよね。
>というのは液体の圧力は水平方向ではなく表面の法線の方向に働くので、
>ヤング率が大きくなる程半球に近付くはずです。

　単に液体の自由境界を計算するときと同じように解けば、あの文章の末尾に
>ちなみに「水風船バストモデル」は無重力下ではどのような
>形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。
と書いたように仰るとおり半球に近づくように一見思えます。
　ここで無重力下というのは、皮膚の張力が重力に較べて十分大きい、ということなわけで「ヤング率が大きくなる」のと同じなわけです。

　ところがところが、です。
「あの方程式を解くときの境界条件は胸板側の長さ・バストの体積を先に決めています。」
　また、「あの座標軸の下で方程式を解く」ために、あの方程式はY,B(Y)の一対一の対応を必要としています。それが、「バストが本当に垂れてしまうような状況は考えていなかったりするので」という前提ですね。

　この二つの境界条件・前提の下で、「ヤング率が大きくなる程半球に近付くはず」が本当に正しいかどうか、考えてみては如何でしょうか？
　この二つの条件を除外しようとすると、方程式を作って解くのがとたんにメンドーになります。
というわけで、一般化されたバスト方程式をぜひ作って解いてみて下さい。

■「雪だるま」がいる景色　

大きな影の下で

　私の職場は暖かな場所にあるので、一年を通してほとんど雪が降ることはない。それでも、先日の大雪では私の職場にも雪が積もった。今年はまるで毎週末に雪が降っているような感じさえする。

　雪景色ももちろんきれいなので、ずっと眺めていたいわけではあるが、道や駐車場には除雪をしなければならない。というわけで、除雪をした時に出たたくさんの雪を使って、雪だるまがたくさん作られていた。下の写真は、雪が降った三日後に撮った。夜、明かりの下の街路樹を眺めている雪だるまの後ろ姿である。
 

夜、明かりの下の街路樹を眺めている雪だるま

　とてもずんぐりむっくりな感じで、ちょっと頭でっかちで、作者のセンスを感じさせる雪だるまのベストプロポーションである。もちろん、色々な雪だるまがいて、色々なプロポーションの雪だるまがいるわけではあるが、どれもちょっと小太りの良いお父さんという感じだ。

　もちろん、そんな雪だるま達も陽に照らされて、だんだんと小さくなっていく。下の写真は雪が降ってから四日後に、日陰で佇む雪だるまの親子だ。ずいぶんと小さくなってしまっている。
 

日陰で佇む雪だるまの親子

　この雪だるまを作った人は、消火栓の施設の日陰になるような場所に雪だるまの親子を佇ませたわけである。きっと、それは偶然ではないだろう。その人は、何かを考えた上で、雪だるまの親子の居場所としてこの場所を選んだはずだ。施設管理の邪魔になる消火栓の施設の前に、あえて雪だるまの居場所を作ったことは、とてもとても趣のあることだ。

　ところで、この雪だるまを見るとずいぶんと頭が小さくなっている。胴体の大きさに較べてずいぶんと頭が小さい。雪だるまが作られた最初の頃の体のバランスとはずいぶん違うものになってしまっている。なぜ、こんな形に変化してしまったのだろうか？

　考えてみればこんな形に溶けていくのもあたりまえなのである。雪が溶けていくスピードは雪が得る熱量に比例するだろう。それは、雪の表面積に比例するのが自然である。雪が外界から、境界としての表面を介して熱を得て、そして溶けていくのである。雪だるまのような球からなる物体では球の半径の二乗に比例し、一方、球の体積は球の半径の三乗に比例するわけだ。だから、雪で作った球が溶けていく量を体積で正規化すれば、大きい球ほど遅く溶け、小さい球ほど早く溶けていくということになる。そう、雪で作った球は大きいほど溶けにくいのだ。

　ところで、雪だるまの胴体に較べて頭は比較的小さい。だから、雪だるまの頭の方が早く溶けてもっと小さくなる。それに対して、胴体の方は大きいので比較的遅く溶けていく。結局、上の写真のように大きな胴体に小さな小さな頭がついているような形に変化していくわけである。もちろん雪だるま全体としても同じ話なわけで、大きい雪だるまほど溶けにくくて、小さな雪だるまほど早く溶けてしまうことになる。
 

　そういえば、日の当たる駐車場に佇む雪だるまの親子もいた。陽の当たるアスファルトの上で、親雪だるまは子雪だるまの南側に立っていた。そして、小さな子雪だるまは大きな親雪だるまの影の中でじっと座っていた。親雪だるまは大きかった。だから、強い日差しに照らされても、きっと溶けはしないだろう。そして、小さな雪だるまは親だるまの影の中にいれば、小さくてもまだまだ大丈夫かもしれない。少なくとも、次に雪が降るまでは大丈夫かもしれない。次に雪が降れば、また雪だるまは大きく増えていくことだろう。

　今年は毎週末に雪が降っているような感じさえするくらいだから、きっと大丈夫なんだと思う。
 

■あなたの声が、すぐそばにある　

高原の向日葵と月見草 編

　昨日、東京駅の地下街にある「王様のアイデア」でこんなものを買った。見ての通り、ピストル型の集音マイク"SonicExplorer"だ。その数日前にその集音マイクを初めて見かけたのだが、遊んでみるとどうにも気に入ってしまって、次に見た時には必ず買おうと決めていたのである。
 

Sonic Explorer

　数日前に、その"Sonic Explorer"を見かけた時は出張帰りだったのだが、地下街の雑踏の中で「頭にヘッドホンを被り、ゴルゴ13のように集音ガンで狙っている」様子はさぞかしアブナイ奴に見えたに違いない。現に、私が雑踏の中に"SonicExplorer"で狙いをつけていたときには、一緒に出張していた仲間が二・三歩後ずさりして、私の側から離れていったくらいである。自分でも怪しい姿だとは思ったのだが、そんなことを忘れてしまうくらいに面白かったのである。こんなおもちゃみたいな外見に似合わないほど、これを使うと遠くの音がピンポイントでよく聞こえるのだ。地下街の雑踏の中で遥か向こうで携帯電話で話をしている人に"SonicExplorer"を向けると、私の耳元でささやいているかのように聞こえてくるのである。もちろん、遥か向こうといってもたかだか20mくらいではあるのだが、雑踏の先の20mというのはずいぶんと先に感じる。しかし、"SonicExplorer"の先のパラボラ面は見事にその遠く先の音を集めてくれる。

　ところで、遠く離れた人の声はどうして聞き取れないのだろうか？それはもちろん、遠く離れた人の声は小さくしか聞こえなくなって、その人以外が発する雑音に埋もれてしまうからだろう。それでは、人がしゃべる声は距離が離れるとどの程度小さくなるだろうか？
　音波が四方八方に等方に拡がっていくとすれば、音の大きさは音の発信源からの距離の二乗に反比例すると考えるのが自然である。つまり、喋っている人からの距離が10倍になれば、その人の声は1/100の大きさでしか聞こえないことになる。20m先で携帯電話で喋る人の声は、1m隣でささやく人の声のわずか1/400の大きさなのである。それでは、雑踏の中で溢れる他の音に埋もれてしまうのは当り前である。

　そんな声を聞き取りたい時にはどうしたら良いだろう？そんな時、私達は耳に手を当てて、耳を澄ませる。掌で音を耳に集めて何とか声を聞き取ろうとするのである。それと同じく、この"SonicExplorer"は、先端のパラボラ面で焦点にあるマイクに音を集めて増幅するのである。それでは、"SonicExplorer"は私達の耳に比べてどの程度音を多く集めているだろうか？

　そもそも、私の耳の大きさはどの程度だろう？耳はそんなに効率的に音を集めそうな形状をしているわけではなさそうだから、有効な集音面積としては直径1cmの円といったところだろう。それに対してこの"SonicExplorer"のパラボラは直径20cm程だ。ということは、直径にして20倍、面積にして二乗で400倍の面積で音を集めることができるわけである。音を集める程度は音を集める面積に比例するだろうから、"SonicExplorer"を使えば人間の耳の400倍もの鋭さで音を聞き取ることができるわけだ。400倍ということは、つまりは先ほどの「20m先で携帯電話で喋る人の声」と「1m隣でささやく人の声」との違いと同じというわけで、結局のところ"SonicExplorer"を使えば「20m先で携帯電話で喋る人の声」が「1m隣でささやく人の声」であるかのように聞き取ることができる、ということになる。

　ここで面白いのは、音が小さくなってく様子は距離の二乗に比例し、音を集める量は集音面のパラボラの直径の同じく二乗に比例するから、n倍遠くの音を元と同じように聞き取りたかったら、集音面の大きさ（長さ）をn倍にしてやれば良い、という単純な関係にあることである。20m先の声を1m横の声と同じように聞き取りたかったら、耳の大きさ（長さ）を20倍にしてやれば良いのである。

　そんなことを考えていると、ふと二十年位前のことを思い出した。その頃、私は夏になるといつも長野県の野辺山あるいは川上村というところに滞在していた。その数年前まで、私はその野辺山で暮らしていたのである。そして、野辺山にある45ｍミリ波望遠鏡の建設が佳境に入った頃だったのだろうか、その頃私の父は半分野辺山で暮らしていた。下の写真は八ヶ岳の麓にあるその45ｍミリ波望遠鏡である。
 

野辺山45ｍミリ波望遠鏡

http://www.icon.pref.nagano.jp/usr/minamimaki/sawayaka.htm

　そんな二十年位前のある日、父がこんなことを言った。

「45ｍのアンテナを赤岳（八ヶ岳の最高峰）に向けて、副鏡（焦点）の場所にいると赤岳の上にいる登山客達の話す声がまるで自分のすぐ横にいるかのようにガヤガヤと聞こえてくるんだよ」

　そこで、試しに地図で野辺山の45m望遠鏡と赤岳の山頂の距離を確かめてみると、直線距離にして10km程である。下の地図で赤い■の位置辺りが野辺山の45m望遠鏡が建っているところだ。10kmということは、メートルにして一万メートルである。メートルに直したところで、やっぱり遠いことには変わりない。
 

野辺山の45m望遠鏡（赤■）と赤岳の山頂の距離

それでは、先ほどの"Sonic Explorer"と同じように考えてみることにしよう。45m望遠鏡のパラボラ面は人間の耳（ここでも直径1cmとしよう）の45m/1cm= 4500cm / 1cm = 4500倍である。ということは、5000m先、すなわち5km先の音が1mのすぐそばにいる人の声と同じように聞こえるということになる。すると何ということだろう、10km先の八ヶ岳の山頂でワイワイガヤガヤと話す登山客達の声は、すぐ2m横でワイワイガヤガヤと話しているかのように聞こえることになる。もちろん、それは理想的な場合の話ではあるが、先の父の話は結局のところ何の不思議もないごく当り前の話だったわけである。
 

　上の写真のような、八ヶ岳の麓にそびえる白い45m望遠鏡ももちろんかっこいいけれど、私が野辺山に住んでいた頃にはまだその45m望遠鏡は建っていなかった。私がいた頃には、下の写真の中に見える朱色の野辺山太陽電波観測所の野辺山干渉計のパラボラアンテナだけが野辺山の高原に点在していた。野辺山干渉計はもう今では現役ではないけれど、今でもやっぱりイースター島のモアイのように大空に向いているはずだ。私は白く輝く45m望遠鏡も大好きだけど、その横に点在している朱色に塗られた鉄骨で支えられている野辺山太陽電波観測所の野辺山干渉計の方が大好きだ。
 

野辺山太陽電波観測所の野辺山干渉計（朱色のパラボラアンテナ）

http://solar.nro.nao.ac.jp/nori/html/introduction-j.html

　現役を引退した今ではどうなのだか知らないけれど、野辺山太陽電波観測所の野辺山干渉計のパラボラアンテナは太陽電波を捕らえるためのアンテナだったので、いつも太陽の方を向いていた。まるで、巨大な向日葵のように忠実に正確に太陽のある方向にパラボラ面を向けていたのである。だから、太陽が強く照らす晴れた日も、薄暗い雨の日も朱色の鉄塔の上のパラボラアンテナを見れば、太陽の方角はいつも一目瞭然だったのである。

　そういえば、私が子供の頃、一時間かけて歩く家から分校までの4キロメートルばかりの道端には、たくさんの月見草が咲いていた。高原の中で高くそびえる赤く巨大な「向日葵」達と、歩く私のすぐ横に咲いている黄色い「月見草」が私はとても大好きだった。

　眩しい太陽を追いかける「向日葵」達も、静かに照らす月を見る「月見草」もどこか遠くの声を耳を澄ませて聞いているのだろうかとか、その声をすぐそば近くに感じているのだろうかとか、少し思ってみたりした。

■水平線の彼方　

Over The Horizon

　先日、富士の五合目から地平線を眺めていたのだけれど、そこで「水平線の向こうには何があるのだろう？」なんてことをふと頭に浮かべてしまった。「そこまでしか見通せない」という線が水平線なのだから、もちろん水平線の向こうに何があるのか見えるわけがない。だけど、だからこそ「その水平線の向こう」に何があるのかが、少しばかり気になってしまった。
 

　そういえば、少し前に英和辞書を読んでいた時に、" on [over] the horizon"で「兆しが見えて,将来起こりそうで」を意味する、なんて書いてあった。「水平線の向こう、水平線の彼方」にある「何か」は「将来起こりそうな、何かの兆し」というわけだ。
　あぁ、そうかぁ、と私は思わず納得してしまった。確かに、水平線の向こうに例えばもし何かの波があれば、それはきっといつか私たちの目に見えるようになって、そして私たちの足元にまで辿り付くことだろう。水平線の向こうにある波は止まることなく進み続けているのだから、例え水平線の向こうにあっても将来必ず私たちの場所まで辿り着くのである。

　もちろん、水平線の向こうにある波を私たちが見通すことはできるわけはないのだけれど、だけどその気配を私たちはきっと感じるのだろうと私は思う。「水平線の彼方」にあるものは、「将来起こりそうな何かの兆し」であって、水平線の向こうにいるその気配には強い存在感があるはずだろう。
 

　そんな「水平線の彼方にある波」を考えるとき、私はこんな話を思い出す。
 

　地球はよく「水の惑星」と呼ばれる。確かに、そう呼ばれるくらいに地球には水が溢れている。何しろ、地球の表面積の七割が海なのだ。しかし、そうは言っても、地球の表面が全部水に覆われている、というわけではない。私たちが生活している陸地だって、「残りの三割だけ」とはいえちゃんと存在している。

　それなら、表面全部が水で覆われている「水の惑星」がもしもあったとしよう。そんな水の惑星のどこかで高い津波が生じたら、一体どうなるだろう？例えば、その水の惑星の南極である日突然津波が生じたとしよう。その時その津波はどんな風に伝わっていくだろう？

　その津波の動いていく様子を図示してみたのが、下のアニメーションだ。

 
　南極（図の下部）で発生した津波は進むに従って、段々と小さくなっていく。最初は南極の一点に集中していたエネルギーが段々と広がって拡散していくのだから、波が進んでいくにつれその高さはどんどん低くなる。そして、赤道を通過する頃には津波の高さはとても小さくなってしまう。

　ところが、その波が赤道を過ぎたとたんに津波は逆に強まりはじめる。赤道を通過した後は、津波の前方はだんだんと狭まっているので、こんどは津波のエネルギーが集まり始めるわけだ。それまでは、低くなる一方だった津波の高さは、今度は逆に徐々に高くなっていく。そして、ついに津波が北極に辿り着く時には、かつて南極で津波が発生したときの高さを再現してしまう。生まれた地点のちょうど反対側で、津波が生まれたときと全く同じ高波が発生するのである。

　私たちの裏側で津波が発生したとしても、その津波は徐々に小さくなりながら進み続け、そして私たちの足元でその津波は再び大きな高波となるのである。そして、その津波はその後も同じように進み続けて、また南極で大きな高波となる。南極から発した高波がもう一度南極に集まってまた高波となるとも言うことができるかもしれないし、あるいはそれは、北極で集まった高波が南極で集まってもう一度同じ高波となる、とも言えるだろう。

　そしてまた、「水平線の彼方にある波」はそれと似たこんな話も思い出させる。
 

　宇宙の曲率が正で閉じた球状空間だった場合、私たちが発した光はどうなるだろう？　私たちからどんどん離れて行く光は空間の四方に広がって行くが、何時の間にかその光は徐々に近づき始める。そして、はるか彼方のある一点でその光が集まり、そしてまたその光は広がり始める…。そしてついには、その光は私たちのいる場所に集まり始める。私たちを取り囲む全ての方向から、かつて自分が発した光がやってくることになる。

　かつての自分があらゆる方向に見え出すのである。

　水平線の彼方には何があるのだろう？水平線の向こうを見通すことは、私たちにはできないけれど、遥か彼方にいる波は「将来必ず私たちの足元に訪れる」。そして、もしかしたらそれは「かつての自分が発した波」かもしれないし、「どこか自分と正反対の場所にいる誰かが発した波」かもしれないし、それは廻り回ってやっぱり、「自分が発した波」なのかもしないし、やっぱりそれとも…なんて考えてしまったのである。
 

■純愛で世界を描ききれ　

Study of the Regular Division of the Plane with Innocent Love

　先日、出張先で話をしようとした途端、いきなりこんなコトを言われた。

「最近、更新頻度が下がってますねぇ、あとアッチ系のネタが多いですねぇ。」

「たかが風圧がオッパイに思えるものでしょうか？自分には、そこがなんとも不思議で納得できないのであります。」
「一体、指の何処でその感触を感じると思われますか？」
「それに、モンローウォークの動画はまるで全裸みたいに見えて、思わず自分はウィンドーを閉じてしまったのであります。」

「いや、掌の広げ方次第で、空気が指に与える圧力が動的に変化するのだが、その指の動きに応じて動的に弾力が変化するさまがアノ感触に近いという想像は如何なものだろうか？たかが風圧、されど風圧、と謙虚に考えるべきではないだろうか？」

「空気流が指の側面を押す力が主たる個所だろう、それすなわち、指の周りからこぼれるおちるアレが指に与える感覚なのである。」

「実はOLスーツ編の動画も作成したのだが、そっちの方が私的にはイヤラシク倫理的にNGだったのだ。」

　そこで、そんなことを言われないために、今回は「できるかな?」のスタート地点である「画像」の話題を考えてみたい。しかも、ただ考えるだけではつまらないので、「できるかな?」風に「愛」を込めて「画像」について考えてみたい、と思う。というわけで、今回は題して「純愛で世界を描ききれ」である。
 

　八月に台風が関東地方を直撃した日、私は東京タワーのすぐ横で「高画質化のための画像処理技術」という研究会を聴講していた。会場に辿り付くまでの間ひどい雨と風に襲われて、最初のうちは「こ・これは、風速25m/s位はあるな。ってことは25mx 3600 s /1000mで時速90kmか…ってことは、計算によればE〜Fカップが今まさに体中にぶつかってきているのかぁ！」なんて（自分を元気づけるために）考えていたのだけれど、風だけでなくて雨もひどかったので、ついには濡れねずみになってしまい、ただ「………」と何も考えずとぼとぼ歩くだけのゾンビ状態になってしまった。

　何はともあれ、そんな感じでやっとのこと会場に辿り付いて、いくつかの話を聞いていたのだけれど、その中でもとても面白かったのが、大日本印刷の阿部淑人氏の「シミュレーテッド・アニーリングによるディザマトリックスの最適化」という話だった。色々な項目を適当に重み付けしながら、ハーフトーンパターンを自動で生成して、理想のハーフトーンパターンを作成しよう、というものである。その話の後半では、工芸的なスクリーンの話も俎上に上がり、M.C.Escherの"Sky& Water I"をグラデーションの例に挙げてみたり（残念ながら実際にそんなハーフトーニングをしたわけではないが）、菩薩像を般若心経でハーフトン処理してみせたり、となかなか「できるかな?」心をくすぐるものだった。そこで、私も似たようなことにチャレンジしてみて、さらにはM.C.Escherの版画を使ったハーフトーニングを行ってみたいと思うのである。
 

M.C.Escher　Sky & Water I　1938

　そもそも、ハーフトーニングとは多値階調を持つ画像などをニ値出力の（もしくは少ない階調しか持たない）機器で出力するために、多値の階調をニ値（もしくは少ない階調）の面積比率で置き換えることにより出力する方法のことである。例えば、下の例はグレイスケールのグラデーションパターンを円スクリーンによりハーフトーニングしたものである。
 

グラデーションパターンを円スクリーンによりハーフトーニングしたもの

グレイスケールのグラデーションパターン 上を円スクリーンによりハーフトーニングしたもの

 Photoshopを使っている場合には、簡単に任意形状のハーフトーニングを行うことができる。例えば、こんなパターンをカスタムパターンとして登録すると、そのパターンとの明暗比較を行うことにより、
 

という風にニ値化ハーフトーニングを行うことができる。ところが、じゃぁこれと同じようにEscherの版画を使ってハーフトーニングしようと思っても、そう簡単にできるわけではない。なぜなら、このハーフトーニングが明暗比較によって行う以上、ハーフトーニングに使うパターンは多値の画像でなければならないのである。

　Escherの版画も版画という（例えば白か黒かといった）ニ値の出力機器を用いているため、やはりニ値の画像に過ぎない。例えば、下の版画はEscherの”Studyof the Regular Division of the Plane with Horsemen”である。
 

Study of the Regular Division of the Plane with Horsemen　1946

　上の版画の一部を（ちょっとだけ細工をしつつ）抜き出してみたのが下の画像だが、白黒半分づつのニ値画像であることがわかるだろう。また、きれいな繰り返しパターンになっていて、平面にこのパターンできれいに埋め尽くすことができるのがわかるだろう。
 

上の画像の一区画（黒：白の比率は厳密に1:1）

　この画像をPhotoshopのカスタムパターンを用いて、グレイスケールをニ値化ハーフトーニングすると、この画像がニ値画像であるため、下のように階調をきれいに出力することができず、結局のところ「黒か白か」といった階調飛びの画像になってしまうのである。
 

ニ値画像を使って単純にハーフトーニングしようとすると…

グレイスケール

単純にパターンニ値化すると…

　そこで、まずはニ値の画像を元に多値のハーフトーン用パターンを作成するプログラムを作成してみた。作成するやり方としては、初期値を元にして暗い方。明るい方それぞれの方向にローパスフィルターで演算をしつつ、256階調分のハーフトーンを作成し、さらにそれをPhotoshopで処理できるように多値画像として出力することができるようにしてみた。先の発表のやり方で言えば、「高周波を減らす」という項目に重みをおいて、ハーフトーンパターンを自動生成するアプリケーションを作成してみたわけだ（バグ満載状態で）。説明は一切無し、しかもボタンを押す順番を間違えると上手く動かないという状態ではあるが、一応ここにおいておく。名前はhiraxtone.exeでバージョンは0.0…01という感じである。（白黒ニ値だけど24bitモードの）Bitmapファイルを読み込んで、多値のスクリーンを生成するようにしてある。

• hiraxtone.lzh 403kB

右：オリジナルのニ値画像
左：ニ値画像を元に作成した多値階調ハーフトーンパターン

　でもって、上で作成した多値階調ハーフトーンパターンを用いて、グラデーションパターンをハーフトーニングしてみた例が下の画像である。「単純にパターンニ値化した場合」と違って、「hiraxtone1で作成したパターンを使用した場合」はグラデーションが保持されているのがわかると思う。また、階調が保持されているというだけではなくて、まるでEscherのオリジナルの"Studyof the Regular Division of the Plane with Horsemen"のようなパターンにできあがっていることも判ると思う。
 

hiraxtoneで作成したパターンを使用してグラデーションパターンをハーフトーニングすると…

グレイスケール

単純にパターンニ値化した場合

hiraxtone1で作成したパターンを使用した場合

　さて、ニ値画像パターンを利用してハーフトーニングすることができる、となると他にも色々と遊ぶことができる。例えば、自分だけのハーフトーンパターンを作ってみたくなることだろう。そして、さらにはその素晴らしいスクリーンに自分の名前を付けて広めてやりたい、と思うのは至極当然の話である。古くはBayerなどがそうしたように、自分が作ったスクリーンに自分の名前をつけてみるわけだ。

　とはいえ、私が仮にスクリーンを作成してみたところで、そのスクリーンを私の名前で呼んでくれる保証はどこにもないのである。そこで、卑怯な手ではあるが、自分の名前を元画像にしてスクリーンを作成してみることにした。こうすれば、否でも応でもこのスクリーン形状を呼ぶために人は私の名前を使うことになるわけだ。

　というわけで、私の名前「純」という漢字を元データにして、ハーフトーンスクリーン「純」を作成してみた。また、「純」とくれば当然もうひとつ「愛スクリーン」もさらに作ってみた。いや、別に「純愛」を目指そう、と気負っているわけではなくて、単にうちの兄弟は長男が「純」で長女が「愛」なのである。いや、少し気恥ずかしいけど、ホントの話そうなのだからしょうがない。

　さて、作成した「純・愛スクリーン」さえあれば、「純愛」で世界を描ききることができるわけで、早速描いてみたのが、下の仲間由紀恵である。オマエの世界イコール仲間由紀恵か？とか、ソレってホントに「純愛」か？とか、つまらないツッコミを入れられそうな気もするが、そんなことはどうでも良いのだ。私はTRICK以来仲間由紀恵のファンになってしまったのだから、しょうがないのである。そしてまた、「純愛」を馬鹿にしてはイケナイ、と私は少しばかり思うわけなのである。（私の名前だから）
 

「純愛スクリーン」でハーフトーニングした仲間由紀恵

「純」スクリーンで描く仲間由紀恵

「愛」スクリーンで描く仲間由紀恵

　上の二枚をじっくり眺めてみると、結構キレイに仲間由紀恵が描かれていることが判ると思う。しかも、他でもないこの二枚の画像において、私は「純愛」で仲間由紀恵を描ききっているのである。これより、「純」で「愛」な仲間由紀恵はそうそういないハズなのだ。きっと、本物の仲間由紀恵が見たら「何てピュア〜でラブリーな私かしら。きっと、これを描いた人は心のキレイな人なのね！」と感激すること間違いなし、なのだ。

　ちなみに、「純愛スクリーン」でハーフトーニングした仲間由紀恵の左眼の部分を拡大してみたのが下の二枚の画像である。瞳の奥にも、「純」と「愛」が溢れていることが判るハズである。それは言い換えれば、この仲間由紀恵の瞳は「純」イコール「私」で満ち溢れ、さらにはその瞳は「愛」で満ち溢れているのである。
 

仲間由紀恵の目の部分の拡大図

「純」スクリーンの仲間由紀恵 （目の部分の拡大図）

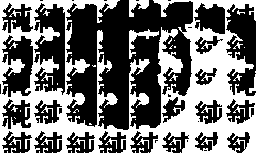「愛」スクリーンの仲間由紀恵 （目の部分の拡大図）

　う〜ん、正直ちょっとムナシイけれど、だけどちょっと気持ちが良いのもまた事実なのである。やはり、「純・愛スクリーン」で描かれる世界はとても素晴らしい世界なのである。そうなのである。

　さて、今回作成したhiraxtoneは、実際のところ自分でも言うのもなんだが、本当のところ今ひとつキレイな出力ができないし、大体思ったように動いてくれないのである。低周波優先として重み付けをしたハズなのに、どうもそんな風に動いていないし、計算にも時間がかかりすぎる。全てはビールを飲みながら行き当たりばったりにプログラミングするところがいけないのかもしれないが、どうも今ひとつなのである。また、本来であればもう少し元データの形状を残すことを優先（それは高周波優先にならざるをえないだろう）にするようなオプションもつけてみたいのである。

　が、とはいえ今回はいい加減思いページになってきたこともあるし、ちょっと疲れてきたこともあるし、とりあえず「純愛」で世界を描ききったところまでで今回は終りにして、続きは次回以降に遊んでみたいのである。