hirax.net::Keywords::「予測」のブログ

トップページ"hirax.net" へ　/　サイトBlog "inside out" へ

「予測」に関する最新記事　/　「予測」に関する「説明」「記事の一覧」
より新しい5件の記事へ

1999-12-21[n年前へ]

■恋の力学　

恋の無限摂動

クリスマスが近くなると、街のイルミネーションが綺麗に輝き始める。いかにも、ラブストーリーが似合う季節である。そこで、今回は、"Powerof love"、すなわち、「恋の力」について考えてみたいと思う。「恋の力」により、人がどのような力を受け、人がどう束縛されるのか、などについて考えみたいのである。また、恋に落ちたカップルがどのような行動をするのかについて解析を行ってみたい。

「できるかな?」では以前、

鴨川カップルの謎 -そうだ、京都、行こう-(1998.11.29)

において、カップルが他のカップルを意識する力について考えたことがある。カップル同士の間に働く斥力を考えることにより、鴨川カップルの行動を考えてみた。それと同様に、今回はひとつのカップルのみを考え、その中に働く力を考えてみるのである。ひとつのカップルの「男」と「女」の間にどのような力が働くかを考えるのである。

そういうわけで、今回の登場人物は「男」と「女」である。その二人は「恋に落ちた二人」である。二人の間には「恋の力」が働いているのだ。その二人の間に働く「恋の力」について考察することにより、恋に落ちたカップルの行動について考察を行ってみることにする。

といっても、「恋の力」を精密に測定した報告例は未だ存在しないので、ここでは適当な値を用いていくことにする。「恋は距離に負けない」とか「遠くて近きは男女の仲」などとははよく言われる。そこで、距離によらないと近似した。また、「遠くて近きは男女の仲」の意味を考えれば、恋の力は無限遠まで働く力である、と考えるのが自然である。
そこで、今回の「恋の力」は距離に関わらず一定であると仮定した。距離=rとした時に-r/Abs[r]の大きさで「相手に惹かれる」ものとした。仮に第一種「恋の力」(仮称)とでもしておく。

今回は「恋の力」は距離によらないものとした。しかし実際は、(通所の距離においては)「男」と「女」は距離が近いほど惹かれ合うし、離れてしまうと惹かれ合う力は弱くなるというのが自然であると思われる。そこで今回の第一種「恋の力」(仮称)は、あくまで大雑把な近似ということにしておく。

恋する二人の間に働く力をもう少し正確に記述しておくと、

「恋の力」 = - 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」

であり、恋する二人には「(hiraxの)恋の運動方程式」

「恋の力」=優柔不断度 *　「恋の加速度」

が成立する。ニュートンの運動方程式に少し似ているが、かなり異なるものである。ニュートンの運動方程式との違いは、「質量」にかわるものが「(hiraxの)恋の運動方程式」においては、「優柔不断度」
であることだ。心がトキメいてもなかなか行動を起こすことが出来ない人がいるだろう。そういう人は「優柔不断度」が高いというわけである。恋の行動における慣性を示すパラメータである。

また、今回は空間を1次元であると簡略化してみた。1次元の空間の中で「男」と「女」が動き回るのである。その時間的変化を調べてみるのだ。従って、シミュレーション結果は空間軸が一次元+時間軸一次元で、合わせて2次元となる。

さて、この「恋の運動方程式」を解くことにより、恋する二人の行動は予測することが可能となるわけだ。試しに、その計算サンプルを示してみる。なお、今回は時間方向で数値的に逐次解を求めている。

初期状態は

「男」位置=5, 速度=0,魅力=100,優柔不断度=10
「女」位置=0, 速度=0,魅力=100,優柔不断度=10

とした。すなわち、「男」も「女」も二人とも停止した状態で恋に落ちたのである。「二人は立ち止まって恋に落ちた」というやつである。一番良くあるパターンであろう。もちろん、「すれ違いざまの恋」といったような初期速度を持つ恋愛パターンも存在するが、今回はパスしておく。
位置や時間の単位は任意単位である。「0」と「5」は東京と大阪であっても良いし、ロンドンとニューヨークであっても良い。あるいは、実空間でなく精神的な空間と考えてもらっても構わない。すなわち、心の動きを示しているものとするのである。
また、二人の「魅力」や「優柔不断度」は対等である場合だ。その結果を下に示す。このグラフは縦軸が空間位置であり、横軸が時間である。黒線が「男」であり、赤線が「女」である。
　

恋する二人の軌跡(「男=黒」と「女=赤」が対等な場合)

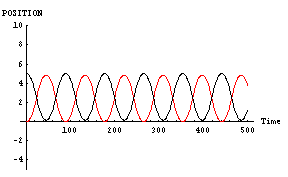「男」と「女」が同じように相手の方向へ向かっているのがわかると思う。これが「恋の無限摂動」である。こういった「恋の無限摂動」の代表的なものには「君の名は」の主人公達の動きなどがある。恋に落ちた二人が、延々とすれ違いを続ける物語である。これは、この「男」と「女」の行動そのものである。

この計算結果では「男」と「女」が糸を紡いでいるようにうまく絡みあっているのがわかる。「恋の無限摂動」の幸せなパターン例である。これは、「男」と「女」が対等であったことがその一因である。

その証拠に、「男」と「女」が対等でない場合の計算結果を示してみる。次に示すのは、

「男」位置=5, 速度=0,魅力=10,優柔不断度=10
「女」位置=0, 速度=0,魅力=100,優柔不断度=10

の場合である。すなわち、「男」の魅力が「女」の十分の一である場合だ。
　

恋する二人の軌跡(「男=黒」の魅力が「女=赤」の1/10の場合)

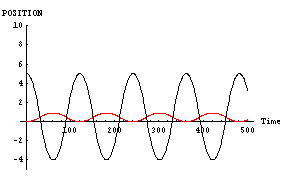「男」が右往左往するのに対して、「女」はほとんど動いていないのがわかると思う。おそらく、この場合には「男」と「女」の「心」もこれと同様のパターンを示しているものと思われる。すなわち、「男」の「心」は揺れ動いているのに対し、「女」の「心」はほとんど動いていないのである。

先の例と異なり、これは実に不幸な計算例である。不幸ではあるが実際によくある例であると思う。以降、これを「男はつらいよ」パターンと呼ぶことにする。「女」に「男」が振り回されているパターンだ。もし、奇跡的に結婚などしても、将来どうなるかは火を見るより明らかである。

それでは、「男」と「女」の「魅力」が同等で、かつ、とてもスゴイ場合を示してみる。すなわち、ドラマの主人公達のようにとてつもなく魅力的な二人が恋に落ちた場合である。一般人とは違う二人が恋に落ちたら、果たしてどのような行動を示すのであろうか?この場合のパラメータは以下に示す、

「男」位置=5, 速度=0,魅力=1000,優柔不断度=10
「女」位置=0, 速度=0,魅力=1000,優柔不断度=10

である。
　

恋する二人の軌跡(「男=黒」、「女=赤」の魅力が両方1000の場合)

この場合、見てわかるように「男」と「女」は激しい動きをしながら、絡み合う。芸能人で言うならば、小柳ルミ子夫妻の場合などが挙げられる。まるで、激しいダンスのように「男」と「女」は絡み合うのである。
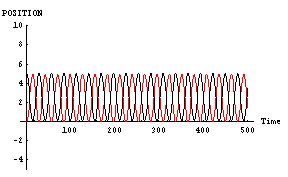「魅力ある二人が恋に落ちた場合には、あまり近づかない方が良い」という教訓をここから得ることができる。

最後に、「男」と「女」の二人ともにあまり魅力がない場合である。パラメータとしては、

「男」位置=5, 速度=0,魅力=2,優柔不断度=10
「女」位置=0, 速度=0,魅力=2,優柔不断度=10

の場合である。
　

恋する二人の軌跡(「男=黒」、「女=赤」の魅力が両方2の場合)

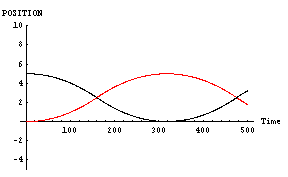これなど「恋」と言えるのかどうかもわからない位である。ほとんど、「ただすれ違っただけの相手」である。これがさらに進むと、魅力がお互いに0同士のパターン、

「男」位置=5, 速度=0,魅力=0,優柔不断度=10
「女」位置=0, 速度=0,魅力=0,優柔不断度=10

の場合となる。下に示すように、
　

恋する二人の軌跡(「男=黒」、「女=赤」の魅力が両方0の場合)

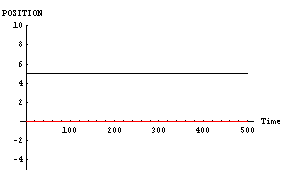これっぽっちも「男」と「女」は「恋」に落ちていないのである。これではカップルの「男」と「女」ではなく、単なる他人である。

さて、今回は行わなかったが、カップルに「恋のエネルギー損失」を導入することにより、「恋の無限摂動」を減衰させることができる。それにより、現実のカップルの行動にさらに近づくことができるのではないかと、私は考える。何らかの抵抗が生じることにより、「恋の無限摂動」が減衰するのだ。そして、二人は接近した状態で停止するわけだ。

さて、今回の登場人物は「男」と「女」だけであった。しかし、現実でも、ドラマの中でも、通常は多くの登場人物が登場する。登場人物が「男」と「女」だけというような理想的な条件のみではない。
人の恋路を邪魔する(主人公からすれば)ヤツも必ず登場する。また、特定の登場人物の間では斥力が働くだろう。そのような場合、一体どのような現象が生じるのだろうか。

そもそも、今回の恋する二人の行動パターンは予測可能であったが、現実そのようなことがあるだろうか？果たして、未来の行動パターンは予測可能なのだろうか？色々な登場人物が現れる場合にも、今回の結論は成立するのだろうか？

それらは次回の課題にしておく。題して、「恋の力学三角関係編- 恋の三体問題- (仮称)」である。「恋の力」を一般化し、多体問題として解いてみたいのである。恋する人達とその周りの人達がどのような行動をするか、恋の三角関係においてどのような力が働いているのか、について解析を行ってみたい。今回は、そのための前準備というわけである。
　

この記事の「関連お勧め記事」を読む >>

2000-02-02[n年前へ]

■日出ずる処のダイナブック　

東芝ノートの発表日の秘密

東芝の作るノートPCはアラン・ケイが考えた"Dynabook"という名前で呼ばれる(日本では)。その名に恥じないように、東芝もノートPCに関しては力を入れまくりのハズである。

私も歴史は浅いが数台にわたって東芝ノートのユーザーである。ポインティングデバイスなどは、東芝のトラックポイントとボタンでないと耐えられない体になってしまった。いや、本当に。
　しかし、使い始めて年月が経つと性能の低下や不具合が出てくる。特に、ケースが割れまくる機種などを使っていると、なおさらである。

そうなると、どうにも新製品が気にかかってくる。「早くいい新製品が出ないかな」と熱望するようになるのである。

そういう気持ちは誰しも抱くと思われ、NiftyのフォーラムやWEB上の掲示板を眺めてみても、新製品の噂情報は数多く溢れている。

中でも、

どんな新製品が ( What )
いつ出るのか ( When )

というのは非常に重要である。何しろ、自分がPCを買ったとたんに新製品が発表されたりすると、大ショックを受けてしまう。自分の付き合い始めた彼女が、実は友人とずっと付き合っていた、と聞くようなショックである。いや、少し違うな。

だからといって、掲示板で「私はいつPCを買えば良いのでしょう？」などと尋ねたりすると、

「欲しいときに買えェ。」 (By スタパ斎藤)
「そんなことは自分で決めろ。」

などと言われること必至である。

だから、新製品を買うべきか買わざるべきか、というジレンマに私たちは頭を悩まされることになる。まるで、ハムレットである。

そもそも、このジレンマの理由は新製品の発表が前もって知ることができないという点にある。いつ・どんな新製品が出るかどうか判っていれば、あとは自分の判断で決めれば良いのである。
このジレンマは東芝の青梅工場に忍び込んだりすれば即座に解決できる。しかし、その場合、今度は「囚人のジレンマ」を考えなければならなくなってしまう。このような問題点のために、「東芝青梅工場に忍び込む」方法は採用すべきではない。

そこで、よく考えてみる。先の

どんな新製品が ( What )
いつ出るのか ( When )

というのをもう一度眺め、マクロな視点から考えてみよう。もしかしたら、これらは実は推定できるのではないだろうか？例えば、「どんな新製品が ( What )いつ出るのか ( When )」というのは

6502と並列計算とムーアの法則 - 人間のクロック&スケールアップ- (1999.12.30)

の時の「ムーアの法則」で判るわけだ(もちろん大雑把に)。そして、「いつ出るのか( When )」というのは統計をとってみれば、予測できるのではないのだろうか？つまり、これまでの製品の発表日を調べてみると、実は統計的規則が隠れているかもしれない。

今回は、東芝のノートPC製品の発売日を統計的に調べ、そこに隠れている規則性を明らかにしてみたい。というわけで、今回は新製品が欲しい人たちに贈る研究報告である。

　まずは、

Notebook Center ( http://www.kamikura.com/notebook/)

から最近の東芝ノートPCの発売日をピックアップしてみる。それが以下である。

機種　発売日
Libretto50 1997/1/7
Satellite220 1997/5/8
Libretto60 1997/6/24
Libretto70 1997/10/29
Satellite 300/305/310 1998/2/2
Libretto100 1998/3/5
TECRA780 1998/4/2
Satellite 1998/5/11
Satellite325/320 1998/7/27
Satellite4000 1998/8/3
Portege3010/3000 1998/8/12
TECRA8000_Satelllite4000X/4010X_PORTEGE7000LibrettoSS1010 1998/10/22
Satellite2510 1998/11/5
PORTEGE3020 1999/1/7
Satellite2520 1999/1/13
SS3300_Satellite4000 1999/1/26
SS7020X 1999/4/13
DynaBook4050X/2540S 1999/5/12
SS3330 1999/6/3
Satellite4100X 1999/6/15
Librettoff1100_DynaBookSS3380 1999/6/28
DynaBook2060 1999/8/5
Satellite2590X/2100 1999/10/14
SS3330V 1999/10/26
SS3380V 1999/12/7
Satellite4320/4260/2140 2000/1/19
Dynabook 2000/1/26

　それでは、これをグラフにしてみる。「東芝ノートPCの発売月日と曜日の散布図」である。横軸を東芝ノートPCの発売月日として、縦軸を東芝ノートPCの発売曜日とした散布図である。

東芝ノートPCの発売月日と曜日の散布図

　ここで、このグラフの曜日軸は、

0　日曜日
1　月曜日
2　火曜日
3　水曜日
4　木曜日
5　金曜日
6　土曜日

となっている。このグラフを眺めてみると、東芝製のノートPCは

火曜日〜金曜日

に多く発表されることがわかる。土日はもちろん、月曜日は一回もない。また、金曜日に発表の場合は、月のはじめが多い。
　何故、月曜日に発表しないのか、このナゾをと某メーリングリストで質問した所、幸いにもその答えを教えて頂いた。それは日付変更線と関係していたのである。

もし、日本で月曜日に新製品を発表すると、日付変更線の向こう側のアメリカではまだ日曜日である。すると、全世界で同時発表ということができない。東芝は全世界を視野におくので、全世界同時発表ができる火曜以降が良い、というわけである。その結果として「火曜日〜金曜日」になるというわけである。
　日出ずる処のダイナブックが故なのである。

また、今回の結果では発表月は1,10月が多かった。

そこで、今回の結論は