1999-11-23[n年前へ]
■ミニスカートの幾何学 
32cmの攻防戦
早朝、東名高速で事故渋滞にはまってしまった。仕方がないので、TVを眺めていると、面白い話をやっていた。それは、ミニスカートの丈の話である。何でも、最近の流行はミニスカートの丈が32cmのものであるらしい。女子高生?などが言うには、
「34cmだと長いしぃ。」だから、32cmだと言うのだ。別に、オリンピック選手でもないのだから、ミニスカートの丈の限界まで挑戦しなくても良いだろう、と私などは思ってしまう。しかし、彼女たちはそう考えないらしい。人それぞれである。
「30cmだと下着が見えちゃうしぃ。」
それにしても、スカートの丈が32cmと30cmの間でそんなに、違いがあるものだろうか? 「見える・見えない」を決める分水嶺がその2cmの違いにあるものなのだろうか? 妙に不思議である。 そこで、ミニスカートの幾何学について考えてみることにした。題して「32cmの攻防戦」である。
何より先に確認しておくが、私は今回は科学的好奇心で動いているのである。そこに、一点の不純な気持ちも存在しないことを、ここで確認しておく。いや、むしろ、女性のためのミニスカート理論の構築を目指しているといっても良いかもしれない。といっても、信用されないとは思うのであるが...
 |
さて、先のTV番組によれば、腰からスカートの先までの長さを「スカートの丈」というらしい。また、先のTV番組により、「腰から下着の一番下の部分(股下を計るときの一番上)までの長さが大体25cmである」という重要な情報を得ることができた。
それでは、解析を始めてみよう。以下に、今回考えた「ミニスカートの幾何学」を示す。なお、今回使用する長さの単位は全て(cm )である。
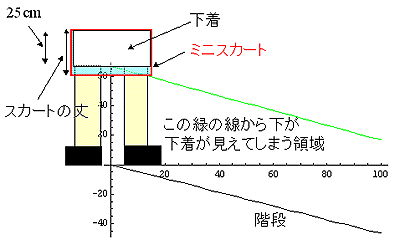 |
まず、階段の途中に立つミニスカートを履いた女性の下着中央部分とミニスカートの最下部を結ぶ直線を考える。この線よりも下が、下着が見えてしまう領域である。もちろん、階段の下には潜り込めないわけであるから、その線と階段で囲まれた領域内から見た際に下着が見えてしまうわけだ。その線のことを「下着防御ライン」と呼ぶことにする。
さて、ミニスカートの形状を考えよう、スカートの丈はもちろん入力条件としてわかる。すると、足りないパラメータは幅である。そこで、ヒップ周りが88cmとしてスカート中央から端までの長さ(rcm)を求める。2πrが88cmであるから、
r = 14cmとなる。
また、駅などの階段というと25度位だろうか。30度というとかなり急な階段である。湘南通商の階段とか急な階段は色々あるが、今回は急な階段の斜度として、25-30度位としておく。ちなみに、京都駅北口のエスカレータで実測したところ、25,6度であった。
それでは、スカートの丈が32cmで階段の角度が30度である場合の計算をしてみる。女性の股下は仮に70cmであるとしておく。おそらく、身長160cm位であれば、この程度であろう。
それでは、ミニスカートの丈が32cm、30cmの時の「下着防御ライン」を計算したものを示す。
 |  |
緑、すなわち、ミニスカートの丈が32cmの時は「下着防御ライン」は階段とほぼ平行である。それに対して、丈が30cmの時の「下着防御ライン」は、ミニスカートを履いた女性から離れるほど階段よりも上に離れていく。ということは、人間の視点位置が「下着防御ライン」を越えるということである。すなわち、下着が見られてしまうということだ。
階段と「下着防御ライン」の差、すなわち、人の目の高さがこの程度ならミニスカートの下の下着を見ることができる、というものを示してみる。
 |
32cmの丈の場合、10m(1000cm)離れても、目の高さが150以下の人しか「下着防御ライン」を突破できない。すなわち、女性は事実上「下着を見られる恐れがない」といって良いだろう。もちろん、20mとか離れたら別である。しかし、超人的な視力がなければ、そのような条件下で下着を確認することはできないであろう。
それに対して、30cmの丈の場合には6m離れた時点ですでに視点が2mの位置にある人でも「下着防御ライン」を突破できてしまう。これでは、「全ての人に下着を見られてしまう」ということになる。
もし、女性の身長が20cm程度高く、180cm程度であったら、どうなるだろうか。おそらく、股下長さは10cm程度長くなる。すると、上の図(階段と「下着防御ライン」の差)の緑、赤ラインは10cm程度高くなる。それでも、緑の32cmスカートの「下着防御ライン」はやはり安全圏といえるだろう。
また同様に、厚底サンダル・ブーツなどを履いた場合には股下長さが20cm弱高くなると考えられる。この影響を考えると、長さとしては身長の影響よりも大きいわけである。それは、身長の1/2が股下長さの増加に繋がるのに対し、厚底靴の長さはそのものずばり股下長さの増加に繋がるからである。しかし、それでもやはり緑の32cmの「下着防御ライン」は安全圏である。
すなわち、32cmと30cmのスカートの丈の長さの間には、「下着が見える・見えない」に関する分水嶺が確かに存在するのだ。先の、
「30cmだと下着が見えちゃうしぃ。」という発言は理論的に裏付けられたのである。
それでは、次に階段の角度が25度である場合の計算をしてみる。
 |
緑の線、すなわちスカートの丈が32cmの場合の「下着防御ライン」が階段にどんどんすり寄っているのがわかると思う。すなわち、「下着防御ライン」はより強固なモノとなっているのである。階段と「下着防御ライン」が女性から離れるほど近づくのである。次に、階段と「下着防御ライン」の差を見てみよう。
 |
緑線、すなわちスカートの丈が32cmの場合に注目する。 女性から、離れても、近づいても、何人たりとも、下着を見ることはできないのだ。下着がシュバルツシルト半径の中に隠されるといっても良い。女性の安全を確保する「完全安全条件」を満たす「下着防御ライン」が完成されているのだ。
これは階段と「下着防御ライン」が平行である条件を境として、そのような条件が達成される。その条件よりより「下着防御ライン」が強固になると、誰も「下着防御ライン」を突破することはできない。すなわち、「完全安全条件」が達成されるのである。
この絶対に下着を防御可能(「完全安全条件」)な「完全安全条件」とは、階段と「下着防御ライン」が平行である条件であるから、ミニスカートの丈(xcm)をパラメータとして、
Tan[階段の角度] = (x-25)/14で計算することができる。ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である。もちろん、極端な安産体型の場合には、その14という値を適当に補正する必要がある。
さて、この条件には女性の身長(股下長さ)は関係しないところが面白い。もちろん、厚底サンダルなどを履いても同じである。もちろん、若干の影響はあるが、あまり影響はない。
さて、今回の「ミニスカートの幾何学」の考察により、判明した結果をまとめてみよう。
ミニスカート内部の下着が「見える・見えない」には
- ミニスカートの丈が30cmと32cmの間に、分水嶺が確かに存在する
- 絶対に下着を防御可能(「完全安全条件」)なミニスカートの丈(x cm)とは、Tan[階段の角度]= (x-25)/14 により決定される
- ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である
- 極端な安産体型の場合には、その14という値を適当に補正する必要がある
- 一方、ミニスカートを履いている人の身長はほとんど影響を及ぼさない
- 厚底サンダルの方が身長よりは影響を及ぼすが、それでもほとんど影響はない
ミニスカートを身につける女性の経験に基づく、「30cmだと下着が見えちゃうしぃ。」理論はなかなか正しいことがわかる。経験というものを軽んじてはいけない、という良い?例かもしれない。結果の伴わない理論に価値はない、ということだろうか。
それにしても、厚底ブーツにミニスカートを履いた女性達は、ロールプレイングゲームの主人公達のようだ。色々なアイテムを手に入れ、冒険を続けている主人公達のようである。ほんの少しだけ、うらやましいような気もする。
さて、こういう話題を書くと少し不安がある。もちろん、私もミニスカートを見ると、妙に心が落ち着かないのも確かに事実ではある。しかし、だからといってことさらに興味津々というわけでもない、と思う。多分。ということで、「できるかな?」の女性読者の数が減少しないことを、ただ祈るのみである。
2000-08-11[n年前へ]
■明日から夏休み 
「日常から脱して、スリルと冒険があって、新しい何かが見つけられる... そういったものを探してこそ、いや探そうとする心こそ本当のバカンスではないでしょうか」 金子修介 from 朝日新聞 8/11
2001-10-20[n年前へ]
■トリック comes back 
えー、私、天才奇術師の山田奈緒子です。ひさしぶりだな。 「トリック」の放送終了から一年経ちました。お客様から「奈緒子さんの華麗な冒険をまた観たい」という声を沢山のハガキや伝書鳩でもらったので 「トリック2」 ってことで、またやります。でも12月までは奇術師にとっては稼ぎ時なので、来年の1月からやることにしました。
(リンク)
2002-07-07[n年前へ]
■ぼくのなつやすみ2 海の冒険篇 
十年くらい前のJR東海の夏のCMがハックルベリー・エクスプレス。「それでさぁ、海は石垣のムコウだよね?違うよ、海は松林の先だよ。」このシーンではいつも涙が出そうになった。
きっとゲームはしないけど、7/11には買ってみよう。(リンク)
2002-08-04[n年前へ]
■キラキラ光る景色を描く 
「木漏れ日」プラグイン「リン」を作る
夏の休日には、朝早く起きて西伊豆の松崎の先にある「雲見・岩地・石部」辺りへ行って、海の中でお魚と戯れてみたり、海辺の温泉に長々とつかってみたりする。例え休日であっても朝早く行けば混雑とは無縁だし、海に照りつける太陽と温泉とビールの三点セットが揃えば、夏の景色としてはとても素敵なのである。
とはいえ、今日は朝寝坊したので、松崎までは行かずに「無名だけれどとても良い感じの場所」へ行った。海辺に車を止めて、景色を眺めて、ほんの少しの時間泳いでみた。下はその西伊豆の某所で眺めた「今日見た景色」だ。
 「雲見、岩地、石部」であれば温泉も海も最高だけれど、西伊豆の辺りには他にも「海水が綺麗で、人も全然いなくて、トイレも水もある」ような場所はいくつもある。これはそんな場所の一つ。 県道から海辺の集落に向かう道沿いには素晴らしい滝もあって、まるでプレイステーション2のゲームソフト「ぼくのなつやすみ2海の冒険篇」の世界に迷い込んだかのよう。 実際に眺めていた景色はもっとキラキラしていたハズなのに、その片鱗も残っていない…。それはひとえに写真を撮ったワタシのウデが悪いから。 |
海辺でワタシが実際に眺めていた景色は、もっとずっと「キラキラ」していたハズなのに、残念なことに上の写真を眺めてみても、その片鱗すら残っていない。揺れてる波間も、足下の濡れている岩も、眩しい太陽だってもっとずっとキラキラしていたハズなのに、上の写真はただボンヤリした写真になってしまっている。それは、ひとえに写真を撮ったワタシのウデが悪いからである。もちろん、それが一番の理由である。クヤシイ話ではあるが、確かにワタシのウデは悪いのである。
とはいえ、言い訳を少しばかり書くならば、実際に眺めていた景色がもっとずっとキラキラしていた理由は他にも考えられる。例えば、ワタシ達が景色を眺めるときには、目の前にかかる髪の毛や、睫毛や、目の水晶体を通して景色を眺めているわけで、それらの中で光が回折したりして、キラキラとまるで虹のように光が輝いて見えたりするからだ。そのため、例えば夜空の星の形、本来は丸いはずの星の形、が星型に見えたり、木漏れ日が虹のように輝いて見えたりする。
そんな様子をもしカメラで再現しようとするならば、ケンコーが出しているクロスフィルターのようなものをつけることになる。しかし、手軽さが取り柄のデジタルカメラでわざわざそんなフィルターをつけるのは面倒くさいし、第一人によって見え方は違うから、「ただ一つのフィルター」で写真を撮ってしまうのは少しばかりイヤな気がする。例えば、「私は目の前に髪の毛がたくさんかかってしまって邪魔なのー」という人もいれば、「最近、抜け毛がハゲしーなぁ…、目の前に髪の毛がたくさんかかっていたあの頃が懐かしぃ…」という人もいるわけで、そんな二人が眺めた景色はきっと全然違うハズなのである。「百人の人がいれば百人百葉様の景色を眺めている」わけで、写真を撮る時点でただ一つのフィルターをデジカメにはめて写真を撮ってしまうのも面白くない。フィルターに限らず、何事も一つの枠にはめてしまうのは良くないのである。
デジカメの便利なところは、何より撮った後の画像加工が自由自在、というところなわけで、撮った後に「眺めた景色」を再現するように画像を加工してやれば、「写真を撮るときには素直な景色を撮って」「その後で自分が眺めたキラキラ光る景色を蘇らせる」ということができる。そこで、今回はそんな「キラキラ光る景色を描く」Photoshop用のプラグインを作ってみることにした。そして、ワタシの写真の腕の悪さを「技術の力」で誤魔化そうと思うのである。
といっても、基本的には、「ボケ」た背景で包み込めの時の処理を基にして、
- 色々な畳み込みの演算カーネル形状を用意し
- 演算カーネルのサイズを強度やアルファチャンネルの情報を元にしてピクセル単位で可変にし
- カーネル演算を対数変換有無などに対応する
RINgの出力サンプルを少し眺めてみると、下の画像のようになる。まず最初のサンプル画像は、クローバーの写真に「虹十字状」の畳み込みの演算カーネルを用いて、処理をしてみたものだ。左のオリジナル画像では、朝露を載せて光るクローバーを眺めるときに私達が感じる「キラキラしたようす」がほとんど写っていないが、右のフィルター後の写真では私達が睫毛などを通して景色を見るときに感じる虹色のキラキラした自然?な景色が映し出されている。
| (畳み込みの演算カーネルは虹十字状)  |
そして、また下の写真は、新宿から初台へ歩く途中で眺めた木漏れ日の向こうのビルの景色だ。左のオリジナル写真はクッキリ・ハッキリ写っているのだが、ただ「それだけ」である。太陽の光を遮る木々の葉っぱも、そこから降り注ぐキラキラする木漏れ日も写ってはいない。しかし、右のRINgが描いた景色の方では、ボンヤリと、だけど強く光る初夏の「木漏れ日」が確かに写っているのである。夏の空気が写っているかのようなのだ。
| (畳み込みの演算カーネルは円状)  |
もちろん、このRINgは「ボケ」た背景で包み込めの時の処理を基にしているので、写真のボケも再現することができる。例えば、六角形の畳み込みの演算カーネルを用いて、画面全体に同じ演算カーネルで処理をかけると下の右の写真のようにピンボケの写真を再現することができる。
 |  |
また、アルファチャンネルも選択してフィルタ処理を行うと、自動的にアルファチャンネルの情報を基に畳み込みの演算カーネルサイズを画素毎に変化させる。だから、例えばアルファチャンネルに距離の情報を入れておいてやれば、下の写真のように距離に応じたボケなども再現することができる。この写真では画面中央下の領域はピントが合ってていて、そこから離れるに従って、ピンボケの具合が大きくなっている。もっとも、現在のバージョンでは大雑把に計算してみただけなので、空の部分などに疑似輪郭などがずいぶんと発生してしまっている。きっと、それはいつかのバージョンで直すつもりなのである。
 | (畳み込みの演算カーネルは円状)  |
今回のRINgプラグインは光が広がる様子を保存した「畳み込みの演算カーネル」を基に画像にフィルタをかけるだけなので、使う演算カーネルの形状・様子によって色んなフィルタに早変わりする。
例えば、デフォルトでつけてある三日月型の"Moon"カーネルを使えば、色んな灯りが三日月型に光る景色に早変わりする。もし、星空の写真に"Moon"カーネルでRINgプラグインをかけたら、いきなり全ての星が三日月に早変わりだ。また、"Smile"カーネルであれば、いきなり光が大小様々な「笑顔」に早変わりする。そんな風にして、色んな画像ファイルを演算カーネルにして見ると、色んな景色が見えてくるはずだ。例えば、「星はなぜ星型に見えるのか」のグループが作成した「星型シミュレーションソフトウェア」の出力結果を演算カーネルにすれば、目の前の景色が星空の向こうの景色に早変わりするだろう。そしてまた、水で満たしたコップの向こうに浮かぶ光の画像を使えば、RINgはデジカメで撮った色々な写真を水槽の向こうの景色であるかのように描き直したりするかもしれないし、あるいはまたまるで瞳に涙を浮かべながら景色を眺めてみたかのように描き直したりするかもしれない。

