hirax.net::Keywords::「宝石」のブログ

■私と二度めに出会う「水」　

クリスマスの小さな遺品

　先日、こんなメールを頂いた。

　私の娘は小学三年生。図書館から借りてきた「水の一生」といった、子供向け科学本（蛇口から出た水は下水を通って…<途中大幅に省略>…再度雨になって…というヤツです）を読んでおりました。そこで彼女はいくつかの疑問を口にしました。

「一度下水に流した水は、どのくらい経ったらまた私のところへ戻ってくるの？」
 

私　「必ずしもすべての水が海まで行くわけではなくて、下水処理場で蒸発して、川の取水口あたりで雨になる分子もあるはずだから、そうだなあ、一番早くて３日くらいかなあ。　勿論もっと長い場合もあるし、一度流したらキミが生きている間にはここには戻ってこない分子もあると思うよ」

「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」

私　「う〜ん…　　どれくらいなんだろう？」

　さて、どう思われますか？

　ところで、この後半の疑問「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」というのはたまに見かける話である。何かの小説で、「このコップの話が主人公が科学を志したきっかけになっている」という小道具に使われている例も読んだことがあるような気がする。

　たまに見かける話ではあるのだけれど、同じ本を読んでも人それぞれ抱く感想は違うし、私なりにも考えてみたい気もしたので、今回はこの「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」を考えてみることにした。

　人が一日に「出会う」水はどの位の量だろうか？成人男子が安静にした状態で、一日当たり大体2.5リットルの水を消費するという。すると、小さい子供の場合でも、少なくとも一日2リットルくらいは水を消費する、つまり水と「出会って」そして「分かれる」ことになる。2リットルの水というと、2000gだから、これを水の1molあたりの重さ18g /molで割って、さらにアボガドロ数（1mol当たりの分子数）をかけてやると、(2l = 2000g ) / 18g x 6.022x10²³個 = 6.7 x 10²⁵個となり、私たちが一日に出会う水分子の数の個数がわかる。

　この「とある一日に私たちが出会った水」が川へ流れて、海へ流れて、地球上にまんべんなく拡がったとしよう。地球上の限りなくある水の中に含まれる「とある一日に私たちが出会った水分子」の割合は、いったいどのくらいの程度になるのだろうか？

　地球上の水は大体14億km³くらいだという。そのほとんどは96.5%は海水で、残りが陸地のさまざまな場所（そしてわずかに空気中）に存在している。この地球上にある水の重さを計算すると、14億km³= 1350000000km³ = 1.4 x 10⁹ x 10¹² kg= 1.4 x 10²⁴ g ということになって、これを水の1molあたりの重さ18g /molで割ってやると、地球上に存在する水分子の総量は 1.4 x 10²⁴/ 18 = 7.8 x 10²²mol ということになる。mol数から水分子の量に直すために、アボガドロ数6.022x10²³個/molをかけてやると、地球上の水分子の総量= 4.5 x 10⁴⁶ 個という数字が得られる。

　すると、地球上の限りなくある水の中に含まれる「とある一日に私たちが出会った水分子」の割合は
「とある一日に私たちが出会った水分子」 / 地球上の水分子の総量 = 6.7x 10²⁵個 / 4.5 x 10⁴⁶ 個 = 1.5 x 10^-21= 0.00000000000000000015%というとても小さい割合になる。この割合は、新たに水分子と出会った時に、その水分子が「とある一日に私たちが出会った水」である確率と言い換えても良いだろう。とにかく、私たちの普段の生活の感覚からすれば、限りなく小さく思えてしまう。しかし、その再会の確率はとても小さく思えてしまうのだけれど、決して私たちは「とある一日に私たちが出会った水分子二度と水と再会しない」わけでは無いのである。

　例えば、180mlのコップ一杯の水の中には( 180ml = 180g ) / 18g x 6.022x10²³個= 6.0 x 10²⁴個の水分子が含まれている。ということは、このコップ一杯に含まれる水分子の中にいる、かつて「とある一日に私たちが出会った水分子」の数を計算してみると、
コップ一杯に含まれる水分子の数 x 「とある一日に私たちが出会った水」である確率= 6.0 x 10²⁴個 x 1.5 x 10^-21  = 9000個ということになる。コップ一杯の水の中にはかつて「とある一日に私たちが出会った水」が一万個近くも存在していることになる。

　しかも、この計算は「とある一日に私たちが出会った水分子」だけで計算していて、決して「これまでに私たちが出会った水分子」で計算しているわけではないのだから、「コップ一杯の水の中で、私と２度目に出会う水」はもっと多いことになる。もちろん、実際には私たちが消費した水が理想的に拡散したりはしないだろうから、こんな風に上手くはいかないだろうけれども。

　とりあえず、「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」という疑問を口にした小学校三年生の娘さんには、「ずっと昔のある日に出会った水がコップ一杯の中には一万個近くもあるかもね」と答えておくのが良いかもしれない。計算の中身、アボガドロ数なんて言っても、小学校三年生では「あぼがど？あぼがろど…？」と頭がこんがらがるだけかもしれないけれど、とりあえず「おとーさんって、何でもわかるんだー」とちょっとくらいは尊敬されたりするかもしれない。
 

　そういえば、先日東京で初雪が降った。「雪は天から送られた手紙」とは中谷宇吉郎の残した名言だけど、その雪を見ながらこんなことを考えた。

　ある日誰かが亡くなり、荼毘に付される。すると、その人の体のほとんどの部分は火と共に空へ昇っていくことだろう。成人の体のおよそ60%は水分だから、体重60kgの人であれば、その60%の36000gもの水が空へ還ってゆくことになる。その空へ還っていった水分子が世界中に散らばっていった後に、いつかまたその水分子と出会うためにはどの程度の水があれば良いだろうか？どの程度の水があれば、この中には「かつてあの人と共に空に帰っていった水分子」が一個くらいはある、と言えるものだろうか？

　これを先程と同じように計算してみると、ほんのちょっと「1 x 10^-3g」ほどの水があれば、その中には「かつてあの人と共に空に帰っていった水分子」が一個くらいある、という結果になる。「1x 10^-3g」ということは、大きさで言うと1mm³ほどになる。ちょうど雨粒一滴と同じ位の大きさだ。空から降ってくる雨一粒の中には「かつて亡くなった人と共に空に帰っていった水分子」が１個が漂っている、ということになる。

　冬の雪の一片の大きさが雨の一粒と同じくらいであるかは判らないけれど、今日のように何時の間にか雨が雪に変わることもあるくらいだから、やっぱり雪も雨と同じような大きさなのだろう。だとすれば、空から降ってくる雪の一片の中には、「かつて亡くなった人と共に空に帰っていった水分子」が１個宝石のように入っていてもおかしくはない。「雪は天から送られた手紙」であるならば、その中にはその手紙を天から送ってくる「かつて亡くなった人」のまるで遺品が１個づつ封じ込められているのである。「雪は天からの遺品」と言っても良いかもしれない。

　間もなく、クリスマス。そして、クリスマスには白い雪が付き物だ。空から舞い降りてくる白い雪の中には大切な１個の水分子「クリスマスの小さな遺品」が入っているのである。

■銀玉鉄砲を撃ちまくれ。(前編)　

銀玉鉄砲の弾道計算

 　世の中には「似て非なるモノ」が溢れている。一見同じように見えるのに、よく見ると何故だか大違いというものである。そしてまた、その「似て非なるモノ」の亜種として「言葉の上ではよく似ていて、実際のところもやっっぱりよく似ているのに、世間一般での印象が全く異なるモノ」というのが数多くある。

　その一例が、「月光仮面」と「けっこう仮面だ。月光仮面は「月よりの使者」をキャッチフレーズにする正義の味方で、けっこう仮面は「愛と正義の使者」をキャッチフレーズにするやはり正義の味方だ。二人ともマスクをかぶった正義の味方だし、そのキャッチフレーズだって互いによく似ているのに、世間一般の印象は大違いなのである。「昔、私は月光仮面に憧れていてね～」と遠い目で語る男を優しく見守る女性はいるかもしれないが、「なんてったって、も～、オレはけっこう仮面が好きで好きで～」と呟く男を優しく見守る女性はいるわけはないのである。同じように思い出を語っているのに、そしてその響きもほとんど同じなのに、世間の印象というのは全然違うモノなのである。「月光仮面」と「けっこう仮面」は「似て非なるモノ」なのだ。

　そして、よく似た「似て非なるモノ」がもう一つある。それは銀玉と金玉である。両者ともに「金銀銅」というフレーズで並び称される「貴金属の名」に「宝石を意味する玉」が付け加えられたものであり、ギンダマという響きとキンタマという響きだってそっくりであるのに、その響きを人前で発っした場合の印象は180度違うのである。いや、実際のところはギンダマと口から発することはできたとしても、キンタマなんて口から言葉を出すことは普通一般的にはできないのである。口に出すだけでなくて、例えば恋人を部屋に呼んで、昔のおもちゃ箱を開けながら「ホラ、オレの銀玉鉄砲ー、懐かしいだろー」なんて見せびらかせば、「まだコドモみたいー、可愛いー」となるかもしれない。ところが、同じように恋人を部屋に呼んでも、「ホラ、オレの金玉鉄砲ー、スゴイだろー」なんてキンタマテッポーを見せびらかした日には、これはもう一体どうなることかわかったものではないのである。その響きも、そしてそのピストルとしての役割も、銀玉鉄砲と金玉鉄砲はよく似てはいても、その二つはやはり「似て非なるモノ」なのである。
 

　そんな「似て非なるモノ」の片割れの「銀玉鉄砲」、生まれてはや50年ほどになる銀玉鉄砲を、昨日散歩の途中に買ってしまった。街中を歩いていると、古びたオモチャ屋が人知れずあって、その店に気づいたワタシはついつい足を踏み入れてしまったのである。そして、その店の中で棚の下の段ボールに入っていた銀玉鉄砲を見かけたワタシは、思わず銀玉鉄砲一セットを買ってしまったのである。銀玉鉄砲150円＋玉100円のしめて250円ナリであった。玉は残念ながら銀玉ではなくて、BB弾だったのだけれども、少なくとも安っぽい銀玉鉄砲の方は昔と同じ見てくれだった。
 

　「銀玉鉄砲の昔」で思い出すことといえば、子供の頃に遊んだ銀玉鉄砲を武器にした「撃ち合い遊び」だ。あの遊びのことをなんと呼んでいたのかはもう覚えていないのだけれど、きっと適当に「戦争ごっこ」とでも称していたのだったと思う。やっていることは同じでも、それを今風に「サバゲ」などと呼んでしまうとそれは「アレゲ」（＝「何だか、ちょっと言い難いけど、アレっぽいよねー」という程度の曖昧な言葉）な世界になってしまう。だから、やはりここは銀玉鉄砲で「戦争ごっこ」くらいの言い方にしておくと、その「戦争ごっこ」で使われる銀玉鉄砲の射程距離は子供心にもそんなに長くなかったような気がする。確か、かなりの至近距離でバンバンと撃ち合っていたような気もするし、少なくとも狙う相手が見えないような遠くから撃つものではなかった。それに、映画の「マトリックス」の一シーンではないけれど、自分を狙って撃った弾を何とか避けたりすることも（たまには）できたりしたような気がするから、きっと銀玉はヒョロヒョロの弾道を描いていたのだと思う。
 

　「できるかな?」では、以前「似て非なるモノ」の片割れ＝金玉鉄砲の弾道計算をしたことがあった。その名前の響きも、その役割もほとんど同じ「似て非なるモノ＝キンタマテッポー」の弾道計算をしたのであれば、せっかくだから今回はもう片方の「似て非なるモノ」＝銀玉鉄砲の弾道計算をしてみることにしようと思う。
 

　まず、銀玉鉄砲で発射された銀玉の初速度（≒10m/s）と、銀玉の重さ（≒0.2g）というデータと、銀玉の直径が6mm強というデータを元にまずは銀玉の弾道を計算してみた。下のグラフは「無風状態で銀玉鉄砲を1.2mの高さで水平方向に銀玉を発射してみた時の銀玉の弾道」を示している。下に示した二つのグラフの中で、上のグラフは「空気抵抗を考慮した場合」であり、下のグラフの方は「空気抵抗を考慮しない場合」である。
 

銀玉鉄砲とエアガンの弾道（玉の重さ=0.2gの場合）

空気抵抗を考慮した場合

空気抵抗を無視した場合

　空気抵抗を無視すると、昔使っていた銀玉鉄砲の銀玉は7m程飛ぶことになる。しかし、実際には銀玉に空気抵抗が働くために、飛距離はそれより少しだけ短くなって6m程しか飛ばないことになる。とはいえ、空気抵抗のせいで短くなってしまった距離は高々1m程なわけで、実際のところ昔の銀玉鉄砲では空気抵抗はあまり影響していなかったのである。子供の頃の記憶を呼び起こしてみても、実際に銀玉はそんなに遠くまで飛んでいるわけではなかったし、この計算結果でも飛距離6mというと「十分遠く」まで飛んでいるとはいえなかった。だから、銀玉鉄砲のバネを改造して強くしてみたり、あるいは銀玉の重さを変えてみたりして、銀玉を遠くまで飛ばそうとした記憶がワタシにはある。その記憶に沿って、「銀玉鉄砲の銀玉の重さを変えてみた場合に銀玉の弾道がどう変わるか」を計算してみたのが下の三つのグラフである。
 

銀玉鉄砲の銀玉の重さを変えてみた

銀玉の重さ = 0.1g

銀玉の重さ = 0.2g

銀玉の重さ = 0.3g

　上のグラフを眺めてみれば、「銀玉の重さ」を軽くすると銀玉鉄砲の銀玉の飛距離はわずかながら長くなることがわかる。子供だった頃を思いおこしてみると、子供心に「銀玉の重さを軽くすると、遠くまで飛ぶハズ」という程度の曖昧な確信で改造をしていたような気がするけれど、アレは今考えてみても正しかったのだなぁ、と思うのである。もちろん、今では「銀玉鉄砲のバネのエネルギーが銀玉の運動エネルギーに変わるから、銀玉の重さの逆数のルートに比例して銀玉の初速度は速くなる。だから、空気抵抗が無視できる場合には銀玉が軽ければ遠くまで飛ぶ」と自然に考えるわけだけれど、少なくとも昔はそんなに淡々とは考えはしなかったのである。
 

　さてさて、そんな懐かしい気分から今現在に気分を強引に取り戻して、最近巷に溢れているという強力なエアガンと昔の銀玉鉄砲の弾道を比較してみたのが下のグラフだ。昔の銀玉鉄砲より50倍ものエネルギーがある最近の強力なエアガンの場合である。そんなエアガンでは、なんと銀弾鉄砲の5倍近く25m以上もの飛距離がある。現実の兵器の世界でも性能競争が激しく行われているのと同じように、おもちゃの玩具の兵器開発も激しいようだ。5mと25mでは大違い、まさに飛び道具である。ここまでくるとやはり「玉」ではなくて「弾」と書く方がふさわしいように思えてしまう。
 

銀玉鉄砲(初速エネルギー=0.02J)と
エアガン(初速エネルギー=1J)の弾道（玉の重さ=0.2gの場合）

　そして、ここまで強力になってしまうと、その特性も昔の銀玉鉄砲とは全くの別物になってしまう。その証拠に、先ほどの銀弾鉄砲の場合と同じように「発射する弾の重さを変えてみた場合の弾道」を計算してみたものを下に示してみよう。なんと、最近の強力なエアガンの場合は、弾の重さを重くすれば重くするほど遠くまで飛ぶのである。昔懐かしの銀弾鉄砲が銀玉を軽くすればするほど遠くまで飛んだのとは全く逆なのである。最近のエアガンのパワーがあまりに強力で弾の発射速度が速いために、空気抵抗による影響が支配的になってしまうのである。そのため、弾の重さが軽い割に直径が大きい弾よりも、重さの割に直径が小さい弾の方が遠くまで飛ぶようになる。
 

強力な(1J)エアガンで銃弾を撃った場合の弾道

弾の重さ = 0.1g

弾の重さ = 0.2g

弾の重さ = 0.3g

　こんな風に、昔の子供のおもちゃ銀玉鉄砲と最近の強力なエアガンはパワーがあまりに違うため、結局のところその特性は「似て非なるモノ」になってしまっている。「姿形はよく似ているのに、その特質をよく見てみると少し違っていて、その印象は結構異なるモノ」になってしまっている。単にパワーの大きさが違うだけで、そんな特性・印象の違いが生まれてしまったりする。子供と大人が大きさとほんの少しの特質が違うだけで結構違う（部分もある）のと同じなのである。

　そう、例えて言うなら銀玉鉄砲は「子供のおもちゃ」でエアガンは「大人のおもちゃ」なのだ。「言葉の上ではよく似ていて、実際のところもやっっぱりよく似ているのに、世間一般での印象が全く異なるモノ」になってしまっているのである。まさに、ギンダマテッポーは「子供のおもちゃ」でキンタマテッポーは「大人のおもちゃ」だったのである。そんなことを考えると、「昨日ワタシが散歩の途中に買ってしまった」のがギンダマテッポーで良かったなぁ、とつくづく思うのである。だって、「ワタシは散歩の途中に「大人のオモチャ屋」にふと足を踏み入れて、大人のおもちゃを買ってしまったのである」なんて言葉を聞く世間の印象はずいぶんと違うに違いないのだから。

■世界を映す玉手箱　

掌の上の不思議な世界

　先日、人工衛星から撮影された夜の地球を眺めてみた。そんな夜の地球で輝いている「街の灯」を眺めていると、そんな宝石のような地球を自分の掌の上に載せて眺めてみたくなる。夜の「街の灯」できらめいていたり、人が住んでいるのに真っ暗だったりする、そんな小さな地球を作ってぼんやりと眺めてみたくなる。

　そういえば、一年近く前に「小さな掌に未来の地球儀をのせて」でメルカトル図法の地図画像から正二十面体展開図を作成して、小さな正二十面体の地球儀を出力するソフトウェア"Icosahedron"を作ったことがあった。このソフトとプリンターがあれば、色んな地図から掌に載る小さな地球を作ることができる。そして、自分の掌の上で小さな「夜の地球」を眺めてみることができる。
 

"Icosahedron"で作った「小さな正二十面体の地球儀」

　そういうわけで、夜の地球の画像を"Icosahedron"で読み込んで「小さな正二十面体の地球」を作ってみたのだけれど、その作業の途中で"Icosahedron"をいじって、

• うっかりミスのバグ修正（メルカトル→正二十面体展開図変換が間違っていた）
• のりしろ部分をきちんと描くようにした
• ソフトから直接印刷もできるようにした
• Susieプラグインに対応

正二十面体展開図作成ソフト"Icosahedron"の動作画面

Loadボタン　→　メルカトル図法で描かれた画像ファイルを読み込む  Resizeボタン　→　作成する正二十面体のサイズを決める。プリンタでの出力解像度、正二十面体の直径を決める。  Convertボタン　→　正二十面体の展開図を作成する  Saveボタン　→　Windows Bitmapファイルとして正二十面体の展開図を保存する  Printボタン　→　プリンタで印刷する

• Icosahedron (2002.1026) Windows版  429kB(Linux版公開時のお知らせは"いろいろ"の方で…)

　ところで、地球を中心にして地球を全周囲から眺めた様子を二次元に投影したものが地図だけれど、その全く逆のことをしたものがある。それはパノラマ写真である。何故なら、パノラマ写真は「世界の何処か一点を中心として、その点から全周囲を眺めた様子を二次元に投影したもの」であるからだ。つまり、「何処かを周囲から写したものが地図」で「何処かから周囲を写したものがパノラマ写真」であるという違いだけで、その二つはほとんど同じものだ。だから、パノラマ写真を元にして、Icosahedronで正二十面体を作ってみても、ちゃんとした世界ができあがる。

　例えば、パノラマ写真を元にして、"Icosahedron"で「とても巨大な正二十面体の展開図」を作って、景色が印刷された面を内側にして「人が入れるほどの巨大な正二十面体」を作ってみれば、それは即席のパノラマ上映館となる。そしてまた、逆に景色が印刷された面を内側にして「小さな正二十面体の展開図」を作って組み立ててみれば、それは周囲を全ての景色をまるで鏡のように映し出す不思議な水晶玉のようなものができあがることになる。外に向かって「何処かから見た外側の景色」を映し出す不思議な水晶玉ができあがることになる。

　結局のところ、数学的に言えば「巨大なパノラマ館」と「小さな水晶玉」の違いは曲率の符号が反対、というだけである。「巨大なパノラマ館」の場合は曲率がプラスで「世界が閉じて」いて、「小さな水晶玉」の場合は曲率がマイナスで「世界が開いて」いて、そして「正二十面体の展開図」の場合は曲率が0で「世界が平坦」だというだけの違いにすぎない。だから、「巨大なパノラマ館」はその中に向かって「何処かから見た外側の景色」を上映しているけれど、「小さな水晶玉」の場合はその外側に向かって「何処かから見た外側の景色」を上映している、ということになる。「巨大なパノラマ館」を"insideout"にひっくり返してみれば、世界が開かれた「小さな水晶玉」に変身するというだけだ。
 

　以前、「箱根の湖尻から眺めた早朝の世界」をパノラマ写真にしたことがあったが、試しにこのパノラマの景色を映し出す小さな水晶玉を作ってみよう。
 

箱根の湖尻で眺めたパノラマの世界

　上の「箱根の湖尻から眺めた早朝の世界」を閉じこめた「小さな正二十面体」が下の展開図だ。これを組み立てさえすれば、小さな正二十面体の中に「ある場所から眺めた世界」が映し出されることになる。ちょうど、透き通った水晶玉を通して色々な場所からみた景色を眺めるように、この小さな正二十面体を覗けば「箱根の湖尻から眺めた早朝の世界」を眺めることができる。
 

眺めたパノラマの世界を小さな正二十面体に閉じこめた

　そしてまた、小さな正二十面体に閉じこめることができる世界はパノラマ写真に限らない。例えば、「自分の周囲を描いた絵画」であっても構わないだろうし、あるいは「自分が描いた何か」であっても良いと思う。そんなものを小さな水晶玉に閉じこめてみれば、その水晶玉は「自分の描いた世界」を外側に向かって映し出し始めるのである。

　例えば、エッシャーの「夜と昼」を正二十面体の世界に閉じこめてみたのが、下の展開図だ。これを組み立てれば、エッシャーの描いた世界が、エッシャーの描いた「昼と夜」が小さな正二十面体の中から映し出されることになる。これを組み立てた正二十面体を覗いてみれば、不思議なエッシャーの世界を色んな方向から眺めることができるのである。
 

エッシャーの世界を小さな正二十面体に閉じこめる
"Day and Night"

「エッシャーの昼と夜の世界」

　こんな風に、色んな画像から色んな「世界を映す玉手箱」を作ってみて、例えば「何処か旅先で撮った写真」や、例えば「誰かと撮った集合写真」や、例えば「自分の描いた落書き」や、色んな何かで小さな正二十面体を作ってみれば、きっと何か世界を写す小さな玉手箱ができあがると思う。その人だけの「その人の世界」を外に向かって映し出す小さな水晶玉ができあがるに違いない。正二十面体に閉じこめられた、だけど外に向かって開かれた、そんな世界を眺めてみるのはきっととても面白いことだろう。

　もしも、あなたがそんな小さな正二十面体を作ってみたなら、ぜひぜひその「世界を映した玉手箱」を写した写真を私にも送ってもらえるとうれしいです。そんな小さな世界の展覧会も開いてみたい、ですしね。

■Nothing but Echo　

水面に映る「私たち」

　「ニュースは世相を映す」とよく言われる。「世間で起きる出来事を伝えようとするもの」が「ニュース」なのだから、「ニュースが世相を映す」のは当たり前なのかもしれない。けれど、それだけでなく「ニュースは世の中の私たち自身を写している」ものだと思う。それは、世の中にいる誰かが「ニュース」を伝えようとするものである限り、その「ニュース」を受け取ろうとする私たちがいる限り、そのニュースは「私たち自身」を映し出すものだと思う。世の中にいる誰かが何かを伝えようとして、世の中にいる私たちがその何かを受け取ろうとしている限り、そのニュースは結局のところ「私たちの姿」を忠実に描き出すものだと思う。水面を上から覗きこんでみれば、その水面に景色だけでなく私たちの姿も同時に映りこんでいるように、ギリシャ神話のナルキッソスが泉の中に自分自身の姿を見たように、その「ニュース」には世の中の出来事だけでなく、私たち自身だって写りこんでいるに違いない。

　大林宣彦は朝日新聞「私の視点」の中で次のように語っていた。

「報道とは本来が客観的事実のみを伝えるものではなく、記者個人にとっての心の真実を伝えようと願うものであり、…　そしてまた、僕ら自身がメディアに何を求めているのかが、今問われている　…　僕らは、実は語る人間でもあるからだ。メディアもジャーナリズムも世論も僕ら自身であるからだ。」

　これはもちろん、「ニュース」の伝え手の役目も果たす２ちゃんねるだって同じだ。「名無しさん」という「誰でもない誰か」、だけど「世の中の何処かにいる誰か」の姿は結局のところ私たち自身の姿なのだと思う。だから、「２ちゃんねるは＊＊だ」という言葉は全て私たち自身に「私たちは＊＊だ」という言葉となって返ってくる。「２ちゃんねるはゴミだ」と口に出せば、それは「私たちはゴミだ」というエコーとなって返ってくる。もしも、「２ちゃんねるには宝石も埋まっている」というのであれば、「私たちの中には宝石も埋まっている」とそれは響くだけのことである。
 

　昨年末に放送されたNEWS23の 「あなたの物語」「誰でもない誰かの物語」では、視聴者の「テレビニュース」に対する意見をリアルタイムに募集しながら、その集まってくる答えを刻々とテロップとして流していた。「テレビニュース」が世の中に与える影響は？とか、「テレビニュース」はあなたの人生にとってなくてはならないものですか？とか、そんな質問への二択の答えの集計結果を刻々と流していた。その問いの中の、そして答えの中の「テレビニュース」の部分は全て「僕ら自身」と置き換えられるのだから、その最後の集計結果は全て自分達自身にエコーのように降りかかってくる。水面に映る「私たち自身が描く私たち自身の姿」を、恐る恐るそして祈りとともに覗いてみるのである。
 
 

■オンラインで遊ぶ「ダイヤモンド・デザイン」　

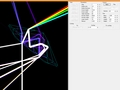　昔好きだったマンガが「パタリロ！」だった。このマンガの主人公はダイヤモンド産出国の国王だった。ダイヤモンドと言えば、ダイヤモンドのような宝石が好きな女性は多そうだが、ダイヤモンドのカットをデザインしたことがある女性は少ないかもしれない。
　このこのページでは、オンラインで「ダイヤモンドのカット・デザイン」をすることができる。ダイヤモンドのデザインをちょっと変えて、煌めきが失われたり、あるいはより輝いたりするようすを見れば、きっと面白いはず。そして、どの場所でどの色の光が煌めくかを眺めてみるのもきっと面白い。ダイヤモンドを身につけるのは好きだけど、その光学設計？をするのはキライなんていう人はこのページを見ていそうにないし、ね。