1998-12-27[n年前へ]
■Wveletで周期解析をしてみる 
音声・地震などの1次元信号や、画像等の2次元信号処理の解析というのはなかなか面白そうだ。そこで、周期ムラに対してWaveletをかけて周波数解析をする練習をやってみたい。また、短時間フーリエ変換とWaveletの比較もしてみたい。音声・地震などのデータはまた別にやってみることにして、今回は画像データを扱うことにする。ただし、いきなり2次元も何なので、画像データの周期(つまり1次元的な振動)に注目して、解析を行ってみたい。
まずは、「周期ムラのある画像」と「周期ムラのない画像」の2種類の画像を作成する。画像はいずれも数式を用いて作成した。X方向に変化する縞模様であり、表.1のような演算式になっている。一応、2次元画像ではあるが、Y方向にはなんの変化もない。2つの数式を見比べてみると判るが、いずれも2項からなり、低周波数のSinと高周波数のSinからなっている。「周波数ムラのある画像」では、その低周波数のSinの中にさらにSinがあるので、周波数がある周期で変化していることになる。一見、「周波数ムラのない画像」の方でも低周波数のSinの内部にさらにSinがあるように見えるが、0が掛けられているので、実際には存在しないのと同じである。
| 2つのSinからなり、その一方のSinの周期がムラ(一定の周期)をもっているもの。第二項目のSinの内部にさらにSinを入れることにより、周波数ムラを作っている。 | 2つのSin波からなり、どちらの周期も正確なもの。第二項目のSinの中のSinは0をかけてあるので、何ら影響を及ぼさない。 |
そのような数式に基づいて作成した画像を図.1に示す。なお縦軸がX軸であり、横軸がY軸である。図.2(b)では周波数ムラはないが、2つの周波数成分から作成されているため、うねりが生じている。
 | 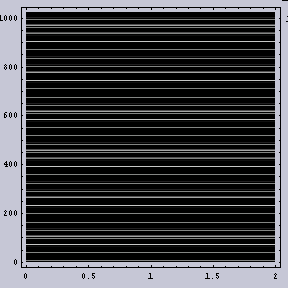 |
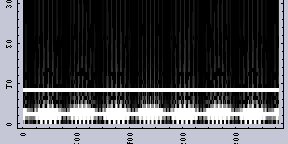
まずは、Wavelet変換である。図.2がその結果である。縦軸が周波数を示している。縦軸の上方向が高周波を示し、下方向が低周波を示している。また、横軸が原画像のX方向である。白は強度が小さいことを示し、黒は強度が強いことを示している。
いずれの画像も2つの周波数成分からなることが一目瞭然である。また、図.2(a):「周波数ムラのある画像」の方では低い周波数成分の方が、さらにある周期で周波数が変化していることがわかる。
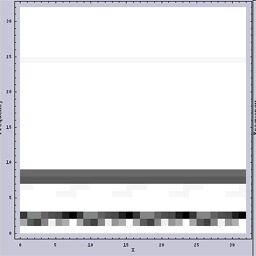 |  |
同じWavelet変換でも異なるFilterを用いてみると、結果は異なる。例えば、図.3がその例である。こちらの方が「周波数ムラ」がどのように生じているかを見るにはいいかもしれない。
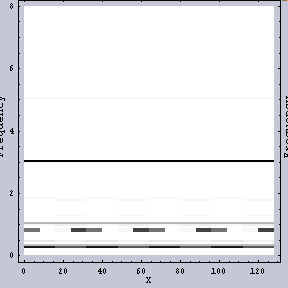 | 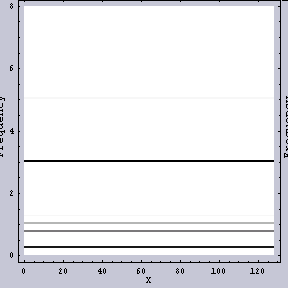 |
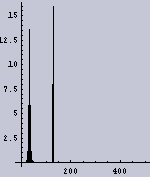
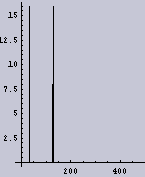
それでは、Wavelet変換ではなくて、フーリエ変換を用いて周波数解析を行ってみる。先ほどの1次元データの全領域に対してフーリエ変換をかけてみる。その結果が図.4である。ここで、横軸が周波数を示し、右側が高周波数を示し、左側が低周波数を示している。縦軸は強度である。
このフーリエ変換の場合も、2つの画像が2つの周波数成分からなり、図.4(a):「周波数ムラのある画像」では低周波数成分がぶれているのはわかる。しかし、その周波数ブレがどのようなものであるかまでは、わからない。
 |  |
なお、単純のためにウィンドー処理はしていない。そのために悪影響は当然出てしまう。
 |  |
単なる全領域にわたった周波数解析と、位置と周波数が同時にわかる解析の違いは非常に大きい。使いこなすのはなかなか難しそうだが....
1999-02-28[n年前へ]
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
 |  |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
 |  |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 |  1階微分 |
 13/10 (=1.3)階微分 |  15/10 (=1.5)階微分 |  17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
1999-10-18[n年前へ]
■沸点と数学の挑戦状 
みつからない「解決編」
| いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか? いつだって、どこでだって、謎はすぐ近くにあったのです。 何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。 加納朋子 ななつのこ より |
加納朋子の「ななつのこ」という小説を読んだ。創元推理文庫から出ているのだから、ミステリといっても良いだろう。私の好きな北村薫の「空飛ぶ馬」に始まる「円紫さんと私」シリーズによく似た雰囲気を持つ本である。
それを読んで、ふと思い出した。
私が通っていたM高校の話だ。M高校は武蔵野の玉川上水のほとりにある。
そのことを聞いたのは月曜の朝だ。日曜日の昼間に変質者が現れたというのである。目撃した人によれば、変質者は生徒用の上履きを履いていて、手には白い布を持っていたという。顔などはよくわからなかったそうだ。目撃者に驚いた変質者は逃げてしまい、白い布を落としていった、というのだ。
それだけなら、「単なる変な奴がいた」ということで話は終わった筈だ。問題は、その白い布に麻酔薬が含ませてあったという点だった。悪ふざけではすまない。
私は友人の鴨志田とその事件について話をしていた。気になることがあったからだ。変質者が目撃された場所が問題だったのだ。図に描くとこんな感じだ。
 |
 |
そこは2階の中では職員室から一番遠い。一番校門に近い玄関を揚がった所である。そして、生物室の隣だった。
生物室は、普通の教室とは違う。通常は鍵がかかっているし、それは鍵がかけられるということでもある。
生物部の部長・副部長は生物室の鍵を使える立場にあった。そして、鴨志田は生物部の部長だった。
「変質者は生物室に出入りできる奴かな?」これはどうにも重大な問題だったのである。
「生物の部長・副部長経験者ってこと?」
「うーん。」
「麻酔薬ってクロロホルムとか、かな?」と鴨志田にぼくが言うと、「立て板に水」状態で、彼の推論を聞かせてくれた。
「いや、きっとエーテルだね。」なるほど説得力はある。いや、ありすぎるといっても良い程だ。コイツ、むちゃくちゃ怪しいヤツである。犯人候補No.1である。一朝一夕で考えた理屈とは思えない。
「今時、クロロホルムなんて使われていないんだよ。」
「副作用もあるしさ。」
「あと、沸点を考えてみろよ。」
「エーテル、つまりジエチルエーテルDiethyl Ether ( (C2H5)2O )は沸点が34.6℃だ。」
「それに対して、クロロホルムChloroform ( CHCl3 )は沸点が61.7℃だ。」
「ハンカチにクロロホルムを含ませて顔に当ててもなにもおきない。」
「だけど、エーテルは人間の顔にあてたら、体温のせいで瞬間的に気化するんだよ。」
「つまり、エーテルの気体で顔の周りが覆われるわけだ。」
「呼吸なんかしたらエーテルを吸わざるをえないだろ。」
「だから、クロロホルムとかよりエーテルのほうが、変な用途には向いているんじゃないかな。」
「もっとも、即座に気を失うとは思えないけどね。」
「そういうことって生物部の部員ならみんなわかるもの?」と聞くと、
「部長・副部長をやるくらいの人は確実にわかる。けど、他の人でもわかるやつはきっと多いよ。」また、部長・副部長経験者である。
「ところで、生物室にエーテルはある?」と訊くと、
「うん、あるよ。」とのお答え。やはり、生物室の「鍵」である。
「生物室に入れる人なら手に入ると思うよ。」
「せめて靴の先の色がわかれば。」そう靴の先の色は赤・黄・緑と色分けされており、それで1,2,3年生の区別がつくのだ。もっとも、それと関係ないサンダルを履いている人のほうが実際は多いのであるが。それに、靴を履いていたから学内の生徒とは限らないが。
「学年がわかるね。」
次に、ぼくらは覚えたばかりの数学の知識をひけらかす(まだ高校生だから)話をしていた。
犯人(変質者)の条件
- 男
- 生徒用の上履きを履いてた。
- 麻酔薬に関する知識がある。
- 麻酔薬を手に入れられる。
- 生物室に入れる。
- 一人
ここで、私は
「ぼくは生物室の鍵を持っていないから、必要条件を満たしていないな。」
つまり、「生物室に入れる=鍵を使える=生物の部長・副部長経験者」であるから、「ぼくは必要条件のひとつを満たしていない」と主張したのだが、鴨志田は聞き入れなかった。。
「オマエに鍵なんか必要ないだろう。」
そう、物理部の部長(私のこと)になるには「錠前破りが得意」でなければならなかったのである。すなわち、物理部の部長経験者であると「生物室に入れる。」ということの「十分条件」をもれなく手にしてしまうのである。イヤーなおまけである。もっとも、私は生物・化学は苦手であるので、必要条件を満たしていない。
一方犯人の「十分条件」を考えてみるとこんなものがある。
- 生物部の部長・副部長
 |
「ところで、こんなミステリがあったらどう思う? 探偵がめちゃくちゃ論理的なヤツでさ。」さてさて、普通ならばここに「読者への挑戦状」が入るところだろう。だから、この話にも入れてみる。ただ、少し定型とは違う。
「コンパクト群の表現論なんかで語られてさ。」
「犯人を指摘する所なんか、数式だらけな話。」
「作家はMathematicaをワープロ代わりにしててさ。」
「......なんか、一般受けしそうにないな...おれにすら面白くないぞ...」
| ここまでに、犯人を示す証拠が全ての証拠がそろっているとは思わないし、そもそも、犯人が登場しているかどうかすら私にはわからない。いや、実際のところ登場していないと100%確信している。しかし、名探偵のあなたなら、きっと犯人を指摘してくれるに違いない。私と鴨志田の懸念を吹き飛ばしてくれるに違いない、と思うのだ。 犯人は一体誰なのだ... |
2000-07-23[n年前へ]
■WEBページの文体を調べてみよう 
「ノリノリ文体」の秘密!?
今日もまたいつものように
- お笑いパソコン日誌 ( http://www2s.biglobe.ne.jp/~chic/pilot.html )
すると、
- 文体模写してください( http://mentai.2ch.net/test/read.cgi?bbs=book&key=963421916 )
以前から、私も文体について調べてみたい、と思っていた。それも普通の文体ではなくて、WEBページの文体である。色々な面白いWEBページを読むたびに、「この面白さ・ノリの良さの秘密はどこにあるのだ?」と思っていたのである。そして、できることならば「そのノリノリ文体の秘密をこの目で見てみたい!」と切望さえしていたのである。もちろん、本当のところは「ノリノリ文体の秘密」が明らかになったならば、「そのノリノリ文体をパクッてやろう」という気持ちが私の中にあるのだ。文体だけ真似しても、「面白いページ」にはならないと言う気もするが、そんなことは考えてみてもしょうがないのだ。まずは、形から入ろうというわけだ。
そこで、今回は「ノリノリ文体」を書いているWEBサイトの文章をいくつかピックアップして、その「ノリノリ文体の秘密」を調べてみることにした。今回、ピックアップした文章はまず次の三つである。
- そりを言ってはお終いなのよ fromちゃろん日記(仮) ななゑ さん
- ( http://www.alpha.dti2.ne.jp/~nanae/nikki1999_8m.htm )
- 娘よ from 我が妻との闘争呉エイジ さん
- ( http://www.117.ne.jp/~kure/waga/yome12.html )
- 半角カナを使え! fromとろん 南野 輝 さん
- ( http://www2.justnet.ne.jp/~chic/TRON005.HTML )
そして、次に「男心と女心のギャップ」を全く違う視点から描く、まさに涙ナミダの物語「我が妻との闘争」から涙無しには読めない「娘よ」にも注目したい。
涙でなくて「笑い」と言えば、当然「お笑いパソコン日誌」から辿り、「半角カナを使え!」にも注目してみたい。本当はこの作者が文章を書いている印刷物も手元にあるので、その印刷物とWEBの文章とを比較してみたかったりもしたのだが、今回はパスさせて頂いた。
そして、WEBページの文章ではないが、当然この人
- 私の個人主義 夏目漱石
さて、今回は「文体の特徴の解析」の手段として、「文章構造可視化シリーズ」で作成した"wordfreq"を少し改造して使ってみることにした。以前、のバージョンから少し変えて、ファイルに落とす結果はスムージングをかけないそのままの結果にしてみただけである。とりあえず、そんな"wordfreq"を使い、WEBページの「一段落中の句点(。)と読点( 、)の数」を調べてみたのである。
何故、「一段落中の句点( 。)と読点( 、)の数」に注目したかというと、私はどうも読点の使い方が判らないのだ。文章の各部分が他のどの部分にかかるのかをちゃんと示したいのだが、どうも私の文章は変なのだ。もういっそのこと、文章の各部分がどこにかかるかわかるように各個とか矢印とか使いたくなるくらい、読点の使い方がわからないのである。その結果、読点をどうも多く打ってしまうような気がしているのである。
そこで、その勉強も兼ねて「一段落中の句点( 。)と読点( 、)の数」に注目しながら、WEBページの「ノリノリ文体」を調べてみたいと思うわけだ。
| ノミネートされた文章 | 一段落中の句点( 。)の数 | 一段落中の読点( 、)の数 |
| 私の個人主義 | 7.6 | 11 |
| コンクリートの隙間に | 4.4 | 7.6 |
| 新宿駅は電気羊の夢を見るか | 3.9 | 2.8 |
| 半角カナを使え! | 1.8 | 2.1 |
| 娘よ | 1.4 | 0.5 |
| そりを言ってはお終いなのよ | 0.4 | 0.9 |
この結果を見てみると、「ちゃろん文体」などは圧倒的に一段落中の句点(。)の数が少ない。また、同じように一段落中の読点( 、)の数も少ない。そして、「我妻文体」も同じように、一段落中の句点(。)の数が少ない。こちらの「我妻文体」は、一段落中の読点( 、)の数の少なさでは今回No.1である。
それに対して、偉大なる漱石の「私の個人主義」では「一段落中の句点(。)と読点( 、)の数」も実に多い。そして、私の書いた文章においても、その数はやはり多い。上の表は「一段落中の句点(。)の数」が多い順に並べてみたが、私の文章は二つとも、漱石の次に「一段落中の句点(。)と読点( 、)の数」が多い。
上の表では
私の個人主義 >> コンクリートの隙間に, 新宿駅は電気羊の夢を見るか >>半角カナを使え!, 娘よ >> そりを言ってはお終いなのよ
となっているが、これはWEBの「ノリノリ文体」とかなり良い一致をするのではないだろうか?つまり、
- WEBの「ノリノリ文体」は一段落中の句点( 。)と読点( 、)の数が少ない程良い
その推定を用いて「娘よ」の文章中における一段落中の読点( 、)の数の変化を眺めてみると面白いことが判る。文章中で、段々と「一段落中の読点(、)の数」が少なくなってきているのである。これは、きっと作者 呉氏が文章を書いている内に、気分が「ノリノリ」になってきて、その心の変化が「ノリノリ文体」としての特徴- 一段落中の読点( 、)の数が少ない - を示し始めたのではないだろうか?
 |
さて、今回はWEBページの「ノリノリ文体の秘密」を簡単に調べてみた。これからも引き続き、その秘密のさらなる姿を見てみたいと思う。そして、いつかその「ノリノリ文体」を私は身につけ、ノリノリWEBページなどを書いてみたりするのである。
とはいえ、それぞれの「文体」には作者の性格も強く現れているわけで、私の性格を直さないことにはそんな「ノリノリ」文体を身につけられないような気もするし、文体だけ真似しても「面白いページ」にはならないとか、形から入ってどうするとかいう声が聞こえそうであるが、それを言ってはダメなのだ。
2000-08-16[n年前へ]
■エアコンの風は心地よく吹くか? 
真夏の夜の夢 流体力学入門編
私は長野県の野辺山という高原で幼い時期を過ごしたせいか、暑さにとても弱い体である。なので、真夏の夜はエアコンが欠かせない体と根性になってしまった。エアコン無しではろくな夢が見られ無いどころか、眠れなかったりするのである。気持ちの良い「真夏の夜の夢」を見るためには、エアコンがとっても重要なのである。
つい先日、そんなエアコンの話題が「今日の必ずトクする一言」に載っていた。それが、
- エアコン用流体素子(PATPEND.)のナゾ
- ( http://www.bekkoame.ne.jp/~jh6bha/higawari.html#000819 )
- 復活する冷蔵庫脱臭剤のナゾ(1/f揺らぎと活性炭編)
- ( http://www.bekkoame.ne.jp/~jh6bha/higawari.html#000901)
(おそらくhiraxさんあたりがやってくれるのではなかろうか)と話題のパスまでされている。いきなり、ボーとしているところを授業で当てられた気分である。
とはいえ、「エアコンの流体力学」というのもちょっと興味のある話題でもあるし、パスされたからにはやってみなければなるまい。そういうわけで、真夏の眠れない夜のパズル代わりに挑戦してみることにした。
さて、部屋の中の「エアコンから送られる風の様子」を計算するということは、流体力学の計算をするということになる。流体力学の運動方程式(ナビエ・ストークス式)に代表されるような方程式群を解かなければならないのである。そこで、以前
の時にいじりかけたMichael Griebel氏らによる非圧縮性流体のNast2Dのコードをもう一度引っ張り出して使ってみることにした。このNast2Dは非圧縮性二次元流れを計算する教育用のソースコードである。詳しくは- TUM INFO V- Homepage - ( http://www5.informatik.tu-muenchen.de/home_us.html )
- Numerical Simulation in Fluid Dynamics A Practical IntroductionISBN 0-89871-398-6
計算するモデルは次の図に示すような部屋である。四畳半一間であるかもしれないし、100畳以上の大きな広間かもしれないが、とにかく正方形の部屋だ。向かって左の青い丸部分にはエアコンがあり、そこから冷たい空気が送られてくるのである。そして、この部屋には何故かタンスがおいてある。「やっぱり、この部屋は四畳半一間じゃないの」というツッコミは言ってはいけない約束である。とりあえず、このタンスが向かって下側にある紫の部分である。このタンスが、エアコンから送られてくる冷た〜い空気流の障害物となるのである。
 |
暑い真夏の夜に、こんな部屋をエアコンで涼しくする時のことを考えてみよう。気持ちよく眠るために、何はともあれエアコンのスイッチを入れるわけだ。そうしないと、暑くて眠れないから当然である。
そして、そのエアコンには送風モードが何故か三つあるのだ。次のような三種類の送風、
- 真っ直ぐ送風するモード
- 単純な首振り送風をするモード
- 山本式エアコン用流体素子を用いた送風をするモード
空気流の速度分布の計算結果を次に示してみよう。
|
| を用いた送風の場合  |
また、これらの場合の計算結果を動画で示したものをMPEG4形式のAVIファイルとReal形式のファイルにしたものを以下に置いておく。エアコンから空気が送られる様子を知るには、何はともあれこの動画を見て頂きたい。なお、手元のRealProducerの制限のために、このReal形式のファイルは古いバージョンのRealPlayerだとアップデートが必要になってしまった。また、MPEG4のCodecが導入されていない場合には、DivXなどをインストールする必要がある。
とりあえず
- 真っ直ぐ送風している場合 MPEG4 AVI ( 289KB ) Real形式( 73KB )
- 単純な首振り送風の場合 MPEG4 AVI ( 577KB ) Real形式( 89KB )
- 山本式エアコン用流体素子を用いた送風の場合 MPEG4 AVI( 693KB ) Real形式 ( 92KB )
また、それぞれのMPEG4形式の動画のファイルサイズを見れば、それぞれの場合の送風による空気流の速度分布の複雑さは一目瞭然である、と思う。真っ直ぐ送風している場合はとにかく単純な速度分布であって動画ファイルサイズも結果的に小さくなっているのに対して、山本式エアコン用流体素子を用いた送風の場合はかなり複雑な速度分布になっていて動画ファイルも結果的に大きくなっているのである。
動画を見ることができない人のために、それぞれの場合の連続した3つの瞬間における部屋内の空気流の速度分布の静止画も示しておく。
1 | 1 | を用いた送風の場合 1  |
 |  |  |
 |  |  |
これを見ると、「真っ直ぐ送風している場合」にはエアコンの正面は強烈に風が当たっている(つまり冷えまくっている)ことがわかるが、タンスの陰になっている部屋の隅などはほとんど空気が動いていないことがわかる。また、「単純な首振り送風の場合」は送風方向を動かしているとはいえ、その送風方向の変化はかなりゆっくりであって部屋の中の空気流の速度分布はそれほど急激には変化していないことも判ると思う(そういう風に計算しただけではあるが...)。いずれにせよ、もしもこの部屋の中にあなたがいたとしたら、体の決まった部分にのみ冷た〜い風があたることになるわけだ。それは体にはちょっとよろしくなさそうである。
一方、「山本式エアコン用流体素子を用いた送風の場合」は時々刻々と送風方向が変化しており、まるで部屋を舐め回すかのように、冷た〜い空気が送られていることがわかると思う。この部屋の中にもしあなたがいたとしても、体のごく一部分だけに冷たい風が当たるようなことはなく、それほど体に悪くないことが予想されるわけである。
さて、このページもかなり重いページになってきた。本来はこのタンスの裏側の空気が澱みやすい場所の「空気の入れ替わり」を、送風の具合を変えた上で調べてみたいわけであるが、それは次回のお楽しみ、ということにしておきたい。とりあえず、「真夏の夜の夢 流体力学入門編」はここら辺で終わりにしたい。
さて、夏休というわけでこんな景色のところで気持ちの良い風に吹かれてみたりするわけである。この写真の先の方の海の向こうに見えているのは左が伊豆半島で、右が三保の松原の辺である。

暑い夏の夜はエアコンが欠かせない体ではあるけれど、気持ちの上で言えばエアコンよりはおんぼろの扇風機の方が好きだし、扇風機よりも山の上の風の方がずっと好きだ。いつか、山の上を吹き抜ける風の音を録音して、その1/f揺らぎでも調べてみようかなと思うのである... それとも、そんなことをしてもツマラナイだけかな?

