2008-05-02[n年前へ]
■理科の教科書に出てくる「仕事」と「駅前で聴く音楽」 
力積で考える「カミソリパンチ」と「ググゥーッと押し込む打撃」の「力積」は「力の大きさと力が働く時間を掛けあわせたもの」です。その一方、「力と変位を掛け合わせた（内積）もの」を、理科の教科書の中では「仕事」と呼びます。
中学か高校の頃、理科か物理の教科書の中で「仕事」という言葉が出てきたときに、何だかその言葉の感覚と教科書の中での定義がズレていて首を捻ったような覚えがあります。たとえば、Wikipedia に「仕事とは呼ばない例」として挙げられているようなこと
人が重い荷物を抱え・支えている状況では、荷物は静止していて、エネルギーは変わらない。つまり、この場合、人は荷物に対して仕事をしていない。を聞きながら、それは仕事でないのかぁ……!?と悩んだわけです。「重い荷物を抱え・支えている状況」はとてもしんどそうなのになぁ……と感じました。それは「仕事」ではないかもしれないけれど、筋肉がパンパンにつく肉体改造・大成長状態だろうに……と思ったのです。
私と同じように、理科の教科書を読みながら、頭の中に大きなハテナマークを浮かべた人はきっと多いと思います。
先日、「手作り三次元グラフ」と"Life Work"や「"複雑極まりない"複素平面」上に「仕事」と「趣味」を描くといったラクガキをしました。そのとき、”理科の教科書の中の「仕事」の説明を読みながら、頭に浮かんだハテナマーク”を思い出しました。
あのラクガキ中の「他人の満足」という軸は、「その人がどれだけ他の人を満足させたか・その人の力で他の人（の心を）どれだけ動かしたか」という、まるで理科の教科書に出てくる「仕事」なのかもしれない、と感じたのでした。
駅前で誰かが演奏している音楽を聴いて心が動かされたとき、「何だか心の中に豊かなエネルギーが入ってきたなぁ」と思ったりもします。それを、理科の教科書を思い出しながら言うならば、「あぁ誰かに仕事をされたんだなぁ」と感じたりするのです。
「力積」と「仕事」はイコールではありません。もしも、「自らを脅かし・揺るがし、新たな出会いや発見がある」としたら、それは「仕事」よりは、力積に近いものなのだろうか、と思っています。
2008-06-03[n年前へ]
■「GPUを使った物理計算プログラム」と「スクリプト言語」
日経エレクトロニクスを読んでいると、「GPUを使った並列計算で物理シミュレーションを高速化」という記事があった。PC用のグラフィックボードに搭載されている描画処理LSI(GPU)での物理計算の解説記事で、流体などの挙動を粒子群として計算するプロメテック・ソフトウェアの計算ソフトウェアを題材に、GPUで物理計算をする効果や注意点などを解説したものだった。そういえば、つい最近、「NVIDAがGPUベースのレンダリングソフトNVIDIA Gelato Proを無償提供開始」というニュースもあった。
ところで、GPUを使ったシェーダプログラム言語であるGLSL (OpenGL Shading Language)に触れたときに感じた新鮮さは、「GLSLで書かれたプログラムは、実行時にコンパイルされる」ということだった。シェーダのソースコードを書き換えると、そのシェーダを使ったアプリケーション実行すると、その実行時にシェーダプログラムがコンパイルされ動くのである。
その感覚はとても新鮮で、「Ｃ言語のようでＣでない変なスクリプト言語」をいじっているような面白い感覚を味わった。また、自然に並列計算される具合が、何だか非同期で動くアプリケーションをスクリプト言語で書く感じに似ているのだろうか、と感じたりもした。
JavascriptやRubyや…といったスクリプト言語を使うプログラマが、GPUを使ったプログラムをいじってみると、これが結構ハマったり楽しむことができたりするものかもしれない。
2008-06-06[n年前へ]
■体感・実感バストシミュレータの内側（粒子群）を見る
「GPUを使った物理計算プログラム」と「スクリプト言語」で読んだ日経エレクトロニクスの、「粒子が動いて流体を表現するさまを示した図」が見ていて綺麗だったので、先日作ったプログラム、粒子法を使った（加速度センサ対応）体感・実感バストシミュレータにも表面レンダリングだけでなく粒子レンダリングの機能を付けてみました（バイナリはここに置いておきます）。
アプリケーションを実行させて、「皮膚」＝表面層の内側を眺めたさまは下の動画のようになります。
2008-06-28[n年前へ]
■「Mathematica開発者のウルフラム」と「ファインマン」
今週頭に「数式処理アプリケーションのMathematicaが最初にリリースされてから、今日で20年たちました」と、開発者Stephen WolframからMathematicaユーザにメールが送られてきた。スティーブン・ウルフラムが28才の時の1988年の6月23日にMathematica 1.0 が出荷されたのである。
For twenty years we've pursued our long-term vision for Mathematica.
Mathematicaは結局のところ、パターンマッチングを延々と行うプログラムである。データベースに登録されているパターン・規則にもどづいて、与えられた数式を置換していくことにより、Mathematicaは解（や所望の結果）を得る。
ところで、「ファインマン物理学」で有名なR.P.ファインマンはカリフォルニア工科大学で1983年から1985年までの間、計算機科学の講義（ファインマン計算機科学）をしている。その頃の学生がスティーブン・ウルフラムである。
ファインマンは「科学とは何か」の中で、「数学とはパターンにすぎない」「数学とはパターンを探すことだ」と端的に短く書き表している。この言葉を思い起こしながら、（おそらくそんな言葉を聞いていただろう）彼の学生でもあったウルフラムが「パターンマッチングによる数式処理アプリケーション」を商品化し市場に広まらせたのだ、と考えてみると何だか「面白い繋がり」を感じる。そんな繋がりを思い浮かべながら、Mathematicaの20年を集めたスクラップブック を眺めてみると、きっと楽しいと思う。
I'm looking forward to the next 20 years and hope that you'll continue to follow Mathematica on this exciting journey.
-- Stephen Wolfram
2008-07-18[n年前へ]
■エクセルでシミュレーション Vol.1 [静電界準備 編]
「表計算プログラムでシミュレーションをする」というのは、物理などにそれほど詳しくない人が、複雑な数式で記述された世界を感覚的を大雑把に・感覚的に理解するのに、とても向いています。もちろん、そこには、かなり単純であることなどの前提条件がいくつもあります。けれど、自分のコンピュータで、マウスを動かしキーボードを少し叩くだけで、物理シミュレーションができたりすると何だか少し嬉しくなりますし、その計算過程を通して、「自然なこの世界」を「自然に」納得できる、というのは（私たちのような勉強世界からの REST OF US にとっては）とても素晴らしいと思います。
ところで、現在では”表計算プログラム＝マイクロソフトのエクセル(Microsoft Excel)”だと考える人も多いことでしょう。だから、上に書いたことを言い換えれば、「エクセルでシミュレーションをする」のは、とても楽しい勉強になるということになります。
自分自身でエクセルでシミュレーションをすることもたまにあります。また、「エクセルで物理現象のシミュレーションをする」という趣旨の講習会にも、何回も関わってきました。ふと、そういった場で得たことを一回整理してみようと思いました。そこで、一番初めの今日は、「静電界を記述するポワソン方程式をエクセルで計算するための前準備（事前確認）」をしてみました。
まず、静電場を記述するポワソン方程式をテーラ級数展開することで離散化し、差分方程式に変えてみます。２次元世界を離散化するということは、エクセルの表がそうであるように「世界（画面）をセルで分割する」ということです。
上で（x,y座標空間での）差分方程式にしたものを、さらにエクセル（表計算ソフトウェア）で解くときのやり方を図解したものが下の図です。「ある点の電位（φ）は上下左右の電位の平均にその点の(係数がかかった)空間電荷を加えたもの」になっているわけです。
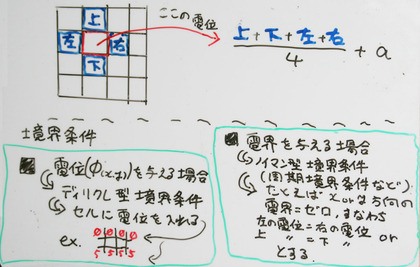
また、2種類の境界条件（電位を指定するディリクレ条件/電界を指定するノイマン条件）をどのようにエクセル上で処理するか、というのが下の部分になります。
こういったセルの値が「（そのセル自身を含む）セル間の関係式」で表わされるような計算式を解くためには、エクセルの設定で「反復計算を行う」という設定を有効にしておく必要があります。エクセルのバージョンによってその設定メニュー場所は違いますが、たとえば、下の画面はExcel 2003の設定ダイアログの例です。
以上で、「静電界を記述するポワソン方程式をエクセルで計算するための前準備（事前確認）」が終わりましたから、次は実際に「身近な静電界」をエクセルでシミュレーション計算してみたいと思います。
」など。