hirax.net::Keywords::「物理」のブログ

■MiosoftはApple株でいくら儲けているか?　

価値観は線形なままで

　ユング心理学では因果関係が無い偶然の一致を「シンクロニシティ(共時性)」と呼ぶ。いろいろ意見の違いもあるだろうが、私は「シンクロニシティ(共時性)」は結局偶然のせいではなく、世の中の流れの要請による必然なのではないかと思うのである。
　と、いきなり訳のわからない話だが、今回の話は「今日の必ずトクする一言」の

• 対数軸証券グラフのナゾ

と似て非なる話である。まず話は、「今日の必ずトクする一言」のwebmaster氏からメールを頂いたところから始まる。「株価表示グラフで値の軸を対数軸にできないか」、というものである。そこらへんのこと、及び、詳しい考察は「対数軸証券グラフのナゾ」を読んでもらいたい。というわけで、今回の話は残念ながら「シンクロニシティ」ではないのであった。

　ともあれ、webmaster氏のメールのおかげで、株価の値軸が妙に頭に残る最中に、私は「MicrosoftはApple株でいくら儲けているか?」という疑問が沸いて、Appleの株価を見に行ったのである。何しろ、MicrosoftはAppleの大株主である。

最近１年間のAppleComputerの株価変動(左)とアップルコンピュータの株価変動(右)

　一見似ているように思える。しかし、よく見てみると軸が違っている。左のAppleComputerの株価変動は対数軸で表されている。「株価表示グラフで値の軸を対数軸にできないか」という言葉が頭にあったせいで気づいたわけだ。そこで、この違いが新鮮で「今日の必ずトクする一言」のwebmaster氏への返信に至ったわけである。

　それでは、左のAppleComputerの株価変動をリニアな軸に変換してみよう。

対数軸のAppleComputerの株価変動(左)とリニア軸のAppleComputerの株価変動(右)

　印象が全く違う。右の線形軸のグラフは値軸の間隔が等間隔になっているのがわかると思う。それに対して対数軸で表されている右側は上に行くほど間隔が短い。右の線形軸では株価が急激に上昇しているのが実感できる(私は)。株取引的な考察は「対数軸証券グラフのナゾ」の方にあるので、ここでは本題の「MicrosoftはApple株でいくら儲けているか?」に戻る。

　さて、このグラフのようにApple株は急上昇中なわけで、問題の「MicrosoftはApple株でいくら儲けているか?」であるが、97/08/08当時の13ドル前後の株価で一億五千万ドル分のApple株を買っていたとしたら、現在は80ドルくらいであるから、およそ6倍。すなわち、一億五千万ドルから九億ドルになっていることになる。うーん、たまらん。800億円近い差が有る(線形的な発想)。

　さて、最初の疑問はこれで解決したのだが、わが「できるかな?」でも株価の軸の

• 対数軸
• 線形軸

の違いについて考えてみたい。いや、株価というよりは価値観と言い換えたほうが良いかもしれない。私は経済オンチである。株価の売買はしたことがない。すると、金銭に関する軸は線形軸が自然なのである。「hogehogeが何倍になった」というのが自然にわかるからである。しかも、単位は100円位なのだ。
　日頃、実験を行っている時などは

「たかだか一桁の変化だろう。」

などと対数軸の感覚に支配されているのであるが、こと経済になると線形軸の感覚に支配されるのである。これは私が貧乏であるからかもしれない。1万円はどんなときも1万円なのである。10万円と11万円の違いも、100万円と101万円の違いも同じなのだ。これが一億円と一億一万円でも同じである。何しろ、そんなお金と無縁なのである。であるから、貧乏な金銭感覚をそのまま線形で延長してしまうのである。「金銭に関する差の感覚」といってもよい。

　これは人によっても違うだろう。私と違うブルジョアジーな人であれば、例えば、車を買うときに

「300万円の車を買うから、30万円のカーナビを一緒に買っても誤差みたいなものだ。」

という人もいると思う。また、「一億円と一億一万円は同じだ」と言うだろう。これなどは経済に関する対数軸の感覚の一種だと思う。この人は「金銭に関する比の感覚」を持つ人である

　さて、こういうことを考えていくと、金持ちの1万円と私の1万円は価値が違うことにいまさらながら気づくのである。私は1万円もらったら大喜びだ。しかし、同じだけビル・ゲイツを喜ばせようと思ったら、九億ドル位は必要だろう。そういうことを考えると、経済社会は実に対数軸である。いや、むしろ世の中が対数軸だと言ったほうが良いだろうか?

　今回の話とやはり似て非なる話がロゲリギストの「第四物理の散歩道」の「理解の形式」に述べられているので、興味の有る方は読むと面白いと思う。

　さてさて、同じ題材をとってみても経済オンチの私が作る「できるかな?」は「「対数軸株価グラフのナゾ」」とは違い、ずいぶんと変な話になってしまったようである。しかし、それが個性というもの。みんなが同じではつまらない。

ともあれ、価値観に対する評価軸は線形軸の方が良い、と思う私であった。

■沸点と数学の挑戦状　

みつからない「解決編」

いったい、いつから疑問に思うことをやめてしまったのでしょうか?　いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか? 　いつだって、どこでだって、謎はすぐ近くにあったのです。 　何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。 加納朋子　ななつのこ　より

　加納朋子の「ななつのこ」という小説を読んだ。創元推理文庫から出ているのだから、ミステリといっても良いだろう。私の好きな北村薫の「空飛ぶ馬」に始まる「円紫さんと私」シリーズによく似た雰囲気を持つ本である。

　それを読んで、ふと思い出した。

　私が通っていたM高校の話だ。M高校は武蔵野の玉川上水のほとりにある。

　そのことを聞いたのは月曜の朝だ。日曜日の昼間に変質者が現れたというのである。目撃した人によれば、変質者は生徒用の上履きを履いていて、手には白い布を持っていたという。顔などはよくわからなかったそうだ。目撃者に驚いた変質者は逃げてしまい、白い布を落としていった、というのだ。
　
　それだけなら、「単なる変な奴がいた」ということで話は終わった筈だ。問題は、その白い布に麻酔薬が含ませてあったという点だった。悪ふざけではすまない。

　私は友人の鴨志田とその事件について話をしていた。気になることがあったからだ。変質者が目撃された場所が問題だったのだ。図に描くとこんな感じだ。

M高校2F平面図

現場写真

　そこは2階の中では職員室から一番遠い。一番校門に近い玄関を揚がった所である。そして、生物室の隣だった。
　生物室は、普通の教室とは違う。通常は鍵がかかっているし、それは鍵がかけられるということでもある。

　生物部の部長・副部長は生物室の鍵を使える立場にあった。そして、鴨志田は生物部の部長だった。

「変質者は生物室に出入りできる奴かな?」
「生物の部長・副部長経験者ってこと?」
「うーん。」

これはどうにも重大な問題だったのである。

「麻酔薬ってクロロホルムとか、かな?」と鴨志田にぼくが言うと、「立て板に水」状態で、彼の推論を聞かせてくれた。

「いや、きっとエーテルだね。」
「今時、クロロホルムなんて使われていないんだよ。」
「副作用もあるしさ。」
「あと、沸点を考えてみろよ。」
「エーテル、つまりジエチルエーテルDiethyl Ether ( (C2H5)2O )は沸点が34.6℃だ。」
「それに対して、クロロホルムChloroform ( CHCl3 )は沸点が61.7℃だ。」
「ハンカチにクロロホルムを含ませて顔に当ててもなにもおきない。」
「だけど、エーテルは人間の顔にあてたら、体温のせいで瞬間的に気化するんだよ。」
「つまり、エーテルの気体で顔の周りが覆われるわけだ。」
「呼吸なんかしたらエーテルを吸わざるをえないだろ。」
「だから、クロロホルムとかよりエーテルのほうが、変な用途には向いているんじゃないかな。」
「もっとも、即座に気を失うとは思えないけどね。」

　なるほど説得力はある。いや、ありすぎるといっても良い程だ。コイツ、むちゃくちゃ怪しいヤツである。犯人候補No.1である。一朝一夕で考えた理屈とは思えない。
「そういうことって生物部の部員ならみんなわかるもの?」と聞くと、

「部長・副部長をやるくらいの人は確実にわかる。けど、他の人でもわかるやつはきっと多いよ。」

また、部長・副部長経験者である。

「ところで、生物室にエーテルはある?」と訊くと、

「うん、あるよ。」
「生物室に入れる人なら手に入ると思うよ。」

とのお答え。やはり、生物室の「鍵」である。

「せめて靴の先の色がわかれば。」
「学年がわかるね。」

そう靴の先の色は赤・黄・緑と色分けされており、それで1,2,3年生の区別がつくのだ。もっとも、それと関係ないサンダルを履いている人のほうが実際は多いのであるが。それに、靴を履いていたから学内の生徒とは限らないが。

　次に、ぼくらは覚えたばかりの数学の知識をひけらかす(まだ高校生だから)話をしていた。

犯人(変質者)の条件

• 男
• 生徒用の上履きを履いてた。
• 麻酔薬に関する知識がある。
• 麻酔薬を手に入れられる。
• 生物室に入れる。
• 一人

これは犯人の「必要条件」といえる。

ここで、私は
「ぼくは生物室の鍵を持っていないから、必要条件を満たしていないな。」
つまり、「生物室に入れる=鍵を使える=生物の部長・副部長経験者」であるから、「ぼくは必要条件のひとつを満たしていない」と主張したのだが、鴨志田は聞き入れなかった。。
「オマエに鍵なんか必要ないだろう。」
そう、物理部の部長(私のこと)になるには「錠前破りが得意」でなければならなかったのである。すなわち、物理部の部長経験者であると「生物室に入れる。」ということの「十分条件」をもれなく手にしてしまうのである。イヤーなおまけである。もっとも、私は生物・化学は苦手であるので、必要条件を満たしていない。

一方犯人の「十分条件」を考えてみるとこんなものがある。

• 生物部の部長・副部長

これだけで、全ての必要条件を満たしてしまうのである。といっても、それはやはり単なる「十分条件」である。しかし、上の必要条件は明らかに「生物部の部長・副部長」よりも大きいだろうから、「必要十分条件」にはなりえないだろう。

犯人と生物部の部長・副部長と私に関する関係

「ところで、こんなミステリがあったらどう思う?　探偵がめちゃくちゃ論理的なヤツでさ。」
「コンパクト群の表現論なんかで語られてさ。」
「犯人を指摘する所なんか、数式だらけな話。」
「作家はMathematicaをワープロ代わりにしててさ。」
「......なんか、一般受けしそうにないな...おれにすら面白くないぞ...」

　さてさて、普通ならばここに「読者への挑戦状」が入るところだろう。だから、この話にも入れてみる。ただ、少し定型とは違う。

読者への挑戦状

ここまでに、犯人を示す証拠が全ての証拠がそろっているとは思わないし、そもそも、犯人が登場しているかどうかすら私にはわからない。いや、実際のところ登場していないと100%確信している。しかし、名探偵のあなたなら、きっと犯人を指摘してくれるに違いない。私と鴨志田の懸念を吹き飛ばしてくれるに違いない、と思うのだ。 　犯人は一体誰なのだ...

■ビックエッグの力学　

ドームを支える空気圧の謎

　この回は(トンデモ話)であり、中途半端であるのだが、反省を込めてこのままにしておく。直すのが、面倒くさいわけではないので、念の為。

　日本シリーズ'99をやっている(いた)。私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。そういえば、今年はドーム決戦である(だった)。ドームといえば元祖「東京ドーム」だろう。「東京ドーム」のWEB

• 株式会社東京ドーム　(http://www.tokyo-dome.co.jp/about/index.htm )

を、眺めていると、こういう記述がある。

東京ドームは、空気膜構造によるエアドーム。つまり内部気圧を外気より0.3％高くして、400トンもの超特大楕円形の屋根を膨らませるのがドーム建築のポイントなんだ。 　ところで、この気圧差0.3％は、ビルの1Fと9Fぐらいの違いがある。とはいえ中と外の違いを体感することはほとんどない。

　たった、0.3%の空気圧の差で400トンを支えるとは、ものスゴイ。すぐには納得できない数字である。別に疑い深い私でなくても不思議に思うことだろう。

　そこで、確かめてみることにした。まずは、東京ドームの面積をx(m) * x(m)としてみる。すると、持ち上げることのできる重さ(トン)は、

• 0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x / 1000(kgからトンへ)* 9.8(Nから重力へ)

と計算できる(この式には実は間違いがある。詳細は後で...)。その結果を示してみる。

東京ドームのサイズに対する「持ち上げることのできる力」の計算結果
横軸=サイズ(m), 縦軸=「持ち上げることのできる力」(トン)

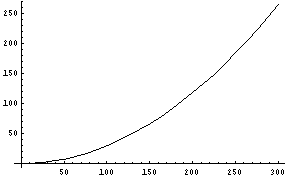　先の、Webから東京ドームのサイズを見てみると、x = 180mである。すると、持ち上げられる天井の重さは100トン程度であるということになる。おやおや、先の「400トンの天井を持ち上げる」というのとはずいぶん違う。これでは、天井を支えきれない。

東京ドームのサイズ

　そこで、高さによる大気圧の差を導入し、天井近くの高い場所では「外部の気圧が低い」という条件を導入してみる。0.3%というのは地上での比で、天井のある上空ではさらに差があるとしてみるのだ。うーん、強引である。

　さて、ここから後は(実は前も)トンデモ話になっているので眉に唾をつけて読んで欲しい。それを指摘して下さった、読者からの手紙への返事(とほぼ同じ内容)を下に示しておく。

青木さんへの手紙> 高さによる圧力の差は、高さの異なる二点間に存在する空気> の重さに見合ったものです。したがって、ドームの内部でも> 高いところほど圧力は低くなっている筈です。　その通りだと思います。WEB中で「うーん、強引である。」と書いたのはまさにその理由です。　それにも関わらず、強引な論法を続けたのは、文章の最後に「謎は解けないのに、東京ドームは存在している。 少し、くやしい。 」と書いた理由と同じです。まるで、「宇宙人が水道橋の駅前駐車場にUFOを停めて、サラ金に入って行くのを目の当たりにしている」ような、気持ちなのです。くやしいと強引になるのです。あぁ、何て人間らしいのでしょうか...　また、計算をしていた時に少し勘違いをしていました>もし、ドームの内外の温度が等しければ、地上でも天井でも内外の差圧は>同じになるはずです。と仰るとおり、差圧は等しいわけですが、それを0mにおける大気圧に対するパーセンテージに直すと、高度が高くなればなるほど、そこの気圧に対してはパーセンテージは高くなります。計算をしていた時にその「パーセンテージが高くなる」ことを「差圧が高くなる」ことと同じに扱うという間違いを犯してしまいました。もちろん、基準の気圧が小さくなっているので、パーセンテージが高くなっても本当は差圧は変わらないわけです。「考えることを手抜きしていた」と言ってもよいかもしれません。要反省です。>ドーム内の温度が高ければ空気の密度> が減少し、天井の位置での差圧はより大きくなり、天井を支> えるのに有利に働きます。これは、浮力によって天井が持ち> 上げられていると考えても同じ事です。> という訳で、ドーム内外の温度差が逆転する夏と冬とでは天> 井を支えるのに必要な圧力を変えなければならないと思うの> ですが本当はどうなんでしょうか。　これは面白そうですね。そういえば、学生時代に地殻物理学を専攻していたのですが、夏と冬の大気圧の違いから、地殻歪の大きさに関係づけて、地震の予言をするなら、「冬に発生する」といった方が良い、話(もちろんかなり冗談で)をしていた先生がいました。その先生に「今回のトンデモ話」がばれたら、大目玉をくらうこと間違いなしです。　ビックエッグの謎は深まるばかりです。それでは、また。------------------------------------------------------------------ch3coohさんへの手紙> > >12/(100*100)*1000= 1.2g/cm2となります。> > >> > >地上での大気圧は約1Kg/cm2なので、上の値は> > >1.2%程度となり、　ここが疑問だったのですが、これは1.2%でなくて、0.12%ですね。なるほど、0.3%よりも小さいですね。実に納得です。　さて、他の方からの指摘もあり、私の計算には> ＞0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x > / 1000(kgからトンへ) * 9.8(Nから重力へ)> に１０１３（標準気圧 hPa）がかかっていないことが気になりました。　という間違いがあることがわかりました。全てはここが原因だったようです。　全ての疑問が解決しました。いやぁ、お恥ずかしい。また、他にも色々と面白い情報ありがとうございます。

　ひとつわかったことは、間違いをすると読者からの手紙が沢山来るといううれしくもつらい事実であった。ここから、あとは封印したい思いで一杯なのだが、自戒を込めてこのままにしておく。しつこいようだが、直すのが面倒なのではない。

　それでは、高さによる大気圧の差を計算してみる。理科年表から15℃の「標準大気の場合の高さと気圧の表」を見てみる。　ちなみに、東京ドームの温度は、「ガス熱源による冷暖房システムにより、夏期は28℃の冷房、冬期には18℃程度の暖房が行われている」とある。今回の計算は外気の温度が15℃で、内部は冬期には18℃程度の温度に調整されているものとしておこう。
　標準気圧は海抜0mで1013mbであり、200mでは989.5mbである。理科年表が古いのでPascal値でなく、mb表示になっている。

　これから、1m当たりのmb変化を計算すると、0.12mb/mとなる。比率に直すと、0.012%/mということになる。例えば、「ビルの1Fと9Fぐらい」の高さの差は30m位であろうから、それを大気圧の比に直すと、99.6%位となり、先の記述と大体合う。

以下に、高度に対する大気圧の差(の比 %)を示してみる。

高度に対する大気圧の比
横軸=高さ(m), 縦軸=大気圧の比(%)

　このグラフで30mの場所を見てみると、99.6%位というわけだ。これが、先のWEB上の「この気圧差0.3％は、ビルの1Fと9Fぐらいの違いがある。」という説明と合うわけである。

次に必要なのはドーム外部と内部の大気圧の比から、力に直してみる。基準面からの高さ0mにおける気圧を1hPaとして、1hPa = 10^2 N/m^2 = 10^2 m^-1 kg s^-2という単位換算を使うと、持ち上げることのできる重さは、

• (100-大気圧の差(の比 % )) / 100(%から単なる比へ) *9.8(重力に換算) / 1000(kgからトンへ)* 100(hPaからN/m^2へ) * x^2(ドームの面積)

という式で計算できる。

　東京ドームの高さは「グラウンド面から　61.69m」とあるので大雑把に100mとしてみる。

天井の高さを100mとした時の、東京ドームのサイズに対する「持ち上げることのできる力」
横軸=東京ドームのサイズ(m), 縦軸=「持ち上げることのできる力」(トン)

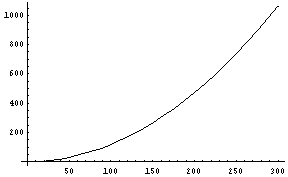　この計算結果によれば、東京ドームのサイズを180mとした時には、「持ち上げることのできる力」は400トン位になっている。ということは、先のWEBの記事と大体一致するわけである。

　しかし、この計算では致命的な欠陥がある。天井の高度が低いときには、400トンを持ち上げるためにはもっと高い「ドーム内部の圧力を必要とする」ことだ。

　例えば、0.3%空気圧の差の条件で、「天井の高度」に対する「持ち上げることのできる力」を計算してみると、次のようになる。

「東京ドームのサイズ」と「天井の高度」に対する「持ち上げることのできる力」
横軸=「天井の高度」(m), 縦軸=「持ち上げることのできる力」(トン)

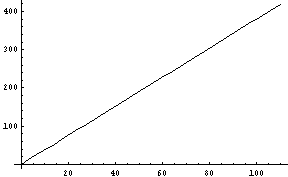　これでは、天井の高さが下がるとますます天井の重さを支えきれなくなってしまう。それに、そもそも天井をどうやって持ち上げたのだ?屋根を持ち上げるインフレートという作業はどうやって行ったのだろう?

　今回の計算は謎が増えただけかもしれない。謎は解けないのに、東京ドームは存在している。
　
　少し、くやしい。

■「星の王子さま」の秘密　

水が意味するもの

　今回は、Saint-Exuperyの「星の王子さま」- Le petit prince -について考えてみたい。しかし、メルヘンな話を期待する方は、おそらく失望することだろう。もし、今持っているイメージを壊したくない方は、今回の話は読まないほうが良いかもしれない。

　おそらく一般的に多いであろうイメージの「星の王子さま」というものは、私はそれほど好きではない。よくWEBで見かける「この本は、真実を見る目を失いかけた大人のための童話です。」というイメージである。私も、かつてはそういう認識だった。そして、「それだけでは、何かもの足りない」という感じがしていた。そのため、「星の王子さま」を好きではなかったのだ。

　しかし、

• 「星の王子さまの世界 - 読み方くらべへの招待 -」　塚崎幹夫著　中公新書

を読んで、そのイメージが一変した。これまで、「星の王子さま」の側面、あるいは仮面しか読んでいなかったことに気づかされた。読み方が足りないことに気付かされたのである。「星の王子さま」の底に流れているものに気付かなかったのである。実は「何かが足りない」わけではなく、私の読み方が浅かったのである。先の「この本は、真実を見る目を失いかけた大人のための童話です。」というイメージは私の読み方が浅かったせいであって、もう少し深く読めば、「真実から目を背けている人への告発・遺言」と受け取ることができたはずなのであった。

　さて、今回は私なりの「読み方」をしてみたい。具体的には、「水」というキーワードにこだわって解釈を行ってみるのだ。何故か、私はこの「星の王子さま」の中で「水」というキーワードに「深い何か」を感じるのである。

　何故、こういう単語にこだわる読み方をするかと言えば、それは塚崎幹夫氏の「星の王子さまの世界- 読み方くらべへの招待 -」の影響である。その内容の紹介を少し紹介しておく。

　塚崎幹夫氏は、 話の冒頭に出てくる「ゾウを飲み込むウワバミ」が何かもう少し深いものを指しているのではないか、と考える。「本当にもののわかる人かどうか」知るために、主人公が人に見せる「ゾウを飲み込むウワバミ」が何か深いものを指しているのではないか。「半年のあいだ、眠っているが、そのあいだに、のみこんだけものが、腹のなかでこなれ」そして次の獲物をのみこむウワバミは何を指しているのか、と考えた。
　そして、次のような年表を示す。

• (1937.7.7 日本、中国侵略開始)
• 1938.3.10 ドイツ、オーストリア侵略
• 1938.9.29 ドイツ、チェコ侵略
• 1939.3.15 ドイツ、チェコ解体
• (1939.4.7 イタリア、アルバニア占領)
• 1939.9.1 ドイツ、ポーランド侵入
• 1940.4.9 ドイツ、デンマーク、ノルウェー侵入
• 1940.5.10 フランス、ドイツに大敗
• 1940.11 Saint-Exuperyヴィシー政府に失望し、アメリカに亡命、その後、ヴィシー政府がSaint-Exuperyを議員に任命する。(どこかで聞いた話)

　ここから、半年毎に獲物を飲み込むウワバミはドイツのことを指している、と考えるのだ。
　つまり、ゾウを飲み込むウワバミが、帽子にしか見えないことが「真実を見る目を失いかけた」といっているのではない。これは、ウワバミの中で飲み込まれつつある動物のことを考えることができないことを、「真実を見る目を失いかけた」と言っているではないだろうか。もちろん、そのウワバミとは文字どおりのウワバミではなく、違うものを意識した話なのである。

同じように、「ぐずぐずしてはいられないと、一生けんめいになって」描いた「3本のバオバブ」は挿し絵についても考察を巡らせている。 「(バオバブは)星の上いちめんに、はびこります。」 「バオバブはほうり出しておくと、とんだ災難になるんだ」 「まだ、小さいからといって、バオバブの木を三本ほうりっぱなしにしておいたものだから...」 「ですから、ぼくは、一度だけ日ごろのえんりょをぬきにして、こういいましょう。<みんな、バオバブに気をつけるんだぞ！>」 「ぼくの友人たちが、ぼくと同じように、もう長いこと知らないで危ないめにあいかけているので、気をつけるんだよ！といいたいためです。」 　塚崎幹夫氏はこれら「3本のバオバブ」はドイツ・イタリア・日本を指しているのではないかと指摘している。 　こういった「読み方」をしながら、「星の王子さま」が「苦悩に満ちた懺悔と贖罪の書であり、自分の死後のフォローを意識したもの」であるのではないか、と言う。

　さて、塚崎幹夫氏の影響を多いに受けている私ではあるが、私なりの「読み方」をしてみたい。「水」というキーワードにこだわった「読み方」をしてみる。私の受ける印象では、「水」というキーワードには深い思いが込められているはずなのだ。

　そのために、

• 星の王子様のリンク集( http://www.slis.keio.ac.jp/~makiko9/prince.html )

から情報を辿り、

• Antoine de ST.EXUPERY:LE PETIT_PRINCE ( http://galeb.etf.bg.ac.yu/mp/mp/pp.html )

から「星の王子さま」-"Le petit prince-のフランス語のテキストを入手した。オリジナルにこだわったわけではない。日本語版も英語版も電子テキストでは手に入らなかったのである。

　さて、単語にこだわって解析をするとなれば、

• 夏目漱石は温泉がお好き? - 文章構造を可視化するソフトをつくる - (1999.07.14)
• 失楽園殺人事件の犯人を探せ - 文章構造可視化ソフトのバグを取れ - (1999.07.22)
• 「こころ」の中の「どうして?」　- 漱石の中の謎とその終焉 - (1999.09.10)

と同じように、WordFreqを使うのが有効だろう。まずは試しに"CHAPITRE"の出現分布を調べてみよう。そうすれば、行数と章構成の対応がわかるわけだ。

行数と章構成の対応

　このように27章と物理行の対応がわかる

　それでは本題の、"'eau"の出現分布を調べることで、「水」の出現分布をwordfreqで解析してみる。

"'eau"-水-の出現分布

　最初と最後に「水」が登場しているのがわかる。このような、物語の「始まり」と「終わり」集中して出現する単語と言うものは、重要な意味を持つと考えるのが普通だろう。冒頭で、水を持たない主人公が、話の最後で水を湛える井戸を見つける。これは、どのような意味があるだろうか。また、王子にとって重要な「守るべきもの」に王子は水を与えていたこと、これらは何を意図したものなのだろうか。

　さて、「水」が出現するのは

1. 50行目付近
2. 300行目付近
3. 1300行付近

の計三箇所である。それは、冒頭の主人公が水をなくしたところ、バラに水をやるところ、王子と主人公が水を探しに行き、見つけるところである。それでは、その出現個所の中から重要そうな部分を拾ってみよう。特に、最後の1300行近辺を集中して考えてみる。ここで、冒頭の数字は、「星の王子さま」岩波少年文庫でのページ数を示している。

• 115 だって、ぼくが水をかけた花なんだからね。
• 124 水は心にもいいものかもしれないな...
• 131 その水は、たべものとは、別なものでした。
• 131 だけど、さがしているものは、たった一つのバラの花のなかにだって、少しの水にだって、あるんだがなぁ...
• 147 星がみんな、井戸になって...そして、ぼくにいくらでも、水をのませてくれるんだ。

　また、他の作品「城砦」の文章も示しておこう(といっても星の王子さまの世界からの孫引きであるが)。

• その人間を解放するということは、彼に渇を教え、また井戸への道を教えてやることだ。
• それら井戸のひとつひとつに、どうしてもたどりつかねばならないようにするだろう...必死になってその井戸をめざさねばならなくなる。
• おまえが水を飲もうと思うとき、....おまえの行為を祈りという意味に化するのである。

　こういった、文章をつなげて読んでいったときに、「砂漠が美しいのは、どこかに井戸をかくしているからだよ...」という言葉は殉教者の言葉に聞こえてくる。「砂漠」が「生」と感じられたり、「井戸の中の水」が「意義」と感じられたりするだろう。また、他の言葉にも聞こえてくる。しかし、それらをひとつひとつ挙げることはしない。

　こういう言葉の意味するものをそれぞれ考え、「かんじんなことは、目に見えない」という言葉をもういちど読みなおしたときに初めて、Saint-Exuperyの「星の王子さま」が私は好きになったのである。その「星の王子さま」の二面性こそ、私が好きな部分である。

　さて、最後に次のような二つの文章を並べてみる。こうすると「星の王子さま」に流れる強い背景・考えを感じるのではないだろうか。

二つの文章

「わたしは、この本を、あるおとなの人にささげたが、....そのおとなの人は、いまフランスに住んでいて、ひもじい思いや、寒い思いをしている人だからである。どうしても慰めなければならない人だからである。... 子どもだったころのレオン・ウォルトに」 「星の王子さま」 献辞

(レオンウォルトに) 「今夜しきりと思い出す人物は今50歳だ。彼は病気だ。それにユダヤ人だ。どうして彼にドイツの恐怖を乗り越えられよう？」 「ぼくがなおも戦いつづければ、いくらかは君のために戦うこととなるだろう。...ぼくは、君が生きるのを助けたいのだ。実に無力で、危険におびやかされている君の姿が眼に浮かぶ。更に一日生きのびるために、どこか貧しい食料品店の前の歩道を、50という年齢を引きずって歩きまわっているきみの姿が、擦り切れた外套に身をくるんで、仮の隠れ家で身を慄いているきみの姿が、眼に浮かぶ。」 「ある人質への手紙」

　やはり、「星の王子さま」は端的に言えば、寓話の形をした遺言(の準備をしたもの)であるのだろう。「星の王子さま」が出版された四日後、Saint-Exuperyは戦うためにアメリカからアフリカへ出発する。

　「星の王子さま」は一つの挿絵と、その挿絵の説明で話が閉じられる。その最後の挿し絵は王子が姿を消した場所を描いたものだ。それだけではない。その「アフリカの砂漠」は、Saint-Exuperyが最後に「戦う兵士」として飛行機で通過し、そして、姿を消した場所でもある。

「これが、ぼくにとっては、この世で一ばん美しくって、いちばんかなしい景色です」

■WEBの世界の「力の法則」　

「ReadMe!JAPAN」と「日記猿人」に見るWEBアクセス数分布

　以前、

• 深夜特急 '99 - HIRAX発ロンドン行きWEBの旅- (1999.09.20)

の中で書いたように、「Webの成長のダイナミクスとトポロジは，物理学の世界のPower(累乗)Lawとして知られている法則に従っている」という面白い話が世の中にはある。これは、「ごく少数のWEBサイトへのアクセス、あるいはリンクが他を圧倒する程の割合を示す。」ということである。「インターネットのほとんどのアクセスというものは、ごく少数の特定のサイトへのものである。」ということだ。宇多田ヒカルの売り上げが演歌の総売上をはるかに超えるという話とよく似ている。実社会でもそういうことは実に多い。

　どうも、マイナー趣味である私には、Power(累乗) Lawというのはいま一つ面白くない話ではあるが、

• InternetEcologies
• http://www.parc.xerox.com/spl/groups/dynamics/www/internetecologies.html
• Paperson small-world networks
• http://www.ncrg.aston.ac.uk/~vicenter/smallworld.html

といった所を眺めていくと、どうやら事実であるようだ。ここらへんのWEBはとても読んでいて面白い。そのせいか、似たようなことで遊んでみたくなった。そこで、今回はその"PowerLaw"、すなわち、「力の法則」について考えてみたい。ところで、本来ここでの意味は"Power"=「累乗の法則」となるが、ここでは「力の法則」としておく。

　まずは、考えるためのデータを採取してることにした。欲しいデータは色々なWEBサイトへのアクセス数である。もちろん、自分のWEBサイトへのアクセスではないのだから、何らかの公開データを探さなければならない。

　そこで、ReadMe!Japan(http://readmej.com/)と日記猿人(http://wafu.netgate.net/ne/)という二つのランキングシステムを用いてみた。ReadMe!Japanは日本語の「読み物」を主体としたWEBランキングである。また、日記猿人は名前の通り「日記」をターゲットとしたWEBランキングである。

　一見、同じように見えるReadMe!Japanと日記猿人のランキングであるが、かなり違ったシステムである。以下に、Readme!Japanと日記猿人のランキングシステムを示してみる。

• Readme!Japan　登録したWEBページに、一日の間にアクセスしたIPアドレスの数。
• 日記猿人　「投票」ボタンを押した人(ブラウザー)の数、一日の間に一人の人(ブラウザー)が同一の日記に対して複数回の投票は行うことが出来ない。

　したがって、Readme!Japanに対して、日記猿人は「投票ボタンを押す」という作業が余計に必要となる。単純に「読まれた数=得票」ではないのである。読者に「投票ボタンを押そう」という気持ちを生じさせることが必要とされるのである。
一方、Readme!JapanはIPアドレスベースであるから、同一のProxyなどを経由したアクセスの場合、何人からアクセスがあろうと1pointである。しかし、読者に「投票ボタンを押す」というような作業は要求されない。

それでは、日記猿人とReadMe!JAPANの得票ランキングの例を示してみる。横軸はランク(順位)であり、縦軸が得票数である。ここでは縦軸・横軸共に線形軸を用いている。

日記猿人とReadMe!JAPANの得票ランキングの例 (線形軸)

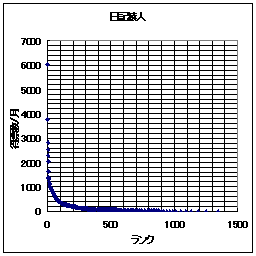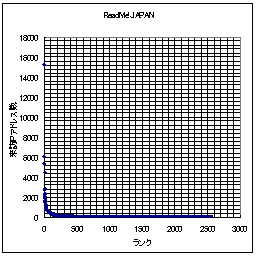　なお、 Readme!Japanは11/30日のものであり、日記猿人は(ほぼ)11月分の得票数分である。
このグラフを眺めてみると、日記猿人とReadMe!JAPAN共によく似ている。なるほど、少しランクが下がっただけで、急激に得票数が少なくなっている。もう、縦軸で言うならば下に張りついてしまっている。「ごく少数のWEBサイトへのアクセス、あるいはリンクが他を圧倒する程の割合を示す。」という「WEBの世界の力(累乗)の法則」は日記猿人とReadMe!JAPANでも当てはまるようである。

　さて、ここまでランクに対して得票数が変化するとなると、グラフの軸は線形軸でなくて対数軸の方が良いだろう。そこで、グラフの軸を対数軸に変えたものを以下に示す。

日記猿人とReadMe!JAPANの得票ランキングの例 (対数軸)

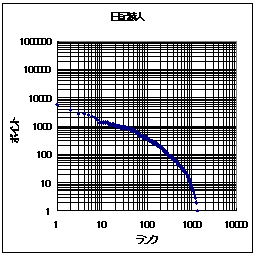　こうすると、日記猿人とReadMe!JAPANのどちらも、

• 上位のランク(例えば、1位から1000位程度まで)では傾きがほぼ1である。すなわち、ランクが一桁下がると、アクセス数も一桁下がる。

というようなことがわかる。まさに、「力(累乗)の法則」である。確かに"Power"である。

　また、ReadMe!JAPANでは、ランクが極めて大きい所では得票数が0に近い。おそらく、その影響と考えられるが、ランクと得票数の関係が直線でなくなっている。

　それと同じことは日記猿人でも言えるだろう、ただし、「ランクとポイントの関係が直線でなくなる」のがReadMe!JAPANよりも早いような気がする。しかし、それは誤差かもしれない。参加数もかなり異なっているので、誤差の可能性が高いと思われる。

　さて、これまでは日記猿人とReadMe!JAPANのランキングの数字を直接用いてきたわけである。しかし、得票数の全く違うものをそのまま比較してもしょうがない。ある程度条件をそろえた上で比較をすべきであろう。そこで、縦軸を正規化して比較をしてみることにした。得票数の合計が1であるような単位に変換してみるのである。

　ここで、横軸はランクのLog_10を用いている。本来、ランク(順位)も何らかの正規化の変換をすべきであろうが、今回はやり忘れた。きっと、頭が疲れているせいである。

　また、グラフを見ればわかると思うが、それぞれについて近似曲線を計算している。

日記猿人とReadMe!JAPANの得票ランキングの例
(得票数の合計が1であるような単位に変換したもの)

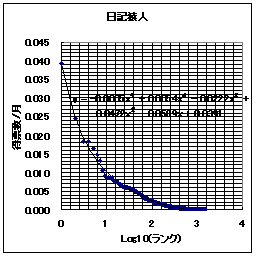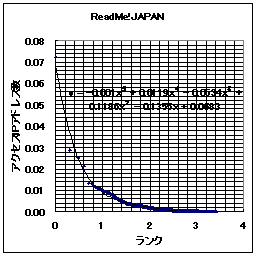　次に、ここで得られた「ランクとポイントの関係」を示す近似関数

• ReadMe!JAPAN 　y = -0.001x^5 + 0.0119x^4 - 0.0534x^3 + 0.1186x^2 - 0.1355x+ 0.0683
• 日記猿人　y = -0.0005x^5 + 0.0054x^4 - 0.0222x^3 + 0.0472x^2 - 0.0589x+ 0.0391

を重ねて示してみる。

ReadMe!JAPANと日記猿人の「ランクとポイントの関係」近似関数の比較

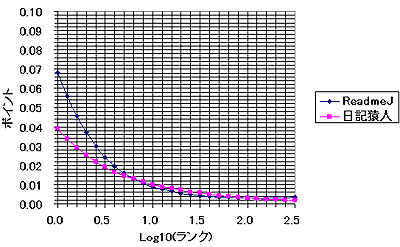R　eadMe!JAPANでも日記猿人でも横軸が2以上(すなわち100位以下)の場所などでは、ほとんどポイントはゼロみたいなものである。すなわち、100位より下のWEBのアクセス(本WEBへのアクセスも含めて)は誤差みたいなものなのだ。何しろ、一位(トップ)のポイントが0.07とか0.04とかなのだ。それは「一位のWEBサイトへのアクセスが全部のサイトへのアクセスの1割弱を占める」ということなのである。20位までのサイトへのアクセスを合計すると全アクセスの50%以上を占めてしまう。これが、恐るべきWEBの世界の"PowerLaw"、すなわち、「力(累乗)の法則」である。

　ところで、日記猿人では上位サイト(すなわち、横軸で0に近いところ)での関係式の傾きがReadMe!JAPANよりも小さい。すなわち、上位サイトの得票数が拮抗している。これは一体何故だろうか?
私はこの理由を、

• 日記猿人の読者が割と似ている趣味を持っている
• 日記猿人の参加WEBサイトが似たような内容を持っている

ということではないか、と考えている。

　日記猿人の参加WEBサイトが似ており、読者同士が割と似ている趣味を持っていれば(私も含めて)、得票数というのは当然横並びになるだろう。上位サイトにはほとんどの人が見に行き、そしてほとんどの人が「投票」ボタンを押せば、上位サイトはみな同じような得票数を示すことになる、と思うのである。
　それは、違う傾向を示すReadMe!JAPANの中でも、読者層も作者も似ている「Fast&First」と「今日の必ずトクする一言」はとても近い得票数を示している、ということがその根拠の一つである。

　それに対して、ReadMe!JAPANが比較的広いジャンルの「読み物」が集まっているのでそういう現象が見られないのだろう、と考えるのである。しかも、実際には「読み物」ですらないものも集まっているので、なおさらジャンルとしてはバラけている。だから、「WEBの世界の力(累乗)の法則」を素直に反映していると考えるのである。

　私としては、ごく一部のWEBサイトへの集中が生じるのはツマラナイと感じてしまうのであり、「WEBの世界の力(累乗)の法則」はキライである。だからといって、趣味が似た人ばかりというのもツマラナイように思う。うーん、どういうのがツマラナクナイのだろうか?
それはきっと、「色々な趣味の人が色々なWEBへアクセスする」というのが私の好みだ。実現は難しいのだろうけど...いや、そんなことはないか。