2000-10-29[n年前へ]
■「しょんべん小僧」の物理学 
あともう一歩、前に出ろ
以前、- スクール水着の秘密 - 腹の部分のデカイ穴 流体力学入門編2 - (2000.08.24)
「男性にはよくある風景だけれど、女性にとっては未知のミステリアスゾーン」といってもたくさんあると思うが「男子トイレ」というものだって、女性にとっては未知のミステリアスゾーンだろう。
次の絵はよくある男子トイレの一風景だ。便器前のポジションに立つとどうしても目に入る位置にこんな内容を書いたチラシが張ってあることが多い。
「ちょっと待て、あともう一歩前に出ろ。」
 |
もし、その張り紙がなかった場合にはどうなるだろうか?その場合には、下の絵のような事故が発生してしまうのである。実際のところ、ほとんどの公衆便所で見かける風景だ。
 |
そう、便器にロックオンして放水をしたハズなのに、何故かターゲットである便器まで「小便」が届かずに便器下を汚してしまうのである。実にマズイ事態ではあるがよく見かける風景でもある。便器内を狙ったハズの小便が残念ながら目標地点まで辿り着かなかった場合に起きる悲劇である。
もちろん、どんなに飛距離が小さくても、すなわち小便が放水銃の先から真下に垂れてしまった場合でも、便器の顎の上から放水作業を行っていれば何の問題もないわけだ。しかし、世の中の男性達は何故か遠くから狙いたがるのである。先程の、「ちょっと待て、あともう一歩前に出ろ。」という張り紙ではないが、もう一歩前に出て便器の顎の上から放水作業を行いさえすれば良いのではあるが、何故か漢(ここではあえて、漢と書いてオトコと読むことにしよう)達はそれができないのである。
さて、この現象には別に公衆便所でなくても発生するわけで、どこのトイレでも便器の下を汚してしまうことになる。そのため、家庭によっては妻から
はるか古の昔から「男らしさ」のひとつが「立ち小便」でなかったか?、そして「立ち小便」は「男らしさ」の最後の砦ではないのか?という気も私は少しだけしたりするのだが、便器周りを汚しまくる現実の前ではそんな「男らしさ」は2000円札よりも価値がないのである。2000円札ならば喜んで受け取ってくれる人もいるだろうが、便器の下に落ちようとする「小便」は誰も受け取ってくれない。いや、実際のところ小便を喜んで受け取ってくれる人もいるのかもしれないが、少なくともそんな人の数は2000円札を喜んで受け取る人の数よりはきっと少ないだろうと思うのである。
そしてさらに、「男らしさ」が「立ち小便」なら、そんなものイラナイと言われてしまいそうな気もするし、「立ち小便」が「男らしさ」の最後の砦か!?と言われてしまいそうな気も強くするので、ここらへんについての社会学的な考察は追求しないでおこう。
それでも、私は世の中の虐げられている「しょんべん小僧」達のため、そして「男らしさ」の最後の砦を守るために、男子トイレの「しょんべん小僧」達がどうしたら、放水ミスをしないかを物理的に考えてみることにしたい、と思うのである。
さて、便器まで小便が届かないという「放水ミス」はどのようにすれば防ぐことができるだろうか?小便の飛距離を小さくしないためにはどのようにしたら良いだろうか?そのためには、まず小便の飛距離がどのようにして決まるのかを考えなければならないだろう。
下のちょっとリアルな「しょんべん小僧」の放水作業ではないが、小便の軌跡はきれいな放物線を描く。
 |
すなわち、空気抵抗などは無視した場合のピストルの弾と同じく
- 銃筒の先端を出るときの初速度
- 銃筒の角度
銃筒の先端を出るときの初速度 = V0と表すと、小便の飛距離は
銃筒の角度 =θ
a V0^2 Sin[2θ] (aは定数)と表される。この式を見ればθ = 1/2 rad.の時にSin[2θ]が1になるので一目瞭然であるし、また感覚的にも自然であるが、銃筒の角度の方は上向き45度の角度に向けるときに小便の飛距離は最大になる。一方、初速度V0の方は速ければ速いほど、小便の飛距離は伸びる。
それを示したのが、次の図である。「小便の銃筒の先端を出るときの初速度と銃筒の角度を変えた時の小便の飛距離」を示したものだ。
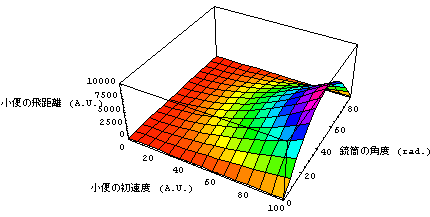 |
すると、便器まで小便が届かないという「放水ミス」すなわち、小便の飛距離を小さくしないためには、銃筒の角度を大きくしすぎたり、小さくしすぎたりしないという知見が得られるわけであるが、そんなことは当たり前だ。誰もトイレで銃筒を真上に向けたり、真下に向けたりはしないのである。先のちょっとリアルな「しょんべん小僧」ではないが、手で放水銃を支持している限り何の問題も無いのである。
つまり、便器まで小便が届かないという「放水ミス」はほとんどの場合「放水銃の角度」のせいではないのである。つまり、「銃筒の先端を出るときの初速度」が問題だったと考えるのが自然である。
それでは、「銃筒の先端を出るときの初速度」はどのようにして決まっているのだろうか?それを大雑把に考えてみたのが次の図である。腹筋で膀胱に圧力Pをかけて、銃筒の先端から小便を初速度V0で放水作業を行うのである。
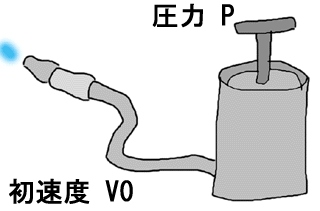 |
ところで、上の絵でポンプとして表した膀胱に圧力Pをかけた場合には、膀胱からb P (bは比例定数)と表せる量の小便が銃筒に送り込まれるものとしよう。その場合、その量の小便が銃筒の先端から単位時間に出るわけであるから、銃筒の先端の口径をAとすれば、
V0 = b P /Aと表すことができる。すなわち、「銃筒の先端を出るときの初速度V0」は腹筋で膀胱を締め付ける圧力Pに比例し、銃筒の先端の口径Aに反比例するのである。
さて、いくら腹筋が強い人であっても腹筋をいきなり締め付けることはできない。つまり、腹筋で膀胱を締め付ける圧力Pというものは徐々に大きくなるのである。
すると一見、「銃筒の先端を出るときの初速度V0」も0から徐々に大きくなる、すなわち、放水作業を開始した最初の瞬間は「銃筒の先端を出るときの初速度V0」= 0であって、小便の飛距離も0である、つまり、便器まで小便が届かないという「放水ミス」が必ず起きるかというと、実はそういうわけではない。
ポンプである膀胱から銃筒の先端までは、ある程度の長さがある。もちろん、その長さは一定ではないのだが、とにかくある程度の長さがある。そのため、小便が銃筒の先端から出る瞬間には、ポンプである膀胱にかかっている圧力Pは0ではないのである。すなわち、膀胱から銃筒の先端まである程度の長さがありさえすれば、「銃筒の先端を出るときの初速度V0」は結構大きくすることができるのだ。もちろん、腹筋を鍛えて、腹筋に急激に力を掛けることができれば、その効果はさらに上がることは言うまでもない。
だとしたら、一般的に便器まで小便が届かないという「放水ミス」は一体何時起きるのであろうか?それは、「銃筒の先端を出るときの初速度V0」を決める膀胱にかかる圧力Pが低下し、なおかつ最初の瞬間と違い「膀胱から銃筒の先端までの長さ」を有効に活用できない、放水作業を終える瞬間である。飛行機でも着陸が一番難しいというが、この放水作業もやはり放水作業を終える瞬間が一番難しいのである。そのため、多くの場合小便達は便器内への着陸に失敗し、便器の下を汚してしまうのである。
しかし、私は「男らしさ」の記念物でもある「立ちしょうべん」を守るために、一つの解決策を考えついたのである。「男らしさ」の最後の砦を守る技術を提唱したいのである。すなわち、「銃筒の先端を出るときの初速度V0」は腹筋で膀胱を締め付ける圧力Pに比例し、銃筒の先端の口径Aに反比例するのであるから、放水作業のラストに膀胱を締め付ける圧力Pが小さくなった、あるいは、膀胱を締め付ける圧力Pを有効に膀胱からの排水に変換できない排水作業のラストにおいて、銃筒の先端の口径Aを小さくしてやればよいのである。そうすれば、「銃筒の先端を出るときの初速度V0」は「銃筒の先端の口径A」に反比例するのであるから、膀胱から出てくる小便の量が低下しても、「銃筒の先端を出るときの初速度V0」を0にならないように維持することができるのである。これにより、放水ミスを防ぐことができるハズなのである。
さて、私は「男らしさ」の最後の砦である「立ちしょうべん」を守るために、このような技術を考えてみたわけであるが、この技術の実証作業は行っていない。果たして、「銃筒の先端の口径A」を自分の意識で小さくすることができるか!?というところに大きな問題点があるような気もするのであるが、それは「男の意地」で克服できると私は信じている。外部から制御するって手もあるのだし。って何の手の話だ、全く。
2000-11-26[n年前へ]
■ブランコの中の∞(無限大) 
なんで一体漕げるのだろう?
公園のブランコというのは、何故かとても不思議な雰囲気を持っている。ホントにうるさいくてたまらないくらいのガキんちょ達が、アクロバットのようなスゴイ技を見せていたりする。それは、まるで上海雑伎団を見ているような気分になる。小さな子がなかなかブランコが漕げず、ブランコの上で宇宙遊泳のように四苦八苦しているのを見ているのも思わず笑ってしまうくらいに可愛らしいものだ。もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。
やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう?口で上手く説明できる人がいるだろうか?
それに、そもそも私たちはブランコを何故漕ぐことができているのだろう?
いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?という手紙で始まるのは加納朋子の「ななつのこ」だが、「何故、リンゴは落ちるのかという謎」と同じく、「ブランコの漕ぎ方の謎」だってとても不思議だ。いつも目にする公園のブランコを、私たちは一体どうやって漕ぐことができているのだろう?
いつだって、どこでだって、謎はすぐ近くにあったのです。
何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。
もちろん、「何でブランコの漕ぎ方が不思議なのさ?」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。
次の図は「ブランコを漕いでる子供」である。
 |
この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか?それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。
だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか?
次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、
- ブランコの動きの中心を向いている軸A
- 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B
 |
ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。
それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。
というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。
ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか? この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか?
 |
「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ!)上がれば、ブランコの速度はもとの速度の倍になるのである!
ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。
もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ!
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。
このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、
- 初期のブランコの速度 = 10
- 重心位置を高くして 10 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- 重心位置を低くして 10 X 1/2 = 10 (何てこったい、速度が半分になっちまったか!)
- 初期のブランコの速度 = 10
- 重心位置を高くして 0 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- そのあとブランコの速度 = 0
- 重心位置を低くして 0 X 1/2 = 0 (0が0になっても全然変わってないもんね!ヘヘン!)
人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。
まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。1万円×2=二万円では1万円しかもうからないが、一千万円×2=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。
もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。
そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね!となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。
というわけで、
- ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
- ブランコが上に行ったときにその姿勢を元に戻す
それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。
というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ
- 何もしない場合
- ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
- ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合
 → ブランコの動きはず〜と変わらない |
ブランコが上にきたあたりで座り込んだ場合  → ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」 |
ブランコが上にきたあたりで立ち上がった場合  → ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」 |
この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。
ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか? それとも、ちょっと考え過ぎかな。
2000-12-01[n年前へ]
■続々オッパイ星人の力学 
胸を揺さぶるパラメータ励振 編
前回、
では、純真でピュア〜な幼心に戻って公園で大きく揺れるブランコの動きを考えてみた。近所の公園でよく見かける、小学生位の子供達が一心不乱にブランコを揺らす景色の中に隠れている科学をちょっとばかり考えてみたわけだ。そして、「ブランコの漕ぎ方の謎」の中には「パラメータ励振」という物理現象が隠されていることを眺めてみた。動きの周期のタイミングに合わせて、パラメーターを変えてやることでブランコの振動を大きくしていたのだった。ところで、公園でブランコを揺らす子供達と同じく、純真でピュア〜なのが生まれたばかりの乳児達である。もちろん、そんな乳児達はまだまだ公園でブランコを揺らすなんてことはできなくて、大きく成長するために母親の母乳を飲んで、そしてただひたすら眠る毎日を過ごしているのである。
そんな乳児の頃の純真でピュア〜な気持ちを、大人になっても持ち続けている人達もいる。そんな純真でピュア〜な大人達は大人になっているにも関わらず、生まれたばかりの乳児と同じくオッパイに惹かれ続けているのである。そして人は彼らをほんの少しばかりの尊敬と沢山の侮蔑を込めて「オッパイ星人」と呼ぶのである。
これまで「できるかな?」では、そんなオッパイ星人達の科学である
を考察してきた(いやもちろん目的はオッパイ星人と闘うためであって、女性を守るためであることはもう一度ここで確認しておきたい)。今回は「純真でピュア〜」をキーワードにして「子供達がブランコを揺らす景色の中に隠れている科学」と同じように、「オッパイ星人の力学」について考えてみたい、と思うのである。
まずは、次に示す「純真でピュア〜」な二つの運動を見てもらいたい。一つは、「純真でピュア〜」な
子供達が公園のブランコを揺らしている時の動きであり、もう一つは「純真でピュア〜」な「オッパイ星人」達が眺めているGカップバストを揺らす女性の胸板の動きである。
子供達が公園のブランコを揺らしている時の動き
| 「オッパイ星人」達が眺めている Gカップバストを揺らす女性の胸板の動き
|
この二つの図をじっと眺めてみると、何か共通点が見えてはこないだろうか?少なくとも、私(純という名前を持つ位だから純真さでは保証付きである)と同じく「純真でピュア〜」な目で眺めてみれば、共通点が見えてくるハズなのである。
「何か、単に両方グニョグニョした動きにしか見えないぞ。」という人、つまり「純真でピュア〜」な目を持たない人もきっと多いことだろう。哀しいことに、この世知辛い世の中ではそんな「純真でピュア〜」な目を持ち続けるのはムズかしいことなのである。そこで、そんな不純な人でも判りやすいように、さらに
- 子供がブランコを動かすときの「子供の上下方向および水平方向の動き」
- 女性が歩くときの「女性の胸板の上下・左右方向ぞれぞれの動き」
重心の上下方向への運動  |  |
そして、こちらが女性が歩くときの「女性の胸板の上下・左右方向ぞれぞれの動き」である。
胸板の上下方向への運動  | 胸板の左右方向への運動  |
こうしてみると、ブランコを揺らす子供の動きと、Gカップバストを揺らす女性の動きが、よく似ていることがわかるだろう。上下方向への運動は全く同じであるし、左右方向への動きはタイミングが違うだけ、つまり位相が違うだけなのである。その位相の違いを実感するためには、
- 時間
- 左右の動き = X
- 上下の動き = Y
 |  |
方向性が逆であるだけで、全く同じであることがよく判ると思う。方向性の違いを除けば、ブランコを揺らす子供の動きとGカップバストを揺らす女性の動きは全く同じなのであって、私はこれら二つの運動の根本原理は全く同じものなのではないか、と思うのだ。もちろん、その原理を「純真でピュア〜な心」である、と言ってしまえばそれで終わってしまうわけなのだが、それでは「科学(?)」ではない。「純真でピュア〜な心」がブランコを動かし、世界を動かし、ついにはGカップバストを動かしているのだぁ、と言えば哲学的(?)ではあるが、科学(?)ではない。いや、そんなのは科学的でも哲学的でもなくて、単なるエロ・エロ・トークだと言う人もいるかもしれないが、そういうことを言うヤカラは「純真でピュア〜」な目を持たない人に違いないのである。少なくとも、「なんて素晴らしいファンタジ〜なんだぁ」という位には言って欲しいのである。
ただ、「ブランコを揺らす子供の動きとGカップバストを揺らす女性の動きは方向性が逆がである」ということは実は面白い考察ができるのである。前回、ブランコの動きを考えた時に、ブランコの効果的な漕ぎ方と方向性が逆の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合 」のシミュレーション計算をしてみた。その結果は、ブランコの振動がどんどん小さくなってしまったのであった。つまり、除振効果が働いてしまうのである。
ということは、である。Gカップバスト(いやAAAカップでも同じであるが)を揺らす女性の動きは、実は揺らしているのではなくて、Gカップバストを揺らさないために最も効果的なのではないだろうか?Gカップバストが揺れ動いてしまってはオッパイ星人はともかく、本人はとても困るわけでそのために実は彼女らは「パラメータ(パラメトリック)励振」という物理現象・科学を応用しているのではないか、と想像してみるのもオツなものではないか、と私は思うのである。
もちろん、ブランコの動きが実は結構複雑であるの以上にGカップバストの動きは複雑である。弾性・塑性・そして様々なブラジャ〜による拘束条件も解明しなければならないだろう。それは実にメンド〜な試みではあるが、きっといつか「純真でピュア〜な心」を持つ学生諸君がその謎を解明するに違いない。「天使のブラによる拘束条件とGカップバストのパラメトリック励振」なんていうタイトルの論文を近日中に目にすることができるに違いない、と私は夢見ているのであった。
2000-12-02[n年前へ]
■ブランコの中の∞(無限大) その4 
mail 実は私は,まじめにブランコの制御を研究していまして,実際にブランコロボットを製作し実験しました.その様子は(リンク)にありますので,ご覧ください. ブランコがなぜこげるかは,数式を使うと簡単に説明できるのですが,直観的に説明しようとするとなかなか難しいものです.物理の教科書にも,これまでなかなかいい説明が載っていなかったので,僕も学生には角運動量の話を使って説明していました.今回,同じ論法で説明されている方を見つけて大変感激しております.次回のパラメータ励振の話も楽しみにしています. < Thank you. jun hirabayashi 「次回のパラメータ励振の話」を読んで失望されていないことを、ただただ願うのみです。ハイ。
2000-12-22[n年前へ]
■子供の科学 
少し前に本屋で「子供の科学」を立ち読みした。末尾の広告に懐かしくもドキドキした。そして、「めざせプログラマ!」がどうなっているのか興味深く読んだ。私の感想としては、私の好きだった「子供の科学」としては失敗だと思う。ファインマン物理学が大学生・高校生のみならず中学生・小学生に見せても良い教科書であるのと違って、少なくともこの連載は「子供の科学」向きではない。別にこの連載の内容自体が悪いなんていう資格はとてもじゃないが私には無いが…。

