1998-11-29[n年前へ]
■鴨川カップルの謎 
そうだ、京都、行こう
京都の風物詩の一つに「鴨川カップル」がある。京都を流れる鴨川の川縁に、カップルが等間隔に並ぶ現象である。鴨川の三条大橋から四条大橋までがその舞台である。この鴨川カップルについては、いくつかの性質が知られている。
- 基本的にはカップルらは等間隔に座る。
- 暗くなるに従い、カップル間の間隔が狭まる。
- 電灯の近く、すなわち、比較的明るいところではカップル間の間隔は広がる。
- 夏はカップルの間隔が狭まり、冬はカップルの間隔が広がる。
- 夏はカップル数が多く、冬は少ない。
- 男性が連れ立って、しかも何人かで座っていると、その周りにはカップルはなかなか座らない。
 (四条大橋の上から撮影) |
 |
 |
(この後、1999.05.04午前中に撮影した画像も示す。午前でもあるにも関わらず、上の時より密度が高い。もちろん、夜の密度の高さはこんなものではない)
 |
今回の目的は、「鴨川カップル」のこのような性質はなぜ生じ、そこに効いているパラメータを実測することである。
まず、性質2,3(暗くなるに従い、カップル間の間隔が狭まる、電灯の近く、すなわち、比較的明るいところではカップル間の間隔は広がる)より、明るいと隣のカップルと離れようとする力が大きくなると予想される。また、カップル同士が離れようとする力、斥力、のバランスにより性質1(基本的にカップルらは等間隔に座る)が形成されていると考えられる。
性質3(夏はカップルの間隔が狭まり、冬はカップルの間隔が広がる。)の季節による間隔の違いは性質4のカップル数の違いから来ているのかもしれないし、それ以外の何らかのパラメータがあるのかもしれない。性質4(夏はカップル数が多く、冬は少ない)はやはり「寒さ」のせいであろう。京都は本当に寒い。いくらアツアツのカップルとは言えども、寒いものは寒い(多分、想像だが)。当然、建物の中でのデートとなるだろう。自ずと、鴨川カップルは少なくなる。
性質5(男性が連れ立って、しかも何人かで座っていると、その周りにはカップルはなかなか座らない)については、「男性の群れ」というのは普通のカップルに比べて非常に強い斥力が働いていると考えられる。この性質5に関しては、私の実体験を持って語ることができる。私と友人連中が鴨川の川岸に近づくと、座っている鴨川カップルが離れていく、という経験を何度もしたことがある。やはり、強い斥力が働くのだ。
計算は全てMathematica3.0を使った。計算の例をMathematicaのNotebookで示す。また、計算の考え方を以下に示す。
 | 鴨川の川縁を真上から見た所。画面上部が鴨川。画面下部が歩道。画面中央に街灯がある。そのため、画面中央が一番明るい。 |
 | カップル達はこの辺りに座る。 |
 | 対称性を考えて、画面の左半分のみを考える。また、赤い線上にカップルが座るものとする。 |
 | その線上の明るさを模したもの。X=100の所が街灯の直下とする。 このような明かりに照らされた状態で、カップルが照らされているとする。 |
 | 100m内にカップルが5組として方程式を解くとこうなる。棒グラフの先端の位置がカップルの座っている位置を示している。1組目は0m地点、5組目は100m地点、すなわち、街灯の直下である。 明るい所ではカップルの間隔が離れているのが判ると思う。 カップルの居心地(隣のカップルの存在感=隣のカップルの明るさ/距離)はいずれも、8という値である。カップルの居心地指数は少ないほど快適であることを示す。 |
それでは、条件を振ってやってみたい。上からだんだん暗くなっていく。鴨川の半日である。また、カップル数はいずれも100m辺り5カップルである。
 |  |  | 20 |
 |  |  | 16 |
 |  |  | 10 |
 |  |  | 8 |
 |  |  | 6.4 |
昼間はカップルが等間隔であり、夕方になり、街灯で照度分布ができると、カップルの間隔も分布ができている。といっても、そういう条件で解いているのだから、当たり前だが。
また、カップルの居心地は暗くなった夜の方が快適であるのがわかると思う。それは、カップルの様子を見ていても、その通りであると思う。しかし、快適であるからといって、カップルが何をやってもいいという意味ではない。そこは、はっきりしておきたい。
今回は、カップル数を全て同じにしたが、逆に同じ居心地指数であるという条件下で解けば、夜の方がカップルが多いという性質も再現できる。これらの計算モデルと実験を比較していくことにより、鴨川カップルの性質を実証していくことができるだろう。なお、今回は計算の簡単のため、男性連れの効果は組み入れていない。また、いつかもう少しまともな計算をしてみたい。
計算を行った感想だが、実に不毛な計算であった。気が向けば、モンテカルロシミュレーションによる鴨川カップルの検証も行いたい、と思う。が、気が向く日はきっと来ない。
1998-12-28[n年前へ]
■本歌取 1998 
1999年の夏休み
まもなく、1999年だ。1999年というとノストラダムスも有名だが、結構好きな映画に「1999年の夏休み」というものがあった。これを振り出しにして、双六のように考えてみる。
「1999年の夏休み」
金子修介監督の映画だ。不思議な雰囲気の映画だ。原作は萩尾望都の「トーマの心臓」である。そのまた元を辿ると、同じく萩尾望都の「11月のギムナジウム」に辿り着く。つまり、萩尾望都「11月のギムナジウム」 -> 萩尾望都「トーマの心臓」 -> 岸田理生(脚本)「1999年の夏休み」となる。-> 金子修介(映画)「1999年の夏休み」
これは、ある本歌に対して、それを翻案したものが連なっているように見える。本歌取が連なった連歌に見える。だから、それぞれ単独で楽しんでもいいが、どのように変わっていったか、などを楽しむのもいい。
「1999年の夏休み」については
「AngelHouse」( http://www2s.biglobe.ne.jp/~sgsc793/index.htm )
「こどものもうそう」( http://www.asahi-net.or.jp/~IH9K-YNMT/ )
などが詳しい。
 |
この中で、薫という登場人物が登場するが、エヴァンゲリオンに出てくるカヲルはこれに影響されているのではないか、という話が先のWEBに出ていた。底が浅いTVに興味はないが、最後の方で登場する人物の名前が「薫」というのは源氏物語の昔に溯る。それは、日本で初めての物語からの伝統なのである。源氏物語の本歌取といっても良いだろう。「薫」という名前を持つ人物を考える際には、源氏物語の「薫」の役割を意識するべきである。最後に物語の全てを背負い、繋げていく役割を背負うのは「薫」なのだ。この本歌取を意識する読み方は、記号論に通じる。
同じ「薫」が登場するミステリィというと、栗本薫の作品群があるが、特に栗本薫の「猫目石」を読む際には源氏物語の「薫」を意識しなければ意味がないと思う。また、ミステリィ作家で「薫」の名前を持つ人は多い。
- 北村 薫
- 栗本 薫
- 高村 薫
「1999年の夏休み」と同じ金子修介脚本監督の映画として、「毎日が夏休み」がある。こちらは、大島弓子が原作だ。この場合は
大島弓子「毎日が夏休み」 -> 金子修介(脚本)「毎日が夏休み」 -> 金子修介(映画)「1999年の夏休み」
となる。
次に、深津絵里繋がりで(ハル)に移る。
(ハル)
深津絵里はこの映画にも出ていた。 オープニングの雰囲気は「1999年の夏休み」に似ている。どちらも、映画の重要な要素である画像を(ある意味で)使わず、表現をしているというのがいい。登場人物も非常に少ない。表現は制限をかけてこそいいものができると思う。完全に自由な中にはなかなか良い物ものは生まれない。それは、選択肢が増えすぎると、人は良いものを見つけるのは困難だからかもしれない。この映画の内容はパソコン通信関係だ。
 |  |
深津絵里の眉毛はまだ太くて良い。
HOME-TOWN EXPRESS
JR東海のCMというとクリスマスエクスプレスの印象は強いが、第二回目の牧瀬理穂の回しか覚えていない人も多い。しかし、第一回目の深津絵里が演じたHOME-TOWNEXPRESSのクリスマスバージョンが一番良かった。HOME-TOWN EXPRESSはその他にも良いものがたくさんあった。クリスマスエクスプレスになって第二回目の牧瀬理穂の回は、「最後にプレゼントを持って柱の後ろで恋人を待ち、その向うに恋人がいる」ところなど、第一回目の回に対する返歌にも見える。JR東海とくると、萩尾望都関連で「半神」の夢の遊眠社のステージをCMに使っていたものもあった。これなども連歌であり、本歌取の繋がったものである。
ブラッドベリ「霧笛」 -> 萩尾望都「霧笛」 + 萩尾望都「半神」 -> 野田秀樹「半神」 -> JR東海「もっと私 CM」
となる。
 |  |
| HOME-TOWN EXPRESS 1988 帰ってくるはずの恋人がホームに降りてこない。と、思うと柱の向うからプレゼントを持った恋人が現れる。 | 「そんな音をつくってやろう...」 |
最近、NODA MAPの「半神」に深津絵里が出る、と聞いた。これで、深津絵里を狂言回しとして、物語は一周したことになる。
そういえば、深津絵里は「虚無への供物」のTVドラマにも出ていた。あのTVを見た人に、原作の「虚無への供物」の面白さがわかるだろうか...
虚無への供物といえば、連歌はこうなる。
中井英夫「虚無への供物」 -> 竹本健二「匣の中の失楽」
というわけで、「匣の中の失楽」を読む前には「虚無への供物」を読まなければならない。「虚無への供物」の中の「どちらが現実で、どちらが架空の世界なのか、誰がわかる?」という訴えを、そのまま展開したのが「匣の中の失楽」である。「匣の中の失楽」に連なるミステリィ物もあるようだが、問題外としておく。
ここ2,3年は、まるで「虚無への供物」の舞台のような年であったように思う。何が現実で何が架空なのか。
1999-05-23[n年前へ]
■HooPoディスプレイの謎 
夢の扉が開かれる
ビジネスショー'99に行った。そこで、面白いものを見かけたので紹介したいと思う。
まずは、NTTのブースである。下の写真では判りづらいだろうが、色々な画像と文字が立体的に(奥行き情報を持って)すばやく映し出されているのである。
 |
映像が立体的になった瞬間は「まさかレンチキュラー方式?」などと考えてしまったが、
奥行きに2段階しかないことに気づくと(映像の変化が激しく、気づきにくかったのだ)、謎は解ける。一番置くに大きなディスプレイがあり、その前に半透明のシートがあり、そのシートに対して前方からプロジェクターで前景を映し出しているのである。なかなか面白そうなので、後でじっくり観ることにした。
次の面白いものは、以下である。HoroProディスプレイという名称である。
 ディスプレイが透けているのがわかるだろうか?ITEM-16というのは後ろの壁である。 |
アオリの調整などはどうしているのだろうか?そういった機能を内蔵するゾーンプレートのようなものなのだろうか?これは実に面白い活用方法がありそうだ。
NTTもHoloProも簡単なタネを持つ科学おもちゃであり、見ているととても楽しい。どういったタネであるかを考えるのはミステリーを解くようで面白い。
.
.
.
さて、それでは席をちゃんと確保してNTTのブースを見てみることにしよう。こちらは、キーワードといい、演出といい、実に私好みだった。ラストなど感動してしまった位だ。
 「夢の」扉が開かれる。 |
 色々な映像が映し出され、カウントダウンが始まる。 |
 始まるといきなり映像に奥行きが生まれる。 |
 ディスプレイとスクリーンの中央が照らされ、そこに人がいたことがわかる。 |
 輝きながら、スクリーンが揚がる。 |
この緞帳が揚がる瞬間というのは実に気持ちがいい。コンサートでも舞台でも緞帳というのは現実の世界と架空の世界の間の「扉」である。それを開けるということは、すなわち、架空(今回は夢か)の世界へ入っていくことに他ならない。
 ここからメインのプレゼンが始まる |
 プレゼンが終わり、スクリーンが下る。そして、キーワードが前後に映し出される。 |
 周囲が明るくなり、これまで登場した人物達が |
 登場人物の前後を縦横無尽にこれまで使われた映像、 |
これまで登場した人物達は、未だスクリーンの向こう、「夢の扉」の向こうにいるのである。
 「夢の扉」を開く原動力、それは...と始まる長い台詞が続く。 |
もちろん、その瞬間にスクリーンがあがるわけだ。
 スクリーンが揚がり、役者が並んでいる。 |
「扉」の向こうで演じられていた「夢」がすでにここにある、ということを端的に示しているのである。夢の世界はスクリーンの向こうにあるわけではない、夢の世界はもうここにある-「夢の扉」は開かれた-ことを強く示すものだ。
最後の「夢の扉を開く原動力、それは..」.の後につづく台詞も結構良かった。役者と製作者達に拍手をしたい。
1999-12-16[n年前へ]
■スキー場の特殊相対性理論 
ジャンプの飛距離は何メートルだ?
突然ではあるが、HIRAX.NETのドメインレコードを調べてみると、
Record created on 16-Dec-1998.となっている。自分のドメインのレコードをわざわざ調べたのは、一体いつ取得したのか私自身が忘れてしまったからである。何しろ、「できるかな?」は当初異なる場所での二本立てで公開していたため、私の記憶がごっちゃになっているのである。あと各回の公開順序も実はかなりシャッフルされている。そのため、完全に忘れていたのである。
「できるかな?」はHIRAX.NETのコンテンツの一部である。しかし、HIRAX.NETの誕生日よりも、「できるかな?」の誕生日の方が実は早い。
で書いたように、「できるかな?」はすでに満一年を迎えていたわけである。そしてやっと、本日でHIRAX.NETも満一歳になったわけだ。何はともあれ、目出度いことである。子供の頃やらされた「ドリル」でも3日も続かなかったのに、1年続くとは、正に奇跡である。奇跡はそうそう続かないような気もするが... さて、関係ない話はここまでである。今回の舞台は万座温泉だ。なぜなら、先週末私は万座温泉でスキーをしていたからだ。何故だか理不尽な話しではあるが、私は万座温泉でローレンツ収縮を考える羽目になったのだ。もう少し正確に言えば、スキー場で特殊相対性理論を考える羽目になったのである。(先に断っておくが、私はトンデモ話をマジメな顔で言うことが多い。)
 |
話の発端はスキーに行く前に遡る。職場の今年の新入社員であるタカノリ君(仮名)とスキーの話をしていた。彼は秋田出身であり、子供の頃からスキー三昧の生活をしていた。大学に入り京都へ行ってからは、スキーをやる頻度は下がったが、チョコチョコ行ってはいたという。
そのタカノリ君(仮名)と話していると、彼はさりげなくこう言った。
「10m位のジャンプはよくするスよ。」10mである。2mの身長の人の5人分である。それは、スゴイ。
「えぇ、本当かぁ〜〜」
「いやぁ、そんなのよくやることじゃないスか?」
今回のスキー&温泉旅行は職場(と何故か競合他社)の人達30人程で行った。ほとんどの人は、割にスキーは好きな人が多い。従って、スキーも上手い人が多い。その人達に囲まれながら、タカノリ君(仮名)は断言した。
「6,7mは簡単だけど、10mってスゴイなぁ。」タカノリ君(仮名)、ただ者ではない。
「本当かぁ〜〜」
「えっ、だってただ飛ぶだけじゃないっスか。」
そこで、スキー場でその確認をしたわけである。場所は万座プリンスゲレンデの下部である。リフトとコースが交差する辺りに、ジャンプできる場所があったのだ。そこで、彼は軽く滑り出し、力一杯ジャンプした。
果たして、タカノリ君(仮名)は何メーター飛んだのであろうか? それとも、ただのホラ吹き男爵であったのだろうか?
ところが、その答えをすぐに書くわけにはいかないのである。なぜなら、タカノリ君(仮名)がジャンプをしてみせた時に事件は起こったのである。
「どうスか!10mはいったんじゃないスか!」
「3,4mしかいってねーぞ!おイ!」
これは、一体どうしたことだろうか? しかも、会話はまだ続くのである。
「何でっスか!軽く1秒は宙に浮いてたっスよ!」ますます不思議なことに、時間感覚すら違っているのである。一体何が起こっているのだろうか?
「そんなことはねぇぞ!コンマ数秒だろう!」
私はここで気づいたのである。観測者の間で時間と空間の不一致が生じているのであれば、ここはもちろんアレの登場である。アレと言えば言うまでもない、もちろん特殊相対性理論である。
そう、万座温泉スキー場ではローレンツ収縮を実感することができるのである。「スキー場でジャンプする」という現象を考える際には、「スキー場におけるhiraxの特殊相対性理論」を導入しなければならないのであった。
それでは、簡単に「スキー場におけるhiraxの特殊相対性理論」を説明しよう。今回、生じている不思議な現象は以下のようになる。
登場人物
- タカノリ君(仮名) 速度vでジャンプをしている。
- 観客 静止している。
| タカノリ君(仮名) | 観客 | |
| 飛んだ距離 | 10 | 3 |
| 飛んでた時間 | 1 | 0.3 |
つまり、速度vで飛んでいるタカノリ君(仮名)の感じる空間や時間といったものは、静止している観客に比べて、いずれも3倍程度に膨張しているのである。
通常の世界で生じるローレンツ収縮は、速度vで移動している観測者の空間軸も時間軸も
![]()
倍縮むのであるが(ここでは光速c=1の単位系を使用している)、
であるが、「スキー場におけるhiraxの特殊相対性理論」では、速度vで移動している観測者の空間軸も時間軸も静止している観測者に対して、逆に![]()
倍に延びてしまうのである。もし、ミンコフスキーの時空図を書いて確認しようとする人がいるならば、座標軸の傾きの変化も通常のローレンツ変換と逆に考えてみてもらいたい(その延長で考えていくと、矛盾があるというご指摘メールはノーサンキューである。)。
さて、そもそもローレンツ収縮は、マイケルソン - モーリーの実験結果(エーテルの影響が検出できない)を説明し、なおかつエーテルの存在を認めるために立てられた。それは、「運動体はすべてその運動方向に収縮する」という仮説である。その仮説を理論的に完成させたのが、アインシュタインの特殊相対性理論である(考え方としては根本的に異なるが)。
今回の話の中で「エーテル」に変わるのは、「空気」だろうか? いや、違う。私はむしろ、速度そのものであると、考える。つまり、特殊相対性理論と同じである。スピードを出して飛んでいるという感覚、速度が与える感覚の変化、すなわち速度そのものが、「スキー場におけるhiraxの特殊相対性理論」を要請するのである。
今シーズン、スキー場でせっせとジャンプをする人がいるならば、ぜひ「スキー場におけるhiraxの特殊相対性理論」について考えてみてもらいたい。
このWEBへ来る人の中で、同時期に万座温泉スキー場にいた人はいるだろうか?12/11.12に万座温泉スキー場のプリンスゲレンデの下部でジャンプにいそしんでいたのが、私達の一行である。そして、その中の一人(ショートスキーでせっせと飛び跳ねていたヤツ)はこんなことをずっと考えていたのである。
さて、実際のタカノリ君(仮名)の飛距離がどの程度であるか知りたいと思う人も多いだろう。オマエらの主観的な評価でなくて、実測定した距離を教えろと思う人も多いに違いない。
「絶対的な基準など存在しないから、そんなことは私はわからない。」と言い放ちたいところだが、タカノリ君(仮名)の名誉のために書いておく。彼が飛んだ距離は、2m弱のスキー板で4本分はあった。実は、タカノリ君(仮名)の基準が一番正しかったのである。彼は、「やるときはやる有言実行の人」なのであった。
1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
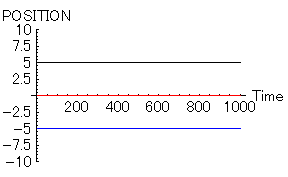 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
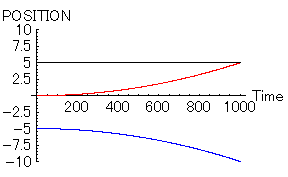 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
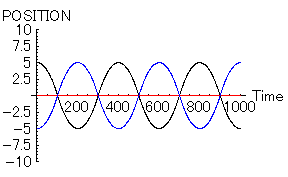 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
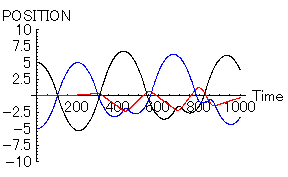 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)