1998-01-08[n年前へ]
■Photohoの乱数プラグインを作成する 
「2項分布のムラについて考える」の関連して、Photoshopの乱数プラグインを作成したのでメモしておく。 PhotShopはとても便利なソフトである。画像を取り扱うにはトップクラスと言っても良い。あえて、難を挙げるならば8Bit階調が基本という所である。もちろん、12bit階調なども扱えるのは知っているが、基本機能とは言えないと思う。
しかし、PhotoShopで凝ったことをしようとすると、Pluginを作らざるを得ない。PhotoShopでPluginをつくるには2つのやり方がある。それは、
- Adobe提供のPlugin SftwareDevelopmentKitを使ってPluginを作る。
- FilterFactoryを使ってPluginを作成する。
今回はランダムノイズをつくるためのプラグイン作成が目的である。その程度であれば、FilterFactoryを使うのが簡単で良い。
 | まずは、FilterFactoryを使う。 |
まずは、Redチャンネルにのみ乱数を与えるものをつくる。以下がそのパラメータである。
 | たった、これだけである。 Redに乱数を与え、Green,Blueのチャンネルには0を与える。 |

もうひとつ、各色に乱数を与えるプラグインのサンプル画像はこのようになる。

さて、試しに使ってみる。1000x1000ドットのランダムノイズ画像を作成してみる。その画像はここに載せるには大きすぎる。そのため、その一部を左下に示す。その画像に対して各領域10x10の100ドットで平均し、100x100に変換した画像を右に示す。詳しくは「2項分布を考える」を見て欲しいが、100ドットで平均したくらいではフラットにはならない。それどころか、有限のいくら広い範囲で平均しても正確にはフラットにはならない。もし、フラットになるのであれば、それはランダムな2項分布ではない。もちろん、PhotoShopの丸め誤差とかの話は別にしておく。また、「2項分布を考える」の際は1次元の1成分データであったが、今回は2次元3成分データである。そのため、人間にはよりフラットに見えにくい。相対的な色差に対しては人間の目は敏感だからである。
 |  |
今回の例も「2項分布の特性:どんなに広い領域であっても、領域中の平均が一定でない」の当然の結果である。仮に、ある広い領域中の平均が一定であるような確率過程を用いればこのようなことは生じない。もしも、そのような確率過程に基づくものがあったら、部分部分はランダムに見えても、広い領域ではフラットに見えるのである。
1998-12-20[n年前へ]
■カラオケ採点機の謎? 
夜空ノムコウ (86点)
カラオケに行くと、必ずといっていいほど、カラオケ採点機(機能)がある。カラオケ採点機というのはどういう基準で採点しているのだろうか。「今のけっこう良かったのになぁ」という時でも、60点位であったり、「おいおい、今のは別の曲だろう」というような時でも、90点台だったりする。もちろん、カラオケ採点機なんて、たいしたことはしていないだろうとは思っているのだが。
まずは、採点機の評価と人間の主観評価の違いを調べてたい。
実験条件は次の通りである。
- 歌った人:A氏、B氏
- 人の主観評価として採点した人:A氏、B氏(最初の2曲はB氏のみが評価した)
- 人の主観評価:5点満点
- カラオケのメーカー:セガのカラオケ
ちなみに、これがそのカラオケの機械とカタログである。
 |  |
それでは、これが結果である。
カラオケをやっている時の実感では、カラオケ採点機の評価と人による評価は全然違うという印象があった。しかし、グラフにしてみると、このようになる。このグラフ中では水平軸が人の主観評価を示し、縦軸が採点機の評価を示している。
 |
人の主観評価が高いほど、採点機の評価も高くなっているのがわかる。また、人の主観評価においても、採点機の評価においても、A氏よりもB氏の方が点数が高い。A、B両氏とも最初の一回目において、人の主観評価よりも採点機の評価がずいぶんと高くなっている。
こうしてみると、それほど人間の主観評価と採点機の評価が無関係というわけではなさそうである。もちろん、誤差は大きいが、「機械にオレの気持ちが判ってたまるかぁ!」と怒るほどのことでもないようだ。採点機の評価基準がA氏とB氏の間でも、違いがあるわけではないようだ。
人による評価と採点機による評価の(推定)対応ラインをグラフにしたものを最後に挙げておく。このグラフからすると、セガのカラオケは
- いまいち = 75点
- まぁまぁ = 80点
- なかなか = 90点
 |
カラオケ採点機については、これで終わることなく、まだまだ調べていきたい。技術的にはどのようなことを行っているのか、各社の技術間で差はあるのか、など色々調べてみたいと思う。
1999-01-10[n年前へ]
■宇宙人はどこにいる? 
画像復元を勉強してみたい その1
知人から「自称UFO写真」というのものが冗談半分(いや100%位か)で送られてきた。その写真はボケボケの画像なので何がなんだかなんだかわからない。そこで、ぼけぼけ画像を復元する方法を勉強してみたい。UFOは冗談として、画像復元において進んでいるのは天文分野である。そこで、このようなタイトルなのである。もちろん、画像復元の問題は奥が深すぎるので、じっくりと時間をかけてみる。今回はMathematicaを使って試行錯誤を行った。
ボケ画像を復元するには、ボケ画像がどのように出来ているかを考えなければならない。そこで、ごく単純なぼけ画像を考えてみる。まずは以下の画像のような場合である。
 |  |
 |  |
画像:1のような点画像が、画像:2のような分布のボケ画像になるとすると、次のような関係が成り立つ。
(式:1) 画像:4 = 画像:3 * 画像:2
画像:1のような点画像が画像:2になるなら、それを参照すれば、画像:3のような点画像の集合がどう
ボケるかは計算できる。つまり、それが画像:4になる。ここで、*はコンボリューションを表している。
よくある信号処理の話で言えば、画像:2はインパルス応答である。といっても、これはごくごく単純な場合(線形シフトインバリアントとかいろいろ条件がある)の話である。まずはそういう簡単な場合から始めてみる。
このようなごく単純な場合には
(式:2) 画像:3 = 画像:4 * (1/画像:2)
とすれば、画像:3を復元できることになる。
そこで、まずは単純な1次元データで考える。下の画像:5のようにボケる場合を考える。ここでは、ガウス分布にボケるようにしてある。
 |
であったが、* すなわち、コンボリューションは
逆フーリエ変換(フーリエ変換(オリジナル画像) x フーリエ変換(ボケ具合))
と表すことができる。つまり、周波数領域で掛け算をすれば良いわけである。
 |  |
それでは、試しに適当な1次元データをつくって、画像:6とコンボリューションをとってやり、ボケさせてみる。
 |  |
逆フーリエ変換(フーリエ変換(画像:9) / フーリエ変換(画像:7))
= InverseFourier[Fourier[Image8] / Fourier[Image6]]; (*Mathematica*)
とやると、次のデータが得られる。
 |
(式:2) 画像:3 = 画像:4 * (1/画像:2)
を見るとわかるが、画像:2が周波数領域で0になる点があったりすると、計算することができない。また、0に近いとむやみな高周波数の増幅が行われて使えない。
そこで、この方法の修正として、ウィーナフィルターなどの最小平均自乗誤差フィルターがある。これにも多くの不自然な条件のもとに計算される(らしい)。しかし、infoseek辺りで探した限りでは、ウィーナフィルターを用いた画像復元の標準であるらしい。
この方法は先の逆変換に対して、次のように変形されたものである。Mathematicaの表記をそのまま貼り付けたのでわかりにくいかもしれない。
Noise ノイズのパワースペクトル
Signal 信号のパワースペクトル
Boke ボケる様子のインパルス応答
Conjugate 複素共役
BokeData ボケ画像
ResData1 計算した復元画像
Boke1 = (Boke^2 + Noise/Signal)/Conjugate[Boke]; (*Mathematica*)
ResData1 = InverseFourier[Fourier[BokeData] / Fourier[Boke1]]; (*Mathematica*)
である。Noise/SignalはS/N比の逆数であるから、SN比の大きいところではインバースフィルターに近づく。また、インバースフィルターの計算不能な点が消えている。
これを使って復元してみたのが、次のデータである。
 |
まずは、ボケのフィルター(PSF=PointSpreadFunction(どのようにボケるかを示すもの)、2次元のインパルス応答)である。
 |
 |  |
 |
その他線形の画像復元法をいくつか調べたが、ウィーナフィルターやインバースフィルターとほとんど同じような物が(素人目には)多かった。そこで、ウィーナフィルタなどとはやり方がかなり異なるものについて、いずれ挑戦してみたい。
関係はないが、ウィナーと言えばサイバネティクスが思い浮かんでしまう。当然、ロゲルギストが連想されるわけだが、文庫本か何かで岩波版と中公版の「物理の散歩道」が安く売り出されないのだろうか?売れると思うんだけど。新書版は高すぎる。
宇宙人はどこにいるか? そういった話は専門家に聞いて欲しい。わからないとは思うが。
さて、ここからは、1999.01.24に書いている。シンクロニシティとでも言うのか、今回の一週間後の1999.01.17に
日本テレビ系『特命リサーチ200X』で
地球外生命体は存在するのか?( http://www.ntv.co.jp/FERC/research/19990117/f0220.html )
という回があった。何とこの回のコメンテーターは先の専門家と同じなのだ。偶然とは面白いものだ。
1999-08-09[n年前へ]
■色を伝える時に、考え忘れていたこと(色弱と色空間 その1) 
We can work it out!
オプトニューズ (1999) No.4の光の話題に三楽病院の岡島修氏が「レーザポインタと色覚異常」という小文を書いている。色弱の人の感じ方とプレゼンテーション(特にレーザポインタの色)に関する提言である。それを読んであることを思い出した。何年か前、Labofinder(Macintoshを科学分野で使うユーザーグループ)でプレゼンテーションについて特集していた発表会だったと思う。どなたかが発表を行った後に、次のような質問があった。
「私は色弱なのですが、プレゼンテーションを行う際に使う色などについて、そのような人を意識して作成されているでしょうか?」
恥ずかしいことに、私はあまり考えたことがなかった。そして、本WEBを作るに際してもそういった点はおろそかになっていると思う。そういう自分自身への反省を込めて、色弱と色空間について考えてみたいと思う。
まずは、色弱に関する情報を調べよう。
- COLOR HANDICAP( http://www.sakuranet.or.jp/~tks/color/text/ )
- からーふぃくしょん( http://sun.endless.ne.jp/users/tanafic/ )
- Dr.MeMeの おめめ講座 (http://www.so-net.ne.jp/vivre/eye/ )
それでは、私なりの理解と考察を始めてみたい。
目に映る明るさって何ですか? - 君は天然色- (1999.07.05)
の回で触れたが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。この内、色(すなわち光の波長方向に関する感じ方)を感じるのは、錐体の働きによるものである。錐体には3種類有り、
- L錐体 -> 赤
- M錐 -> 緑
- S錐体 -> 青
目に映る明るさって何ですか? - 君は天然色- (1999.07.05)
を参照のこと)。それらの錐体に異常がある時に、色弱もしくは色盲が発生する。
| L錐体 (赤) | M錐体 | S錐体 | 先天性色覚異常の分類 |
| O | O | O | 正常 |
| X | X | X | 桿体1色覚 (全色盲) |
| O | X | X | 錐体1色覚 (赤) |
| X | O | X | 錐体1色覚 (緑) |
| X | X | O | 錐体1色覚 (青) |
| X | O | O | 第1色盲 (赤色盲) |
| O | X | O | 第2色盲 (緑色盲) |
| O | O | X | 第3色盲 (青色盲) |
| OX | O | O | 第1色弱 (赤色弱) |
| O | OX | O | 第2色弱 (緑色弱) |
| O | O | OX | 第3色弱 (青色弱) |
この図中でOは正常、Xは欠損、OXは機能低下である。
M,L錐体に関する異常はX染色体劣勢遺伝をする。また、錐体1色覚、および、S錐体に異常がある第3色盲・第3色弱は比較的少ないという。
それでは、これらの錐体に異常があるとどのような色を識別できなくなるのだろうか? 私は先に挙げたようなWEBを読んだくらいの知識がないので、数学的な考察をおこなってみる。現実をよく知らないため、実際の症例とはかなりの違いがあるかもしれない、ということは先に断っておく。
現実の症例の参考としては、岡島修氏の「レーザポインタと色覚異常」中に挙げられているCIEXYZ表色系における強度色覚異常者(第1異常、および、第2異常)の混同色を用いる。その図を加工し、XY色度図を重ねたものを以下に示す。それぞれの図において、白い直線上の色を混同してしまうのである。
 |  |
今回は、通常の(Red,Green,Blue)データを基本として考える。PCなどで表示を行う際に一番よく使うからである。任意のRGBデータをCIEXYZ表色系に直すためには、
WEBページは会社の顔色 -WEBページの色空間を考える2- (1999.04.26)
で用いたハイビジョンTVの色空間を例に用いて、
- X= 0.412391R + 0.357584G + 0.180481B
- Y= 0.212639R + 0.715169G + 0.072192B
- Z= 0.019331R + 0.119195G + 0.950532B
- x=X/(X+Y+Z)
- y=Y/(X+Y+Z)
それでは、通常、第1色盲(赤色盲)、第2色盲(緑色盲)の3種類についてxy色度図の計算例を示してみる。ある錐体に異常が存在する場合に、どのような色空間が再現されるかの計算を行ってみる。通常のxy色度の位置において、ある錐体の刺激を無くした場合に色がどう変化するかを示したものである。であるから、第1色盲(赤色盲)、第2色盲(緑色盲)においては通常使われるxy色度図とは異なるものになる。また、ここで示した色が色弱の人が見ている色という意味でもない。
単純に、ある錐体が得るであろう情報を無くしたときに、情報の識別がどのように困難になるかを確認した、と言った方がいいかもしれない。
また、本来3錐体の波長感度特性はRed,Green,Blueの単波長というわけでもない。しかし、今回は簡単のために、3錐体の波長感度特性はRed,Green,Blueの単波長であるという仮定の元に計算を行っている。そのため、かなり現実とは違う結果になっている。近々、きちんとした計算をするつもりである。
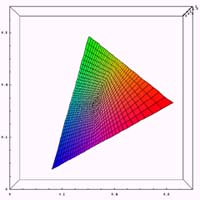 |  | 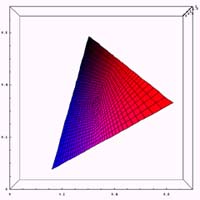 |
ここでは、Z方向(明るさ方向)に対して無視を行っているので、かなりの誤差が存在すると思う。また、計算の中で一つの錐体に異常があるときの、RGBデータの再配分を計算する部分に極めて大雑把な近似をおこなっているので、その部分でも誤差が大きいと思う。
また、Red,Green,Blueの三色により色空間を形成しているため、各点を頂点とする三角形内に色空間は収まることになる。
この計算結果を眺めながら、岡島修氏の「レーザポインタと色覚異常」中に記述されている色弱における混同しやすい色の例、
- 第1色盲
- 赤と黒
- ピンクと青
- 第2色盲
- 赤と緑
- オレンジと黄緑
- 緑と茶
- 青と紫
- ピンクと白
- 緑と灰色
例えば、通常の色空間において赤(すなわち右上)の場所を第1色盲の色空間の中で見て欲しい。黒との識別が困難なのは一目瞭然だろう。また、下の図に示すように、通常の色空間でピンク(1)と青(2)が第1色盲の色空間の中でどうなっているかを見れば、
 | 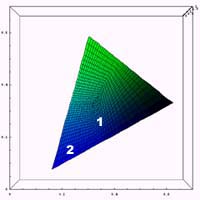 |
これも1と2の識別が困難であることが容易に想像がつく。第2色盲でも同じように見てみて確認して欲しい。
なお、上の図中で中心部が暗くなっているが、それはグリッド線のためであり、本来の色はもっと白っぽい色である。また、今回は岡島修氏の「レーザポインタと色覚異常」中の図と比較するために、CIExy色度図を用いたが、もともとxy色度図は人間の感じ方とは結びつけにくい。いずれ、均等色空間における解析を行うつもりである。また、先に記述したようにきちんと錐体の波長感度特性を考慮に入れた計算をするつもりである。今回はあくまでごく簡単な実験である。
というわけで、今回は色弱の方がどのような色空間を感じているかを考察してみた。今回の話中には色々間違いもあると思う。なにか訂正すべき情報を見つけてくださったら、教えて欲しい。
画像出力に携わる方でこのWEBをご覧になっている人もいるはずだ。色を正しく伝えることを日夜考えている人もいるだろう。しかし、色を正しく伝えることを考えるときに、考え忘れていることはないだろうか? 「正しい伝え方」は、誰にとって「正しい」のだろうか?私達が当然のように感じている色についても、異なる感じ方をする人のことを考え忘れてはいないだろうか?
そういった人は少数だと言われる方もいるかもしれない。しかし、あなたが当然の権利のように享受しているものは果たして全ての人が得ているものだろうか? もしかしたら、その権利を享受している人の方が少数派であるものもあるのではないだろうか?
やることは至極簡単なことだ。技術的に言うならば、人の知覚も「デバイスの一部」として考えた際に、「人の知覚」が数種類あるものとして、異なるデバイス間のカラーマッチングを考えれば良いだけのことだ。もちろん、一筋縄ではいかないだろうが、得られるものの大きさからしたら、やってみる価値はあるだろう。
プレゼンテーションソフト、あるいは数多くのソフトウェアにそういったことをきちんと考えたテンプレートが現れ、WEBサイトの色、画像機器のカラーマネジメントにそういった「全ての人(健常者と呼ばれる人のモデルだけでない)の感じ方まで含めたカラーマッチング」が適用されていく日も必ず来るはずだ。もしかしたら、このWEBサイトに来ている人の中には、今すぐにでもそういうことを始めることが出来る人もいるかと思う。果たして、そんなことが「できるかな?」と思われる人もいるかもしれないが、きっとできる筈だ。
こういったことは色覚に限る話ではないと思う。考え忘れていることは数多くある。できることも数多くある、と私は思う。
1999-09-23[n年前へ]
■MiosoftはApple株でいくら儲けているか? 
価値観は線形なままで
ユング心理学では因果関係が無い偶然の一致を「シンクロニシティ(共時性)」と呼ぶ。いろいろ意見の違いもあるだろうが、私は「シンクロニシティ(共時性)」は結局偶然のせいではなく、世の中の流れの要請による必然なのではないかと思うのである。
と、いきなり訳のわからない話だが、今回の話は「今日の必ずトクする一言」の
ともあれ、webmaster氏のメールのおかげで、株価の値軸が妙に頭に残る最中に、私は「MicrosoftはApple株でいくら儲けているか?」という疑問が沸いて、Appleの株価を見に行ったのである。何しろ、MicrosoftはAppleの大株主である。
 |  |
一見似ているように思える。しかし、よく見てみると軸が違っている。左のAppleComputerの株価変動は対数軸で表されている。「株価表示グラフで値の軸を対数軸にできないか」という言葉が頭にあったせいで気づいたわけだ。そこで、この違いが新鮮で「今日の必ずトクする一言」のwebmaster氏への返信に至ったわけである。
それでは、左のAppleComputerの株価変動をリニアな軸に変換してみよう。
 |  |
印象が全く違う。右の線形軸のグラフは値軸の間隔が等間隔になっているのがわかると思う。それに対して対数軸で表されている右側は上に行くほど間隔が短い。右の線形軸では株価が急激に上昇しているのが実感できる(私は)。株取引的な考察は「対数軸証券グラフのナゾ」の方にあるので、ここでは本題の「MicrosoftはApple株でいくら儲けているか?」に戻る。
さて、このグラフのようにApple株は急上昇中なわけで、問題の「MicrosoftはApple株でいくら儲けているか?」であるが、97/08/08当時の13ドル前後の株価で一億五千万ドル分のApple株を買っていたとしたら、現在は80ドルくらいであるから、およそ6倍。すなわち、一億五千万ドルから九億ドルになっていることになる。うーん、たまらん。800億円近い差が有る(線形的な発想)。
さて、最初の疑問はこれで解決したのだが、わが「できるかな?」でも株価の軸の
- 対数軸
- 線形軸
日頃、実験を行っている時などは
「たかだか一桁の変化だろう。」などと対数軸の感覚に支配されているのであるが、こと経済になると線形軸の感覚に支配されるのである。これは私が貧乏であるからかもしれない。1万円はどんなときも1万円なのである。10万円と11万円の違いも、100万円と101万円の違いも同じなのだ。これが一億円と一億一万円でも同じである。何しろ、そんなお金と無縁なのである。であるから、貧乏な金銭感覚をそのまま線形で延長してしまうのである。「金銭に関する差の感覚」といってもよい。
これは人によっても違うだろう。私と違うブルジョアジーな人であれば、例えば、車を買うときに
「300万円の車を買うから、30万円のカーナビを一緒に買っても誤差みたいなものだ。」という人もいると思う。また、「一億円と一億一万円は同じだ」と言うだろう。これなどは経済に関する対数軸の感覚の一種だと思う。この人は「金銭に関する比の感覚」を持つ人である
さて、こういうことを考えていくと、金持ちの1万円と私の1万円は価値が違うことにいまさらながら気づくのである。私は1万円もらったら大喜びだ。しかし、同じだけビル・ゲイツを喜ばせようと思ったら、九億ドル位は必要だろう。そういうことを考えると、経済社会は実に対数軸である。いや、むしろ世の中が対数軸だと言ったほうが良いだろうか?
今回の話とやはり似て非なる話がロゲリギストの「第四物理の散歩道」の「理解の形式」に述べられているので、興味の有る方は読むと面白いと思う。
さてさて、同じ題材をとってみても経済オンチの私が作る「できるかな?」は「「対数軸株価グラフのナゾ」」とは違い、ずいぶんと変な話になってしまったようである。しかし、それが個性というもの。みんなが同じではつまらない。
ともあれ、価値観に対する評価軸は線形軸の方が良い、と思う私であった。