1998-12-19[n年前へ]
■音階を勉強する 
単音シンセサイザーをつくる
今回は、音階そのものについて勉強をしてみる。世の中には色々な音階がある。いわゆる12音階の中でも、純正調、平均率などいろいろある。12音階でないものもある。どのような音階があって、それぞれどのような音程になっているのか調べてみたい。といっても、まずは7音音階、すなわち、ダイアトニックスケールだけを考える。
参考文献は手元にあった、「音楽の不思議」 別宮貞雄 著 音楽之友社である。なお、江尻氏の音律周波数表、音律について、音律実験(http://www.tg.rim.or.jp/~ejiri/)では色々な音階についての情報を知ることができる。5音階、すなわち、ペンタトニックスケールについての情報もある。同様なWEBサイトととしては「調律法ききくらべのページ」(http://www.top.or.jp/~murashin/index.htm)がある。ARATA氏の「MIDIで古典調律を」(http://www.nifty.ne.jp/forum/fmidicla/htmls/kotenj.html)にもかなりの情報がある。
ここでは、簡単にピタゴラス音階、ツァルリーノ音階(純正調音階)、12平均率だけを考える。
まずは、ピタゴラス音階を作る。Aという基準音を作る。その音に対して振動数が3/2倍の音をEとする。更に、Eに対して振動数が3/2倍の音をBとする。また、Aの振動数に対して、3/2倍の音をDとし、Dの4/3倍の音をGとする。そして、CGの3/2倍の音をCとする。最後に、Cの4/3倍の音をFとする。
各音の倍、あるいは1/2の音のオクターブ違いの音を考えると、結果としてC,D,E,F,G,A,Bのダイアトニックの7音音階ができあがる。このピタゴラス音階は旋律が良く響くという性質がある。よく響くという言い方は誤解を生じるかもしれない。「うまく旋律がおさまる」といった方がいいかもしれない。
| D/C | E/D | F/E | G/F | A/G | B/A | C/B | |
| ピタゴラス音階 | 9/8 | 9/8 | 256/243 | 9/8 | 9/8 | 9/8 | 256/243 |
| ツァルリーノ音階(純正調音階) | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 |
| 12平均率 | 2^(2/12) | 2^(2/12) | 2^(1/12) | 2^(2/12) | 2^(2/12) | 2^(2/12) | 2^(1/12) |
次に、ツァルリーノ音階(純正調音階)は、各音の間の振動数の比を見てもわかるように、和音はよく響く。しかし、旋律として聞いた場合には、必ずしも良いわけではない。しかも、転調はできない。現在、一番使われている12平均率は振動数比をみてもわかるように必ずしも、和音の響きが良いわけではない。しかし、周波数を見てもわかるようにピタゴラス音階とツァルリーノ音階(純正調音階)の中ほどであり、和音の響き、旋律どちらも悪いわけではない。
ただし、1曲の中で厳密に音階が同じというわけでもないらしい。プロの弦楽四重奏などでの演奏では、必ずしも12平均率でなく、曲の中でも意識して音程を変えるという話だ。
また、ツァルリーノ音階(純正調音階)用に曲を作って聞いてみても、それほど良くなるとは思えない。確かにきれいに響くのだが、(私の感じでは)それだけなのである。
セントで表したものも示す。セントは基準音の振動数Nに対して、振動数Mである音を、1200x log_2(M/N) と表す単位である。 セントで表せば、12平均率は当然きりのいい数字になる。
| C | D | E | F | G | A | B | C | |
| ピタゴラス音階 | 0 | 204 | 408 | 498 | 702 | 906 | 1110 | 1200 |
| ツァルリーノ音階(純正調音階) | 0 | 204 | 386 | 498 | 702 | 884 | 1088 | 1200 |
| 12平均率 | 0 | 200 | 400 | 500 | 700 | 900 | 1000 | 1200 |
音階についてあまり長々と考えてもきりがないので、ひとまずここまでにしておく。なにしろ、奥が深すぎる。最後に各音階の周波数表を示す。なお、Cの音はいずれも440Hzにしてある。ここでいうCは音名ではない、階名である。つまり、絶対的な音の高さを示すもの(音名)でなくて、相対的な音の高さを示すもの(階名)である。むしろ、よく使われるドと言ったほうが良いかもしれない。「Aをドにして歌ってみよう」という時の「ド」である。ところで、ドレミファソラシドの語源はどこにあるのだろう?SoundOfMusicがdoeの歌のイメージから"do a dear ..."と鼻歌を歌うことはあるが、語源は一体?次の宿題にしたいと思う。
さて、使用した周波数は全て江尻氏の音律周波数表、音律について、音律実験 (http://www.tg.rim.or.jp/~ejiri/)に記載されていたセントから最初の音を440Hzとし、周波数に変換してある。
| Hz | C | D | E | F | G | A | H | C | |||||||||
| 平均率 12Equal | 440 | 494 | 554 | 587 | 659 | 740 | 831 | 880 | |||||||||
| 純正律 Pure(5-3) | 440 | 495 | 550 | 587 | 660 | 733 | 825 | 880 | |||||||||
| 純正律 Pure(5-3)' | 440 | 495 | 550 | 594 | 660 | 743 | 825 | 880 | |||||||||
| 純正律 PureQ-39(3-5) | 440 | 489 | 550 | 587 | 652 | 733 | 815 | 880 | |||||||||
| 純正律 PureT-71(5-3b) | 440 | 495 | 570 | 594 | 660 | 760 | 855 | 880 | |||||||||
| メルセンヌ純正律 | 440 | 495 | 550 | 587 | 660 | 733 | 825 | 880 | |||||||||
| ピタゴラス律 | 440 | 495 | 557 | 587 | 660 | 743 | 835 | 880 | |||||||||
| 中全音律 | 440 | 492 | 550 | 588 | 658 | 736 | 822 | 880 | |||||||||
| キルンベルガー 第2 | 440 | 495 | 550 | 587 | 660 | 738 | 825 | 880 | |||||||||
| キルンベルガー 第3 | 440 | 492 | 550 | 587 | 658 | 736 | 825 | 880 | |||||||||
| キルン-ヴェルク | 440 | 492 | 552 | 587 | 658 | 736 | 828 | 880 | |||||||||
| ヴェルク 第1技法第3番 | 440 | 492 | 551 | 587 | 658 | 735 | 827 | 880 | |||||||||
| ヴェルクマイスター 第3' | 440 | 495 | 553 | 589 | 660 | 740 | 830 | 880 | |||||||||
| ラモー | 440 | 492 | 550 | 588 | 658 | 736 | 822 | 880 | |||||||||
| ヴァロッティ-ヤング | 440 | 493 | 552 | 588 | 659 | 737 | 826 | 880 | |||||||||
| ヤング 第2 | 440 | 493 | 552 | 587 | 659 | 737 | 826 | 880 | |||||||||
| 43平均律 | 440 | 493 | 551 | 588 | 658 | 737 | 825 | 880 | |||||||||
| 53平均律 | 440 | 495 | 550 | 587 | 660 | 733 | 824 | 880 |
National InstrumentsのLabViewのExample例の中でWindows環境でSoundを入出力するViがあったのでこれを利用する。また、その使用例としてプッシュホンの発信音を出力するものがあった。これを適当にいじって作ってみる。今回は簡単のために単音のみの出力である。いずれ、もうすこしちゃんとしたものを作ってみたい。
作成したアプリケーションをここにおいておく。
Onkai.lzh 1,176kB(配布終了です。)
LabViewのライセンス上、ダウンロード数が50近くになったら削除する。(配布終了です。)
 | まずは、赤丸部分のボタンを押して実行モードにする。 |
 | このように色々な音階を 選ぶことが出来る。 |
1998-12-27[n年前へ]
■Wveletで周期解析をしてみる 
音声・地震などの1次元信号や、画像等の2次元信号処理の解析というのはなかなか面白そうだ。そこで、周期ムラに対してWaveletをかけて周波数解析をする練習をやってみたい。また、短時間フーリエ変換とWaveletの比較もしてみたい。音声・地震などのデータはまた別にやってみることにして、今回は画像データを扱うことにする。ただし、いきなり2次元も何なので、画像データの周期(つまり1次元的な振動)に注目して、解析を行ってみたい。
まずは、「周期ムラのある画像」と「周期ムラのない画像」の2種類の画像を作成する。画像はいずれも数式を用いて作成した。X方向に変化する縞模様であり、表.1のような演算式になっている。一応、2次元画像ではあるが、Y方向にはなんの変化もない。2つの数式を見比べてみると判るが、いずれも2項からなり、低周波数のSinと高周波数のSinからなっている。「周波数ムラのある画像」では、その低周波数のSinの中にさらにSinがあるので、周波数がある周期で変化していることになる。一見、「周波数ムラのない画像」の方でも低周波数のSinの内部にさらにSinがあるように見えるが、0が掛けられているので、実際には存在しないのと同じである。
| 2つのSinからなり、その一方のSinの周期がムラ(一定の周期)をもっているもの。第二項目のSinの内部にさらにSinを入れることにより、周波数ムラを作っている。 | 2つのSin波からなり、どちらの周期も正確なもの。第二項目のSinの中のSinは0をかけてあるので、何ら影響を及ぼさない。 |
そのような数式に基づいて作成した画像を図.1に示す。なお縦軸がX軸であり、横軸がY軸である。図.2(b)では周波数ムラはないが、2つの周波数成分から作成されているため、うねりが生じている。
 | 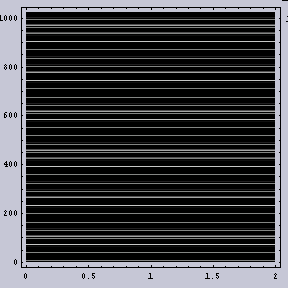 |
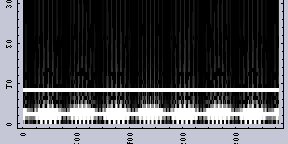
まずは、Wavelet変換である。図.2がその結果である。縦軸が周波数を示している。縦軸の上方向が高周波を示し、下方向が低周波を示している。また、横軸が原画像のX方向である。白は強度が小さいことを示し、黒は強度が強いことを示している。
いずれの画像も2つの周波数成分からなることが一目瞭然である。また、図.2(a):「周波数ムラのある画像」の方では低い周波数成分の方が、さらにある周期で周波数が変化していることがわかる。
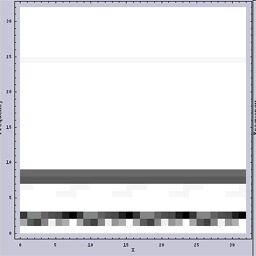 |  |
同じWavelet変換でも異なるFilterを用いてみると、結果は異なる。例えば、図.3がその例である。こちらの方が「周波数ムラ」がどのように生じているかを見るにはいいかもしれない。
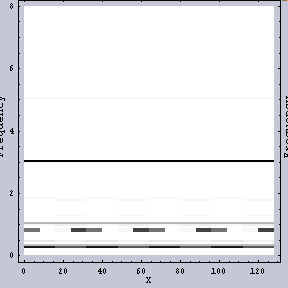 | 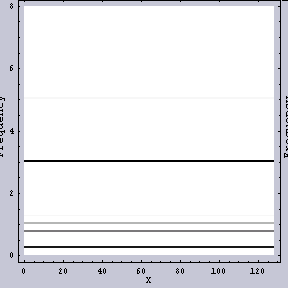 |
それでは、Wavelet変換ではなくて、フーリエ変換を用いて周波数解析を行ってみる。先ほどの1次元データの全領域に対してフーリエ変換をかけてみる。その結果が図.4である。ここで、横軸が周波数を示し、右側が高周波数を示し、左側が低周波数を示している。縦軸は強度である。
このフーリエ変換の場合も、2つの画像が2つの周波数成分からなり、図.4(a):「周波数ムラのある画像」では低周波数成分がぶれているのはわかる。しかし、その周波数ブレがどのようなものであるかまでは、わからない。
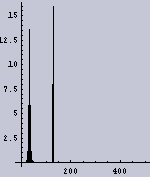 | 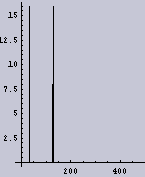 |
なお、単純のためにウィンドー処理はしていない。そのために悪影響は当然出てしまう。
 |  |
単なる全領域にわたった周波数解析と、位置と周波数が同時にわかる解析の違いは非常に大きい。使いこなすのはなかなか難しそうだが....
1999-01-03[n年前へ]
■オシロスコープソフトを作る 
PCを2Ch高性能オシロスコープにしたい
オシロスコープがあると便利だが、家で使うには敷居が高いし、値段も高い。まして、FFTアナライザーがついて周波数解析も行うことができるような機械になると、遊びで買うという値段ではなくなってしまう。そこで、PCを2Ch高性能オシロスコープにするソフトを作ってみたい。
以前、音階を調べた時に、SoundBlaster互換I/Fを使ったLabViewのサウンド入出力のViを使用してみる。目標はとにかくオシロスコープと同じ使い勝手であること、使うのが簡単であること、そして、周波数解析などが簡単に行うことができること、である。入力として、音声入力を使用しているので、たいていのPCで使うことができるし、音声入力マイクが着いているPC(たいていのノートPCは着いているだろう)なら、マイク(あるいは入力端子)を用意する必要すらない。
というわけで、下がそのアプリケーションの画面。
 |
20KHz(ナイキスト周波数で言えば正確には10KHzか)までしか、使うことはできないが、ちょっと使いたい時には便利だ。特に、音声を解析したいならば、必要十分である。上の画面では口笛を吹いて、その音声波形を表示させ、周波数解析を同時に行っている。周波数ピークが表示され、1120Hzであるという表示がされる。
内蔵マイクを使用すると、ただアプリケーションを走らせれば、音声周波数解析が行える。もしも、比較的高性能なマイクがPCに着いているならば、リアルタイム振動解析すら行うことができる。もちろん、マイク入力端子に何らかの入力をすれば、どんな解析もできるわけだが、何の用意もせずにできるというのは便利である。例えば、うるさいデスクトップPCの近くへこのアプリケーションを走らせたノートPCを近づけると、デスクトップPCがなぜうるさいかを簡単に調べることができる。うるさいのは、ハードディスクの周波数なのか、ファンの周波数なのかすぐにわかる。
今回、作成したアプリケーションはここにおいておく。動作させたら、レンジを調整することを忘れずに。
Ocilo.lzh LZH形式 1,259kB (打ち止めです。あしからず。)
LabViewのアプリケーションライセンス上、ダウンロード数は50回までで、その数近くになったら削除することにする。
1999-01-07[n年前へ]
■振動・声紋解析用のソフトをつくる 
PCオシロソフトを高機能にしたい
前に作った2Chオシロ&FFTアナライザーに時間vs周波数グラフの表示機能を付けたい。そうすれば、もしも音声解析に利用するならば、声紋分析もできる。また、振動解析ならば、周波数変化を簡単に調べることができる。こういったものが簡単に作れるのはLabViewの素晴らしい所だ。
このソフトを動かすと、コンピューターのファンやハードディスクの回転数はとても鋭い周波数ピークを持っていることがよくわかる。また、マイクに向かってしゃべれば、声紋分析も可能である。ウソ発見器などにも応用してみたい。
下がアプリケーションを動かした様子である。左上が生波形、左下が周波数vs強度、右上が1Ch目の時間vs周波数分布、右下が2Ch目の時間vs周波数分布である。
 |
測定用の準備は整ったので、このアプリケーションを使って色々な音声解析や振動解析などをしてみたい。ところで、このアプリケーションを作成した所で、ほとんど同じようなソフトの広告を見かけた。
http://www.mcor.co.jp/goods/fft/
上に載っているソフトと同じようなことは今回のソフトを使えばできると思う。また、http://www.mcor.co.jp/goods/fft/にあるソフトの便利そうなところは参考にしたい。
ここに今回作成したアプリケーションを置いておく。
ocilo2.lzh 1,266KB (打ち止めです。あしからず。)
LabViewのアプリケーションライセンス上、ダウンロード数が40本を近くなったところで削除する。
1999-02-26[n年前へ]
■ヒトは電磁波の振動方向を見ることができるか? 
はい。ハイディンガーのブラシをご覧下さい
(1999.02.26)
リチャード・ファインマンの本の中で次のような問題があったように思う。
「偏光板がフィルターが一枚だけある。その偏光フィルターの偏光方向をどのようにして知れば良いか?」
その本の中での答えは、
「物体の反射光を偏光フィルターを通して見てみる。」
だった。ブルースター角で入射した光の反射光は、入射面に対して電場の振動方向が垂直になっている、ということを利用するわけである。
分かりやすいように、偏光フィルターを通してみたガラスの反射光をデジカメで撮影してみる。左が反射光を通すような角度に偏光フィルターを回したものであり、右が反射光をカットするような角度に偏光フィルターを回した場合である。この左の場合、すなわち、反射光が一番通過している角度から液晶の偏光面がわかるわけである。
 |  |
ところで、このようなファインマンが示したような方法を用いなくても、そもそもヒトは電磁波の振動方向を見ることができるのである。以前、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「鳥は太陽の位置、光の偏光パターンを位置のセンサーに使う」という話があった。ヒトも同じく光の偏光方向、すなわち、電磁波の振動方向を見ることができるのである。鳥はどう見えるかは私にはわからないが、ヒトならば自らが実験台になれるので、電磁波振動方向をどう見ることができるか調べてみたい。というわけで、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「近日中にある実験をする予定である」と書いたものが今回の確認実験である。なお、光の進行方向と磁界の振動方向を含む面を「偏光面」、電界の振動面を含む面を「振動面」と呼ぶ。
電磁波の振動方向をヒトが見ると「ハイディンガーのブラシ "Haidinger'sBrushes"」というものが見える。それを知ったのは、いつものごとく「物理の散歩道」からである。網膜に複屈折性があるために「ハイディンガーのブラシ」が見えるのだという。
私はこれまで、「ハイディンガーのブラシ "Haidinger's Brushes"」を見たことがない。いや、正確に言えば意識したことがない。そこで、判別しやすいように直線偏光を用意してやることにした。そこで、東急ハンズで偏光フィルターを買ってきた。
そして、空を見てみる。もちろん、偏光の偏りが強い、太陽を中心にして90度の角度をなす同心円方向である。詳しくは、
- 可視-赤外域での偏光観測による衛星観測手法の開発基礎研究(http://www.mri-jma.go.jp/Dep/sa/Lab1/labt01-s.html)
- エアロゾル観測(http://mars.im.kindai.ac.jp/KISYO/YPROJECT/kansoku.html)
さて、ヒトである私は、空を眺めて格闘すること5分程で、「ハイディンガーのブラシ"Haidinger's Brushes"」がわかるようになった。私が見たハイディンガーのブラシ"Haidinger's Brushes"を示す。
 |
この絵で太陽の方向は右上であり、偏光面は次の絵の青の矢印方向になる。
 |
というわけで、ヒト(少なくとも私は)電磁波の振動方向を見ることができるのである。慣れてしまうと、白い紙を見つめているときなども(条件によっては)見えるようになる。色を扱う人は意識すると面白いと思う。
ところで、偏光フィルターがどういうものか知らない人のために、NotePCの液晶に偏光フィルターを重ねた写真を示す。
 |  |
なぜ、こうなるかわからない方は、
などを参考にして欲しい。液晶ディスプレイの構造がわかると思う。そして、面白いことに気づいた。NotePCの液晶からの光は直線偏光である。ということは、NotePCの液晶にはハイディンガーのブラシが映っているのである。正確に言えば、NotePCの液晶を見ているあなたの視界の中央には、ハイディンガーのブラシが映っているのである。と、気づいてみると確かに見えている。
というわけで、液晶ディスプレイを使用している方はハイディンガーのブラシを見て頂きたい。以下のやり方がわかりやすいと思う。
1.このWindowを最大化する
2.下へスクロールして画面を真っ白にする。
3.液晶ディスプレイ(NotePC)を回転させる。
4.画面(視点)の中央に(視点に対して位置が)動かない黄色いもやが見えるはず。もちろん、回転はする。
液晶ディスプレイやヘッドマウントディスプレイ(HMD)を色々見てみたが、どれにもハイディンガーのブラシは存在していた。視界の中央に不思議な十字架のように現れているのである。現代の液晶技術が負う十字架である。
誰もが、目の前にあるのにそれに気づかないというのも、実に面白い。まるで、「青い鳥」のようである。そして、そういうことはとても多いのではないかと思う。それはそれで面白い話だ。
- それでは、ハイディンガーのブラシをご覧下さい -