1998-11-29[n年前へ]
■"Sanae chan"はもういない 
Sanae chan was fluid in the net news
「大学ノートにさなえちゃんを画いたのに、消えてしまった。」という歌があると聞いたのですが、誰のどんな名前の歌だったか教えて下さい、という疑問がfj.questions.misc辺りで出されたことがあった。
その疑問に対して、
「私も歌った記憶がある」
「ずいぶん昔の歌であやふやだが、大学ノートの裏表紙に、サナエちゃんを書いたの、で始まっていた。」
「それは古井戸の曲だろう。」
「RCサクセションの「僕の好きな先生」と雰囲気がよく似ていた。」
「さなえちゃんが入っているアルバムはどれだろう?」
などと、その人なりの「さなえちゃん」が記事として次々と流れた。その人の記憶の中での歌詞が数多く投稿された。しかし、どれも少しずつ、あるいは、かなり違った歌詞になっていた。時が流れる中で、その人の「さなえちゃん」の記憶が変化していたのである。
それは、今で言うコラボレーションだったように思う。
多くの人がその人なりの「さなえちゃん」を描く中で、「さなえちゃん」の姿が時々見えたような気がした。歌詞の中の「さなえちゃん」の色々な本当の姿が見えたようにすら感じた。その一連の記事を読んでいると、まるで短編小説を読んでいるように、私には思われた。しかも、net news という大学ノートよりも消えやすい一過性のものであるのが、なおさら新鮮だった。
今日急に、もう一度、その一連の記事を読みたくなった。もしかしたら、過去にnet newsで流れた記事をストックしている所もあるかもしれない。

すると、NetNewsArchive(http://mitsuko.jaist.ac.jp/fj/)という所が見つかった。そこで、NetNewsArchive(http://mitsuko.jaist.ac.jp/fj/)で探してみた。見つからないかもしれない、とあきらめていたが、見つかった。ftp://ftp.jaist.ac.jp/pub/news-archive/fj.questions.misc/List-199401にあった。[song]sanaechanというタイトルで始まるスレッドである。
調べる中で、SeagaleMusic Webから歌詞を知ることができた。そのラストの歌詞は、とてもいいと思う。また、面白いことも知った。カトーカズヒロの70年代なつかし音楽談話室(9)によれば古井戸はアルファベットでは"fluid"と書くそうだ。流体、流動体のことである。また、形容詞ならば、流れていく、変わりやすい、などの意味になる。
その歌の中にいた「さなえちゃん」は、「さなえちゃんが消えたの。もう会えないの。二度と会えないの」と歌われていた。"fluid"が必ずそうであるように、newsgroupに流れた記事もすぐに流れていってしまった。news groupに現れた"sanae chan"はもういない。最近とあるマンガで昔あった曲として「さなえちゃん」というのが登場してました。内容はほとんど不明ですが、最後にさなえちゃんは消えちゃうんだそうです。作者の後書きによればこれはマンガの創作ではなく実在する曲らしいのですが、どなたかご存知ないでしょうか?結構はやった歌ですね。「大学ノートの裏表紙、さなえちゃんを書いたの...」で始まる歌だったと思います。非常に短かったような気がします。歌詞は、「大学ノートの裏表紙に、サナエちゃんを書いたの。」で始まる奴でいいのですか。浅田美代子の「赤い風船」の時代ですね。40代の人が知っているはずですね。課長とかに聞いてみたら?えーと、"大学ノートの裏表紙にさなえちゃんを書いたの"という曲でしたか、記憶があります。昔のフォーク全盛期のころの曲で、歌っているのは、すんごく不確かな記憶ですが、"古井戸"ではなかったでしょうか。古井戸の「さなえちゃん」ですね.15, 6 年前(もう少し前かな?)の曲です.大学ノート裏表紙に書いたさなえちゃんが,消えてしまったというただそれだけの曲ですが,なぜかこころに残ってしまふ.古井戸の「ベストアルバム」のCD にはフルコーラスは入っていなかったと思うので,CD で出ているかどうかは知りません.1971年か72年頃に流行った歌で、古井戸の「さなえちゃん」だと思います。確か仲井戸麗市さんと誰かの二人組のグループだったのでは。「♪大学ノートの裏表紙に」鉛筆で描いたため、(うまく描けたのに)いつの間にか(絵が)消えちゃうんだと思います。
# グループ名、メンバーはちがうかもしれません。
# RCサクセションの「僕の好きな先生」と記憶がゴッチャになってます_o_以下はかなり曖昧な記憶なので、そのつもりで読んでください。古井戸の「さなえちゃん」が収録されているアルバムはCD化されていますが、そのCDを外から見たかぎりでは「さなえちゃん」が入っていることは分かりません。他の曲は収録曲として書かれているのですが、「さなえちゃん」だけは、古井戸の意向でわざと書かれていないからです。ただしCDを聞けば、曲自体はLPと同様に収録されています。したがって収録アルバムのタイトルが分からないと、それを探しだすことは出来ません。「さなえちゃん」の入ったアルバムを昔持ってたのですが,なくしてしまったのでタイトルは確認できないのですが,ジャケットは薄暗い色(暗い灰色?,モノクロ?)だったような気がします.なんて古い曲なのでしょう。わかってしまう、自分が悲しかったりして...兄がよく歌っていた曲です。このころ、ガロの”学生街の喫茶店”もはやっていたと思います。歌詞は、 記憶の奥をたどって、 大学ノートの裏表紙に、サナエちゃんを書いたの。 一日中かかって、一生懸命書いたの。 でも、鉛筆で書いたから、いつの間にか消えたの。 大学ノートの裏表紙の、さなえちゃんは、消えたの...
1999-02-25[n年前へ]
■微小4次元計測をしてみたい 
デジタルカメラ、実体顕微鏡、動画の三題話
最近はデジタルカメラ(以降、デジカメと呼ぶ)が大流行りである。実験の記録に使うと大変便利だ。ところで、実体顕微鏡の接眼部からデジカメで撮影するという話題が
の辺りにある。この撮影法の難しさは、デジカメの種類によって違う。例えば、FujiFilmのFinePix700では光軸合わせに結構苦労する。ところが、ソニーの「DigitalMavica(技術者向けのオプション(例えばオシロスコープ・フード)などもあって便利)」ではこの撮影方法はとても簡単である。「Mavica」のレンズを実体顕微鏡の接眼部に合わせるだけで、視野をうまく合わせることができる。といっても、実体顕微鏡にはCCDなどを接続してあることが多いため、単に実体顕微鏡の接眼部をデジカメで撮影するだけでは面白味が少ない。もちろん、高いCCDカメラの代りにメガピクセルのデジカメを使えるメリットは大きいとは思う。
しかし、実体顕微鏡(双眼式)で何が良いかといえば、立体に見えることである。しかし、CCDカメラの接続は一眼式になってしまう。これまで、一つの実体顕微鏡に2つのCCDを接続できるような実体顕微鏡は見たことがない。そこで、接眼部からデジカメ撮影をする方法なら、立体撮影をすることができるので、実体顕微鏡の長所を生かすことができる。
これがそのサンプルである。交差法と平行法の両方を示す。立体に見えるはずである。
 |  |
 |  |
それでは、3次元計測を行ってみる。まずは、マーキングをする。基板上とICチップ上にA,B,C,Dという4つのマーキングを行う。
 |  |
奥行き方向(Z方向としておく)に違いがある場合には、左右の画像でX方向のずれが生じる。そのずれ量を計算してやれば、Z方向の計測を行うことができる。つまり3次元計測を行うことができる。
| 左 | X | Y | 右 | X | Y |
| A | 124 | 33 | A | 133 | 35 |
| B | 13 | 55 | B | 22 | 55 |
| C | 136 | 167 | C | 144 | 167 |
| D | 101 | 100 | D | 99 | 102 |
左右画像の(x,y)の差をとり視差を出す。すると、(A,B,C)とDの間で違いが有り、Z方向の距離が違うのがわかる。
| 左-右 | X | Y |
| A | -9 | -2 |
| B | -9 | 0 |
| C | -8 | 0 |
| D | 2 | -2 |
この結果から、(x,y,z)を描くと以下のようになる。x-y座標上にzの値を書いてある。Dのポイントのみがz方向に近いのがわかる。
 |
もちろん、本来は光学系から係数などを導くのだが、今回は行っていない。大雑把な説明である。また、同じようなやり方で、3次元表面計測も行うことができる。
ソニーの「DigitalMavica」の素晴らしい所は光軸合わせが簡単なだけではない。動画をmpegファイルとして撮影することができる。というわけで、2台買えば実体顕微鏡の画面を立体動画として保存できる。それが微小四次元計測である。
残念ながら、今回は1台しか使えないので、動画サンプルを示すだけである。mpegファイルをgifに変換したものを以下に載せておく。TFT液晶の拡大画面である。映像の終わりで実体顕微鏡の接眼部からカメラを外しているのがわかると思う。
動画サンプル MPEG形式 507kB
動画サンプル GIF形式155kB (上を縮小したもの)
その他関連情報
1999-11-23[n年前へ]
■ミニスカートの幾何学 
32cmの攻防戦
早朝、東名高速で事故渋滞にはまってしまった。仕方がないので、TVを眺めていると、面白い話をやっていた。それは、ミニスカートの丈の話である。何でも、最近の流行はミニスカートの丈が32cmのものであるらしい。女子高生?などが言うには、
「34cmだと長いしぃ。」だから、32cmだと言うのだ。別に、オリンピック選手でもないのだから、ミニスカートの丈の限界まで挑戦しなくても良いだろう、と私などは思ってしまう。しかし、彼女たちはそう考えないらしい。人それぞれである。
「30cmだと下着が見えちゃうしぃ。」
それにしても、スカートの丈が32cmと30cmの間でそんなに、違いがあるものだろうか? 「見える・見えない」を決める分水嶺がその2cmの違いにあるものなのだろうか? 妙に不思議である。 そこで、ミニスカートの幾何学について考えてみることにした。題して「32cmの攻防戦」である。
何より先に確認しておくが、私は今回は科学的好奇心で動いているのである。そこに、一点の不純な気持ちも存在しないことを、ここで確認しておく。いや、むしろ、女性のためのミニスカート理論の構築を目指しているといっても良いかもしれない。といっても、信用されないとは思うのであるが...
 |
さて、先のTV番組によれば、腰からスカートの先までの長さを「スカートの丈」というらしい。また、先のTV番組により、「腰から下着の一番下の部分(股下を計るときの一番上)までの長さが大体25cmである」という重要な情報を得ることができた。
それでは、解析を始めてみよう。以下に、今回考えた「ミニスカートの幾何学」を示す。なお、今回使用する長さの単位は全て(cm )である。
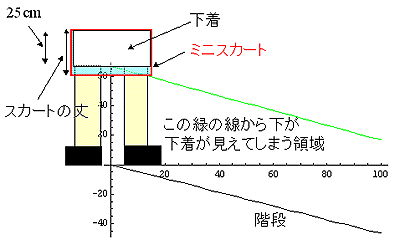 |
まず、階段の途中に立つミニスカートを履いた女性の下着中央部分とミニスカートの最下部を結ぶ直線を考える。この線よりも下が、下着が見えてしまう領域である。もちろん、階段の下には潜り込めないわけであるから、その線と階段で囲まれた領域内から見た際に下着が見えてしまうわけだ。その線のことを「下着防御ライン」と呼ぶことにする。
さて、ミニスカートの形状を考えよう、スカートの丈はもちろん入力条件としてわかる。すると、足りないパラメータは幅である。そこで、ヒップ周りが88cmとしてスカート中央から端までの長さ(rcm)を求める。2πrが88cmであるから、
r = 14cmとなる。
また、駅などの階段というと25度位だろうか。30度というとかなり急な階段である。湘南通商の階段とか急な階段は色々あるが、今回は急な階段の斜度として、25-30度位としておく。ちなみに、京都駅北口のエスカレータで実測したところ、25,6度であった。
それでは、スカートの丈が32cmで階段の角度が30度である場合の計算をしてみる。女性の股下は仮に70cmであるとしておく。おそらく、身長160cm位であれば、この程度であろう。
それでは、ミニスカートの丈が32cm、30cmの時の「下着防御ライン」を計算したものを示す。
 |  |
緑、すなわち、ミニスカートの丈が32cmの時は「下着防御ライン」は階段とほぼ平行である。それに対して、丈が30cmの時の「下着防御ライン」は、ミニスカートを履いた女性から離れるほど階段よりも上に離れていく。ということは、人間の視点位置が「下着防御ライン」を越えるということである。すなわち、下着が見られてしまうということだ。
階段と「下着防御ライン」の差、すなわち、人の目の高さがこの程度ならミニスカートの下の下着を見ることができる、というものを示してみる。
 |
32cmの丈の場合、10m(1000cm)離れても、目の高さが150以下の人しか「下着防御ライン」を突破できない。すなわち、女性は事実上「下着を見られる恐れがない」といって良いだろう。もちろん、20mとか離れたら別である。しかし、超人的な視力がなければ、そのような条件下で下着を確認することはできないであろう。
それに対して、30cmの丈の場合には6m離れた時点ですでに視点が2mの位置にある人でも「下着防御ライン」を突破できてしまう。これでは、「全ての人に下着を見られてしまう」ということになる。
もし、女性の身長が20cm程度高く、180cm程度であったら、どうなるだろうか。おそらく、股下長さは10cm程度長くなる。すると、上の図(階段と「下着防御ライン」の差)の緑、赤ラインは10cm程度高くなる。それでも、緑の32cmスカートの「下着防御ライン」はやはり安全圏といえるだろう。
また同様に、厚底サンダル・ブーツなどを履いた場合には股下長さが20cm弱高くなると考えられる。この影響を考えると、長さとしては身長の影響よりも大きいわけである。それは、身長の1/2が股下長さの増加に繋がるのに対し、厚底靴の長さはそのものずばり股下長さの増加に繋がるからである。しかし、それでもやはり緑の32cmの「下着防御ライン」は安全圏である。
すなわち、32cmと30cmのスカートの丈の長さの間には、「下着が見える・見えない」に関する分水嶺が確かに存在するのだ。先の、
「30cmだと下着が見えちゃうしぃ。」という発言は理論的に裏付けられたのである。
それでは、次に階段の角度が25度である場合の計算をしてみる。
 |
緑の線、すなわちスカートの丈が32cmの場合の「下着防御ライン」が階段にどんどんすり寄っているのがわかると思う。すなわち、「下着防御ライン」はより強固なモノとなっているのである。階段と「下着防御ライン」が女性から離れるほど近づくのである。次に、階段と「下着防御ライン」の差を見てみよう。
 |
緑線、すなわちスカートの丈が32cmの場合に注目する。 女性から、離れても、近づいても、何人たりとも、下着を見ることはできないのだ。下着がシュバルツシルト半径の中に隠されるといっても良い。女性の安全を確保する「完全安全条件」を満たす「下着防御ライン」が完成されているのだ。
これは階段と「下着防御ライン」が平行である条件を境として、そのような条件が達成される。その条件よりより「下着防御ライン」が強固になると、誰も「下着防御ライン」を突破することはできない。すなわち、「完全安全条件」が達成されるのである。
この絶対に下着を防御可能(「完全安全条件」)な「完全安全条件」とは、階段と「下着防御ライン」が平行である条件であるから、ミニスカートの丈(xcm)をパラメータとして、
Tan[階段の角度] = (x-25)/14で計算することができる。ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である。もちろん、極端な安産体型の場合には、その14という値を適当に補正する必要がある。
さて、この条件には女性の身長(股下長さ)は関係しないところが面白い。もちろん、厚底サンダルなどを履いても同じである。もちろん、若干の影響はあるが、あまり影響はない。
さて、今回の「ミニスカートの幾何学」の考察により、判明した結果をまとめてみよう。
ミニスカート内部の下着が「見える・見えない」には
- ミニスカートの丈が30cmと32cmの間に、分水嶺が確かに存在する
- 絶対に下着を防御可能(「完全安全条件」)なミニスカートの丈(x cm)とは、Tan[階段の角度]= (x-25)/14 により決定される
- ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である
- 極端な安産体型の場合には、その14という値を適当に補正する必要がある
- 一方、ミニスカートを履いている人の身長はほとんど影響を及ぼさない
- 厚底サンダルの方が身長よりは影響を及ぼすが、それでもほとんど影響はない
ミニスカートを身につける女性の経験に基づく、「30cmだと下着が見えちゃうしぃ。」理論はなかなか正しいことがわかる。経験というものを軽んじてはいけない、という良い?例かもしれない。結果の伴わない理論に価値はない、ということだろうか。
それにしても、厚底ブーツにミニスカートを履いた女性達は、ロールプレイングゲームの主人公達のようだ。色々なアイテムを手に入れ、冒険を続けている主人公達のようである。ほんの少しだけ、うらやましいような気もする。
さて、こういう話題を書くと少し不安がある。もちろん、私もミニスカートを見ると、妙に心が落ち着かないのも確かに事実ではある。しかし、だからといってことさらに興味津々というわけでもない、と思う。多分。ということで、「できるかな?」の女性読者の数が減少しないことを、ただ祈るのみである。
2000-02-06[n年前へ]
■パノラマ写真と画像処理 Pt.1 
パノラマ写真を実感する
「パノラマ」という言葉は何故か大正ロマンを感じさせる。かつて、流行ったパノラマ館や江戸川乱歩の「パノラマ島奇譚」という言葉がそういったものを連想させるのだろう。私も自分で写真の現像・焼き付けをしていた頃は、フィルム一本まるまる使ってベタ焼きでパノラマ写真を撮るのが好きだった。
そういう癖は持ち歩くカメラが「写るんです」と「デジカメ」へ変化した今でも変わらない。例えば、
の時に撮ったこの写真もそうである。 |
そしてまた、次に示す写真もそうだ。これは1999年夏頃の早朝に箱根の湖尻で撮影したものである。360度のパノラマを撮影したものだ。
 |
観光に行った先で撮影したと思われるかもしれないが、残念ながら違う。出勤途中に撮影したものである。豊かな自然がありすぎて、涙が出そうである。
パノラマ写真としては、こういう景色を撮ったものも良いが、人が写っているものも良い。私の勤務先がこの大自然の中に移転してくる前、都会の中にあった頃に居室で撮ったパノラマ写真などはとても面白い。窓の向こうにはビルが見えたり、周りに写っている人ですでに退職した人が何人もいたりして、涙無しには見られない。
もちろん、こういった写真はパノラマ写真で楽しむのも良いが、もっと実感できるものに加工しても楽しい。私がかつて都会の居室で撮影したものは、当時はAppleのQuicktimeVRのムービーファイルに変換して遊んでいた。今はもうない居室の中をグリグリ動かすのはホロ哀しいものがあり、とても味わい深かった。
ところで、WEB上でそういうパノラマのVRファイルを見せるにはどうしたら良いだろうか?もちろん、AppleのQuicktimeVRを用いれば良いわけではあるが、プラグインが必要である。私はQuicktimeは好きであるが、ブラウザーのQuicktimeのプラグインは嫌いである。WEBを眺めているときに、「Quicktimeのアップグレードはいかがでしょう?」というダイアログが出ると、少しムッとしてしまう。そこで、Javaを使うことにした。いや、もちろんJavaをサポートしていないブラウザーもたくさんあるが、こちらの方がまだ好きなのである。
そのようなパノラマのVRを実現するJavaアプレットには、例えば
- Panoramania
- http://www.lamatek.com/lamasoft/Panoramic/test.html
- Javaアプレット(パノラマver1.1)
- http://village.infoweb.ne.jp/~fwbc6098/java/panorama/panorama.htm
- TheVRApplet1.0
- http://www.physik.uni-greifswald.de/~jonas/VRApplet/VRApplet.html
- how toinsert the panorama show (java applet) inside your home page ?
- http://persoweb.francenet.fr/~carl/brique/exapano1.htm
さて、ここまでは単なる前振りである。本題は、実はこれから始まる。先日このようなメールを頂いた。
私はWindowsを使っているのですが、AppleのQuicktimeVRに興味があって、QuicktimeVRのパノラマ・ムービーを作っています。しかし、素材となる画像の作成に四苦八苦しております。ご承知の通り、
- ライカ版カメラに24ミリ広角レンズをつけて、
- 三脚にパノラマヘッドをつけて、ぐるりと周囲を12枚撮りして、
- 現像、プリントし、
- スキャニングして、ステッチャソフトでレンダリングし、
- それをMacintosh上でMake-QTVR-Panoramaにドロップして、
- 8ミリビデオに広角レンズを付け、
- 90度横倒しにして、10秒程度で1回転するようにステッピングモーターで駆動するパノラマヘッド(自作)に乗せ、
- 高速シャッター撮影し、
- マックのAV機能で円周12枚の静止画を取り出
- し、
- 8ミリビデオを横倒しにして、
- モーター回転するヘッドでぐるりと360度撮影し、
- その撮影した動画ファイルの、各フレームから走査線にして数本分を抽出し(インターレースで256本のうちセンター128本目の前後数本の走査線分)、
- それを貯めて1枚のjpgファイルにする、
- そのJPEG画像をMakeQTVRPanoramaの入力にして、パノラマムービーを作る、
その場合には、スリットスキャンカメラを入手し、それをカラープリントする設備を準備すればいいのでしょうけど、高価です。
そこで、
長々と分かりにくいことを書きましたが、要は、「マックで動く電子スリットスキャンソフト」をなんとか作っていただけないでしょうか?もし、そのようなソフトがあれば、
まずは、答えを先に書いてしまおう。私が作らなくても、
- NIH-Image (MacOS)
- ScionImagePC (Windows)
- 複数画像(動画)からの走査線抽出
ScionImagePCの動作画面を以下に示す。NIH-Imageとほぼ同じである。
 |
これらのソフトのStack-Slice機能を用いれば「複数画像(動画)からの走査線抽出」ができる。その使用例と、その面白い座標軸変換について考えてみたい。しかし、このページは少々重くなってきた。まして、走査線の抽出の話は使用画像が多くならざるをえない。そこで、次回、詳しく使用例を紹介することにする。よく、次回といったまま数ヶ月経つことがあるが、今回は大丈夫である。少なくとも数日後には登場することと思う(多分)。
あれっ、ここまで書いてからinfoseekで検索すると、
- パノラマ写真のひっみっつっ!
- http://www.imagica.com/nomad/sig98/hitachi/
2000-06-16[n年前へ]
■ヘルメットの色空間分布 
学生運動の色空間とグラフ配置
さて、私は「迷信の押し付け」は大嫌いである。もちろん、その人の中で信じている分には結構で、それも文化の一つだとは思う。しかし、それを私にまで押し付けられるととたんにムッとしてしまう。そんな私ではあるが、「占い」はそう嫌いでもなかったりするのが面白いところだ。いや、むろん「占い」を信じているわけでは毛頭無くて、「遊び」として好きなのである。
何しろ、占いというのは「根拠無し」に「決めつける」ことが出来る素晴らしいものである。何の前振りもなしに
「君はお菓子の食べすぎでデブになる。」と言うと、普通であれば張り倒されることだろう。しかし、それを
「君の前世は象だった。だから、君は太る運命だ。」と言えば、どうなるだろうか。悪いのは「前世」や「運命」であって、「口の悪い私」ではないのである。それどころか、
「えぇ〜、なになにその占い〜。教えて、教えて〜」という好意的な反応すら予想される(あくまで予想だけ)のである。これを便利と言わずして、何と言おう。
しかも、占いの特徴の一つは後付けの結論・理由付けが可能、というところにある。その結果、「占い」というものは現実にとても近くなり、さらに「本当らしさ」がアップする。そういうわけで、私は大好きなのである。
例えば、私の職場の私の机の端には、名前、生年月日、アンケート式etc.といったありとあらゆるタイプの占いを職場の人がやった結果がファイルされている。そして、恐ろしいことにそれらの紙には、それを読んだ人の書き込みがあるのである。例えば、私の性格占いの結果をプリントアウトした紙を見てみると、「もう少しイイ子になる必要があります。」という文章の下に赤線が引っ張ってある。この赤線を書き込んだのは誰だか知らないが、実に失礼な輩である。また、「思ったことをすぐ口に出す傾向があります。」という部分は二重線が引っ張られており、これなども世の中には訳のわからないことをする人間がいる良い一例である。そのくせ、「とても心優しいひとです。」という部分は赤線で消されたりしているのが、私としては理解に苦しむ部分でもある。きっと、この書き込みをした輩は「心優しい」という意味を知らないのであろう。
そういうわけで、こういった人々による書き込み・添削のされた占いの結果、すなわち、後付けの結論・理由付けのされた占いの結果と言うのは実に恐るべき迫真性を持つのである。そして、同時に笑うことができる(本人は別にして)、という素晴らしいものなのである。
ところで、私は「色」が大好きである。もう、何回も「色」に関する話題をしているのだから、そんなことは言うまでもないかもしれない。そこで、「色」と「占い」との関連で言うと、一時期「色占い」というものが流行っていた。「XX色で連想する人は誰?」という質問をして、この色で連想された人はあなたにとって恋人、とか、この色は友達、とか占うのである。
私もこの「色占い」が流行ったときにやった記憶があるのだが、これが全く役に立たなかった。役に立たなかった理由の一つに
- 私の周りの人は服なんて着替えない。
- だから、いつも同じ服を着ている。
- その服のイメージ = その人のイメージになる。
そのために、当時の学生の典型的?な姿を下に示してみる。いや、正確に言えば典型的ではなくて、単に目立っていた学生と言うほうが正しいかもしれないが、その姿を示してみたい。
 |
この絵を見るとわかるように、頭の部分を覆うヘルメットというのは何より目立つのである。この人達が身に付けている服装というものは、そんなにカラフルなものではない。いや、ハッキリ言えば、特徴のない色ばかりである。そりゃそうだ、個性的で目立つ色の服なんか着ていたら、個人的に目をつけられてしまう。
しかし、それに対してヘルメットの部分は実にカラフルである。セクトごとに個性ある色分けがされている。人目見ればわかるような色使いがされている。それは、チームスポーツのユニフォームと同じである。敵か味方か一目で見分けがつかないと、困ってしまうわけである。
そして、そのヘルメットの色の印象が強いがために、
その人達の印象 = その色というような状況すら生まれるのである。だから、先の「色占い」のような質問はそのような場においては、何の意味も持たないのである。それは単なるセクト分け問題と化してしまうのである。とたんに、生臭い問題になってしまうのだ。
ところで、さまざまな場所に位置する各セクトが、どのような「色」の住み分けをしているかは、非常に気になるところである。「色」に常日頃こだわってきた「できるかな?」であるから、各セクトのヘルメットの色空間における空間分布を見てみることにしたい、と思う。
そこで、マルチメディア共産趣味者連合 中央委員会の
- ヘルメットで見るセクト( http://marukyo.cosm.co.jp/MET/index.html )
 |
こうしてみると、ヘルメットによる色表現を考えてみると結構広い「色空間分布」になっているようである。カラー画像をヘルメット画像に色分解する、ヘルメットディザなんていうのも実現できるかもしれない。
しかし、これだけではつまらないので、
- 学生活動家組織の変遷 (http://marukyo.cosm.co.jp/KEIZU/gakusei-keizu.html )
そして、グラフ配置の結果の一例を色空間に重ねてみたものを次に示す。
 |
この画像と先程の「ヘルメットの色空間分布」を比較してもらうと、結構似ているのが面白いところだと思う。もちろん、似たような配置になったものを使用したわけではあるが、それにしても面白いと思うのだが、どうだろうか?
私が大学に入学した当時は、セクト間の陣地争いが盛んだった。といっても、私のいた学校がガラパゴス諸島のように(その手の部分では)化石的な学校だったからで、決して古い昔の話ではない。授業をやっている横の廊下で、内ゲバで殺される人がいたり、朝のキャンパスで血みどろの戦いが行われていたりした。実際のところ、それは私にとって結構衝撃的な出来事だった。少なくとも、そのせいで、あの手の陣地争いを大嫌いになったことは確かだ。とりあえず、現実空間ではともかくこの色空間においては、そんな陣地争いがないのが良いところだ。
さて、今回はタイトルをゲバ字(トロ字)っぽくしてみた。ゲバ字(トロ字)というのは、チラシや立て看などでよく使われた(る?)文字のことである。だから、別に「こういう形」というものがあるわけではない。とりあえず、それっぽくしてみたわけであるが、どうも本WEBにはこういうフォントは似合わないようである。うーむ、失敗である。