2001-06-21[n年前へ]
■二十一世紀の「ミニスカートの幾何学」 
可愛いAIBOはちょっぴりエッチ
「面白い記事がありましたが、読みましたか?ふふっ(笑)。」というメールが先日私に届いた。さてさて、一体どんな記事だろう?うむむ…?と見に行ってみると、それはZDNNのこんな記事だった。
- 「しつけ」られたAIBO——無線遠隔操作ソフトに,盗撮防止機能
- ( http://www.zdnet.co.jp/news/0106/08/aibo.html?0b06012410 )
しかし、しかし、である。これだけでは、先のメールの書き主が私にわざわざこのニュースを知らせてくれる理由がわけ判らないではないか。私はお茶ノ水博士のようなロボット博士でもなければ、TVチャンピオン常連のおもちゃオタクでもないのである。ましてや、先のメールの「ふふっ(笑)」は奇奇怪怪としか言いようが無い。もしかしたら、これは新手のAIBOの売り込みだろうか?あのSONYもついにSPAMを出すようになったか、あのSONYがなぁ、と思いつつ記事を読み進んでいくと、記事の終わり近くになってやっと疑問は氷解したのである。その部分を少し引用してみると、
今回,遠隔撮影を可能にするAIBO Navigator開発にあたって,ソニー社内でも盗撮問題が再浮上。AIBOを担当するエンターテインメントロボットカンパニー内に「倫理委員会」を設置するなど,盗撮問題に対して真面目に取り組んだという。ということだそうだ。なるほど、これはまさにである。理系学生の憧れナンバー1といえばソニーであるが、そのソニーの「真心」とも言うべきソニーの「倫理委員会」と私は同じような「研究」をしていたわけである。「女性のためのミニスカート理論の構築を目指していた」ミニスカートの幾何学はまさに「真心・倫理」を具現化した研究と言っても良いくらいであるが、やはり判る人には判るのである。先のメールの主は私に「あなたのレポートはまさに日本の倫理のために役立っているのですよ」と教えて下さっているに違いないのである。もっとも、残念なことに私はソニーの倫理委員会と違って「短いといわれているミニスカートの丈の長さを実際に定規で測って調べたり」する機会には恵まれなかったのである。
「AIBOのアタマが,ある角度以上に上を向くと,見てはいけないものが見えてしまう」(ソニー)ということで、倫理委員会では、まず盗撮される側のデータを収集。女性の平均身長の調査から始まり、短いといわれているミニスカートの丈の長さを実際に定規で測って調べ、AIBOの頭部カメラがどの角度までなら大丈夫かをさまざまな角度から調査。その結果、可動角度を最大20度とし、首の位置が20度以上動くようなモーションをしなくてはいけないときは、動画が止まる機構までも装備した
が、そんなことはさておき、「角度で20度までなら、見てはいけないものが見えない」というのは本当だろうか?それは、ミニスカートの幾何学で調べるとどういうことになるのだろうか?というわけで、このナゾについて少し考えてみたい、と思うのである。
というわけで、まずは「ミニスカートの幾何学」の復習をしよう。ミニスカートの内側の下着が見えるか、見えないかを考えるには次のような図を考えると判りやすい。ここでは女性の真下の地点を原点にとり、水平方向にX軸をとり、鉛直上向きにY軸をとっている。
 |
スカートの内側の「見てはいけないもの」が見えてしまうのは、上の図で緑の線よりも下側に入って、その緑の線より上を見上げた場合である。そして、ここでその緑の線は
- 女性の下着の一番下の部分の位置
- ミニスカートの一番端の下の位置
それでは、その「限界角度」を調べるために、とっても簡単「ミニスカートの幾何学」を活用しよう。まずは、例えば女性のヒップ周りが88cmとしてみた場合に、スカート中央から端までの長さ(rcm)は、女性のヒップを円と近似すると、
2πr = 88cmであるから、スカート中央から端までの長さ(r cm)は
r = 14cmとなる。すると、図を見ればわかるように、緑の線 -> 「下着防衛ライン」はスカートの丈を未知数として、
y = - ((スカートの丈 - 25)/14) x + 股下長さという式で表すことができるわけだ。ここで、「AIBOがそれ以上上を向くと見てはいけないものが見えてしまう」という緑の線の角度は
ArcTan[ (スカートの丈 - 25)/14 ] / (2 π)*360で表されるから、それを計算してみて、「スカートの丈」に対する「見てはいけないものが見えてしまう」限界角度を計算してみると、その結果は次のグラフのようになる。
 |
このグラフを見れば判るように、女性のスカートが長くなれば長くなるほど、「見てはいけないものが見えてしまう」限界角度は大きくなる。当り前である。長いスカートの中を覗こうとしたら、AIBOはそのスカートの中へ入り込んで、かなりの上を見上げなければならない。もちろん、スカートの丈が短くなればなるほど、スカートの中身は覗きやすくなる。そうすると、AIBOがそれほど上を見上げなくても、「見えてはいけないもの」が見えるようになってしまうのである。
さて、前回の「ミニスカートの幾何学」では女性達が履くスカートは短くても32cmまでであって、その長さであれば角度が30°ほどにもなる急な階段でも女性のスカートの中の「見えてはいけないもの」は見えることが無い、ということを明らかにした。というわけで、それを知ってか知らずか女性達の履くスカートは短くても32cmまでなのである。だとすれば、その32cmに対応する限界角度は「見てはいけないものが見えるための必要角度」ということになるわけである。
すると、このグラフを見れば一目瞭然、スカートの下限「見てはいけないものが見えてしまう」限界角度は20数度よりも大きいことが判るのだ。ということは、先の記事の通りに、AIBOの首の上限角度を20度にしておけば、もうどうやってもAIBOはスカートの中身を覗くことができなくて、AIBOが盗撮者の手先となってしまう危険は防ぐことができるのである。それより上を眺めれば、見たことのない映像が見ることができるハズなのではあるが、ロボット三原則に基づいて(大ウソ)、AIBOの首はそれより上には上がらないように設計されているわけである。
というわけで、こんな風にソニーの「倫理委員会」がうらやましいばかりの数々の実験を重ねて調べたことも、このミニスカートの幾何学から導き出すことができるのだ。あぁ、なんて社会の役に立つ研究なのだろう。こんな女性のため、社会正義のための幾何学がこの他にあるのだろうか…。しかし、そんな社会正義のための研究だったハズなのに、この「ミニスカートの幾何学」をきっかけにしてhirax.netが色モノサイト扱いされ、さらには有害サイト扱いされるようになるとは… 思いもしなかったなぁ… ふっ… (涙)…。
2001-07-07[n年前へ]
■七夕の夜に願うこと 
ベガとアルタイルと一通のメール
今日は七月七日、七夕だ。その夜、天の川の両岸で光る織女星と彦星が一年に一度だけ逢う。織女星は琴座(Lyra)のα星ベガ(Vega)で、彦星は鷲座(Aquila)のα星アルタイル(Altair)である。
 |
ベガは地球から25光年離れた場所にあり、その明るさは0等のとても明るい星だ。もう一方のアルタイルは地球から17光年離れている。そして、ベガとアルタイルの間の距離は15光年離れている。それを15光年「も」離れていると思うか、15光年「しか」離れていないと思うか、それは人によって違うだろう。15光年「も」離れていると思う人は、ベガとアルタイルの間で言葉を交わしても、その言葉が往復するのに15×2= 30年もかかる、と考える。そして、15光年「しか」離れていないと思う人は、たった30年で言葉が通い合う、と考えることだろう。人それぞれだ。
誰かと待ち合わせている時、遅れた相手を例え5分間でも待つのも耐えられない人もいる。そして、1時間も相手を待つことが苦にならない人もいる。もちろん、それは誰を待っているかとかどんな状況かとかにもよるところが大きいだろうけれど、とにかく人それぞれの時間感覚があるわけだ。
人にもそれぞれの時間感覚があるように、生物にはその生物それぞれの固有の時間間隔がある。しかも、それだけでなくて、
で考えたように、生物に限らずあらゆる系でその系固有の時間感覚があることだろう。だったら、ベガとアルタイルの間で信号が伝わりあう30年という時間はベガとアルタイル自身の時間感覚からすると、それは長いのだろうか、それとも短いのだろうか。一体、どんなものなのだろう?まずは、星の寿命を普通に考えてみれば、ベガもアルタイルも主系列星で、それぞれの重さから寿命を計算することができる。ベガとアルタイルと体重は本当はちょっと違っていて、女性のベガの方が実はちょっと太っているのだけど、あまり女性のベガの重さを正確に言ってしまうと、当然機嫌を悪くするだろう。だから、ちょっと大雑把に言うとベガもアルタイルも大体太陽の3倍位である。それを使って寿命を計算してみると、彼らの寿命は100億年位になる。人間の寿命の1億倍である。逆に言えば、ベガとアルタイルの時間感覚は人間の一億倍ゆっくりだということになる。それだけ、人間に比べて二人は気が長〜いのである。
ところで、寺田寅彦・ロゲルギストなどが考えたように「系の寿命はそのものの大きさに比例し、それに応じた固有の時間感覚を持つ」として、ベガとアルタイルの時間感覚を適当に考えてみると、これが実はちょっと面白い。ベガとアルタイルの大きさはそれぞれ太陽の3倍、1.7倍なのだが、その程度の大きさの生物だと、その寿命は大体20億年位だという計算結果になる。これらの数字のオーダーからすれば、もうさっきの100億年という数字と全く同じだと言っても良いくらいである。まぁ、いずれにせよベガとアルタイルの時間感覚は人間の1億倍近く「気長」ということに変わりはない。
すると、ベガとアルタイルの間の30光年- 信号が往復するのに30年かかかる-という距離は、彼ら二人にとってはどの程度の時間だろうか?人間より一億倍気が長いベガとアルタイルにとって、人間にとっての15年はどの程度の時間だろうか? 試しに計算してみると、
30年×365日×24時間×60分×60秒 / 1億 = 9.5秒で、10秒弱ということになる。10秒というと、電話で話すというには無理があるかもしれないけれど、e-mailのやりとりよりにかかる時間よりはずっと短い。月に着陸しているアポロ宇宙船と地球との会話だって実は3秒近くかかる。ベガとアルタイルの間の「10秒(ベガ・アルタイル体感時間)」というのは、電話をしたり実際にベガとアルタイルが会って話をしたりするのには負けるだろうけれど、それでもメールをやりとりするのに比べたら、ずっと近い距離(時間)なのである。ベガとアルタイルはとても「近い」のだ。天の川の両側に離れていはいるけれど、やっぱり「近い」のである。
そういえばベガというと、地球の歳差運動により、一万二千年後にはベガは地球から見て天の真北に位置することになる。つまり、一万二千年後には織女星ベガは北の空の中央で輝いて、その時彦星アルタイルは織女星ベガの周りを回り続けることになる。ずっと先のことに思えるかもしれないけれど、一万二千年後なんてベガとアルタイルの時間で言えばたったの一時間後である。一時間後(ベガ・アルタイル時間)には、アルタイルはベガの周りをクルクルと回っていることになる。なんだか、そんなベガとアルタイルがほほえましく思えてしまうのは私だけだろうか。何か、そんなベガとアルタイルをちょっとからかってみたくなるくらいに思えてしまう。
ところで、そんな風にベガとアルタイルをからかうためではないけれど、アルタイルにかつて地球からメールが出されたことがある。スタンフォードの46mのパラボラアンテナからアルタイルに向けて、13枚の画像が送り出された。その13枚の画像は本当に子供の落書きのような過去の生物の画や人間の姿が描かれていた。そんな子供心いっぱいの画像もあるかと思えば、差出人(平林・森本)が二人とも飲むのが大好きだったので、メッセージの最後はアルコール分子の組成式で締めくくられていた。本当に、ちょっと間違えるとベガとアルタイルをからかうヨッパライになってしまいそうである。
 (「星と生き物たちの地球」 平林久、黒谷明美から) |
1983年に送ったメッセージはもう昨年にはアルタイルに届いているはずだ。アルタイルからメッセージが帰ってくるとすれば、それは2016年になる。あと15年先だ。15年なんて、アルタイルからすれば5秒弱(彼にとっては)であっという間の時間だし、私達人間にとってもやっぱり15年なんてあっという間の時間に違いない。もちろん、本当のところアルタイルからの返事が帰ってくるわけはないのだけれど、だけどそれでも「 はじめまして、アルタイルです…」なんてメールが帰ってくるときのことを想像するのもとても面白いことに違いない。もしかしたら、2000年にアルタイルから送り返されたメールの返事が宇宙空間を秒速30万kmで走ってくる途中かもしれない、と酔っ払った頭で夢想してみるのも楽しいことだろう。
ところで、本来の七夕は旧暦の七月七日だから、今年の本当の七夕は八月二十五日ということになる。今夜七月七日を過ぎてしまったからといって、七夕が終わってしまうわけではない。これから続く夏の空を眺めつつ、ビールでも飲みながら、天の川とベガとアルタイルのことや、酔っぱらい達が送ったそんなメールのことを思い浮かべてみるのも、きっと風流で気持ち良いはずだ。星空の綺麗な高原で、あるいは星なんて見えないビル屋上のビアガーデンで。
2001-07-25[n年前へ]
■遠い空のはて? 
地平線の向こうに手を伸ばせ
先日、富士山の五合目へ行った。と一言で言っても、富士山の五合目にも色々ある。何しろ上り口が、第一人気の「吉田口・河口湖口」、下りの「砂走り」で有名な「御殿場口」「須走口」、そして測候所の白ドームを目指し最短距離一直線の「富士宮口」と四種類もあるのだ。その色々ある五合目の中で、先日私が行ったのは富士宮口の五合目というところだ。富士山の太平洋側から富士山頂に向かう登山口の標高2400m地点ということになる。もしかしたら、表富士五合目と言う言い方のほうが有名なのかもしれない。
その表富士五合目から下を眺めると、ずいぶんと遠くまで見えることに本当に心からビックリした。雲が下のほうに広がっていて、そしてその向こうに海や山や地平線が見える。そして、気のせいか地平線がとても丸いような気がする。その五合目までは車で簡単に来ることができたのだけれど、さすが標高2400mは伊達ではなかった…。やっぱり富士山は日本一の山かもしれない…。そして、そんな景色を眺めているうちに、私は色々考えてしまった。
あぁ、下を眺めると遠くまで景色が本当にきれいだ。そういえば、眺めると言えば…これまで、私は急な階段の下から上を眺めたらスカートの内側の下着なんかを覗けるかどうかをジックリ考えてみたりしてきたなぁ。それに、SONYの誇る可愛いらしいAIBOの気持ちになって、やっぱり同じく低いAIBOの視点から上を見上げたらやっぱりスカートの内側が覗けるかどうかを考えてみたりしたなぁ。見上げてばっかりだなぁ、しかも、どれもスカートの内側かぁ…。
そういえば、透け透け水着もマズかったなぁ…。あれ、本当に仕事の話から始まったんだけどなぁ…。誰も信じてくれないし…。あぁ、だけど、やはりそんなことを考えていてはいけなかったんだ…。そんなことをしてたから、画像処理追求サイトを目指したハズだったのに、何時の間にか有害サイト認定されてしまったりしたに違いないんだ…。ついには、「こどもに見せられないページ」保証までされたりするしなぁ…
私は一体何処で間違えてしまったのだろう…? あぁ、それにしても地平線がきれいだ…。地平線が丸い…。 あぁ、地球はやっぱり丸いんだなぁ…。
と、まるで「生きる」で「ブランコに乗りながら人生を振り返る」志村喬のように、我が身を振り返っている内に、ふと「そういえば、地平線って一体どのくらい向こうにあるんだっけ?」と考えはじめてしまった。そもそも、地球が丸いからどうしてもある距離以上は見通すことができなくて、それが地平線なわけだけど、それは一体どのくらい先なのだったのだろうか?
おぼろげな記憶を辿ると、意外に地平線は自分の近くにあって、確かほんの数km先程度だった気がするのだけれど…。さて?あれ? はて… 果て…?
というわけで、地平線までの距離を計算してみた。まずは、そのために下図のように視点の高さYと地球の半径Rをとってやる。
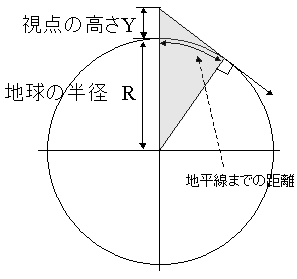 |
「視点位置」と「地球中心」と「地平線」を結んだ三角形(グレーで塗りつぶした部分)がもう簡単なくらいに直角三角形なことに注目して解いてみると、「地平線までの距離」は「視点の高さY」の関数として
というような形になる(計算が合ってれば…)。これに、地球の半径R = 6400kmを代入してやれば、視点の高さYに応じた地平線までの距離が求められるわけだ。
そこで、まずは視点の高さが0〜3m位までの場合をグラフにしてみたのが次の図である。歩き始めて広い世界で暴れだすだろう頃の一才児の身長を緑○、そして、かつてはデカイの代名詞といえばコイツという存在だったアンドレ・ザ・ジャイアントの身長223cmを青○で記入してみた。
青:アンドレ・ザ・ジャイアントの身長 = 223cm  |
このグラフを見ると、一才児の地平線はおよそ3km先にあって、アンドレ・ザ・ジャイアントの地平線は5〜6km先にあることがわかる。もちろん、その間の身長の人達の地平線はその中間、そう4km先くらいにあるわけだ。私たちの地平線はほんの4km先、なんと走ればほんの20分位のところ、歩いても一時間かからない程度の近くに地平線はあるのだった。地平線なんていうと、遥か遠くにあるように思えるけれど、手の届くほんのすぐ先にいるのである。
そして、歩き始めた子供の地平線と巨人アンドレ・ザ・ジャイアントの地平線がたいして変わらない、というところも面白いものだ。あれだけ背が高ければ、さぞかし広い世界を眺めているのだろう、と思ったりするがそういうわけでもないのである。
じゃあ、もう少し高い場所に行くとどうか、ということで1000mまで視点の高さを上げてみたのが次のグラフである。東京タワーの特別展望台の250mを緑○で、あくまで計画中の秋葉原タワーの特別展望台の500mを青○で示してある。 ここまで上がると、250m地点で地平線は60km先になり、500m地点では80km程度先まで見通せることになる。東京駅の位置からの距離で言うと、60kmでは箱根くらい、80kmで三島くらいだろう。
青:計画中の秋葉原タワーの特別展望台 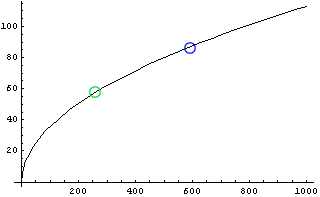 |
調子に乗って、さらに視点を高くしてみよう。先の表富士の五合目2400m地点では200km近く見渡せ、東京駅からの距離で言うと地平線は遠く浜名湖辺りまで離れていく。そして、さらにさらに視点を上昇させ、ジャンボジェット機の巡航高度地上10kmからであれば、なんと350kmほども見渡せるのである。350kmだと東京駅から京都くらいだろうか。東京-京都と言えば、そうちょうど東海道五十三次だ。江戸時代の人達が一月近くもかけて歩いたくらいの彼方まで地平線は後ろへ下がっていくわけだ。地平線は時が流れるにしたがって、遠くに広がっていくのだ。
青:ジャンボジェット機の巡航高度 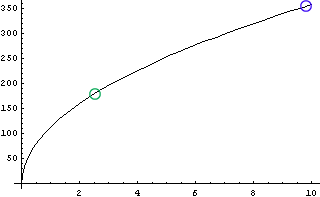 |
そのジャンボジェット機から見える地平線は、かつては一月近くもかけて歩いたくらいの遠く、400kmも遠くなのだから、そこまで行くと地平線が「遥か遠く」に思える。一瞬そう思える、のだけれど実はそんなことはない。ジャンボジェット機の速度からすれば、そんな遥か彼方の地平線だって、やっぱり30分ちょい位のすぐ近くだ。私たちが普通に立っているときの地平線が4〜5kmくらいのすぐ近くにあって、歩いてみればやっぱり30分ちょいで行ける、というのとほとんど同じなのだ。

ジャンボジェット機から眺めた地平線(水平線)
五歳くらいの子供の地平線と、空を飛び回るジャンボジェット機の地平線を時間を距離の単位として比較してみれば実はほとんど同じ遠さだ、というのは何だかとても面白い。大地の果てと天とが接っする地平線はとっても近くにあって、そこまで行くのにかかる時間は小さな子供でも巨大なジャンボジェット機でも同じなのである。
「地平線」なんて言うと、まるで「手が届かないもの」の代名詞みたいに使われたり、あるいは「その先には何があるのかわからないもの」の代名詞に使われたりするけれど、ちょっと行こうとして見れば、片道30分ちょっとでその「地平線」まで辿りつくことができるわけだ。案外、遠くにあると思い込んでいるものも、手を伸ばしてみれば、もしかしたら手が届くものなのかもしれない。しかも、それは地平線まで辿り着く時間が小さな子供でも巨大なジャンボジェット機でも同じだったように、誰でもできたりするものなのかもしれない。
もちろん、かつての「地平線」だった場所まで辿り着いたとしても、新しい「地平線」は視界の向こうに下がって行くわけなのだけれど、そこまでだってやっぱり歩けばほんの30分だ。遠い空の果て、地平線の向こうは、すぐそこだ。
2001-10-12[n年前へ]
■今日見た景色 「手を上げてるこども」 
狭い道で車を走らせていると、道を渡るために手をとてもしっかりと上げている少年が目に入った。小学校の低学年だろう。意志の強そうな目がこっちを見てた。前後の車間距離が狭くて止まることはできなかったけど、意思の強そうな目が印象的だった。何かとても強いものを見たような気がして、止まれなかったことにちょっと後悔した。
2001-10-15[n年前へ]
■瞬間写真の立体写真 
今日、瞬間写真プロジェクトに自分の分を送付したのだけれど、ふとこんなことを考えた。
同じ瞬間に、もし本当にすぐ近くで写真を撮った二人が居たとしたら、その二人の写真を同時に眺めてみれば、それは立体写真に見えるのだろう。もちろん、その立体写真が自然に見えるためには二人は顔を寄せ合うくらいの距離でカメラを覗かなけりゃならないかもしれないけれど、それはそれで面白いかもしれないな、と思ったりしたのだった。