1998-11-20[n年前へ]
■モアレはデバイスに依存するか? 
まず、以下のような2つの同心円画像をつくる。(なお、このような画像を簡単に作るために、Photoshop用のフィルターを作った。詳しくは「Photoshopの同心円フィルターを作る。」を参照して頂きたい。)以下の2つの画像は少し中心位置がずれている。また白く見えるところは255の値を持ち、黒く見えるところは0の値を持っている。(画像自体は512x512であり、表示の際に128x128に変換している。だから、この画像をそのまま保存して頂ければ、512x512のサイズで保存することができる。)
 |
 |
- 黒(0)+黒(0)=0(すなわち黒)
- 白(255)+白(255)=255(すなわち白)
- 黒(0)+白(255)=255(すなわち白)
- 画像1を白黒反転し、画像1'を作る。
- 画像2を白黒反転、画像2'を作る。
- 画像1'と画像2'を加算し、画像3を作成する。
- 画像3を白黒反転し、画像3'を作成する。
 |
それでは、以上の画像変換を小さい画像でまとめて表示してみる。
 |  |  |
ところで、上の3つの画像をそれぞれ平滑化してみる。すると、以下のようになる。
 |  |  |
以下でもう少し詳しく考えてみる。
重ね合わせにおける加算演算
下のような画像A、画像Bを考える。拡大してあるが、画像自体は1x2ピクセルのサイズである。また、白=255、黒=0とすれば、いずれも平均値は128程度である。 |  |
- 黒+黒=黒
- 白+白=白
- 黒+白=黒
 |  |  |
 |  |  |
 |  |  |
これに平均値も示すと以下のようになる。ここでは、LBPなどの紙に出力する際によく使われる、白=0、黒=255という表記をする。
 |  |  |
 |  |  |
 |  |  |
同じ128+128でも、結果は128になるか256になるかの2種類ある。同じもの同士であれば、結果は128であるし、そうでなければ256になる。そのために、平均値が保存されないのである。このように、平均値が保存されない、言い換えれば、加算演算の結果が線形でない場合にはモアレが発生することになる。もしも、マクロに見て「128+128=256」が多い領域があれば、それはモアレの黒い部分であり、そうでない所は比較的明るい部分であるということになる。
ロゲルギストの-モアレが生じる理由は黒さの非線形性による-という言葉はこの「128+128=128、と128+128=256という結果の違いがあり、それがモアレの原因である」ということを示している。
それでは、そのような現象「128+128=128という非線形性」が起きない状態を作ってみる。それには加算の結果である黒がサチらないようにすれば良い。
 |  |  |
 |  |  |
 |  |  |
これでは、いずれの状態でもグレー+グレー=黒、すなわち、64+64=128という風になっている。これは黒がサチっていないからである。すなわち、-モアレが生じる理由である黒さの非線形性さ-がない状態になっている。
それでは、この状態で計算実験Aと同じことをしてみる。それを計算実験Bとする。念のため、計算実験Aをもう一度示す。
 |  |  |
 |  |  |
 |  |  |
| 画像1の黒=0を128にした画像4を平滑化したもの | 画像2の黒=0を128にした画像5を平滑化したもの | 画像4,5を加算したもの |
モアレができていないのがわかるだろうか。これはグレー(128)+グレー(128)=256(もっと黒)で線形な関係が成り立っているからである。平均化された画像で濃度がどこも倍近くになっているのがわかると思う。
モアレのデバイス依存性
LBPではトナーが有る所、すなわち、画像が有る所はほぼ完全に影になる。例え、2枚重ねてもやはり影のままである。しかし、インクジェットならどうだろうか。OHPで使うと、黒といってもLBPに比べて薄い。1枚のOHPの黒よりも、2枚のOHPの黒を重ねた方がかなり黒い。ということは、「黒+黒=もっと黒」と同じである。したがって、OHPを重ね合わせても濃度が保存されている。すなわち、モアレが比較的に出来にくいことになる。ということは、OHPを何で作るかによってモアレの具合が変わることになる。付け加えれば、実際のOHPの場合には透過率を考えなければならない。透過率というものは単なる重ね合わせでない、具体的に言えば、加算演算でなく乗算演算である。それでも、話としては大体は同じことである。
今回はOHPの話に絞ったが、透過原稿でなく反射原稿についても同じである。むしろ、反射原稿の方が乗算演算でなく、加算演算である分、今回の話そのままである。したがって、一般的なモアレについてインク(もしくはそれに相当するもの)の加算演算の具合によって、モアレの発生具合が違うと考えられる。
また、話の単純のために白黒の話に限ったが、カラーのモアレなどについてもほぼ同じであろう。トナーとインク、また、混ざりやすいものと混ざりにくい物の違いなどでも面白い結果が出そうである。TVや液晶のようにほぼ線形の重ね合わせが成り立つであろうものと比較するのも面白そうである。
今回の話を考えている途中で、OHPの重ね合わせと干渉の共通点については、結構奥が深いような気がしてきた。そのため、別の回でもう少し詳しく考えたい。
1999-09-01[n年前へ]
■画像に関する場の理論 
ポイントは画像形成の物理性だ!?
今回は、
夏目漱石は温泉がお好き? - 文章構造を可視化するソフトをつくる- (1999.07.14)
の回と同じく、「可視化情報シンポジウム'99」から話は始まる。まずは、「可視化情報シンポジウム'99」の中の
ウェーブレット変換法と微積分方程式によるカラー画像の圧縮および再現性について
という予稿の冒頭部分を抜き出してみる。「コンピュータグラフィックスを構成する画素データをスカラーポテンシャルあるいはベクトルポテンシャルの1成分とみなし、ベクトルの概念を導入することで古典物理学の集大成である場の理論が適用可能であることを提案している」というフレーズがある。
着目点は面白いし、この文章自体もファンタジーで私のツボに近い。しかしながら、肝心の内容が私の趣向とは少し違った。何しろ「以上により本研究では、古典物理学の場の理論で用いられるラプラシアン演算を用いることで、画像のエッジ抽出が行えることがわかった。」というようなフレーズが出てくるのである。うーん。
私と同様の印象を受けた人も他にいたようで(当然いると思うが)、「エッジ強調・抽出のために画像のラプラシアンをとるのはごく普通に行われていることだと思うのですが、何か新しい事項などあるのでしょうか?」という質問をしていた人もいた。
また、話の後半では、画像圧縮のために、ラプラシアンをかけたデータに積分方程式や有限要素法などを用いて解くことにより、画像圧縮復元をしようと試みていたが、これも精度、圧縮率、計算コストを考えるといま一つであると思う(私としては)。
画像とポテンシャルを結びつけて考えることは多い。例えば、「できるかな?」の中からでも抜き出してみると、
- 分数階微分に基づく画像特性を考えてみたい- 同じ年齢でも大違い - (1999.02.28)
- ゼロックス写真とセンチメンタルな写真 - コピー機による画像表現について考える- (99.06.06)
- コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
現実問題として、実世界において画像形成をを行うには物理学的な現象を介して行う以外にはありえない。「いや、そんなことはない。心理学的に、誰かがオレの脳みそに画像を飛ばしてくる。」というブラックなことを仰る方もいるだろうが、それはちょっと別にしておきたい。
「できるかな?」に登場している画像を形成装置には、
コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
で扱ったコピー機などの電子写真装置や、
宇宙人はどこにいる? - 画像復元を勉強してみたいその1-(1999.01.10)
で扱ったカメラ。望遠鏡などの光学系や、
ヒトは電磁波の振動方向を見ることができるか?- はい。ハイディンガーのブラシをご覧下さい - (1999.02.26)
で扱った液晶ディスプレイなどがある。そのいずれもが、純物理学的な現象を用いた画像形成の装置である。
例えば、プラズマディスプレイなどはプラズマアドレス部分に放電を生じさせて、電荷を液晶背面に付着させて、その電荷により発生する電界によって液晶の配向方向を変化させて、透過率を変化させることにより、画像を形成するのである。
 |
また、逆問題のようであるが電界・電荷分布測定などを目的として液晶のボッケルス効果を用いることも多い。液晶を用いて得られる画像から、電界分布や電荷分布を計測するわけである。これなども画像と場の理論が直に結びついている一例である。
参考に、SHARPのプラズマアドレスディスプレイを示しておく。
 |
また、電子写真装置などは感光体表面に電荷分布を形成し、その電位像をトナーという電荷粒子で可視化するのであるから、電磁場を用いて画像形成をしているわけである。だから、場の理論を持ちこむのは至極当然であり、有用性も非常に高いだろう。そういった視点で考察してみたのが、
である。 同様に、画像圧縮に関しても、画像形成の物理性に着目することで実現できる場合も多いと思うのであるが、それは次回にしておく。
2000-03-19[n年前へ]
■一家に一台、分光器 
ハサミとテープで「できるかな?」
いきなりであるが、分光器を作りたい。光を波長別に分ける機器である「分光器」である。とある実験をするために、分光器が必要なのである。その「とある実験」の影には、大きな野望があるのだが、まだ明らかにする訳にはいかない。とりあえず、色の話題を考えるときに分光器があると便利だから、という理由にしておきたい。
どうやって分光器を作るか考えてみる。普通であれば、グレーティング(回折格子)やプリズムといったものを使うことになるだろう。家の中を探してみれば、プリズムなどもあるはずなのだが、WEBで情報を探してみると面白い情報があった。
- CDを利用した分光器の製作
- ( http://www.sunfield.ne.jp/~oshima/omosiro/spec.html )
- 遮光フィルムを用いた分光器の製作(その1)
- ( http://www.asahi-net.or.jp/~DJ9K-SMZ/goods/spectre/spectre.html )
次に示すのが、HIRAX一型分光器である。ハンディ・超軽量の優れものだ。テープとハサミと去年のカレンダーを駆使し、フリーハンドで作成した、製作時間20分の大作である。どうも私の仕事はテープとハサミを駆使することが多い。それは、ハードでもソフトでも、どちらでも同じことである。出来の悪いノッポさんである。
 |
左下がスリット部になっている。中央上の折れ曲がっている部分にグレーティングが配置している。次の写真を見るとグレーティングがあるのが判ると思う。HIRAX一型分光器の内部は散乱光を防止するために、黒く塗ってある。しかし、下の写真を見れば判るように、グレーティングの周りの片側は塗り忘れてしまった。まるで、「耳なし保一」である。
 |
こちらの開口部から目で覗くなり、デジカメで撮影するなりするのだ。そうすれば、スペクトルが確認できる、というわけである。
例を示してみたい。グレーティングが曲がっているせいで、スペクトルが歪んでいるし、スリットが結構太いし、サイズのせいもあってスペクトルの分解能はそれほど高くない。しかし、結構きれいな映像を得ることができる。まずは、太陽光のスペクトルを見てみる。
 |
これはデジカメで撮影したものである。スリットが太いので確認しづらいのだが、太陽光のフラウンホーファー線(FraunhoferLine)の一つHβ吸収線が486nm(ここでは水色の中央部)辺りに見えるような気がしないだろうか? いずれ、スリット幅を小さくして、もう少し精度の高い実験をしてみる予定である。
さて、次の例は「自宅の蛍光灯のスペクトル」である。
 |
- 黄色、橙色 579、577nm
- 黄緑色 546 nm
- 水色 436 nm
- 紫色 408、405 nm
 |
目で覗いたり、デジカメで撮影したりするのも面倒なので、可視・赤外領域に感度を持つCCDボードを秋月で買ってきた。次回、このCCDボードを取り付けて見る予定だ。そして、定量化をしてみたいのである。そして、ある野望のためにせっせと実験を続けていく予定である。
2000-03-26[n年前へ]
■透け透け水着の物理学 入門編 
透過率の波長依存を探れ
少し前のことだった。舞台は妙高高原の露天風呂である。同じ職場の人とある話をしていた。話題は仕事に関する話で、主な話題は色々な物質の光の透過率や吸収の話だった。ずいぶん長いこと、そういった話題をしていた。
しかし、ふと気づくとなにかがおかしい。会話中に出てくる言葉が変なのである。さっきまで話していた「吸収波長」とか、「感度」とかいう言葉は依然として出てくるのだが、それに加えて変な言葉がどうも出ている。「透け透け水着」とか「丸見え」とか「ナイトショット」といった類の言葉である。これは一体どうしたことだ?これは非常にマズイ。
私たちがいるのは露天風呂である。私たちの数m横の壁の向こうは女性用の露天風呂だ。そこで、私たちは「透け透け水着」と「丸見え撮影」の話題をしているのである。非常に危険なシチュエーションである。逆に、隣の女性用露天風呂に入浴している人がいたならば、とてもイヤなシチュエーションである。隣が「変態さんいらっしゃい」状態だと思ってしまうだろう。
もちろん、心ある人が聞けば、私達が極めて誠実に「透け透け水着」と「丸見え撮影」の「科学」について論じているのはわかるはずだ。ましてや、私という人間を知っていたならば、なおさらである。
しかし、周りはもちろん私達の知り合いではないわけで、誤解されても何らおかしくない。いや、誤解されないのが不自然な位である。
もちろん、私は見えないものを可視化するのが大好きであるし、「32cmの攻防戦」について論じたこともあるが、誤解はしないで欲しい、とあの時周りにいた人達にひとこと言っておきたい。
さて、その時に話していたのは、ビデオカメラで水着が透けて見える話についてであった。あの有名なSONYの「ナイトショット」機能付きのHandyCamのことである。そのカメラでどうして水着が透けて見えるのかについて論じていたのである。その見える理由を聞かれた私は「透け透け水着は赤外線の透過率が高いから、と言われていますね。」と答えた。
例えば、「水着、透ける、ビデオ」で検索すれば、そういう解説が数多くある。それに、私は赤外線フィルムを使って風景撮影をするのが好きだったので、いくらか知識もある。しかし、それはあくまでも知識である。実際に水着の赤外線の透過率を調べたことがあるわけでもないし、可視光との差を比較したことがあるわけでもない。それはあくまで知識だけ、である。実証の伴わない知識というのは今ひとつ好きではない(いや、盗撮を実証するわけじゃないけど)。
そこで、今回は「水着が透ける理由」を実証してみたい、と思うのである。 透ける理由として、よく言われている
- 水着の色や生地によって波長毎の光の透過率が異なる
- 水着によっては、赤外光は屈折・散乱しにくく、透過率も可視光に比べて高いものがある
- 簡単に言えば、その水着は赤外光は透過しやすい、ということである
- ということは、赤外光で撮影をする限りにおいて、その水着は半透明であるようなものである
- また、可視光の影響を防ぐため、可視光をカットするフィルターを用いて、赤外光のみで撮影をする
- すると、なんと水着が透けて見える
さて、先ほどの「透け透け水着は赤外線の透過率が高いから、と言われていますね。」という言葉を実証するためには、色々な生地の透過率を波長毎に調べなければならない。そのためには、光を波長毎に分解する分光器が必要である。そこで、私は
で分光器を作ったわけである。 前回は、分光器の出力をデジカメで撮影した。しかし、これでは赤外光の計測もしづらい。そこで、秋月で可視・赤外対応のCCDボードを買ってきた。これを前回作成したHIRAX一型分光器に取り付けて、計測を行った。名付けて、「HIRAX一型分光器CCD+」である。
 |
まずは、その分校計測出力例を示してみたい。下の写真は「CCDカメラで計測したスペクトルに、可視光の色対応を示すカラーバーを上に示したもの」である。これは前回と同じく、太陽光のスペクトルだ。水平軸が波長を示している。左が波長が短い領域であり、右が波長が長い領域である。可視光領域は左の1/3くらいの領域である。
 鮮鋭化処理をかけたもの  |
今回は、縦線状に見えるフラウンホーファー線が明らかに数多く見えるのがわかると思う。HIRAX一型分光器自体もスリット幅の改良などで性能がアップしてるのである。
それでは、まずはいくつかの材料の波長毎の透過率を計測してみたい。まず、使う材料は下に示すような色フィルターである。もちろん、こんな透け透けの材料で作った水着を着ている人なんているわけはない。これは、あくまで例である。
 |
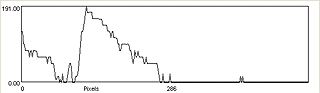
それでは、次に「HIRAX一型分光器CCD+」で計測した波長毎の透過性を示してみよう。まずは、赤色フィルタである。赤色フィルタを使用している部分は、使用していない部分に比べて、赤色(そして赤外領域)以外の波長がカットされているのがわかる。
 |
例えば、赤色が見えづらい人であれば、このフィルターは透過性が非常に低く、「透け透け度」が低いフィルターである、ということになる。また、赤外光は透過しているが、すごく長波長側では透過率がかなり低いことがわかる。
また、次が黄色であり、赤色フィルタよりも短波長側まで透過性が高くなっていることがわかる。そして、赤外光の透過性は赤色フィルタよりも高い。
 |
次に示す緑色のフィルタの場合は、緑の辺りの波長と赤外領域辺りの透過性が高いことがわかる。よく、ビデオカメラで赤外リモコンなどの赤外光を撮影すると、緑色に写ることがあるが、あれはこういった緑色のフィルタを使用しているのだろうか?
 |
次が青色フィルタである。赤外光の透過性は結構低い、こともわかる。
CCDカメラで計測したスペクトルに、色対応を示すカラーバーを上に示したもの |
色々、面白いこともある。例えば、赤色フィルタの透過特性と緑色フィルタの透過特性を比べると、重なり合う(透過性が高い)領域(波長)がほとんどないことがわかる。
  |
 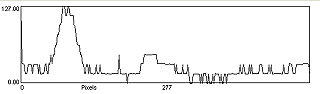 |
だから、赤色フィルタと緑色フィルタを重ねると、全然透けないわけだ。透過可能な波長領域がないワケである。こういうのを見ると、暗記用の赤色ペンと緑色下敷きの組み合わせを思い出してしまう。
 |
さて、こういう風に材料毎の透過性を計測できるようになったわけである。さらに、赤外線フィルタの透過性を見てみたい。赤外線の波長領域をまずは実感してみたい、ということである。赤外フィルタは赤外リモコンの発光部のカバーを使用してみた。下に示すのが、「赤外フィルタ= 赤外リモコンの発光部のカバー」であり、
 |
次が、赤外フィルタの透過性を示したものである。可視光はほとんど通さず、波長の長い赤外光のみ通過させているのがわかる。
 |
さて、あまりにも画像が増えてページが重くなってきた。今回は分光計測を行い、赤外線フィルターの分光感度を計測したところまでで終わりにしたい。次回は、色々な生地の透過分光計測を行う予定である。「色々な生地が可視光では透過率が低くても、赤外光では透けて見えることがあるのか」調べてみたい、と思う。
2000-04-16[n年前へ]
■透け透け水着の物理学 第二回 
水着の生地を手に入れろ
「透け透け水着の物理学」である。前回、
で「透け透け水着」を調べるための「波長別透過計測システム」を作ってみた。予算は総額4000円である。私からすれば、「透け透け水着」は予算をかけた大プロジェクトであると言っても良い。となれば、次は色々な水着の生地における「透け透け度」を調べたくなるわけであるが、その実験がなかなかできなかった。忙しかったせいもあるが、大きな理由は、
- 手頃な水着の生地が手に入らないので、実験ができない (材料の問題)
私の持っている水着はトランクスタイプで生地もかなり厚い。これでは、「透け透け」であるわけがない(それに、透け透けでは私も困るし、世間も困るだろう)。きっと、競泳用のビキニタイプのものであれば、薄い生地が使われているのであろう。しかし、私はビキニタイプの水着など持っていない。まして、レオタードなど持っているわけがない。
もちろん、他の人に借りるという手もないわけではない。しかし、相手が男であれ、女であれ、
「君の水着を少しばかり貸してくれたまえ。」と言うのは少々危険である。誤解される恐れがなきにしあらずだ。もちろん、実験に協力してくれる方がいらっしゃるならば、私のところまで「透け透け水着」を送っていただけるとありがたい。そういう方がもしいらっしゃれば、メールを頂ければ幸いである。とは一応書いてはおくが、送ってくれる人などきっといないだろう。
「いや、変なことをするわけじゃないんだ。」
「ただ、透け透け度を調べてみたいだけだから、気にしないでくれたまえ。」
というわけで、なかなか実験をすることができないでいた。もちろん、水着と似てそうな生地を頭の上では探してはいた。しかし、「服の生地」という観点から離れられないでいた。そのため、手近なところでは見つからないでいたのだ。結局、
- 服の生地を手に入れなければ、実験ができないだろう
しかし、数日前、怪しさ抜群の職場のK藤氏が私に囁いたのである。舞台は、夜の会議室だ。
K藤氏 「いやァ、hirabayashi君。透け透け水着の話なんだけどねェ。」なるほど、確かに雨傘の生地と水着の生地はよく似ている。水を防ぎ、風を防ぎ、ファッションを重視するのも全く同じだ。気づかなかった。気づかなかったのが恥ずかしい位である。もう、最後のK藤氏の
K藤氏 「ボクもやったことがあるんだけど、結構透ける生地ってあるんだよねェ」
私 「えっ、材料は何を使われました?」
K藤氏 「雨傘の布だよ、hirabayashi君。」
「雨傘の布だよ、hirabayashi君。」というセリフなどは、まるでシャーロック・ホームズの
「自明だよ。ワトソン君。」というセリフのようだ。むちゃくちゃ格好良すぎである。
しかし、よく考えてみると、何やら変なシャーロック・ホームズである。何故、シャーロック・ホームズが「透け透け水着の物理学」を探求するのだ?(人のことは言えないが…)
私 「ちなみに、K藤さん、どこでその実験をされました?」なるほど、想像するだけでスゴイものがある。色々な意味でスゴイ人だ。拳法の使い手でもあり、実は火星人だというウワサもある位のスゴい人である。いや、もしかしたらヒトですらないかもしれない。
K藤氏 「夜、部屋でね。一人でカメラを片手にね。ひッひッひッ。」(誇張無し)
そしてまた、この二人の会話に「何故、どんなことをするのか?」という疑問がないのが不思議と言えば、不思議である。そういったことは二人とも、不思議に思っていないようなのだ。
それは、さておき、私もK藤氏のように、雨傘の生地を使ってみたいと思う。その雨傘の生地の赤外線の透過率を確認してみたいと思うのだ。傘なら家にはたくさんある。何しろ、私は傘を持って外出することがない。雨が降ったら、外出先で傘を買うのだ。だから、家には傘が何本もある。
それでは実験を始めてみる。下の写真が家にあった傘である。どれも外出先で買ったものだ。
 |
そして、前回使ったCCDボードであるが、元々は赤外光投光部が付いていた。前回はその部分をあえて使用しなかったのであるが、今回はそれを使用してみたいと思う。
 |
それでは、このCCDボードを用いて赤外光を照射しながら撮影したものと、普通のCCDカメラで撮影したものでどの位「透け透け度」が違うものかを見てみたい。下に示す写真は左が普通のCCDカメラで撮影したものであり、右が今回のCCDボードを使って撮影したものである。雨傘の生地の向こうにある冊子(JAFMATE)の表紙の透け具合を見てもらいたい。
 |  |
 |  |
 |  |
 |  |
 |  |
白、桃、藍色の傘の生地は元々透け気味である。だから、普通のCCDカメラでも少し表紙が透けて見えた。しかし、緑色のものなどは普通のCCDカメラや人間の眼ではほとんど透けては見えない。しかし、赤外CCDカメラでは「透け透け」であった。また、茶色のものなども「透け透け度」が高かった。
もし、こんな生地で出来ている水着を着ている人がいるのであれば、これはもう「裸の王様状態」である(赤外線に感度を持つ眼の生物からすれば)。パラダイスとしか言いようがない。いや、そんなことはないか。
さて、「透け透け度」と色の相関は、色の波長を考えると、ある意味当然だろう。しかし、具体的な話は次回にしたい。生地の波長別の透過率を調べてから、ということにしておく。本来ならば、まずは先にそれをやらなければならない。白色光を用意して、雨傘の生地の波長別の透過率を調べなければならないところだ。
しかし、今回はそれができなかった。何故なら、基準光としての白色光、いつも使用している太陽が今日は出ていないからである。平日の昼間は実験ができない。しかし、週末の昼間にもやはり実験はなかなかできない。というわけで、いつか天気が良くて暇な週末が来たら、必ず「雨傘の生地の波長別の透過率」、言い換えれば、「色んな生地の透け透け度」を調べてみたい。
言うまでもないが、今回もまた「やましい気持ち」で動いているわけでない。私はただ「透け透け水着」に対する純真な好奇心(いや、科学的探求心と言い換えておこう)で動いているのみである。これから、夏に向けて「透け透け水着の物理学」はまだまだ進んでいく予定である。そして、水着を買う際の参考にして頂くことを切に切に望むのみである。
