2000-06-07[n年前へ]
■毛髪力のガウスの法則 
ハゲの物理学 「第五の力」編
現代の物理理論では四つの力が取り扱われている。その「四つの力」を示してみると、次の
- 重力
- 電磁気力
- 弱い力
- 強い力
ところで、これら「四つの力」に加えて、さらなる「第五の力」が測定されたという報告がされることがある。しかし、(少なくともこれまでは)それらはいずれも眉唾モノの実験ばかりであった。しかし、誤解されることを承知の上で、私も「第五の力」の提案をしてみたい、と思うのだ。
と書くと、鼻で笑う人がいるかもしれない。物理が大好きな人は私を小バカにするであろうし、物理を好きでない人はとたんに興味を失うであろう。しかし、そんな方々も少しばかり私の意見に耳を傾けるべきである。少なくとも、男性にとっては、この「第五の力」は重要な問題であるはずなのだ。いや、私は決して「理論物理=男性の領域」などと言うつもりはない。もうとうそんな考えはない。しかし、この私が提案する「第五の力」に限っては女性よりも男性にとって重要な「力」なのである。
私が提案する「第五の力」は、その名も「毛髪力」である。もう、おわかりのはずだ。これぞ、男性の人生をかけた大問題、「ハゲ」に関する問題なのである。「毛髪パワー」が「第五の力」なのである。
さて、そもそも今回「毛髪力」という「第五の力」に関する理論を提唱するにあたって、素晴らしき先達の研究があったことをここに書いておきたい。それはfreddie氏による「頭髪におけるキルヒホッフの法則」という素晴らしい研究報告である。「ボクテレビ」の2000/05/25に報告されている「物理と頭髪」の中にその詳細は記されている。
freddie氏は女性の視点から、女性のウィッグに関して、
そこで、僕は束ねられた髪の毛に関する基本法則をここに記したいと思います。と記している。私はこの「頭髪におけるキルヒホッフの法則」からインスピレーションを受けて、さらに男性の視点から理論を展開したい、と思うのである。
- 頭髪におけるキルヒホッフの法則:
「髪の毛を束ねる部分に頭皮側から入る髪の本数と毛先側へ出て行く髪の本数は同じ。」
先の「頭髪におけるキルヒホッフの法則」では、「頭皮側から入る髪」とあっさり書かれているが、男性の場合「頭皮側の髪」がそもそも無い場合がある。そう、「ハゲ」である。こう、私が書くのは、「毛髪力」は私にとって、人ごとでないからだ。自慢ではないが、私の髪はストレートのサラサラである。と言うと、羨ましがる人もいるかもしれない。しかし、それは違う。女性ならともかく、男性の場合は違うのだ。そう、絶対に違うのだ。何しろ、ストレートのサラサラヘアーは「ハゲへの片道切符」なのである。「恋の片道切符」はロマンチックであるが、「ハゲの片道切符」はそうではない。断じて、違う。違うのだ。
そもそも何故、我々の「長い友達」であるはずの「髪」が消えてなくなるのだろうか?そして、さまざまな「ハゲ頭」は一体どのような理由で発生するのであろうか?これらの疑問について、明快に答えた例は未だかつてない。ましてや、それを物理学的に考察した例は未だない、と思う。そもそも、毛髪とは何であるか明快に答えられる人がいるだろうか?いや、いないはずだ。
しかし、私はその答えを今日ついに見つけたのである。それが、「毛髪力」なのだ。この「力」が全ての物理現象を決め、我々の人生の喜怒哀楽を支配しているのである。毛髪、すなわち、「髪の毛」は「毛髪力」により発生する物理現象だったのである。
例えば、電磁気力で言えば、基本をなす方程式はマックスウェルの方程式である。次に、マックスウェルの方程式の一部を積分形で示してみると、このようになる。
![]()
- Kami!Home Page:ElectricField ( http://home.att.ne.jp/gold/kamikawa/electricfield/elefield.htm)
 |
この画面を見れば、一目瞭然だと思う。次の絵との相似性を感じるはずなのだ。
 |
この絵は頭皮から伸びる毛髪を示したものだ。電荷から伸びる電気力線と毛髪は実によく似ているものなのである。電磁気力と毛髪力は実によく似ているのだ。
ここで、先程の電磁気力と同じように、毛髪力に関するマックスウェルの方程式の一部を積分形で示すと、以下のようになる。
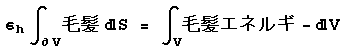
さて、さらに話を進めれば、重力であればそれは「重力子 = graviton」の交換により作用する。また、電磁気力であれば、それは「光子= photon」の交換により作用する。私は「毛髪力」に関してもこのような説明がつけられるのではないか、と考えている。
「重力子、光子」、すなわち、graviton,photonの名前の由来からすれば、その作用子は「毛髪子= moukon」と考えるのが自然だろう。私は日本語における「毛根」という言葉はこの「毛髪力」の作用子「moukon」の訛ったものではないか、とすら考えているのである。言語学的にも、「毛髪力」の妥当性が裏付けられた、と言っても良いだろう。
さて、毛髪は大抵の場合時間の経過にしたがって、少なくなっていく。いや、端的に言えば「ハゲ」ていく。毛髪力が低下していくのである。これも、先程の毛髪力のガウスの法則から考えれば、頭部内部の毛髪エネルギーが低下していると考えるのが自然である。ここで、私は、「頭部内部の毛髪エネルギーが低下」毛髪子の減少によるものだと考えている。毛髪子は何らかの変化により、他の粒子に変化するのだろう、と私は推察しているのだ。
「たいていの場合、ハゲた頭は光り輝く」ということから推察するならば、「毛髪力」は「光」に変化すると考えるのが自然である。すなわち、毛髪子は光子に変化していくのではないか、と私は現在のところ想像しているのである。毛髪力と電磁気力は表裏一体のものなのである。
 |  |
今回は、「第五の力」について論じてみた。唐突な話で判りにくいかもしれないが、この「ハゲの物理学」は私の人生と共に、まだまだ続く予定である。これから、先話がどう進んでいくかは私にも判らない。それは、私にとって吉と出るか、凶と出るか不安なところだ。実際のところ、それは誰にも判らないだろう。「毛髪力」の研究は今始まったばかりなのである。
2000-06-29[n年前へ]
■オッパイ星人の力学 
胸のヤング率編
本WEBサイトは「技術系サイト」というジャンルに分類されることが多い。が、実際にはどうも変な話題も多いように思う。しかし、私の観察によれば技術系サイトと呼ばれるところには必ずこの手の話が転がっているのである。実際、究極の技術系サイトの「Fast&First」でもというような素晴らしい話題はいっぱいあるし、同様に至高の技術系サイトである「今日の必ずトクする一言」の中でもという絶品の作品達が飾られている。
いや、つまり何が言いたいのかというと、変な話を書いてしまったことを正当化したいのである。技術系サイトには「とても身近なナゾ」への探求話が欠かせないのだから、変な話を書いたけど、勘弁しておいて欲しい、と言いたいのである。間違ってもエロサイトには分類して欲しくないのである。さて、どんな話かは下を読んで頂くことにして、もう少し言い訳を続けたい。何と言うか、この話を書き終えて何故か言い訳なしにはWEBに出せないような気持ちに、私はなっているのである。いっそのこと、この話は封印しようかとも考えた。しかし、先に示したように究極・至高の技術系サイトにもこういった?類の話があることに勇気付けられ、せっかくなので公にしてみることにした次第である。
以前、
で「できるかな?」読者の好みを調べてみた。それがこの下の円グラフである。 |
この円グラフから引っ張った部分は「エロ」である。これは、「IO = アイオー」ではない。「エロ= えろ=すけべぇ」である(前にも書いたけど)。 かように、「エロ」に興味を持つ人は多い。例を挙げるならば、「オッパイ星人」という言葉があるくらい、男の中には女性の胸に興味を持つ人が多い。私の友人の中には、ことあるごとに「おぉっ!!」と言いながら、通り過ぎる女性の胸を眺めるような輩までいるのである。しかもメガネをポケットからすばやく取り出し、サッとメガネをかけながら眺めるのである。まるで、ウルトラマンのセブンに変身する瞬間のモロボシダンなのである。「ウルトラセブンか、オマエは!」とか「モロボシダンがオッパイ星人に変身してどないすんねん!」と突っ込みたくなるほどである。
とりあえずこういう「オッパイ星人」のために、今回は「オッパイ星人の力学」について考えてみたい。具体的には、「バスト(なんか気恥ずかしいので言葉を変えた)の力学」について考えてみることにした次第である。
それでは、バストの力学について考え始めることにしよう。今回は、まずバストの基礎特性を調べ、次回にその運動力学について考えてみる予定である。
最初に、基本的な知識からだ。TVを観ていると、よく「Fカップアイドル」というような言葉を聞く。その言葉はよく耳にするのだが、実際のところその意味は知らなかった。そこで、調べてみると、ブラジャーのカップサイズは次の表のようにして決まるという。
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| アンダーバストと トップバストとの差 | 5.0 | 7.5 | 10 | 12.5 | 15 | 17.5 | 20 | 22.5 | 25 | 27.5 | 30 | 32.5 | 35 |
胸のバスト直下の部分の胸囲 = 「アンダーバスト」と、バスト部分の胸囲= 「トップバスト」の差からブラジャーのカップサイズが決まるわけだ(って今知っただけの知ったかぶりだけど)。Kカップなんてのもあるなんて驚きである。いやぁ、知らなかった。
しかし、「アンダーバストとトップバストとの差」が判っただけではバストの力学について考えるのは難しい。もう少し、取り扱いやすい量に変形させたい。そこで、次のような図を考えてみた。これは「胸部の断面図」である。上方向が人の前面方向である。
 |
バストを「半球状の物体」と仮定して、その「半球の半径 = r」を計算したいのである。そうすることで、バストの形状を計算しやすくなるのである。現実問題としては、バストがそうそう「半球状の物体」になるわけはないだろう。しかし、今回はとりあえず理想のドーム形状のバストを計算してみる、ということで許してもらいたい。
さて、上の極めて大雑把な近似をしまくりの図を見て頂くと判るように、
アンダーバスト = 4r + 4r + 2 胸のベース部分の厚さであり、
トップバスト = 2 r + 2 π r/2 + 4r +2 胸のベース部分の厚さである。したがって、
「アンダーバストとトップバストとの差」 = ( 2 r+2π r/2+4r+2胸のベース部分の厚さ)と計算してやることができる。そのようにして、計算した「胸のカップ数とr(cm)」を示したものが下の表である。ただし、実際には胸囲はそもそも下へ行くほど小さくなっているだろうから、アンダーバストはトップバストよりも胸のベース部分が35%小さいとして計算してみた。
- ( 4r+4 +2胸のベース部分の厚さ )
=2 r+2πr/2-4r
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| r | 2.8 | 4.3 | 5.7 | 7.1 | 8.5 | 10 | 11 | 13 | 14 | 16 | 17 | 19 | 20 |
これをグラフにしたものを下に示す。ほぼ直線的にバストのサイズが増加しているのが判ると思う。
 |
例えば、AAAカップだと半径2.8cmの半球状の物体だ。まるで、スーパーボールである。これなら、ブラジャーはいらないだろう。それが、Kカップともなると半径20cm程になる。ちょうどメロンを半分に切った感じだろうか?これはかなり、デカイ。
このr(cm)さえ計算できれば、あとは物体形状も体積もわかる。体積が判れば、当然のごとく重さも計算することができる。というわけで、次は重さについて考えてみよう。何しろ、バスとの運動力学を考えるならば、どの程度の質量を持つかどうか考えることは避けて通れないのである。
バストのほとんどの部分を占めるのはきっと脂肪だろう。脂肪の密度は水とほぼ同じだろう。そこで、脂肪の比重が1g/cm^3であるとして計算してやると、「胸のカップ数と胸一個あたりの重さ(g)」は以下のように計算することができる。(実はこの計算には後の松坂季美子の胸の重さに合わせるための定数、季美子定数を乗してある。)
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| 胸一個あたりの重さ(g) | 8.9 | 30 | 71 | 140 | 240 | 382 | 570 | 810 | 1100 | 1500 | 1900 | 2500 | 3100 |
なんと、Kカップでは「胸のカップ数と胸一個あたりの重さ(g)」が3000g= 3kg程もあるのだ。新生児が二人胸にぶら下がっているのである。この数字がホントなら大変な話だ。肩に負担がかかりんまくりである。1.5リットルのペットボトルを4本も胸にぶら下げているのだから、これは大変だ。なるほど、ブラジャーは必需品である。
上の表をグラフにしたものが下である。
 |
バストの質量は体積に比例する、すなわち、バストのサイズ( =長さ )の二乗に比例する。そこで、このような形状のグラフになるわけである。このグラフを眺めていると、Dカップ辺りを境にして、それより大きくなると胸や肩にかかる負担がシャレにならないくらいの大きさになると推測される。
ところで、地表にいる限り、当然バストも重力の影響を受ける。いや、むろん地表でなくても重力の影響は及ぼされるわけだが、そういう話は今回はおいておく。とりあえず、六本木を歩いている彼女も、ロサンゼルスにいる彼女も重力の影響を受けるのである。重力を受ければ、当然バストは重力で引っ張れる方向に垂れ下がってしまう。その様子を示したのが、次の図である。ここでは、「胴体から垂れ下がるバスト」を単純に「重りとバネで表すことができるモデル」だとしてみた。
 |
さて、一般的にバネの特性はフックの法則により
ここまで来れば、あともう一歩である。この式のkすなわち「バストに関するヤング率」を調べるだけである。「バストの垂れ具合」と「バストの重さ」を同時に計ってやれば良いのである。そうすれば、残るただ一つの変数、「バストに関するヤング率」を計算することができる。いやぁ、簡単、簡単....
といっても、実際のところここが一番苦労した。「バストの垂れ具合」と「バストの重さ」を同時に計らせてくれる人なんかどこにもいないのである。当たり前である。
そこで、ネットで検索をかけまくること数時間、ついに私は見つけたのだ。
そして、その質量 一個1kg!」
科学の徒として、私が丁寧に観察した結果、松坂季美子の「バストの垂れ具合」は約10cmであることがわかった。いや、もちろん科学の探究心のためであって、それ以外の気持ちはなかったことをここに誓っておこう。
その苦労の結晶のデータが、
- 松坂季美子はGカップ、バストの重さ=1kg、バストの垂れ具合10cm
この境界条件さえあれば、「バストに関するフックの法則」を完全に解くことができて、「バストに関するヤング率」も導き出すことができるのだ。ちょちょいのちょい、である。
その「バストに関するヤング率」を用いて計算してみた「胸のカップ数とバストの垂れ具合(cm)」を次に示してみる。
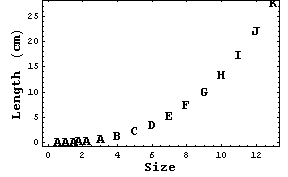 |
バストの「カップ」サイズの三乗に比例して、「バストが垂れていく様子」がよくわかると思う。この物理形状は「カップ」サイズに比例して、「バストの垂れ具合」は「カップ」サイズの三乗に比例するというデータを用いることにより、「究極のバストサイズ」を導き出せるのではないか、と私は考えているのである。が、それはまたいつかの話題と言うことにして、話を続けたい。
ところで、「バストに関するヤング率」は常に一定ではない。「おばあちゃんの垂乳根」を想像して頂けばわかるように、年をとれば「バストの垂れ具合」は大きくなるのである。
というわけで、さっきの計算結果をもっと若い条件、すなわちもっとヤングなヤング率で計算してみたのが次のグラフである。
 |
赤のもっとヤングなヤング率で計算してみた場合には、バストには張りがあって、バストの垂れ具合は小さいことがわかると思う。
さて、今回はバストの基礎特性を調べてみた。次回、この「バストに関するフックの法則」を用いて、「オッパイ星人の動力学」について考えてみたい、と思う。
追伸 : この話を書き上げた後に、恐る恐る回りの人に感想を聞いてみた。すると、
と言われてしまいました。ハイ、申し訳ありません。その通りでございます。返す言葉もありません。「こんなの作るくらいなら、
男の人のヤング率でも計算しなさいよ。」
2000-07-29[n年前へ]
■The Spirit Level 
Fair is foul, foul is fair.
この写真は九州阿蘇山の麓にある京大火山研究所を撮影したものだ。草で覆われただけの小高い丘の頂上に、この火山研究所の建物はまるで灯台のように建っている。それはあまりに広大な景色だったので、手元にあった小さなカメラではそのままでは全景を撮影できなかった。しかし、「その広大で、それでいて箱庭のような景色の一部分だけを切り出す」ということはしたくなかった。そこで、近くにあったカーブ・ミラーを通してその広大な景色を撮影してみた。カーブ・ミラーの凸面鏡で反射させることで、広角の撮影をしようとしたのだ。だけど、それはとてもぼやけたミラーをだったので、ねじ曲がってただのよく判らない写真になってしまった。だけど、それでもその景色の一部分を切り出すよりは良かったはずだと思っている。

この写真を撮影したのは、もう10年程前のことになる。その夏、私は二週間ほど中国・九州を旅行していた。それは普通の旅行ではなくて、観測のための旅行だった。GPSによる標高測定と水準測量による標高測定を同時に行うことで、ジオイド(重力の等ポテンシャル面のうち平均海面と一致するもの)の形状を調べようとする研究のための観測だった。といっても、私は単なる下働きだったから、何にも考えずただ昼は力仕事をして汗をかいて、夜は温泉に入ってビールを飲む、という何だかとても幸せな二週間だった。
GPSによる幾何的な標高測定に対して、水準測量による標高測定は各地点における水平面を基準として標高を逐次的に測っていく。ところで、そもそも標高とは鉛直方向に対する位置である。それなら、一体鉛直方向とは何だろうか?それは、水平面に対して垂直な方向としか言いようがない。水平面が定まれば、一意に決まるわけだ。それなら、それは確かなものかと言うと、それは違う。
何故なら、水平面自体が場所によって違うからだ。水平面というものは単純なものでは決してない。その周囲(または遠方)の質量の分布によっていともたやすく変わってしまう。重力場が変化するのだから、当然の話だ。水が重力に引っぱられて、重力の等ポテンシャル面を形成するのだから、質量分布によって重力場が変動すればその等ポテンシャル面である水平面は当然のごとく変動してしまう。
水平面・水準といったとても基本的な基準でさえ、地球の内部や外部の状態でよくわからなくなってしまう。それは、ものを伝える言葉だって同じことだ。そもそもの原動力や背景があってこその基準や言葉なのだから、中にどんなものを秘めているかで物事の基準自体が変わってしまう。人が見ているものだって、その背景できっとみんな違っていると思う。それらは実のところ、とてもあやふやなものなのだ。
だから、Fairなんてとても大切な言葉だって、人によってその意味するものは違うのだろう。例えば、今ここで"Fair"を例に出したのも、"Fairis foul, foul is fair."というマクベスの冒頭のセリフを知っていれば、「あぁ、そういうことか」とその意味するところを判るだろうし、その背景を知らなければ「何でそんなことをいきなり?」と感じるだけだろう。それだけのことだ。
ところで、水準測定を行う時の必需品が"Spirit Level"である。この"SpiritLevel"という言葉は、直訳した 「心・生命の高さ・水平」なんて意味では全然なくて、単なる「水準器」という意味だ。簡単に言ってしまえば、単に"Level"だ。"Spirit Level"もグラスの中のアルコールを傾けてみれば、その語源は想像がつくだろう。
確固とした基準になりそうな水準器でさえ、実はそんなに確かなものではないのだから、何かの確かなものがあるという思い込みこそ、実はとてもあやふやなものだろうと思うのだ。
2000-11-26[n年前へ]
■ブランコの中の∞(無限大) 
なんで一体漕げるのだろう?
公園のブランコというのは、何故かとても不思議な雰囲気を持っている。ホントにうるさいくてたまらないくらいのガキんちょ達が、アクロバットのようなスゴイ技を見せていたりする。それは、まるで上海雑伎団を見ているような気分になる。小さな子がなかなかブランコが漕げず、ブランコの上で宇宙遊泳のように四苦八苦しているのを見ているのも思わず笑ってしまうくらいに可愛らしいものだ。もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。
やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう?口で上手く説明できる人がいるだろうか?
それに、そもそも私たちはブランコを何故漕ぐことができているのだろう?
いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?という手紙で始まるのは加納朋子の「ななつのこ」だが、「何故、リンゴは落ちるのかという謎」と同じく、「ブランコの漕ぎ方の謎」だってとても不思議だ。いつも目にする公園のブランコを、私たちは一体どうやって漕ぐことができているのだろう?
いつだって、どこでだって、謎はすぐ近くにあったのです。
何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。
もちろん、「何でブランコの漕ぎ方が不思議なのさ?」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。
次の図は「ブランコを漕いでる子供」である。
 |
この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか?それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。
だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか?
次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、
- ブランコの動きの中心を向いている軸A
- 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B
 |
ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。
それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。
というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。
ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか? この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか?
 |
「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ!)上がれば、ブランコの速度はもとの速度の倍になるのである!
ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。
もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ!
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。
このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、
- 初期のブランコの速度 = 10
- 重心位置を高くして 10 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- 重心位置を低くして 10 X 1/2 = 10 (何てこったい、速度が半分になっちまったか!)
- 初期のブランコの速度 = 10
- 重心位置を高くして 0 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- そのあとブランコの速度 = 0
- 重心位置を低くして 0 X 1/2 = 0 (0が0になっても全然変わってないもんね!ヘヘン!)
人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。
まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。1万円×2=二万円では1万円しかもうからないが、一千万円×2=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。
もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。
そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね!となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。
というわけで、
- ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
- ブランコが上に行ったときにその姿勢を元に戻す
それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。
というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ
- 何もしない場合
- ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
- ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合
 → ブランコの動きはず〜と変わらない |
ブランコが上にきたあたりで座り込んだ場合  → ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」 |
ブランコが上にきたあたりで立ち上がった場合  → ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」 |
この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。
ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか? それとも、ちょっと考え過ぎかな。
2000-12-02[n年前へ]
■ブランコの中の∞(無限大) その1 
mail 子供がブランコをこぐということを「仕事をする」と考えます.仕事とは力に逆らって物体を移動させたりすることです.子供がブランコに乗っているとき、最下点に来た瞬間に速度は最大です.当然そのとき遠心力も最大になります.このタイミングでしゃがんでいる子供が立ち上がるということは遠心力に逆らって自分の体を移動させたと考えることができ、それは仕事をしたと考えられます. < Thank you. jun hirabayashi なるほど、判りやすい説明ですね。ただ、ちょっと気をつけなければならないのが、「 遠心力に逆らって自分の体を移動させた」という部分でしょうか。例えば、ブランコが45度の角度まで、つまり結構高く上昇した後に最下点を通過する時の遠心力を計算してみると、たかだか重力の六割弱に過ぎません。つまり、力あるいは仕事の割合から言えば、「重力に逆らって」という方が近いわけです。なので、結果的には単純に位置エネルギーを運動エネルギーに変換している、ということになるのでしょう。