1998-11-20[n年前へ]
■モアレはデバイスに依存するか? 
まず、以下のような2つの同心円画像をつくる。(なお、このような画像を簡単に作るために、Photoshop用のフィルターを作った。詳しくは「Photoshopの同心円フィルターを作る。」を参照して頂きたい。)以下の2つの画像は少し中心位置がずれている。また白く見えるところは255の値を持ち、黒く見えるところは0の値を持っている。(画像自体は512x512であり、表示の際に128x128に変換している。だから、この画像をそのまま保存して頂ければ、512x512のサイズで保存することができる。)
 |
 |
- 黒(0)+黒(0)=0(すなわち黒)
- 白(255)+白(255)=255(すなわち白)
- 黒(0)+白(255)=255(すなわち白)
- 画像1を白黒反転し、画像1'を作る。
- 画像2を白黒反転、画像2'を作る。
- 画像1'と画像2'を加算し、画像3を作成する。
- 画像3を白黒反転し、画像3'を作成する。
 |
それでは、以上の画像変換を小さい画像でまとめて表示してみる。
 |  |  |
ところで、上の3つの画像をそれぞれ平滑化してみる。すると、以下のようになる。
 |  |  |
以下でもう少し詳しく考えてみる。
重ね合わせにおける加算演算
下のような画像A、画像Bを考える。拡大してあるが、画像自体は1x2ピクセルのサイズである。また、白=255、黒=0とすれば、いずれも平均値は128程度である。 |  |
- 黒+黒=黒
- 白+白=白
- 黒+白=黒
 |  |  |
 |  |  |
 |  |  |
これに平均値も示すと以下のようになる。ここでは、LBPなどの紙に出力する際によく使われる、白=0、黒=255という表記をする。
 |  |  |
 |  |  |
 |  |  |
同じ128+128でも、結果は128になるか256になるかの2種類ある。同じもの同士であれば、結果は128であるし、そうでなければ256になる。そのために、平均値が保存されないのである。このように、平均値が保存されない、言い換えれば、加算演算の結果が線形でない場合にはモアレが発生することになる。もしも、マクロに見て「128+128=256」が多い領域があれば、それはモアレの黒い部分であり、そうでない所は比較的明るい部分であるということになる。
ロゲルギストの-モアレが生じる理由は黒さの非線形性による-という言葉はこの「128+128=128、と128+128=256という結果の違いがあり、それがモアレの原因である」ということを示している。
それでは、そのような現象「128+128=128という非線形性」が起きない状態を作ってみる。それには加算の結果である黒がサチらないようにすれば良い。
 |  |  |
 |  |  |
 |  |  |
これでは、いずれの状態でもグレー+グレー=黒、すなわち、64+64=128という風になっている。これは黒がサチっていないからである。すなわち、-モアレが生じる理由である黒さの非線形性さ-がない状態になっている。
それでは、この状態で計算実験Aと同じことをしてみる。それを計算実験Bとする。念のため、計算実験Aをもう一度示す。
 |  |  |
 |  |  |
 |  |  |
| 画像1の黒=0を128にした画像4を平滑化したもの | 画像2の黒=0を128にした画像5を平滑化したもの | 画像4,5を加算したもの |
モアレができていないのがわかるだろうか。これはグレー(128)+グレー(128)=256(もっと黒)で線形な関係が成り立っているからである。平均化された画像で濃度がどこも倍近くになっているのがわかると思う。
モアレのデバイス依存性
LBPではトナーが有る所、すなわち、画像が有る所はほぼ完全に影になる。例え、2枚重ねてもやはり影のままである。しかし、インクジェットならどうだろうか。OHPで使うと、黒といってもLBPに比べて薄い。1枚のOHPの黒よりも、2枚のOHPの黒を重ねた方がかなり黒い。ということは、「黒+黒=もっと黒」と同じである。したがって、OHPを重ね合わせても濃度が保存されている。すなわち、モアレが比較的に出来にくいことになる。ということは、OHPを何で作るかによってモアレの具合が変わることになる。付け加えれば、実際のOHPの場合には透過率を考えなければならない。透過率というものは単なる重ね合わせでない、具体的に言えば、加算演算でなく乗算演算である。それでも、話としては大体は同じことである。
今回はOHPの話に絞ったが、透過原稿でなく反射原稿についても同じである。むしろ、反射原稿の方が乗算演算でなく、加算演算である分、今回の話そのままである。したがって、一般的なモアレについてインク(もしくはそれに相当するもの)の加算演算の具合によって、モアレの発生具合が違うと考えられる。
また、話の単純のために白黒の話に限ったが、カラーのモアレなどについてもほぼ同じであろう。トナーとインク、また、混ざりやすいものと混ざりにくい物の違いなどでも面白い結果が出そうである。TVや液晶のようにほぼ線形の重ね合わせが成り立つであろうものと比較するのも面白そうである。
今回の話を考えている途中で、OHPの重ね合わせと干渉の共通点については、結構奥が深いような気がしてきた。そのため、別の回でもう少し詳しく考えたい。
1999-06-26[n年前へ]
■リモートカメラから世界をノゾこう! 
Macintosh用カメラ制御プログラムを作る
今日もニュースを探しに
MAQ?MAK?MAC! ( http://www.maqmakmac.com/)
を見に行くと、おやおや何やら見たことのあるキーワードがある。これが「デジャブ」という奴かと一瞬思ったが、そうではないようだ。本WEBについての記載がある。ビックリだ。いや、ホント。
自分の興味の趣くままにやっているサイトではあるが、好きなサイトで「面白い」といってもらうと、とても嬉しい。また、そこから辿り
WebCatchを見る。「ノーラ」氏の文章には頭が下がる思いである。
MAQ?MAK?MAC!には「もっとMacintoshに関連した話題が多ければ良いのになぁ?。 」とも書いてある。そう、私もMacintoshの話題が少ないとは思っていたのだ。Macintoshが多い私の職場の人々からも(次回の話への伏線)言われ続けてきたことなのである。ならば、MAQ?MAK?MAC!( http://www.maqmakmac.com/ )登場記念にMacintoshを使った話をやってみたい。
というわけで、今回は急遽Macintoshを使った実験の話である。物語は、こんなジャンクを手に入れたところから始まる。ごくたまに、秋葉原でも見かける。もし見かけて、かつ、安かったら、迷わず「買い」だ。LEGOのMindstormsなんかと組み合わせたら、かなりかっこいいはずだ。
 |
これが、「Canon製ビジュアルコミュニケーションカメラ」である。シリアル通信でカメラの向きやズームピントを変えることができるものである。上下左右に首を振ることができるし、ズームやマクロ撮影も可能だ。発売当初は20万円位もしていたものだ。この後継機種も出ている。
これを使って、何か面白いことをしてみようと思った。いや、はっきり言ってしまえば、ネットワーク上のMacintoshにこのカメラをつなげて、それを他のコンピュータから制御しようにしたい。今でこそ、そういったWEBサイトも多々あるが、今回の話の実験を行った時(確か2,3年前)にはまだ少なかったのだ。
このカメラはジャンクとして手に入れたので、ソフトも何も付いていない。しかし、シリアル通信のコマンドは何とか判明したので、制御プログラムを作ってみた。といっても、単なるシリアルポートへコマンドを送りつけるプログラムである。
プログラムはここに置いておく。名前もずばり、「のぞき見君」である。もちろん、Macintosh版なのでWindowsでは使えない。
のぞき見君 0.1anozokimi01a.sit ( sit形式 332kB )
正式にこのカメラを持っているユーザーにも今回のような用途(イヤな用途である)であれば、このソフトはきっと役に立つと思う。
今回(といっても作成したのはずいぶん昔だ)作成したプログラム「のぞき見君」の起動画面が下である。
 |
下がメニュー画面である。画面を見れば判ると思うが、全てのメニューをコマンドキーを用いてキーボードのみでコントロールするようにしてある(これが素早く使うためのミソだ)。
 |
このソフトをインストールして、Macintoshとカメラをシリアルポートでつないで、また、ビデオ出力もMacのビデオ入力につなげばとりあえず、接続完了だ。これで、Macintoshから自由自在に制御できるビデオカメラの完成だ。
さて、次はネットワーク経由で制御するための作戦だが、何ら苦労(私の)は必要ない。例えば、innfo-macに登録されているremote-mouse-keysというようなソフトを使えば、ネットワークにながっているMacintoshのキーボードやマウスを制御することが簡単にできる。
ftp.flashnet.it/mirror/8/sumex-aim.stanford.edu/comm/remote-mouse-and-keys-10.hqx
ビデオ画面の転送はもちろん、Cu-SeeMeでも使えば良い。最近はその手のソフトも多いだろう。それでは、今回のプログラム群を使った構成図を以下に示す。Macintoshはネットワークの自由度が高いので色々な使い道がある。
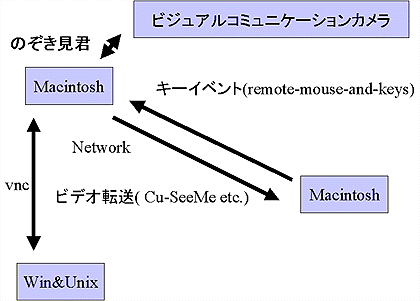 |
remote-mouse-keysとCu-SeeMeの組み合わせが軽くてお勧めなのだが、今なら
vnc (http://www.uk.research.att.com/vnc/index.html )
を使うといったやり方もアリだろう。これなら、プラットフォームをあまり選ばないので、WindowsやUnix系OSからでも制御できるし、一つのソフトで制御もビデオ画面転送も済んでしまう。ただし動作がまだ重いとは思う。
それでは、今回のソフトを使った顧客例を紹介しよう。
それは私の職場の「ち*の」氏の使用例である。彼は結婚間近であった。いずれ妻と住む新居にPowerMacintosh6100がこのカメラとともに設置してあった。彼は家の戸締りが気になって、職場から家にPPP経由でRemote-Accessを試みた。彼のPowerMacintosh6100は電話がかかってくるとともに起動音を発し、起動した。そして、彼は職場からの制御により、家のPowerMacintosh6100につながったカメラは首を起こし右へ左へと方向を変え、戸締りのチェックを始めた。彼の目的は達成された。家の戸締りは完璧であった。
ただ一つの問題は、彼は知らなかったが、結婚間近の恋人が掃除をするために新居を尋ねていたことである。彼女の目の前で、電話の音とともに勝手にMacの電源が入り、「ジャーン」という音を発し、そして、そこにあるカメラが「ウィィィーン、ウィィィーン」と右へ左へ動き始めたのである。「ひどい恐怖を感じました」、と彼女は後に語ることになる。
その後、彼の結婚がはたして実現したのか、それとも実現しなかったのかはここでは明らかにしない。
2000-02-02[n年前へ]
■日出ずる処のダイナブック 
東芝ノートの発表日の秘密
東芝の作るノートPCはアラン・ケイが考えた"Dynabook"という名前で呼ばれる(日本では)。その名に恥じないように、東芝もノートPCに関しては力を入れまくりのハズである。
私も歴史は浅いが数台にわたって東芝ノートのユーザーである。ポインティングデバイスなどは、東芝のトラックポイントとボタンでないと耐えられない体になってしまった。いや、本当に。
しかし、使い始めて年月が経つと性能の低下や不具合が出てくる。特に、ケースが割れまくる機種などを使っていると、なおさらである。
そうなると、どうにも新製品が気にかかってくる。「早くいい新製品が出ないかな」と熱望するようになるのである。
そういう気持ちは誰しも抱くと思われ、NiftyのフォーラムやWEB上の掲示板を眺めてみても、新製品の噂情報は数多く溢れている。
中でも、
- どんな新製品が ( What )
- いつ出るのか ( When )
だからといって、掲示板で「私はいつPCを買えば良いのでしょう?」などと尋ねたりすると、
「欲しいときに買えェ。」 (By スタパ斎藤)などと言われること必至である。
「そんなことは自分で決めろ。」
だから、新製品を買うべきか買わざるべきか、というジレンマに私たちは頭を悩まされることになる。まるで、ハムレットである。
そもそも、このジレンマの理由は新製品の発表が前もって知ることができないという点にある。いつ・どんな新製品が出るかどうか判っていれば、あとは自分の判断で決めれば良いのである。
このジレンマは東芝の青梅工場に忍び込んだりすれば即座に解決できる。しかし、その場合、今度は「囚人のジレンマ」を考えなければならなくなってしまう。このような問題点のために、「東芝青梅工場に忍び込む」方法は採用すべきではない。
そこで、よく考えてみる。先の
- どんな新製品が ( What )
- いつ出るのか ( When )
今回は、東芝のノートPC製品の発売日を統計的に調べ、そこに隠れている規則性を明らかにしてみたい。というわけで、今回は新製品が欲しい人たちに贈る研究報告である。
まずは、
- Notebook Center ( http://www.kamikura.com/notebook/)
- 機種 発売日
- Libretto50 1997/1/7
- Satellite220 1997/5/8
- Libretto60 1997/6/24
- Libretto70 1997/10/29
- Satellite 300/305/310 1998/2/2
- Libretto100 1998/3/5
- TECRA780 1998/4/2
- Satellite 1998/5/11
- Satellite325/320 1998/7/27
- Satellite4000 1998/8/3
- Portege3010/3000 1998/8/12
- TECRA8000_Satelllite4000X/4010X_PORTEGE7000LibrettoSS1010 1998/10/22
- Satellite2510 1998/11/5
- PORTEGE3020 1999/1/7
- Satellite2520 1999/1/13
- SS3300_Satellite4000 1999/1/26
- SS7020X 1999/4/13
- DynaBook4050X/2540S 1999/5/12
- SS3330 1999/6/3
- Satellite4100X 1999/6/15
- Librettoff1100_DynaBookSS3380 1999/6/28
- DynaBook2060 1999/8/5
- Satellite2590X/2100 1999/10/14
- SS3330V 1999/10/26
- SS3380V 1999/12/7
- Satellite4320/4260/2140 2000/1/19
- Dynabook 2000/1/26
 |
ここで、このグラフの曜日軸は、
- 0 日曜日
- 1 月曜日
- 2 火曜日
- 3 水曜日
- 4 木曜日
- 5 金曜日
- 6 土曜日
- 火曜日〜金曜日
何故、月曜日に発表しないのか、このナゾをと某メーリングリストで質問した所、幸いにもその答えを教えて頂いた。それは日付変更線と関係していたのである。
もし、日本で月曜日に新製品を発表すると、日付変更線の向こう側のアメリカではまだ日曜日である。すると、全世界で同時発表ということができない。東芝は全世界を視野におくので、全世界同時発表ができる火曜以降が良い、というわけである。その結果として「火曜日〜金曜日」になるというわけである。
日出ずる処のダイナブックが故なのである。
また、今回の結果では発表月は1,10月が多かった。
そこで、今回の結論は
- 「東芝ノートPC発表は1,10月の週の中頃に期待しろ」
- 「東芝ノートPC発表は月の始めの金曜日に期待しろ」
P.S.メモリー容量の上限をもっと多くして下さると幸いです > 東芝さま
2001-03-04[n年前へ]
■柿ピーのシーソー・ゲーム 
柿とピーナツの供給バランスを考える
結婚しようとするカップルが少しばかり気にした方がよいのが、「柿ピーの好み」である。知らない人がいるとは思えないが、念のために書いておこう。柿ピーと言えば、柿ピー= 柿の種 + ピーナッツであって、亀田製菓の大ヒット商品である。そして、何と言ってもビールの安上がりのおつまみだ。
 |
この「安上がりで手軽なおつまみ」というところが、結婚しようとするカップルにはとても重要である。何故なら、結婚する前のカップルであれば洒落た店で飲むことも多いかもしれないが、結婚後はなかなかそうはいかない。いつの間にか手に持ったワイングラスは缶ビール(しかも発泡酒)に変〜身し、「テーブルの上の豪華な食事」はちゃぶ台の上の亀田製菓の柿ピーにバケラッタしているのである。
そうなると、かつては「このソースとても美味しいよね。うふっ。」なんて言っていた二人も変わらざるをえない。そりゃそうだ。柿ピーを目の前にして、気取ってみてもしょうがないわけだ。そんな時、こんな会話に走りがちである。
「柿の種ばっか、食べないでよ!」そう、柿ピーがなまじ「柿の種 + ピーナッツ」なので、片方がどんどん減っていったりすると、これがもう大変。かつては、ワインを片手に愛を語らっていた二人も、今やビール(しかも実は発泡酒)を片手に食い物の奪い合いをすることになるのである。
「オマエこそ、ピーナッツどんどん食えよ!」
これが、カップルの二人がとても似たもの同士で、「私達二人とも柿の種がスゴ〜ク好きだから、ピーナッツなんかいらないの。だから、- 柿の種だけが100%入った柿の種 - を買うの!」なんて感じなら、もちろんノープロブレムだろうし、あるいは、「ぼくらは、ピーナッツだけを買うのさ!」という感じのカップルでも同様だろう。
 |
あるいは、もう「ぼくは柿の種が好きだけど、きみはピーナッツが好き。二人は違っているから良い組み合わせなのさ。柿の種はぼくがどんどん食べるから、君はピーナッツをお食べ」なんてカップルでもいいだろう。こちらも、「ひとまずは」ノープロブレムである。つまりは、全く同じが正反対のカップルであれば、大抵の場合ほとんど問題はないのである。
しかし、「柿ピーは柿の種とピーナッツが適当な割合で入っているから良いのさ」なんていうグルメ気取りのカップルがいたりすると、大変である。
「アンタの食べる割合、少しおかしくない?」となるのは必至である。この数分後には、巨人の星の一徹父ちゃんのごとく、ちゃぶ台はひっくり返されているのに違いないのである。柿ピーの割合恐るべしだ。
「何言ってんだよ!オマエの方が柿ピー食べ過ぎだってんだよ!」
「そんなことないわよ!」
そして、しかもこれが理系カップルともなれば、もう最低だ。
「柿とピーの割合は7:3で食べなさいよ!」という具合になるに決まっているのだ。このままいくと、柿ピーを前にして離婚談義にもなりかねない。なんともオソロシイ話である。(* ピー柿は7:3でピーナツの方が多い。そんなのが実在することが私にとっては驚きである。)
「違うだろ、6:4が適正値に決まってるだろ!」
「そんなにピーナッツを食べたいなら、柿ピーじゃなくてピー柿*にしなさいよ!」
「別にピーナッツが過半数を超えるほどがイイって言ってんじゃねぇ〜!」
「何よ、もっと定量的に話しなさいよ!」
そういうわけで、「柿ピーの好み」「柿ピーの割合」「柿ピーの消費の割合」なんていうものは、結構結婚しようとするカップルには重要なのである。結婚しようとするカップルはぜひとも心して聞いておいてもらいたい。とはいえ、モテモテ度テストで
「女にモテない、というより、女に興味がないオマエ。今、一番気になることがドリキャスの値下げだったりなんかしない? まーそれも人生だけど、モテたほうがおいしいことは多いぜ? もうちょい女に関心持てよ。」と判定された私が言っても説得力がないか。
ところで、そもそも柿ピーの割合はどのくらいが普通なのだろうか?WEBで検索してみると、柿ピー10に対して
- 柿の種 : 7〜6
- ピーナッツ : 3〜4
そこで、試しに私も手元にあった小袋入り亀田の柿ピーの中身を調べてみた。調べたのは「小袋入り亀田の柿ピー」である。
 |
この一袋の中身を開けてみると大体こんな感じである。
 |
もちろん、単に数えても良いわけではあるが、「クダラナイことに、無意味なほどに大ゲサな道具を使うのがこのサイトのポリシー」でもあったりするので、まずは画像処理ソフトを使って柿の種とピーナッツの個数をカウントしてみた。使ったソフトはUTHSCSAImageTool である。PCベースでフリーでお手軽で粒子カウントとなるとこのソフトになるだろう。もちろんNIH-imageベースのScionImagePCという選択肢もないわけではないが、こと粒子カウントになるとはるかにImageToolの方が使いやすい。マクロの取っつきやすさ(機能は較べものにならないほどおちるが)もNIH-image系よりも上である。
さて、まずは上の画面内で柿の種を粒子カウントしてみたのが次の画面だ。この画面では見つかった柿の種は赤い縁取りがされ、個数がマーキングされていることがわかると思う。ちなみに、この画面内では93個の柿の種が見つかった。しつこいようだが、「数えた方が早いだろっ!」というツッコミはこの「できるかな?」では厳禁である。
 |
同じようにして、ピーナッツをカウントしてみたのが次の画面である。この画面では、ピーナッツは23個見つかった。
 |
すると、個数ベースでピーナッツが23/(93+23) = 20%で、残りが柿の種で80%ということになる。柿ピーの割合は大体8:2であったことになる。確か、WEBの亀田製菓に関する情報では
「柿ピー」のブレンドは、柿の種6に対してピーナッツ4が基本と書いてあったような気がするので、今回の8:2というデータは測定誤差、とその他の何らかの誤差が重なったものだろう。いや、そんな誤差はどうでも良いか。
ところで、大きな袋に入った柿ピーを食べながらよく考えることがある。私は柿の種が大好きなので、柿の種ばっかり選んで食べていくと、袋の口近くの上の方にはピーナッツばかりが残り、明らかに袋の場所ごとに柿の種とピーナッツの割合が異なってしまっていることがよくある。この柿の種とピーナッツの割合の時間的・空間的変化は一体どうなっているものだろうか?そこで、今回その「ピーナッツの柿ピーに占める割合の時間・空間的変化」について、少し考えてみることにした。
まずは簡単に判るように、袋の中から均等に柿の種とピーナッツを「柿ピーの割合を適当な割合で」食べていった場合、「ピーナッツの柿ピーに占める割合」は次の図のようになる。この図は横軸が時間で、縦軸がピーナッツの柿ピーに占める割合である。
緑 : 柿ピーを8:3の割合で食べた場合  |
今回の場合柿ピーは8:2で入っているので、青の場合のように柿ピーを8:2の割合で食べていくと、時間にして10分後に柿ピーがなくなるまで、ピーナッツの柿ピーに占める割合は20%をキープしたままである。しかし、(少しばかりピーナッツが好きな人が)柿ピーを8:3の割合で食べてしまうと、つまりピーナッツを過剰に食べてしまうと、どんどんピーナッツの割合は減ってしまい、ついに8分経過後にはピーナッツが袋の中から無くなってしまうのである。つまり、あとの2分は悲しみと共に柿の種を食べ続けなければならないのである(私は柿の種が好きなので悲しくもなんともないが)。
じゃぁ、袋の中の空間的分布も考えてみたらどうなるか、というのを次に計算してみた。まずは、袋を大きく二つに分けて、袋の入り口で適当な割合で柿ピーを食べた後、袋の奥から袋の入り口の方へ柿ピーを持ってくる。また、その際に適度に柿ピーをかき混ぜる。そして、柿ピーがなくなるまで柿ピーの割合の変化を調べてみるのである。ちなみに、IE4以降+Excel2000以降?の人であれば、ここをクリックすれば、その計算シートで遊ぶことができると思う。
例えば、「柿ピーを8:2の割合で食べた場合」と「柿ピーを8:5の割合で食べた場合」のピーナッツの柿ピーに占める割合の時間・空間的変化を調べてみたのが、次に示す結果である。ちなみに、このいずれも横軸は時間である。また、時間軸にして30前後の時点で柿ピーは完全になくなっている。
 ちょっと計算上の誤差が大きいが、それはちょっと無視してもらいたい。 |
さて、左の「柿ピーを8:2の割合で食べた場合」、つまり本来の柿ピー比と同じ割合で食べていった場合には、入り口近くでも奥の方でも柿ピーの比率は変わらない。そして、入り口の方から柿ピーを取った分を、奥の方から補給しているので、奥の方では時間軸20の時点で空になってしまっている。左の図でピーナツの割合がゼロになっているように見えるのは、実は単に柿ピーがなくなっただけなのである。そして、入り口近くの柿ピーが時間軸30の時点で空になっているまで、柿ピーの比率は変わることはない。当たり前だ。
では、「柿ピーを8:5の割合で食べた場合」はどうだろうか?つまり、本来の割合よりもピーナッツを多く食べがちな人の場合だ。そんな場合の右を見てみると、奥の方は単に入り口近くに柿ピーを補給しているだけなので、柿ピーの割合は変わらないままだ。しかし、入り口近くではあっという間にピーナッツの割合が減ってしまっている。ほとんどなくなっている、といっても良いくらいの状態である。つまり、ピーナッツ大好き人間にとっては、手の届く袋の入り口近くには全然ピーナッツがないという、拷問状態なのである。周りに女子校や共学の学校はあるけど、自分の通う学校が男子校だったみたいなキツイ状態である。ちなみに、私は高校時代に私服の共学の学校に通った結果、制服の女子高生に強い強い憧れを抱くに至ったことを否定できなかったりするのである。
話を戻して、それでは「袋を適当にかき混ぜながら」、「柿ピーを8:5の割合で食べた場合」はどうなるだろうか?というのが次の結果である。こうすると、奥の方のピーナッツもどんどん消費されているのがわかる。入り口近くも奥の方も、同じようにどんどんピーナッツの割合がどんどん減ってしまい、時間軸15の時点で完全になくなってしまっている。あとは柿の種がなくなる時間軸30の時点まではもう柿の種と向かい合うだけの人生なのである。ツラすぎる(ピーナッツ好きの人にとっては)。私の知人のオッパイ星人が結婚後に妻から、
*一部、不適当な発言がありましたことをお詫びします。
 |
つまりは、ピーナッツが食べたいからといって、あまり柿ピーの袋をかき混ぜるのは良くないということなのである。もちろん、短期的にはピーナッツがたくさん食べることができて良いわけであるが、長期的に見ればその後の長い「柿の種人生」が待っているのである。それが端的にわかるのが、次の「ピーナッツをどれだけ食べているか」を示す結果である。
この結果の中で、上の方に示した「柿ピーの袋をかき混ぜない場合」では、結構最後までピーナッツを細々と食べていけることがわかるだろう。柿ピーがなくなるのが時間軸で30前後の時点であるが、その少し前23位の時点までピーナッツを食べていけるのである。それに対して、ピーナッツを早く食べたいばかりに、柿ピーの袋をかき混ぜまくりの下の「柿ピーの袋をかき混ぜた場合」には、時間軸で13前後の時点でもうピーナッツがなくなってしまっている。もう、コイツには「柿の種人生」しか残されていないのである。
| 柿ピーの袋をかき混ぜない場合
結構最後までピーナッツを細々と食べていける |
| 柿ピーの袋をかき混ぜた場合
なんとも、太く短くのピーナッツの食べ方である… |
とはいえ、柿ピーの袋をかき混ぜながら太く短くピーナッツを食べるか、それをじっとガマンの子で細々と最後までピーナッツを食べるか、どっちが良いかは難しいところだ。ちなみに、私はかき混ぜまくりで柿の種を食いまくり、残ったピーナッツは人にプレゼントするというとても良い性格である。だったら、100%柿の種を買えって感じであるが、売店には置いてないことも多いから、しょうがないのである。
というわけで、今回はビール(やっぱりあくまで発泡酒)を左手にそして柿ピーを右手でつまみながら、酔っぱらった頭で(いつものことだが)、ツマラナイことを考えてみた。モノが本当の柿の種であればオチて芽が出るのが普通なのだけれど、今回の柿ピーの話はオチがあるわけでも芽が出るわけでもない。酔っぱらいのタワゴトだから意味なんか全然ないのである。と、日記には書いておこう(意味不明)。
2001-10-13[n年前へ]
■今日見た景色 ミドリのカケラ 
マクロはこんな感じ。ミドリのカケラ。(リンク)

