1998-11-12[n年前へ]
■無限音階を作ろう 
上昇し続けるって何ですか?
無限音階を作りたい
無限音階というものがある。ド・レ・ミ・・・と音がどんどん高くなっていくように聞こえるのだが、いつまでたっても終わらず、ふと気づくとずっと前と同じような音の高さだというものである。Escherの無限階段の版画は有名だが、あれの音階版である。とにかく、無限音階を作ってみようというのが今回の目的である。参考までに、Eshcerのことに関しては藤原康司氏のWEBhttp://www.pluto.dti.ne.jp/~fwhd5468/に詳しい情報がある。 ちなみに、このような版画である。
 |  | 「上昇と下降」(左図、1960年作) 「滝」(右図、1961年作) |
無限音階の仕組み
人間の聴力にはもちろん周波数特性がある。ニコンの補聴器のWEBhttp://www.nikon.co.jp/main/jpn/society/hocyouki.htm
によれば20Hz-20kHzが通常聞こえる周波数の範囲であるという。例えば、CDのサンプリング周波数はが約40kHzであるのは、この20kHzの倍だからである。つまり、ナイキスト周波数による。
もし、ある高さの「ド」の1オクターブ下、そのまた下、...それだけでなく、1オクターブ上、そのまた上...が一度になったら、人間の耳にはどう聞こえるだろうか。それは、やはり「ド」である。その時のスペクトルはこんな感じである。なお、横軸は2をベースにした変形の対数軸である。また、実際には「ド」ではない。
 |
それでは、そのような「レ」が鳴ったとしたら?もちろん、それも「レ」である。そのようにして、「ドレミファソラシド」とやるとどうだろう?最初の「ド」と最後の「ド」は全く同じになっている。しかし、人間の感覚としてはどんどん音の高さが上昇していくように感じる。これが無限音階の仕組みである。
図で示すとこのようになる。なお、下の図中で水色は人間の耳に聞こえる周波数領域である。また、振幅はたんなる相対値である。
 |
 |
 |
 |
 |
作成した無限音階
今回は12音の平均率音階を用いている。音階そのものについては「音階について考える」という別の話である。また、基本波形としては正弦波を用いている。20Hz以下の正弦波を基本波形として、その倍音を20kHz超まで均等に足しあわせたものをただ作っただけである。正弦波を用いたのは話を単純化するためである。ここに今回作成したMathematicaのNoteBookを置いておく。また、下が作成する途中のデータである。どこか間違っているような気もする。少し不安だ。
 |  |
 |  |
さて、これが作成した無限音階である。それっぽく聞こえるだろうか。
1999-02-14[n年前へ]
■感温液晶でNotePCの発熱分布を可視化する 
熱いところで感じてみたい St.Valentine 記念
東急ハンズで実験材料をいくつか買った。その中から、感温液晶シートを使って計測を行ってみたい。
色が変わる材料というものは多い。温度により物質の色がかわる現象はサーモクロミズムと呼ばれる。光により色が変わるサングラスのような現象の場合はフォトクロミズム呼ばれる。けっこう、色々な応用を見かける。
通常の感温液晶はコレステリック(Cholesteric)効果により反射光のスペクトルが変わるため、色が変化する。
これが感温液晶シートである。よくで見かけると思う。
 |  |
さて、それでは感温液晶を使っていくつか測定を行ってみたい。まずは、NotePCの発熱分布を調べてみる。最近のNotePCはかなり熱くなるものが多い。暖かいというよりもアッチッチ状態になるものさえある。
それでは、
- Toshiba Libretto50
- Panasonic Let'sNote mini(AL-N4)
いずれも、感温液晶シートをNotePCの上に載せることにより、評価を行っている。今回は発熱分布を知ることが目的であるので定量的な評価は行っていない。もし、温度を定量的に行いたいのであれば、色と温度の対応曲線をあらかじめ測定する必要がある。
以下に結果を示す。
 |  |
 | 左上:上面 右上:上面の発熱分布 左下:下面の発熱分布 |
 |  |
 | 左上:上面 右上:上面の発熱分布 左下:下面の発熱分布 感温液晶シートのサイズがA4であるため、Let'sNote miniにちょうどフィットする。 |
Libretto50ではPCカードのNICを右に挿しているため、キーボードの右側部分の発熱が大きい。また、下面ではハードディスク部分の発熱がわかる。また、ク*ックア*プしているせいかかなりアッチッチである。
Libretto50,Let's Note miniいずれにおいても液晶のドライバーがある部分(液晶の左)は発熱が激しいのがわかる。
本来ならば、愛用しているTOSHIBA Portege320でも計測を行いたい所だが、ただいま長期入院中である。間もなく使用1年になるが、これまでに入院3回を経験し、入院期間は計2ヶ月にわたる。昔の小説家もビックリの病弱さである。他の使用者の話を聞いていても実に不安定な機種のようだ。一体、疲労骨折を経験していないPortege320というのは、はたして存在するのだろうか。あぁ...
今回は手元にあったNotePCでのみ測定を行ったが、近所の協力の下に色々なNotePCの発熱分布を調べる予定である。特にパームレスト周りの発熱分布などは割に軽んじられているだけに、興味がある。
今回は感温液晶を使った温度分布の簡単な可視化をしてみた。同じような測定は色々してみる予定である。
感温液晶と同じように、温度で変化する材料は多い。例えば、FAXでよく使用される感熱紙もそうである。
他にも、RICOHの熱可逆性情報表示フィルム
http://ext.ricoh.co.jp/saiyo/sin/prof/eyes/page4_2.html
などもそうである。
これなどはお店のポイントカードなどでよく見掛ける。私の財布から探してみると、オートバックスのポイントカードがこれと同じようなものである。70-130℃位の温度変化により透明度を変化させる材料である。これ位の温度であると、真夏の車中にカードを放置するとどうなるか心配なところである。
今回の情報に関連するWEB一覧
- 伊藤のホームページ(http://www.infonia.ne.jp/~itous/)
- 岡山県教育センター(http://www.pref.okayama.jp/kyoiku/sido/edu_cent/seminar/rika/rikasho/zikken.htm)
- お湯で変色するサーモクロミズム化合物をつくる(高橋 正)(http://www2b.biglobe.ne.jp/~murasho/news22.htm)
- 液晶について(http://www.osakac.ac.jp/labs/fujita/asai/ekisyo.html)
- 感温液晶を用いた非定常熱伝達の計測システムの基礎的研究(http://village.infoweb.ne.jp/~fwhz0564/kenkyu.htm)
- 感温液晶マイクロカプセルによる可視化(http://koneeko.linux.or.jp/AandO/gfd_exp/exp_j/tech/elc.htm)
1999-08-25[n年前へ]
■インラインスケートの力学 (初心者編) 
つま先立ちの180°ターン
今回は滑る道具の話である。シャレではないが、私はスキーが好きだ。そして、最近インラインスケートを始めた。使っている道具はこんなものである。
- Dynastar AssaultSuperior
- Hart FreeLaunch
- K2 BING AIR
| Dynastar AssaultSuperior (右) Hart FreeLaunch (左) | K2 BING AIR |
 |  |
それぞれの滑走接地部の長さはDynastar AssaultSuperiorが185cm程であり、Hart FreeLaunchが110cmである。K2BING AIRは26cm位だ。
Dynastar AssaultSuperiorの長さを1とすれば、Hart FreeLaunchは長さが0.6程度である。半分とは言わないが、かなり短い。75cmも違う。しかし、この程度の長さにしたくらいではそれほど不安定になるわけではない。特にHart FreeLaunchは安定性が抜群である。私もゲレンデで普通に滑っている限りでは、遅い方ではないと思うが、特に不安定になることはない。不安定だと感じるのは、コブ斜面で、なおかつ、雪が積もってコブの形状が見えない場所を滑る場合などである。それほど、安定感があるのである。
そして、スキー板が短いため、ターンのしやすさといったら素晴らしいものだ。1つのコブの上で、2回3回とターンが出来る。
さて、今回の本題のインラインスケートはと言うと、かなり接地長さが短いため、さすがにスキーに比べて不安定さを感じる。とはいえ、思ったよりも不安定ではなかった。(初心者の頃の)スキーで曲がる時のことまで考えたら、もしかしたら、スキーよりも転びにくいかもしれない。急角度のターンのしやすさといったら、Hart FreeLaunchの比ですらなく、瞬時の180°ターンなども簡単である(私は上手くないが)。
今回はインラインスケートにおける瞬時の180°ターンの力学について考察を行ってみたい。瞬時の180°ターンに必要なことは以下のようなものである。まず、前向きに進んでいる状態から瞬時に後ろ向きになって進む場合を考えてみる。状態の変化は以下のようなものだろう。
- 前向きに進んでいる。
- スケートを瞬時に回転させる。
- スケートが180°回転した、すなわち、反転したところでスケートの回転を停止させる。
- そのまま、後ろ向きになった状態で進行する。
- 前向きに進んでいる。
- スケートブーツの爪先で立つ。
- スケートブーツが勝手に180°回転し、反転したところでスケートブーツの回転が勝手に止まる。
- いつのまにか、後ろ向きになった状態で進行している。
まずは、足を回転させてみると、その回転軸は下の図で紫の円で示したような場所に位置することがわかる。土踏まずと中指の根元の中央辺りである。
 誰がなんと言おうとこれは「足」 |
この図を「インラインスケートのブーツを履いた場合」で示したものを以下に示す。
 |  |
それでは、つま先で立ってみよう。どういうものに近似できるだろうか?
 |  |
何か見覚えがないだろうか? そう、台車の足部分である。ここまでくると判りやすい。台車の場合で考えれば、良く実感できる筈である。
 |  |
それでは、簡単な力学計算をしてみる。「足の回転軸」と「地面に接触しているローラ部分」を拘束系の剛体問題と考えてみよう。インラインスケートのローラは「足の回転軸」と「地面に接触しているローラ部分」を結ぶ方向にはいくらでも回転できる。したがって、転がり摩擦を無視すれば、その方向に関しては「地面に接触しているローラ部分」は地面からは何の力も受けない。しかし、ローラは「足の回転軸」と「地面に接触しているローラ部分」を結ぶ方向と直行する方向には回転することができない。したがって、その方向へ地面から力を受けることになる。滑っている人の速度をVとすれば、「地面に接触しているローラ部分」が「足の回転軸」と「地面に接触しているローラ部分」を結ぶ方向と直行する方向に受ける力はVsinθである(シータは文字化けしそう...)。
 |
もうここまでくれば、一目瞭然である。「インラインスケートを回転させる力」であるVsinθ(シータは文字化けしそう...)をグラフにすると以下のようになる。ここで、θ(シータは文字化けしそう...)がPiを過ぎたところで、-Vsinθ(シータは文字化けしそう...)になっていることに注意してもらいたい。
 |
このグラフは縦軸が任意単位の「インラインスケートを回転させる力」を示しており、横軸がインラインスケートの回転軸に対する角度である。ちょっとでも、インラインスケートが回転軸に対して傾くと(θ(シータは文字化けしそう...)=0でなくなると)つま先を後ろへ向かせる方向へ力が働き急激に回転する。そして、つま先が真後ろを向き始めるとその力は弱くなる。つま先が真後ろを向いたところで、その力は0になり、もし回転しすぎると、また、真後ろへ戻す力が働く。そなわち、つま先が真後ろへ向いているのが非常に安定なわけである。
というわけで、インラインスケートで前進中に爪先立ちすると、何も考えなくてもちょうど180°回転してくれるというわけである。もちろん、後ろへ進んでいるときに回転したいならば、進行方向側のかかとで立てば良いわけである。
今回の話はひとまずこんなところである。
1999-11-23[n年前へ]
■ミニスカートの幾何学 
32cmの攻防戦
早朝、東名高速で事故渋滞にはまってしまった。仕方がないので、TVを眺めていると、面白い話をやっていた。それは、ミニスカートの丈の話である。何でも、最近の流行はミニスカートの丈が32cmのものであるらしい。女子高生?などが言うには、
「34cmだと長いしぃ。」だから、32cmだと言うのだ。別に、オリンピック選手でもないのだから、ミニスカートの丈の限界まで挑戦しなくても良いだろう、と私などは思ってしまう。しかし、彼女たちはそう考えないらしい。人それぞれである。
「30cmだと下着が見えちゃうしぃ。」
それにしても、スカートの丈が32cmと30cmの間でそんなに、違いがあるものだろうか? 「見える・見えない」を決める分水嶺がその2cmの違いにあるものなのだろうか? 妙に不思議である。 そこで、ミニスカートの幾何学について考えてみることにした。題して「32cmの攻防戦」である。
何より先に確認しておくが、私は今回は科学的好奇心で動いているのである。そこに、一点の不純な気持ちも存在しないことを、ここで確認しておく。いや、むしろ、女性のためのミニスカート理論の構築を目指しているといっても良いかもしれない。といっても、信用されないとは思うのであるが...
 |
さて、先のTV番組によれば、腰からスカートの先までの長さを「スカートの丈」というらしい。また、先のTV番組により、「腰から下着の一番下の部分(股下を計るときの一番上)までの長さが大体25cmである」という重要な情報を得ることができた。
それでは、解析を始めてみよう。以下に、今回考えた「ミニスカートの幾何学」を示す。なお、今回使用する長さの単位は全て(cm )である。
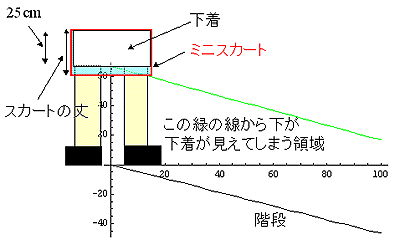 |
まず、階段の途中に立つミニスカートを履いた女性の下着中央部分とミニスカートの最下部を結ぶ直線を考える。この線よりも下が、下着が見えてしまう領域である。もちろん、階段の下には潜り込めないわけであるから、その線と階段で囲まれた領域内から見た際に下着が見えてしまうわけだ。その線のことを「下着防御ライン」と呼ぶことにする。
さて、ミニスカートの形状を考えよう、スカートの丈はもちろん入力条件としてわかる。すると、足りないパラメータは幅である。そこで、ヒップ周りが88cmとしてスカート中央から端までの長さ(rcm)を求める。2πrが88cmであるから、
r = 14cmとなる。
また、駅などの階段というと25度位だろうか。30度というとかなり急な階段である。湘南通商の階段とか急な階段は色々あるが、今回は急な階段の斜度として、25-30度位としておく。ちなみに、京都駅北口のエスカレータで実測したところ、25,6度であった。
それでは、スカートの丈が32cmで階段の角度が30度である場合の計算をしてみる。女性の股下は仮に70cmであるとしておく。おそらく、身長160cm位であれば、この程度であろう。
それでは、ミニスカートの丈が32cm、30cmの時の「下着防御ライン」を計算したものを示す。
 |  |
緑、すなわち、ミニスカートの丈が32cmの時は「下着防御ライン」は階段とほぼ平行である。それに対して、丈が30cmの時の「下着防御ライン」は、ミニスカートを履いた女性から離れるほど階段よりも上に離れていく。ということは、人間の視点位置が「下着防御ライン」を越えるということである。すなわち、下着が見られてしまうということだ。
階段と「下着防御ライン」の差、すなわち、人の目の高さがこの程度ならミニスカートの下の下着を見ることができる、というものを示してみる。
 |
32cmの丈の場合、10m(1000cm)離れても、目の高さが150以下の人しか「下着防御ライン」を突破できない。すなわち、女性は事実上「下着を見られる恐れがない」といって良いだろう。もちろん、20mとか離れたら別である。しかし、超人的な視力がなければ、そのような条件下で下着を確認することはできないであろう。
それに対して、30cmの丈の場合には6m離れた時点ですでに視点が2mの位置にある人でも「下着防御ライン」を突破できてしまう。これでは、「全ての人に下着を見られてしまう」ということになる。
もし、女性の身長が20cm程度高く、180cm程度であったら、どうなるだろうか。おそらく、股下長さは10cm程度長くなる。すると、上の図(階段と「下着防御ライン」の差)の緑、赤ラインは10cm程度高くなる。それでも、緑の32cmスカートの「下着防御ライン」はやはり安全圏といえるだろう。
また同様に、厚底サンダル・ブーツなどを履いた場合には股下長さが20cm弱高くなると考えられる。この影響を考えると、長さとしては身長の影響よりも大きいわけである。それは、身長の1/2が股下長さの増加に繋がるのに対し、厚底靴の長さはそのものずばり股下長さの増加に繋がるからである。しかし、それでもやはり緑の32cmの「下着防御ライン」は安全圏である。
すなわち、32cmと30cmのスカートの丈の長さの間には、「下着が見える・見えない」に関する分水嶺が確かに存在するのだ。先の、
「30cmだと下着が見えちゃうしぃ。」という発言は理論的に裏付けられたのである。
それでは、次に階段の角度が25度である場合の計算をしてみる。
 |
緑の線、すなわちスカートの丈が32cmの場合の「下着防御ライン」が階段にどんどんすり寄っているのがわかると思う。すなわち、「下着防御ライン」はより強固なモノとなっているのである。階段と「下着防御ライン」が女性から離れるほど近づくのである。次に、階段と「下着防御ライン」の差を見てみよう。
 |
緑線、すなわちスカートの丈が32cmの場合に注目する。 女性から、離れても、近づいても、何人たりとも、下着を見ることはできないのだ。下着がシュバルツシルト半径の中に隠されるといっても良い。女性の安全を確保する「完全安全条件」を満たす「下着防御ライン」が完成されているのだ。
これは階段と「下着防御ライン」が平行である条件を境として、そのような条件が達成される。その条件よりより「下着防御ライン」が強固になると、誰も「下着防御ライン」を突破することはできない。すなわち、「完全安全条件」が達成されるのである。
この絶対に下着を防御可能(「完全安全条件」)な「完全安全条件」とは、階段と「下着防御ライン」が平行である条件であるから、ミニスカートの丈(xcm)をパラメータとして、
Tan[階段の角度] = (x-25)/14で計算することができる。ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である。もちろん、極端な安産体型の場合には、その14という値を適当に補正する必要がある。
さて、この条件には女性の身長(股下長さ)は関係しないところが面白い。もちろん、厚底サンダルなどを履いても同じである。もちろん、若干の影響はあるが、あまり影響はない。
さて、今回の「ミニスカートの幾何学」の考察により、判明した結果をまとめてみよう。
ミニスカート内部の下着が「見える・見えない」には
- ミニスカートの丈が30cmと32cmの間に、分水嶺が確かに存在する
- 絶対に下着を防御可能(「完全安全条件」)なミニスカートの丈(x cm)とは、Tan[階段の角度]= (x-25)/14 により決定される
- ここで、14は腰回りの半径(cm)であり、Hip88cmの人の場合である
- 極端な安産体型の場合には、その14という値を適当に補正する必要がある
- 一方、ミニスカートを履いている人の身長はほとんど影響を及ぼさない
- 厚底サンダルの方が身長よりは影響を及ぼすが、それでもほとんど影響はない
ミニスカートを身につける女性の経験に基づく、「30cmだと下着が見えちゃうしぃ。」理論はなかなか正しいことがわかる。経験というものを軽んじてはいけない、という良い?例かもしれない。結果の伴わない理論に価値はない、ということだろうか。
それにしても、厚底ブーツにミニスカートを履いた女性達は、ロールプレイングゲームの主人公達のようだ。色々なアイテムを手に入れ、冒険を続けている主人公達のようである。ほんの少しだけ、うらやましいような気もする。
さて、こういう話題を書くと少し不安がある。もちろん、私もミニスカートを見ると、妙に心が落ち着かないのも確かに事実ではある。しかし、だからといってことさらに興味津々というわけでもない、と思う。多分。ということで、「できるかな?」の女性読者の数が減少しないことを、ただ祈るのみである。
2000-02-06[n年前へ]
■パノラマ写真と画像処理 Pt.1 
パノラマ写真を実感する
「パノラマ」という言葉は何故か大正ロマンを感じさせる。かつて、流行ったパノラマ館や江戸川乱歩の「パノラマ島奇譚」という言葉がそういったものを連想させるのだろう。私も自分で写真の現像・焼き付けをしていた頃は、フィルム一本まるまる使ってベタ焼きでパノラマ写真を撮るのが好きだった。
そういう癖は持ち歩くカメラが「写るんです」と「デジカメ」へ変化した今でも変わらない。例えば、
の時に撮ったこの写真もそうである。 |
そしてまた、次に示す写真もそうだ。これは1999年夏頃の早朝に箱根の湖尻で撮影したものである。360度のパノラマを撮影したものだ。
 |
観光に行った先で撮影したと思われるかもしれないが、残念ながら違う。出勤途中に撮影したものである。豊かな自然がありすぎて、涙が出そうである。
パノラマ写真としては、こういう景色を撮ったものも良いが、人が写っているものも良い。私の勤務先がこの大自然の中に移転してくる前、都会の中にあった頃に居室で撮ったパノラマ写真などはとても面白い。窓の向こうにはビルが見えたり、周りに写っている人ですでに退職した人が何人もいたりして、涙無しには見られない。
もちろん、こういった写真はパノラマ写真で楽しむのも良いが、もっと実感できるものに加工しても楽しい。私がかつて都会の居室で撮影したものは、当時はAppleのQuicktimeVRのムービーファイルに変換して遊んでいた。今はもうない居室の中をグリグリ動かすのはホロ哀しいものがあり、とても味わい深かった。
ところで、WEB上でそういうパノラマのVRファイルを見せるにはどうしたら良いだろうか?もちろん、AppleのQuicktimeVRを用いれば良いわけではあるが、プラグインが必要である。私はQuicktimeは好きであるが、ブラウザーのQuicktimeのプラグインは嫌いである。WEBを眺めているときに、「Quicktimeのアップグレードはいかがでしょう?」というダイアログが出ると、少しムッとしてしまう。そこで、Javaを使うことにした。いや、もちろんJavaをサポートしていないブラウザーもたくさんあるが、こちらの方がまだ好きなのである。
そのようなパノラマのVRを実現するJavaアプレットには、例えば
- Panoramania
- http://www.lamatek.com/lamasoft/Panoramic/test.html
- Javaアプレット(パノラマver1.1)
- http://village.infoweb.ne.jp/~fwbc6098/java/panorama/panorama.htm
- TheVRApplet1.0
- http://www.physik.uni-greifswald.de/~jonas/VRApplet/VRApplet.html
- how toinsert the panorama show (java applet) inside your home page ?
- http://persoweb.francenet.fr/~carl/brique/exapano1.htm
さて、ここまでは単なる前振りである。本題は、実はこれから始まる。先日このようなメールを頂いた。
私はWindowsを使っているのですが、AppleのQuicktimeVRに興味があって、QuicktimeVRのパノラマ・ムービーを作っています。しかし、素材となる画像の作成に四苦八苦しております。ご承知の通り、
- ライカ版カメラに24ミリ広角レンズをつけて、
- 三脚にパノラマヘッドをつけて、ぐるりと周囲を12枚撮りして、
- 現像、プリントし、
- スキャニングして、ステッチャソフトでレンダリングし、
- それをMacintosh上でMake-QTVR-Panoramaにドロップして、
- 8ミリビデオに広角レンズを付け、
- 90度横倒しにして、10秒程度で1回転するようにステッピングモーターで駆動するパノラマヘッド(自作)に乗せ、
- 高速シャッター撮影し、
- マックのAV機能で円周12枚の静止画を取り出
- し、
- 8ミリビデオを横倒しにして、
- モーター回転するヘッドでぐるりと360度撮影し、
- その撮影した動画ファイルの、各フレームから走査線にして数本分を抽出し(インターレースで256本のうちセンター128本目の前後数本の走査線分)、
- それを貯めて1枚のjpgファイルにする、
- そのJPEG画像をMakeQTVRPanoramaの入力にして、パノラマムービーを作る、
その場合には、スリットスキャンカメラを入手し、それをカラープリントする設備を準備すればいいのでしょうけど、高価です。
そこで、
長々と分かりにくいことを書きましたが、要は、「マックで動く電子スリットスキャンソフト」をなんとか作っていただけないでしょうか?もし、そのようなソフトがあれば、
まずは、答えを先に書いてしまおう。私が作らなくても、
- NIH-Image (MacOS)
- ScionImagePC (Windows)
- 複数画像(動画)からの走査線抽出
ScionImagePCの動作画面を以下に示す。NIH-Imageとほぼ同じである。
 |
これらのソフトのStack-Slice機能を用いれば「複数画像(動画)からの走査線抽出」ができる。その使用例と、その面白い座標軸変換について考えてみたい。しかし、このページは少々重くなってきた。まして、走査線の抽出の話は使用画像が多くならざるをえない。そこで、次回、詳しく使用例を紹介することにする。よく、次回といったまま数ヶ月経つことがあるが、今回は大丈夫である。少なくとも数日後には登場することと思う(多分)。
あれっ、ここまで書いてからinfoseekで検索すると、
- パノラマ写真のひっみっつっ!
- http://www.imagica.com/nomad/sig98/hitachi/