2000-07-18[n年前へ]
■モザイクの向こう 
隠しているから良いのです
「できるかな?」への質問?で、同じような内容のメールを頂くことがよくある。その内の一つは、
感温液晶の入手先を教えて下さい。というものである。何か不思議な気がするのだが、けっこう感温液晶を欲しいと思う人がいるらしい。しかも、そのような人はインテリア関係を扱う人が多い。「人のぬくもり」を感じさせるものを作りたい、というわけのである。これを逆に言えば、「人のぬくもり」を感じさせないものが世の中には溢れているということなのだろう。液晶という実に物理的なものを通して「人のぬくもり」を感じることができる、ということが実に不思議で同時に爽快でもある。
さて、私自身は新宿の東急ハンズで感温液晶を購入したのだが、その人達のメールによれば、最近はどうも置いていないらしい。仕方がないので、
- 日本書籍 後藤富治 村上 聡 著 おもしろ科学モノ情報 200選 2000年版
感温液晶シートですが、実験材料でなくて遊ぶのにという返事を最近は出すことにしている。
使うのでしたら、光洋 03-3212-1571にあるようです。
日比谷パークビル9F
平日8:30-5:30
JR有楽町駅近く
 |
そういうわけで、こちらの感温液晶の入手方法に関するメールの方は良いのだが、もうひとつのよく頂くメールの内容がある。こちらの方はメールを頂いても、返事ができるわけでもなく、いつもそのままになっていた。その内容はと言えば、
画像処理と言えば、まずはAVのモザイクの消し方を研究して下さい。というものである。AVのモザイクというと、あの映してはマズイ部分を隠すアノ画像処理のことだろう。本来のモザイクという言葉のモノだけではなくて、アノマズイ部分を隠す画像処理一般について、それをどうにかして欲しい、と言っているのだろうと思う。
しかし、そう言われても困ってしまう。もちろん、私は「見えないもの」を「見える」ようにするのは大好きであるし、趣味でも仕事でも、「見える?見えない?」の境界線に興味を惹かれ、日夜考え続けている。だから、AVのモザイク〜マズイ部分を隠すアノ画像処理〜のようにわざわざ「見えない」ように細工をされてしまうと、それを何とか「見える」ようにしたいという気持ちが無い、と言ってしまうと嘘になるだろう。
しかし、残念ながら、このAVのモザイクの件に関しては「見えない」方が良いと思っているのである。それは、私の好みの根幹に関わる部分なのであるが、ダラダラと言い訳を書いても仕方がない、やはりここはFAQに対しての答えを用意しておくべきだと考えて、ここに簡単な説明を書いておくことにした次第である。
まずは、代表的なマズイ部分を隠すアノ画像処理の種類を示してみたい。次に示す画像は左から、
- オリジナル
- オリジナルに「モザイク」をかけたもの
- オリジナルに「ぼかし」をかけたもの
- オリジナルに「塗りつぶし」をかけたもの
 |  |  |  |
この3つのマズイ部分を隠すアノ画像処理のなかから、今回は
- オリジナルに「モザイク」をかけたもの
- オリジナルに「ぼかし」をかけたもの
さて、まずは「モザイク」に挑戦してみたい。試しに、ミロのヴィーナスのヌード画像に対して、「モザイク」をかけてみよう。次に示すのが、とあるヌード画像に対して「モザイク」をかけたものである。
19kB  | 1kB  |
GIF画像ということで圧縮もかけてあるため、一概に比較はできないが、オリジナル画像が19kBであるのに対して、右の「モザイク」画像は1kBしかない。つまり、情報量がおよそ1/20であるわけだ。それもそのはず、上の「モザイク」画像は実はオリジナル画像を単に縮小したものを拡大表示してみたものである。情報量が少なくなるのも当然だろう。
19kB | 縮小したもの(GIF画像) 1kB | 単に拡大表示したもの 1kB |
それでは、画像の情報量が減ってしまっている場合に、元の画像を復元することはできないのだろうか？いや、ハッキリと言えばヌード画像に対して「モザイク」がかけられてしまったとしたら、その「モザイク」の向こうのヌード画像を拝むことはできないのだろうか？
それが実はできるのである。その証拠に巷には「AVモザイク消し器」というものが溢れている。また、そんな大層な機械でなくても、巷には「モザイク」の向こうを見通すノウハウという秘伝が伝えられている。例えば、私がリサーチした限りでは、
- TVの前に半透明のシートを張る
- 目を薄開きにして、TV画面を見る
その原理とは「オリジナルの画像の性質を考える」ことである。先のオリジナルのヌード画像をじっくり見ればわかると思うが、ヌード画像というものは割合滑らかである。マッチョなヌード画像ならばいざしらず、少なくとも女性のヌード画像は普通滑らかな画像であるわけだ。当然である。だとしたら、その性質をフル活用してやれば、「モザイク」の向こうのヌード画像を拝むことができるのである。
もう少しわかりやすく言うと、こんな感じだ。まずは、滑らかなグレイスケールの画像に「モザイク」をかけてみよう。
| オリジナル |  |
| 上の画像に「モザイク」をかけたもの |  |
すると、元のオリジナル画像は極めて滑らかな画像であるのに、下の「モザイク」をかけた画像は「モザイク」のせいで滑らかでなくなってしまっている。だとすれば、「モザイク」画像を滑らかにしてやれば、元のオリジナル画像っぽくなるのではないだろうか？周囲の画像を考えながら、滑らかな画像にすれば良いのではないだろうか？具体的に言えば、注目画素の周囲で平均値などを計算してやればよいのだろう。つまり、「ボカシ」をかけてやれば良いのである。「ボカシ」をかけると画像はソフトで滑らかになる。「モザイク」をかけた画像が滑らかでなくなってしまっているのを、「ボカシ」をかけることで滑らかにして、元の画像っぽくしてやれば良いのだ。
先の秘伝
- TVの前に半透明のシートを張る
- 目を薄開きにして、TV画面を見る
例えば、上の「モザイク」画像にぼかしをかけたものを次に示してみよう。「モザイク」画像にぼかしをかけることで、元のオリジナル画像に極めて近い画像になっていることがわかると思う。
| オリジナル |  |
| 上の画像にモザイクをかけたもの | |
| モザイク画像にぼかしをかけたもの |  |
これが、いわゆるひとつの「モザイク」の向こうのヌード画像を拝む秘訣なのである。試しに、先のとあるヌード画像に対して「モザイク」をかけた画像を「ぼかす」ことで「モザイク」の向こうのヌード画像を拝んでみたのが次の画像である。「モザイク」画像よりはオリジナル画像っぽいことがわかると思う。
| オリジナル | オリジナル画像に モザイクをかけたもの | モザイク画像に ぼかしをかけたもの |
 |  |  |
さて、それでは逆にオリジナルに「ぼかし」をかけることでマズイ部分を隠すアノ画像処理をした場合はどうだろうか？この場合は「モザイク」の向こうのヌード画像を拝むことはできるだろうか？
といっても、こちらは以前
で扱っているので、ここでは詳しく書かない。ぼけた画像は例えば、- ウィーナ・フィルタ
- ハイパス・フィルタ
と書くだけでも何なので、試しに、Photoshopのカスタムフィルタで簡単な「ボカシ復元用フィルタ」を作成してみたものをここにおいておく。Photoshopユーザは試してみると面白いかもしれない。
このカスタムフィルタの内容はごく簡単なオペレータ演算で、次の図に示すようなオペレータ演算子を用いたフィルタである。 |
試しにこのカスタムフィルタを用いて、とあるヌード画像に対してかけられた「ぼかし」画像の向こうのヌード画像を拝んでみたのが次の例である。ちなみにここでの「ぼかし」はPhotoshopでガウス「ぼかし」の半径4ピクセルの設定でフィルタをかけてみたものだ。
| オリジナル | オリジナル画像に ぼかしをかけたもの | ぼかし画像に 先のカスタムフィルタをかけたもの |
 |  |  |
こんな簡単なカスタムフィルタでもとあるヌード画像の「ボカシ画像」を鮮鋭化できて、その「ぼかし」の向こうのヌード画像を拝むことができることが判ると思う。
実際に、私がネット上で膨大な数のエロ画像、いや違った「ボカシ」画像だ、を収集し試した結果ではかなりの割合の画像に対して、驚くべき効果を挙げることができた。本WEBに訪れるような方のほとんどには当然の知識だとは思うが、もしもこういった処理をかけたことのない方がいらっしゃれば、是非一回挑戦しみてもらいたい。特に素人ヌードの「ぼかし」画像がお薦めである(あくまで復元効果の大きさに関してだけど)。
さて、ここまで書いてから言うのはどうかと思うのだが、以前
でも書いたように、私は「素晴らしい芸術は完全な自由の中では生まれない」と思っている。それと同じで、制限の中で表現する方が実は素晴らしいものができると思っているのである。それは、私服の女子高生には心ときめかないが、制服の女子高生には思わず目を惹かれるのと同じである。完全に何でもありの私服だと実はそう簡単に輝かないのだが、制限のかかっている制服だと何故かとても輝いてしまうのと同じだ。私などは、通っていた高校が制服がなかったため、思わず同級生に「セーラー服を着て来てくれぇ」とリクエストをしてしまったくらいである。あれ、何の話だっけ...そう、つまりわざわざ隠してある部分を眺めてみることは良いとは思わないのである。隠してあるものは、隠しておいたままにしておいた方が良いのではないか、と思うのである。
そう言えば、先ほど「ミロのヴィーナス」の画像用に表紙を使わせて頂いた細野不二彦のギャラリーフェイクの中では、主人公藤田が、
「ミロのヴィーナスは腕が隠されているからこそ、人々の心を捉えたんじゃないですかね」というようなことを言う。私も本当にそう思う。
 |
「ミロのヴィーナス」の存在しない腕を想像することで、現実には作りえない理想の姿を、その像を見る人々は感じることができるのだろう。隠してあるからこそ、良いのである。
あまりに緻密に描写した弟子に「言い仰せて何がある」と言ったのは松尾芭蕉だったはずだ。想像する余地を残して、現実よりもさらに大きいものを表現した方が良い、ということである。私も本当にその通りだと思う。ある一部分だけを切り取ってその部分だけを見てみて、後は想像力におまかせというのが、私も表現としては一番良いと思うのである。もちろん、全ての人の想像力を越えるものを表現する力があるというならばともかく、そんなことができないのならばわざと一部分だけを表現するのが一番良いと思うのである。
いや、だからって別に私が変な想像をしまくりってわけじゃないとは思うけど。かといって、私が想像力とか好奇心が少ない方かと言われると...うーん...
2002-02-20[n年前へ]
■「やおい」の評価演算子
ベクトルの彼方で待ってて II
東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか？
「福田Ｘ小泉っていうのは、結構上手くやっているのかな？」と私が言うと、おもむろに
「あれは、福田Ｘ小泉じゃなくて、絶対あれは小泉Ｘ福田なのー」とその記者が言ったのである。何を言っているのかその意味がよく判らないまま、「ん〜？」と私が首を傾げていると、繰り返し
「福田Ｘ小泉と小泉Ｘ福田は全然意味が違うのー」と言い始めるのである。何が何だか訳がわからない。じゃぁ、何か？小泉Ｘ福田だと小泉純一郎が総理大臣で福田康夫が官房長官だけど、福田Ｘ小泉だと福田康夫が総理大臣で小泉純一郎が官房長官になるとでも言うのか？？政治の世界では、言う順番で総理大臣が決まるとでも言うのか？と私が口をはさむと、
「そう。ただ、ちょっと政治の世界とは違う世界かも〜。政界じゃなくて、やおい界ではー。」と言うのだ。なんだコイツ？政界は判るけど、やおい界って一体何処の世界の話だ？？と、困惑する私も構わず、そこから延々と長い演説が始まった…。その大河ドラマのようにやたらと長い話を要約すると、
- やおい → 一部の女性が好む「男性同士の恋愛もののストーリー」のこと
- Ｘ → やおいの世界で恋愛の関係を示す記号。例えば、AさんとBさんが恋に落ちるであれば、Aさん×Bさんと表す。で、ここで重要なのは先に位置する方が「攻め役」となって、後に位置する方が「受け役」となる…。つまり、例えばサド侯爵とレオパルド・マゾッホであれば攻め役がサド侯爵で、受け役がマゾッホなので、サド×マゾなのである。決して、マゾ×サドではない…
で、日本酒を飲みながら、まだまだ続くその話に悪酔いしていると、「カップルの順序が重要なんだー」という言葉を聞いて、ふと中学の頃の数学の授業を思い出した。その頃、大学を出てまだ一年目の斉藤慶子似の数学の先生と話していたときに、「Hくん、あのね掛け合わせる順序が違うと結果も違っちゃう計算もあるのよ」と教わったことがあった。そんな言葉から私は未知の「数学の世界」をかいま見たりしたのである。 今考えてみれば、新任の斉藤慶子似の女性教師の個人授業なのだから、行列・ベクトルの掛け算の順序なんかじゃなくて、「もっと違う順序」を手取り足取り教えてくれても良かったんじゃないか、とか思ったりするし、そうすれば、私は未だ見ぬ「大人の世界」を覗き見ることができたのではないか、と思ったりもするのだけれど、そんなことは残念ながら無くて、私はただ「行列・ベクトルの世界」を覗いただけだったのである。
で、そんな昔話を思い出したせいか、頭の中でこんな風に思ったのである。そういえば、これまで「できるかな?」では数多く「恋の力学」でも遊んできた。ただ、そこでは「惹かれ合う恋心の大きさ」だけに注目して、そのカップルの中での役割などは考えたことがなかった。そこで、今回は「やおい」のカップルの「役割・順序」に注目し、その「役割・順序」を評価する演算子を行列・ベクトルの掛け算になぞらえながら考えてみることで、これまでと同じく色々な「恋の形」を眺めてみたいと思う。
まずは、色々な人物（実際の人物であったり、小説などの登場人物であったり）のタイプを二次元空間に配置しよう。「この人は結構攻め役が合いそう」とか「この人は絶対受け役が合うのだー」という適性を
- 攻めベクトル
- 受けベクトル
 |
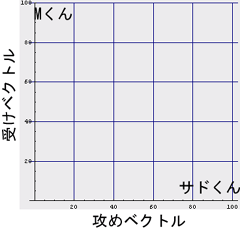そして、カップリング適性では「A×B、B×Aが全然違う」ということから、外積(ベクトル積)をそのまま流用して、適当な評価関数を作ってみるのが自然だろう。まず、
カップリング適性ベクトル = （攻め度(s)、受け度(m)）と表記して、例えばAさんのカップリング適性ベクトルを(As, Am)と表すことにしてみよう。すると、Aさんが「攻め」でBさんが「受け」のカップリング適性は、この二人の適性ベクトルのベクトル積として表すことができる。つまり、
A×Bのカップリング適性 = ( As * Bm - Am * Bs )となるわけである。式を眺めれば判るように、Aさんの攻め度が高くて、Bさんの受け度が高ければ、この評価関数は高い値を返す。つまり、「A×Bの順序は正しいのだー」という評価を返す。つまり、「A×B」はなかなか良いカップルだー、と教えてくれる。また、もしAさんの受け度が高くて、Bさんの攻め度が高ければ、低い値を返す。つまり、「A×Bの順序は絶対間違ってるのだー」と評価してくれるのである。なんともありがたいことに（いや別にありがたくはないか…）、この「やおいのカップリング評価演算子」が「福田Ｘ小泉」と「小泉Ｘ福田」のどちらが自然なのかを教えてくれるのだ。試しに、上のサドくんとMくんであれば、「サドくん×Mくん」= (100,0)×(0,100) = 100*100 - 0*0 = 10000でとっても「良い感じ」でああるが、「Mくん×サドくん」= (0,100)×(100,0) = 0*0 - 100*100 = -10000で「このカップリングは絶対順序が違うー」と判るわけである。
= Aさんの攻め度 * Bさんの受け度
- Aさんの受け度 * Bさんの攻め度
とりあえず、今回はこの評価演算子を作成するところまでで終えたいと思うが、いずれこの「やおいの評価演算子」を武器にして、いつか（?）「やおいの世界= やおい界」に限らず、色んな数多くの恋の関係を目に見えるようにしてみたいと思う。そして、これまで数多く考えてきた「恋の〜シリーズ」を充実させていきたいと思うのである。
ところで、今回のカップリング適性評価演算子は基本的に外積そのものである。つまり、この演算が返す値は「二人のベクトルでできる平行四辺形の面積」に等しい。つまりは、「二人のベクトルでどれだけ色んな違うことがきでるか」を示す尺度である。そして、その値は二人のベクトルが直交する時、すなわち二人のベクトルが重ならず独立である時に最大値となる。つまりは、「二人のベクトルが違えば違うほど大きく」なる。例えば、先の「サドくん×Mくん」であれば二人のS,M趣向が完全に正反対であったからとてもお似合いのカップルになったのである。
これをいわゆる恋の話で考えてみると、とっても独立な二人、趣味が重ならない二人がお似合いだということになる。なるほど、そんなカップルも世の中にはたくさんいることだろう。そんな人達を「外積タイプのカップル」と呼ぶことができると思う。
一方、趣味が重ならないカップルだけでなくて、世の中にはそれとは正反対の「趣味が重なる良いカップル」も数多くいる。それは「内積タイプのカップル」である。内積はA,Bベクトル間の正射影に比例する量であって、つまりは「二人の重なるベクトルの大きさ」である。それは例えば、相手の中に自分を重ね合わせるような「二人の重なる部分が二人を結びつけるようなカップル」なのである。
「理系と文系」・「男と女」が対極的なものでも、相反するものでもないのと同じく、「外積カップルと内積カップル」も別に二つに分けられるようなものではないだろう。「外積タイプの恋」も「内積タイプの恋」が混じり合って、それぞれに良いところもあれば、危ういところもあって、などと想像してみるのも面白いに違いない。そして、さらにはもしかしたらベクトル空間で萌えることができるようになったりするかもしれない。
そういえば、ふと考えてみると以前「恋の形を見た人は」で最後に引用した本橋馨子の「兼次おじ様シリーズ」は男性同士の恋の話だった。つまりは「やおい」の話だった。そこで、もう一度そのセリフを最後に飾って眺めてみようと思うのである。
「愛はどんな形をしているか知っているか？」「見た事ないからわかりません。」「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...
もし愛に優劣を決めるものがあればなんだろう？... 異性愛か、同性愛か、そんなものじゃない …たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」
2002-12-01[n年前へ]
■ATOK数式処理プラグイン「AtokMathParser」
ひとまず、できた。変数への代入処理なんかもできたら便利そうなので、それはいつかのバージョンアップ時に実装する予定。また、方程式を解く機能なども実装する予定…。高機能な数式処理システムMuPadと連携するバージョンなども面白そうだけれど、そこまでやると逆にあまり便利じゃないかも。というわけで、今日作った「ATOK用数式処理プラグイン(全角→半角変換ミス修正版)」を置いておきます。一番最初のバージョンでは全角→半角変換ミスがありましたので、半角時に"="が有効でなくなる人は修正版をご使用下さい。また、自分のPCでしかテストしていないので、ぜひフィードバックを下さい。そもそも、他のPCで動くかどうかもパッケージなどの兼ね合いもあって不安ですから。
さて、このソフトはATOKで入力中の数式の計算結果を変換表示するプラグインです。ATOKユーザーで電卓を使うような機会のある人であれば必須のツールになるかもしれません。とりあえず、かなり便利だと思います。
インストールはアプリケーションを適当な場所に移動後（その後移動しないこと）、起動して「インストール」をクリック。アンインストール時は「アンインストール」をクリックです。Windows2000ならその後ログオフすれば、その他では多分再起動すれば使えるようになります。
全角→半角変換も入っていますので、「３／２＊１２」なんて入力しても良いですし、"sin(pi)*12/log(12)"なんて半角で入力しても良いです。使える関数や演算子も「結構多いです」から、とりあえずちゃんとしたドキュメントを書くまで適当に色々と試して下さいな。
ちなみに、入力の最後に"="を付けると、入力した内容も変換結果に表示されます。例えば、「３／２＊１２＝」と入力して変換すると"3/2*12= 18"となります。
また、AMETを使用するときにはショートカットを駆使することになると思いますが、多分デフォルトでは「Shift+Ctrl+F10 → 2」になると思われます。また、Ctrl+F9→Eで半角英字入力になりますし、Ctrl+F9→Hで全角かな入力になります。"sin"とか"log10"とか半角英字入力が必要な際にはショートカットで切り替えましょう。多分、ATOKのプロパティ設定から一発ショートカットでも設定しておくときっと便利になるんでしょう。
ところで、結局Input Calc for AMETは私は上手く動かせなかったので、それとの比較は判りません。また、ATOKのバージョン違いなどの対応もよく判りません。とりあえず、AmetDateの資料・ソースに感謝なのです。
2002-12-02[n年前へ]
■演算子・関数一覧
ATOK数式処理プラグインの使用可能な演算子・関数一覧を置いておきます。ATOKで演算子・関数が使えるなんていいと思いません？
2004-03-30[n年前へ]
■超萌え代数 - hyper-moe algebra -
「初等ロリータ指向（×嗜好）プログラミング」「ロリータ指向プログラミング中級基本編」を開発したEntis Lab.が今度は数学を生み出した。その数学の名は「超萌え代数-hyper-moe algebra- 」 萌えもついにhyperになったのである。
「萌え」の世界の原点（萌え零点）とは一体何処か？、「萌え」は果たして可換なのか？、そしてはたまた、さらに一般化された「超萌え-hyper-moe algebra-」とは何なのか？かつて、「やおい」の評価演算子で「やおい代数学」が生まれたように、「萌え」も数学としてその姿が明らかになる、…のかも…。
」など。