1998-11-22[n年前へ]
■OHPによるモアレと光の干渉の相似について考える。 
ヒラックス・ディザの提案
「位相保存ディザマトリックス」
まず初めに、4 x 1ドットからなる基本マトリックスを考える。その各ドットは白か黒の値を持つ。例えば、このような感じである。 |
この「黒、黒、白、白」というパターンを次の図と見比べる。
 |
 |
「モアレのデバイス依存について考える。」で行ったようにこのようなパターンをOHPで打ち出し、重ね合わせてみる。例えば、位相0と位相180のものを重ね合わせたらどうなるだろうか。4x1ドットのマトリックスの全てが黒になる。すなわち、真っ黒になるのがわかるだろう。それでは、位相0と位相90のものではどうだろうか。4x1ドットのマトリックスの内、3ドットが黒、1ドットが白である。位相が同じものどうしを重ね合わせると、元と同じく、2ドットが黒、2ドットが白である。
ということは、「位相が同じ物どうしであれば、元の明るさを保持する」、「位相が逆であれば真っ黒になる」、「位相が少しずれているのあれば、明るさはその分少し暗くなる」という性質があることがわかる。光の干渉の場合とほとんど同じ性質を持っているのがわかると思う。違うのは、同じ位相のものどうしが重ね合わさった時に、重ね合わせた分明るさが2倍になるか、そうでなくてそのままなのかという違いだけである。
つまり、この4x1ドットのマトリックスは「きちんと演算が成立する位相情報が記録されている」ということになる。そして、位相が異なるものを重ね合わせた時の位相情報の保存までも考えてやるならば、先ほどの例1は次のように位相の定義を変えてやるほうがいいと思う。
 |
この例2では位相の数字は各矩形波の中心位置を現すことにしている。それでは、この定義を用いて、位相90,180のものを足しあわせたらどうなるだろうか。下に示すのがその結果である。
 |
位相90と位相180のものを足しあわせると、波形はブロードになり、中心すなわち位相135のものができているのがわかる。また、明るさはこれまでが、2/4だったものが1/4であることになり、強度も弱まっているのが表現されている。
つまり、このようなマトリックスによる表現は波の持つ位相と強度と波形を表現し、演算も成り立っていることがわかる。それでは、例2の基本マトリックスが縦方向に繰り返されている画像(1(基本マトリックス)x8ピクセル)を考える。こんな感じである。
  |
これは下方向から進行している矩形波の様子そのままである。なお、この図でも基本となるマトリックスは4x1ドットであるから、この例では要素としては1x8ピクセルを示しているのである。どの要素も振幅(強度)自体は同じである。平均の明るさは同じである、と言い換えても良い。また、波形自体も同じである。しかし、位相が異なっている。波の進行そのままである。
さらに強度情報を加える
このような白、黒のみの2値表現(といってもこの表現にはモアレが欠かせず、そのためには2値表現がふさわしい)では、波の位相、波形、強度を独立に変化させることはできない。例えば、波の波形を変えると強度も変わってしまう。それを独立にしてやろうと思ったら、階調を増やしてやれば良い。しかし、2値表現のままという制限付きであるから、面積階調を使うことになる。これまで4x1ドットのマトリックスで表現していたものを、例えば、4x4ドットのマトリックスにしてやればよい。以下にその例を示す。例Aの強度が例Bの1/4であることがわかるだろう。 |
 |
このような「位相、波形、強度情報を保存し、演算も成立する」マトリックス表現を仮に「HiraxDither(ヒラックス・ディザ)」と呼ぼう。先の「モアレのデバイス依存について考える。」で使ったスペックルパターンの例はこのヒラックス・ディザの簡易なもの(2x1基本マトリックスのもの)を使っていた。
また、「モアレのデバイス依存について考える。」で使った同心円状の画像のモアレのパターンは実はヒラックスパターンの特殊な例(1x1基本マトリックスのもの)を用いていたのである。そこでは、単に位相情報しか記憶されていない。この場合には、白、黒が位相情報を現していたのである。だから、黒、黒どうしの所(すなわち、位相が同じ所)では平均の明るさは変化せず、黒、白が重なった部分(すなわち、位相が反対である所)でのみ打ち消し合い、暗くなっていたわけである。波形も、強度情報もこの場合には記録されていない。
「ヒラックス・ディザ」とホログラフィーの相似点
このようなヒラックス・ディザの「ディザ・パターン内部、すなわち、微視的には位相情報や振幅情報を記録し、巨視的に見ると強度分布のみが認識される。また、相互の演算(干渉)によって違う画像を再生することができる。」という特徴は実によくホログラフィーと似ていることがわかる。 また、もう少し深く考えると、もっと他の分野とも繋がるかもしれない。いずれ、また考えてみたい。
1999-02-28[n年前へ]
■分数階微分に基づく画像特性を考えてみたい 
同じ年齢でも大違い
前回、分数階微分の謎 - 線形代数、分数階微分、シュレディンガー方程式の三題話- で分数階微分について調べた。例えば、0.7階微分といった、整数階でない微分である。今回はそれを使った応用を考えてみたい。
人間の視覚というものは明るいものは強く感じることができる。これは当たり前である。そして、それだけでなく、強さが変化している所にも(興味を)強く感じ取るようになっている。岡本安春氏の「Delphiでエンジョイプログラミング」によれば、そのような考えはLaming(1986)がdifferential coupling(差動結合)として発表しているらしい。
ということは、人間が画像を感じる特性というものは、画像強度と画像強度変化(画像強度の一階微分)の中間的なものであると言うことができるかもしれない。とすれば、分数階微分を導入すれば面白い表現ができるかもしれない。
今回は、そういう考えのもとに分数階微分を用いて人間の画像特性について考えてみたい。
まずは、元画像を示す。元画像はガウス分布に基づいて作成されたものである。
 |  |
まずは、左の元画像を見て欲しい。どこに強い感じを受けるだろうか?白い部分はもちろんであるが、白と黒の境界部にも強い感じを受けるだろう。ギザギザになっているのはデータが少ないからなので、無視して欲しい。というわけで、人間の視覚画像特性は
- 画像強度
- 画像強度変化(画像強度の一階微分)
 元画像 |  |
 1/2階微分画像 |  |
 15/20階微分画像 |  |
 1階微分画像 | 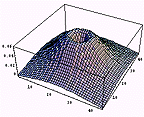 |
白地に黒画像バージョンも示しておく。紙の上の画像に慣れた人にはこちらの方が良いだろう。
 元画像 |
 1/2階微分画像 |
 15/20階微分画像 |
 1階微分画像 |
なお、今回の画像の作成は次のような手順で行っている。
- 1次元のガウス分布を作成する。
- 微分値が正であるような半分の領域を線対称に回転させ、2次元画像を作成する。
今回は
- 画像強度
- 画像強度変化(画像強度の一階微分)
- 電位
- 電界(電位の微分、といっても本来は電位が電界の積分か)
- 人口密度
- 人口密度変化(人口密度の微分)
さて、分数階微分を調べる中で、バナッハ空間についても調べた。調べ始めた時には、聞き覚えもなかったが、調べてみるとヒルベルト空間の導入で登場していた。きれいさっぱり忘れていたようである。
京大数学教室 徳永健一氏のWEB (http://www.kusm.kyoto-u.ac.jp/~kenichi/)
から辿れる「「年齢の本」数学者版」によれば
バナッハがバナッハ空間を提唱したのは30歳の時であるらしい。(http://www.kusm.kyoto-u.ac.jp/~kenichi/age/30.html)
うーん...
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
 |  |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
 |  |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 |  1階微分 |
 13/10 (=1.3)階微分 |  15/10 (=1.5)階微分 |  17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
2000-01-03[n年前へ]
■音場の定位を見てみたい 
立体音感を考える その2
前回(といっても間に他の話も挟まっているのだが)、
で「音の立体感」について考え始めた。今回はその続きである。「音の立体感」を考えるための道具を作る準備をしてみたい。色々なことを考えるには、その目的にあった測定器が必要である。何か新しいことをしようと思ったら、そのための新しい測定器を作成しなければならない(と思うだけだが)。そして、何より私は計測器なんてほとんど持っていない。だからといって、計測器を買うお金があるわけではない。というわけで、困ってしまうのだ。
そこで、立体音感を考えるための測定器を作っていくことにした。といっても、すぐにできるとも思えないので、色々実験をしながらボチボチとやってみることにした。勉強がてら、ボチボチやってみるのである。オーディオ関連のことにはかなり疎いので勉強にはちょうど良いだろう。
資料をいくつか眺めてみたが、特に
- 「立体視の不思議を探る」 井上 弘著 オプトロニクス社
- 音像定位の因子
- 両耳差因子 (音響信号)
- 音の強さ(振幅)の差
- 位相の差
- 周波数スペクトル因子
そこで、いきなりだが今回作成した解析ソフト「音場くん一号」のアルゴリズムは以下のようになる。
- PCのサウンド入力から、サンプリング周波数 22.05kHz、Stereo 各チャンネル8bitで取り込みを行う。
- 取り込んだデータを4096点毎にウィンドウ(Hamming or無し)処理をかける。
- 高速フーリエ変換(FFT)を行う
- FFTの結果の実部について、左右のチャンネルの差分を計算する
次に示すのが、「音場くん(仮名)一号」の動作画面である。「音場くん(仮名)一号」の画面構成は、
- 右側->制御部
- 左側->計測データ表示部
- 音声波形データ(赤=左、緑=右)
- 周波数(横軸)vs左右での音圧の差(縦軸)
- 時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)
 (黒字に赤、緑の色構成は変更の予定) |
計測データ表示部の拡大図を下に示す。
- 音声波形データ(赤=左、緑=右)
- 周波数(横軸)vs左右での音圧の差(縦軸)
- 時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)
この表示計の意味を例を挙げて説明したい。例えば、下の画面では左の方に定位している音が鳴ったときの状態を示している。一番上の音声波形データでは緑(右)の波形は小さいのに対して、赤(左)の大きな波形が見えている。
また、真ん中の「周波数(横軸)vs左右での音圧の差(縦軸)」では横軸100(任意単位)程度の高さの辺りで左チャンネルに位置する音が発生しているのがわかる。
また、一番下の「時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)」では時間的に一番最後(横軸で右側)の方の横軸560、縦軸100位の位置に白い(すなわち左チャンネルに定位する)音が発生しているのがわかると思う。
 |
この曲のイントロでは、「ポンッ」という音が高さを変えつつ、左右にパンニング(定位位置を変化させること)する。
一番下の「時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)」を示したグラフ中で白・黄色(左に定位)と青・黒(右に定位)する音が時間的にずれながら現れているのが判ると思う。
このようにして、この「音場くん(仮名)一号」では音の定位状態についての「極めて大雑把な」計測が可能である(保証はしないけど)。「音場くん(仮名)一号」を使った他の例を示してみる。
下は種ともこの「O・HA・YO」の中から「The Morning Dew」のイントロ部を示したものだ。
- 左(白・黄)チャンネル方向に定位するピアノ
- 右(黒・青)チャンネル方向に定位するガットギター
 |
これはまるでオルゴールのピンを見ているようだ。あるいは、シーケンサーや昔の自動演奏ピアノのロール譜のようである。対位法などの効果をこれで確認したくなってしまう。
さて、ここまでの例は楽器も少なく、比較的自然な定位状態であった。しかし、以下に示すような場合には不自然なくらいの「音の壁」状態の場合である。かなり状態が異なる場合だ。
 |
これは、種ともこの「O・HA・YO」の中から「KI・REI」のラストのラストコーラス部を示したものである。人のコーラスが重なり合っていく部分である。色々な高さの声が重なり合っていく様子がわかるだろう。
ところが、このグラフをよくみると、同じ音が時間的に持続しているにも関わらず、時間毎に定位位置が左右で入れ替わっているのがわかる。
これはきっとエフェクターで言うところのコーラスなどをかけたせいだろう(素人判断だけど)。人工的にフィルタ処理をしているためにこのようになるのだろう。こういう結果を見ると、「音場くん(仮名)一号」をプログレ系の音の壁を解析してみたくなる。
さて今回は、音声の定位状態を解析する「音場くん(仮名)一号」を作成し、いくつかの音楽に対して使ってみた。まだまだ「音場くん(仮名)一号」は作成途中である。これから続く立体音感シリーズとともに「音場くん(仮名)」も成長していく予定である。
さて、一番先の画面中に"Re"という選択肢があるのがわかると思う。もちろん、これと対になるのは"Im"である。FFTをかけた結果の"実部"と"虚部"である。"実部"の方が左右の耳の間での音の大きさの違いを示すのに対して、"虚部"の方は左右の耳の間での位相差を示すものだ。つまり、ある周波数の音が左右の耳の間でどのような位相差を示すものか、測定しようとするものである。
左右の耳に対する音の位相差というものは、立体音感を考える上では避けては通れないのだろう。しかし、位相差を処理しようとすると、どうしたらいいものかかなり迷う部分がある。また、今回のようなFFT処理をかけたときに得られる位相を用いて良いものかどうかもよくわからない。というわけで、今回は位相解析処理は後回し、ということにした。
2000-01-08[n年前へ]
■着メロの音響工学 
この着信音は誰のだ!? 立体音感その3
街中で携帯電話の着信音が鳴ると、周辺の人が一斉に自分のポケットを探る光景というのはよく見掛ける。それは、まるで「クイズ・ドレミファドン」のようである。そう「超・イントロクイズ」そのものなのだ。「このイントロはオレのか!?それとも!?」と皆が考えている瞬間である。
着メロのイントロが始まるや否や、腰の携帯電話に手をやる様子は「おまえは荒野のガンマンか!」とツッコみたくなる程である。
特に、私の勤務先などでは全員が同じPHSを持ち歩いているせいか、着信音が聞こえ始めると、みな自分のポケットを探り始める。もちろん、そのPHSの着信音は数種類ある。しかし、1500人程度の従業員がいるわけだから、1500人/ 数種類だけ同じ着信音があるわけだ。仮に15種類あるとしても、
1500(人) / 15(種類数) = 100(人/種類)つまり、自分と全く同じ着信音のPHSを持つ人が100人もいるのだ。世の中には「自分と同じ顔の人が七人いる」というが、職場に同じ着信音の人が100人もいるのである。これでは、着信音が鳴ると同時に多くの人がポケットを探るのも自然だろう。
もちろん、この解決策として、「着信音でなくてバイブレーターを使う」というものがあるわけだが、何故かその解決策は許されないらしい。不思議である。
さて、そもそも、何故自分の着信音を区別できないのだろうか? まず、その辺りから考えてみることにする。
着信音が鳴ったときに、「自分の着信音かどうか判断するための基準」は二つあるだろう。それは、
- 着信音の種類
- 着信音が鳴っている位置
着信音の鳴っている位置 = 自分の携帯電話の位置が成立するかどうか即座に判断できれば、着信音が同じでも「自分の着信音であるか」の判断が可能ということだ。
つまりは、「携帯電話の着信音という音源の定位」という問題を考えれば良いことになる。もし、「着信音の定位」が判れば、自分の携帯電話の着信音か他の人の着信音かどうかなんてことは考えなくて済むのだ。そう、今回は「立体音感」シリーズその3だったのである。
それでは、一体「着信音がどこで鳴っているのか、すなわち、着信音の定位」が判るためには何が必要なのだろうか?
前回、
で「音の立体感に関する因子」について- 音像定位の因子
- 両耳差因子 (音響信号)
- 音の強さ(振幅)の差
- 位相の差
- 周波数スペクトル因子
周波数スペクトル因子というのは、例えば、
の中の記述指を前方で鳴らしてみて下さい。 そしてすこしずつ手を頭の側方に、手と頭の距離を変えないようにして、移動してみて下さい。 音量がわずかに大きくなったこととある特定の中域および広域の音がより強調されることに気が付かれるでしょう。 この実験では、指を鳴らす動作は一定の音量と周波数を発生する音源として用いられたわけです。 耳は同一の音源が前方から来る場合と、側方から来る場合で全く違う音と聞き分け、頭脳にそれを登録します。 側方の音は若干大きく、また耳たぶのせいで高い周波数で聞こえます。にあるようなものである。
音波が人間の頭部を通過してくる間に音波の周波数分布が変化し、その変化具合で音波がやってきた方向を知ることができるというものだ(多分)。もちろん、位相分布も変化するだろうが、ここでは周波数分布しか考えない。
こういう音像定位の因子における「周波数スペクトル因子」を考える時に、もし音源の周波数スペクトルがごく狭いものだったらどうだろうか?つまり、単一の周波数しか含まない音源だったらどうだろうか?周波数スペクトルが変化するといっても、単一のスペクトルしか含んでいないのだから、振幅が変化する効果しかない。周波数スペクトルの分布は何ら変化しない。
ということは、「音像定位の因子における周波数スペクトル因子」が上手く作用しないことになってしまう。(もちろん、実際には非線形な効果が存在するだろうから、多少は周波数スペクトルも変化するとは思うが。)
これと全く同じことはまたしても「物理の散歩道」で触れられている。ロゲルギスト著の岩波新書「第四物理の散歩道」の「不規則なものの効用 三節」である。純音より不規則な音の方が「立体感」を得られるだろう、と書いている。
今回、「携帯電話の着信音の定位」を「着信音のスペクトル分布」という観点から調べてみることにする。携帯電話の着信音がどのような波形であるか、どのような周波数分布を持っているかを調べるのである。果たして、携帯電話の着信音の周波数分布はどうなっているのだろうか?(部品点数を考えれば、ほぼSin波か矩形波なのが当然だろうが...)
まずは手持ちの機種で着信音の波形とスペクトルを見てみることにした。使った機種を以下に示す。
 |
それでは、着信音No4と着メロ「この木何の木」の波形とスペクトログラムを次に示す。それぞれのグラフ中で上は「時間vs周波数分布」を示すスペクトログラムであり、下は「時間vs強度」の波形グラフである。
まずこれが、着信音No.4の波形とスペクトログラムであり、
 |
こちらが、「この木何の木」の波形とスペクトログラムだ。
 |
どちらも周波数分布はそれほどブロードではない。すると、「音像定位の因子における周波数スペクトル因子」を用いた「立体音感」がうまく働かないかもしれない。ただし、着信音No.4に関しては時間的に変化しないが、着メロ「この木何の木」に関しては、当然だが時間的に変化していく。
この違いが果たして、「着信音の音像の定位」の判断を左右するものか、自分の耳で実験することにした。着信音No.4と着メロ「この木何の木」を鳴らした時に、どこから鳴っているように聞こえるか判断してみるのだ。
目をつぶり頭の周囲で着信音を鳴らし、その定位を判断してみた。すると、色々な着信音を聞いてみたがいずれも定位の判断がしづらかった。特に頭の前後の判断がしづらい。それは、着信音No.4と着メロ「この木何の木」でも同様であった。やはり、純音に近いと「音像定位の因子における周波数スペクトル因子」が働きづらいのかもしれない。
そして、着信音No.4と着メロ「この木何の木」だが、むしろ着信音No.4の方が判断をしやすかった。メロディだと音が変わるときに定位が変わるかのような感覚を受けた。そのため、判断をしにくかった。もちろん、これは私だけの感覚かもしれない。その辺りは被験者を増やして実験をしてみたい(再実験をする日が来るかどうかは大いに疑問であるが)。
また、もしかしたら着信音No.4の方が矩形波に近く、純音でないのが良かったのかもしれない。もしかしたら、の話だけれど。
もし、今回使った音を聞いてみたい人がいるならば、
これを聞いてみてもらいたい。ただし、サイズがでかいので要注意だ。あとバックグラウンドがうるさいのはハードディスクとファンの回転音である。困ったものだ。 最近多い「同時発声数が多い着メロ機能」というのも、使って実験すると面白そうだ。しかも、音が分厚いヤツがあると、案外良いモノかもしれないな、とうらやましく思ったりするのである。そして、着信音スピーカーがプアァで歪んでいる機種なんかが、色々な周波数成分を含んでいて、実は「着信音の定位」に関しては良かったりするのかもしれない、と考えたりする。しかし、こちらはチットモうらやましくないのであった。