2000-01-31[n年前へ]
■落ちゆくエレベーターの中…で悩みます? 
無重力の理想と現実(仮)
今日もまた「ちゃろん日記(仮)」を読みに行くと、何とも面白い話があった。
である。この「ちゃろん日記(仮)」は「疑問とそこに隠れている真実を見つけだす感覚」に満ち溢れている、と私は思うのである。面白すぎである。さて、今回の話は、エンパイアステートビルでエレベーターが落ちたっていうけど、落ちていくエレベーターの中の人は
- 床に張り付く
- 天井に張り付く
- 宙に浮かぶ
「ほんとう〜にそうか? ほんとう〜にそうか?」
こういういかにも教科書に載っていそうな話には、時として落とし穴がある。教科書に書いてあるのは理想的で単純化した場合の結果である。それを鵜呑みにすると間違えてしまうことになる。極端に言えば、教科書に書いてあるような理想的な状態はほとんど存在しないので、教科書に書いてあるような現象はそうそう再現しない、ということになる。
ピサの斜塔から「落下の実験」を行ったのはガリレオ・ガリレイであると思っていると間違いである、というのは少し違う例になってしまうか。
久しぶりに思い出したが、私の所属していた研究室では重力測定は大きな柱であった。そして、確か大学院の入試問題の内の一題は、まさに
「落ちていくエレベーターの中の人達に働く力を精密に論ぜよ」であった(簡単に大雑把に言えば)。私はちゃんとこの問題を解けた覚えがない。いや、はっきり言えばずいぶん悩んだ覚えしかない。ってことはいまいち解けなかったのだろう。なので、「落ちていくエレベーターの中の人達は無重力状態である」と聞くと、「ほんとう〜にそうか? ほんとう〜にそうか?」と歌いたくなる。
研究室関連では、絶対重力測定を行う研究をする人達もいたわけである。絶対重力(加速度)測定は自由落下する物体の運動を測定して、重力加速度を測定するわけであるが、そう簡単に物体は自由落下してくれないのである。簡単な実験で物体を自由落下させて重力加速度を測定してみるとわかるが、大雑把な実験(自分の家ですぐできる程度の)では一桁ちょいの精度しか出ない。一桁ちょいの精度しかでないということは、(例えば)体重が10%弱程度になったように感じるかもしれないが、それは無重力ではない。体重が60kgの人であれば、6kgも感じてしまうのである。(雑な話だが。)
空気中を落ちてくる雨だってそうだ。もし、雨が自由落下を続けていたらものすごいスピードになって、雨に打たれるのは命がけになってしまう。しかし、実際にはそんなことはない。空気抵抗で速度は飽和してしまい、自由落下状態ではないからである。
さて、本題である。果たして、
例えば、
- 若井研究室の研究概要
- http://mech.gifu-u.ac.jp/~wakailab/research/Basic/base_h.html
北海道の上砂川町にある施設(JAMIC)で、490m落下させることにより、10秒の無重量環境が得られます。落下中は空気抵抗を受けるので、落下カプセルを二重構造にし、空気抵抗を無視できるように工夫してあります。と、記述されているように、実際には工夫をこらさなければ無重力状態は実現できないのである。絶対重力系などでも空気抵抗を無視するために、投げ上げて往復運動を測定するなどの工夫がいるのである。
と、言葉だけで書いてもしょうがないので、適当な計算でもしてみる。いや、もちろん、実験をするのが良いわけであるが、面倒だし…
まずはエレベーターには、
- 何の抵抗も働かない
- 空気抵抗とワイヤーの抵抗が働く
そして、エレベーターの中の人には空気抵抗は働かないとした。エレベーターの中の空気と人の速度差はほとんどないからである。また、エレベーターは人よりもはるかに重く、人の重さはエレベーターの運動に何の影響も及ぼさないと近似した。
その計算の結果を以下に示す。これが落ちていくエレベーターの軌跡である。抵抗のない場合が(赤)で抵抗のある場合が(青)である。エレベーターが落ち始めてから30秒後までの軌跡である。
 |
理想的な場合(赤)に比べて、抵抗のある場合(青)の落ち具合が鈍っているのがわかると思う。それでは、もっと時間が経った場合はどうだろうか?それを次に示す。エレベーターが落ち始めて300秒後までの軌跡である。つまり、五分間もこのエレベーターは落ち続けているのである。落ちた距離は理想的な場合で40kmの深さに達している。すごいエレベーターである。こんなに落ち続けていると、すでに重力加速度が一定とは言っていられなくなる。
 |
ここまでくると、抵抗のない場合(赤)と抵抗のある場合(青)では全然違う軌跡になっている。抵抗のない場合(赤)では放物線そのものであるが、抵抗のある場合(青)では一定の速度になっている。
それでは、エレベーターがこのような状態になった時の、エレベーターの中の人に働く加速度(と実際の加速度の差分)を示してみる。これを見れば、落ちていくエレベーターの中の人が無重力状態であるかどうかがわかる。まずは、300秒後までの変化を見てみる。
 |
理想的な場合(赤)はずっとゼロすなわち無重力状態であるが、抵抗のある場合(青)は無重力状態は最初だけで、50秒後位には通常の状態に戻ってしまっている。最初の部分をもう少し拡大してみる。次に示すのは、3秒後までの落ちていくエレベーターの中の人に働く重力加速度(と実際の加速度の差分)である。
 |
これを見ると、あっという間に人は無重力状態ではなくなっているのがわかると思う。
というわけで、先の三つの選択肢、
- 床に張り付く
- 天井に張り付く
- 宙に浮かぶ
先日みたニュースのエレベーター落下実験の中で、中にいた男性リポーターが、落下しながら「ひぃ?」とアオ向けになった状態で床にハリ付いていたからなのです。という実際の現象が正しいのである(いや、もちろん状況はかなり異なるが)。「頭の中だけ」で考えたことというのは大抵の場合間違ってしまう。(もちろん、今回の「できるかな?」の話もその例外ではない)
そして、その後に、
ありはきっと、速度がそこまで充分でなかったのと、もしやのトキのために、男性リポーターに安全な姿勢をとらせていたタメだと思われます。とあるが、実際問題として「速度がそこまで充分」になることは未来永劫ないわけである。だから、(私の中では)エレベーターの中の男性リポーター氏は床から浮かぶことはないのである。
こういうのは、結局考える人の数だけ答えがあるのだと思う。もし、その内のどれが真実に一番近いかどうか知りたければ、実験すれば良いだけの話だし。
2000-02-27[n年前へ]
■「文学論」と光学系 
漱石の面白さ
前回、
でさて、モナリザと言うと、夏目漱石と「モナリサ」にも言及しなければならないだろう。と書いた。何しろ
- 恋の力学 三角関係編 - 恋の三体問題 - (1999.12.27)
- 草迷宮・空間'99 - ネコの目から見た世界- (1999.11.05)
- 「こころ」の中の「どうして?」-漱石の中の謎とその終焉 - (1999.09.10)
- 夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
- [Scraps]人静月同照 - ぼくらが旅に出る理由- (1999.06.17)
その漱石は「永日小品(リンク先は青空文庫)」(リンク先は青空文庫)の「モナリサ」中で
「モナリサの唇には女性(にょしょう)の謎(なぞ)がある。原始以降この謎を描き得たものはダ・ヴィンチだけである。この謎を解き得たものは一人もない。」と書いている。女性には興味がなかったとも言われ、ずっと付き添っていた男性との関係も噂されるダ・ヴィンチである。ここらへんは、果たしてどうか?とも思う。むしろ、新宿のホストクラブのホストの方が女性(にょしょう)の謎(なぞ)については詳しいのではないかとも私は考えたりもする。
が、そんなことはどうでも良い。漱石はレオナルド・ダ・ビンチのモナリザに興味を持ち、小品を書き上げたのである。そこで、漱石とダ・ヴィンチの相似点を考えてみたい。
レオナルド・ダ・ビンチの著作には「文学論」というものがある。漱石にも同じ名前の「文学論」がある。この「文学論」はこれまで読んだことがなかったのだが、
- 「漱石の美術愛」推理ノート 新関公子 平凡社 ISBN4-582-82927-9
- 遠近法
- 漱石の文学論の「公式」
これが、とても面白い。仮名遣いが古いため、なかなか目に入ってこないのであるが、とても面白い。これは絶対に文庫本にすべきである。眺めているだけでも面白い。
まずは、冒頭のフレーズがいきなりこうである。
およそ文学的内容の形式は(F+f)なることを要す。Fは焦点的印象又は観念を意味し、fはこれに付着する情緒を意味す。まるで、理系の教科書である。そして、目次(編)を大雑把にさらってみる。
- 文学的内容の分類
- 文学的内容の数量的変化
- 文学的内容の特質
- 文学的内容の相互関係
- 集合的F
また、「文学論」中では、例えば、浪漫派と写実派の違いについて数値的な比較を通じて述べられていたりする。実に「科学的」な思考による「文学論」である。いや本当に漱石は凄い。
さて、中の文章を解説する力は私にはない。そこで、中の図表を示してみることにする。そこで適当に思うことなどを書いてみようと思う。
次に示すのは、「文学論」の冒頭の方で「意識の焦点・波形」を説明した図である。
 漱石全集第十一巻より |
この図は人間が何かを感じるときには焦点にピークがある、そして、その周りはぼやけたものが連続的に続いているということを示したものだ。これなど、
の時の「恋のインパルス応答」を彷彿とさせる。あの時の「恋のインパルス応答」を次に示してみる。 |  |
この意識される恋心(f)は先の「意識の波形」と全く同じである。ある出来事(F)と、それに付着する情緒(f)を示したものとなるわけだ。付着する情緒(f)というのは中心が一番大きく、その周りにぼやけたものが繋がっているというわけである。人間の感じ方・情緒を光学系と結びつけているわけだ。
いやはや、「恋のインパルス応答」と同じようなことを考える人はやはりいるものである。まさかそれが漱石だとは思いもしなかった。しかも時代を考えると凄まじい、としか言いようがない。
そして、さらに次に示すのは
およそ文学的内容の形式は(F+f)なることを要す。Fは焦点的印象又は観念を意味し、fはこれに付着する情緒を意味す。ということを示す図である。先の - 「漱石の美術愛」推理ノート - ではこの図と遠近法の関連が述べられている。
 漱石全集第十一巻より |
ここで、縦軸は「時間」となっており、横軸は「色々な出来事」である。ある人が感じた「色々な出来事」を時間方向に収斂させていくと、そこには「作者自身の視点がある」というわけだ。これが漱石の言う「文学論」の中心である。
この図などカメラや望遠鏡の光学系を彷彿とさせる。「光学系の一例」を以下に示す。
 |
先の「文学の焦点」を示した図はレンズで光を焦点に集めるのと全く同じだ。いや、「焦点から光を投光する」のと同じと言った方が良いだろうか。以前、
で、景色に焦点を合わせて、フィルムに結像させるのがカメラだ。しかし、フィルムに写っているのは単なる景色ではない。カメラの光が集まる焦点にフィルムが位置していると思い込むとわからなくなる。逆から考えてみれば簡単に判るはずだ。カメラの視点にフィルムが位置しているのだ。フィルムに景色が写っているのではなく、フィルムが景色を選び、景色を切り取っているのである。と書いたのと全く同じである。その光学系には歪みもあるかもしれないし、色フィルターもかかっているかもしれない。しかし、とにかく焦点にはその人自身がいるのである。写真に写っているのは、撮影者の視点なのである。写真を見れば、撮影者が、どこに立ち、何を見てるかが浮かび上がってくるはずである。フィルムに写っているのは撮影者自身なのだ。
写真でも文章でもとにかく何であっても、色々感じたことを表現していく時、その焦点には表現者自身がいる。私の大好きなこの2000/2/25の日記なんか、実にそれを感じるのである。
2000-05-10[n年前へ]
■「モナ・リザ」の背景と自己相似性 
フラクタル地形を作ろう
以前、
で、「モナリザ」の微笑はどうにも奥深く見えるから不思議である。その微笑の先に何があるのかを深く考えさせる。そして、その答えはなかなか見つけられない。「モナリザの微笑」を眺め考えると、その先には結局「モナリザ」しか見えてこない。答えが見えないのであると書いた。そして、画像を読み込み、その画像をその画像自身の縮小画像(48x48個)で表現するjoconde.exeを作成し、自己相似形の「モナ・リザ」を描いてみた。それが、この下のjunhirabayashi 作 48x48の「モナリザ」である。
 |
ところで、本家のダ・ビンチの「モナ・リザ」と言えば、本当に奇妙な背景である。荒涼として、とても普通の景色とは思えない。地学の教科書に出てきそうな地形だ。グランド・キャニオンのような侵食地形のようである。
 |
ダ・ビンチは治水に関して深く興味を持ち、大好きだったと聞く(いや、もちろん本当に聞いたわけじゃないけれど)。ダ・ビンチは治水に関してはプロフェッショナルだった。それを考えれば、この「モナ・リザ」の荒涼たる背景なども、ダ・ビンチの趣味そのままのようで面白く感じられる。しかし、見れば見るほどこの背景は不思議である。Bryce等の「自然っぽい地形」を描いてくれるソフトで作成した景色のようである。
その手のソフトは想像上の地形を作成するのに大抵フラクタルを用いる。つまり、フラクタル地形である。フラクタル地形というのは、例えば山脈の一部分を拡大してみてもそこにはやはりその山脈自身と同じような高低があるということである。どんなに拡大してみてもそこにはやはり小さな山脈があるのだ。というよりは、どんなに拡大してみても、小さな山あり谷ありと言った方が良いだろうか。そういう自己相似性を利用してやれば「自然っぽい地形」を描けるわけだ。
「モナ・リザ」の微笑の中はどこまで拡大しても「モナ・リザ」の微笑がある、つまり「モナ・リザ」の前景は感覚としてのフラクタル性を持っているように感じられる。そして、背景もまたフラクタル性を顕著に持つフラクタル地形っぽいのである。ダ・ビンチが自己相似性、フラクタルについて考えていたと想像してみると、とても面白いと思う。
さて、フラクタル地形の説明を少しだけ書いたが、やはりここは自分でもそのフラクタル地形を作成してみなければマズイだろう。何しろ、私はフラクタル地形のことは良く知らない。とりあえず、自分で作成してみないことにはよくわからない。まずは実践あるのみだ(もちろん、トンデモナイ内容を実践するのは問題外だ)。
そこで、まずは手っ取り早くMathematicaでフラクタル地形を作成してみた。次のアニメーションGIF画像はMathematicaでフラクタル地形を作成していく様子である。荒いスケールの凹凸を作成して、その後段段と細かいスケールの凹凸を作成していくようにしてみた。プログラム時間は10分である。ここらへんの手軽さがMathematicaのスゴイ所だ。
 |
この計算は適当に作ってみただけなので色々と問題がある。例えば原点(0,0)から放射状に凹凸がある。これは計算上の問題である。しかし、今回は面倒なので深追いはしない(カッコつけて言う内容じゃないが…)。これを手直ししようとするととたんに面倒になってしまうのである。
とりあえず、完成したフラクタル地形は次のようになる。hirax山脈とでも名づけておこう。
 |
なかなか「自然な山脈」っぽくないだろうか?青い光に照らされた幻想的な山脈である。といっても、色がなんとも自然でなくて、「自然な山脈」には見えないという人も多いだろう。というわけで、色調を変えて、それっぽくしてみた。そこで、次が先の完成画像の色調を変えて、「自然っぽく」したフラクタル地形である。
 |
これが、Mathematicaで作成した「山岳地形」だ。結構、それっぽく見えると思う。今回は、Mathematicaの内部でレンダリングしたそのままであるが、次回(といっても、いつになるかわからないのはいつものこと)には、Mathematicaで作成した「山岳地形」を元にきちんとレンダリングしてみたいと思う。さぞや、幻想的な景色が作成できるに違いない。
さて、私はフラクタル図形を眺めているとなぜだか知らないが、水戸黄門の主題歌が頭の中で響いてくるのである。あの、「人生楽ありゃ苦もあるさ…」というヤツである。もう、流れ出したら止まらないのだ。それはもう水戸黄門の主題歌のフラクタルである。
そして、ひどい時には「どんぐりころころ」と水戸黄門の主題歌の輪唱が頭の中で始まってしまったりするのだ。それを「カノン」と言えば聞こえは良いが、いやもうホントにたまらない状態である。
どんぐりころころ、どんぐりこ人生楽ありゃ、苦もあるさお池にはまって、さぁ大変くじけりゃ、誰かが先に行く…
あぁ、止めてくれぇ…
2000-10-25[n年前へ]
■虹の彼方に。 
色覚モドキソフトを作る その7
今年は好きなWEBサイトがいくつも店じまいしてしまった。「わきめも」もそんなサイトの一つだ。その今はもうない「わきめも」の中で、きれいな虹が見えた。だからビールを飲んだ。だけど、目に見えている虹の色は写真のフィルムには写らない。どんなフィルム・CRT・プリンターの出力色空間もとても狭くて、虹の中に見える色は出せないからだ。ビールも虹も「生」に限る。という話があった。もう元のWEBページがあるわけじゃないから、細かいところは違っていたかもしれないけれど、大雑把な内容はこんな感じだった。- ビールも虹も「生」に限る - なんてとてもシブイセリフで良い感じだ。
このセリフの中の「どんなフィルム・CRT・プリンターの出力色空間もとても狭くて、虹の中に見える色は出せないからだ。」というのを図示してみると、下の図のようになる。
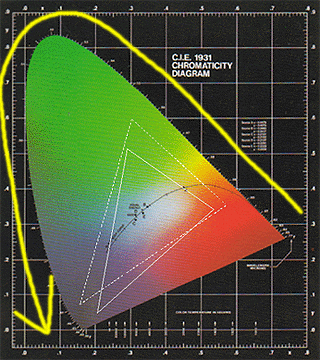 |
例えば、虹の中に見えるスペクトル色はこの図で言うと、黄色の矢印で描いた側の、色で塗りつぶした領域の外枠の色だ。波長の長い単色光、つまり最初は赤色から始まって、波長が短くなるに従い「赤→黄色→緑→青→紫」というようにスペクトル色はつながっている。
この図中に、とあるCRTとプリンターの出力可能な色空間(CCMファイル中に埋め込まれているプロファイル情報を参考にしたもの)を白点線と白実線で示したが、とても狭い領域の色しか出せず、とてもじゃないが虹の中に見えるスペクトル色はこれらの機器では出ないことが判るだろう。
だから、「生」の虹を見たときの感じは写真でもCRTでもプリンターの出力でも味わえないわけだ。おいしいビールは「生」に限る(私の趣味では)のと同じく、虹も「生」に限るのだ。
だから、虹の色と同じ
の時に撮影したような太陽光のスペクトルも、こんな風にWEBページの上で眺めても、それはやっぱり分光器を「生」で覗いている感じはとてもじゃないが味わえない。 |
こんな、「赤→黄色→緑→青→紫」というスペクトル色を眺めていると、中学の頃の美術の授業を思い出した。その授業の中で、こんな色相環が教科書か何かに載っていて、「こんな色のつながりは「赤→黄色→緑→青→紫」というスペクトル色に対応しているんだよ」と美術の先生に言われた。それを聞いていた私はよく判らなくなって、「すると、何で紫と赤のところで繋がってるのでしょうか??」と先生に聞くと、その先生も「う〜ん。」と悩み始め、しまいには「いつか調べて答えが判ったら、私にも教えてくれたまえ。」と言うのである。今考えてみると、それはとても素晴らしい言葉だった(間違っても皮肉でなくて、本当に素晴らしいと思うのだ)。
 色覚のメカニズム 内川恵二 朝倉書店 口絵より |
だけど、「赤→黄色→緑→青→紫」という単色光のスペクトルが波長としては単に一方向に変化していくだけなのに、グルっと一周する感覚を受けるのはとても不思議である。そこで、色感覚モドキソフトを作ってそこらへんの感覚を眺めてみる、つまり「できるかな?」の常套手段である「その謎を見てみよう」と思うのである。
この「色感覚モドキソフト」はいつものように極めて大雑把でチャチな作りである。ソフトの流れとしては次に示すように、
1.光源としては二種類の場合
- RGBのCRTモニタ
- 単色スペクトル光
2.画像を読み込み、画像の任意の場所のRGB値を元に光全体としてのスペクトルを計算する。
3.錐体の分光感度を適当に設定し、Boynton色覚モデルをもとに
- 「赤<->緑」チャンネル
「青<->黄」チャンネル
「輝度」チャンネル
ここに今回作成したtruecolor7を置いておく。細かい使い方は今回は割愛したい。が、多分少し使えば(使う人がいるともそうそう思えないが)、使い方はすぐに判ると思う。
- truecolor7.lzh 522KB
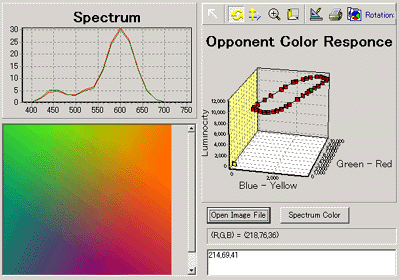
truecolor7の動作画面はこんな感じである。
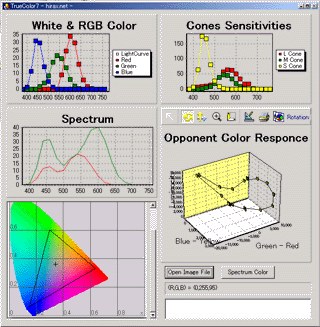 |
左上から下に向かって、RGBそれぞれのスペクトル設定、全体でのスペクトル、読み込んだ画像、右上から、錐体の分光感度、反対色応答の出力値である。
画像の任意の場所を調べたければ、BMP画像を読み込んでマウスで好きな場所をなぞるなり、クリックすればよいし、「赤→黄色→緑→青→紫」という単色光のスペクトル色の場合を計算したければ、右下にある「SpectrumColor」ボタンを押せば良い。
さっそく、赤→黄色→緑→青→紫というスペクトル色の反対色応答「モドキ」を見てみたのが次のグラフである。縦軸が「輝度チャンネル」で、向かって左の軸が「青<->黄」チャンネルで、向かって右の軸が「赤<->緑」チャンネルである。この「輝度チャンネル」・「青<->黄」・「赤<->緑」という「感覚的」3次元空間で波長が一方向に変化するスペクトル色を連続的にプロットしてみると、見事に円状につながっていることが判る。「赤<->緑」チャンネルの計算が基本的にはL錐体出力からM錐体出力の差分をとって、さらにS錐体の出力をほんの少しだけ引いてやるという計算をしているため、短波長側でL錐体の感度がM錐体の感度を上回っている(ように実は設定した)のでこんな風になるのだ。単純に波長が短くなるだけなのに、見た感じ何故か紫と赤が近く見える。あくまで、大雑把な話だけれど。
中学の頃の私がこれで納得するとは思えないが、少なくとも今の私はこの円環構造を目にすることができればこれで満足である。
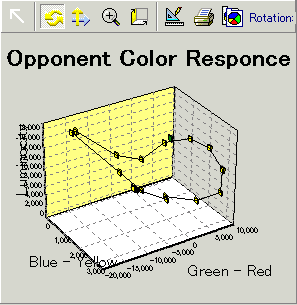 |
ちなみに、つぎに示すのは輝度が一定になるようにした画像の周辺部をグルッと計算してみたものである。このグラフでは縦軸の「輝度チャンネル」の値はずっと同じで、「青<->黄」チャンネル・「赤<->緑」チャンネル平面内で円環状にグルッと一周しているのがわかると思う。自分自身が下の画像を眺めたときに、つながりが自然だなぁ、あるいは自然じゃないなぁ、と感じる感覚と重ね合わせながら見てみると面白いのではないだろうか。
 |
さて、興味がある方がいらっしゃれば、このバッタもんソフトを使って、ぜひ色々なパラメータを振って色々な画像を読み込んで試行錯誤をしてみてもらいたいと思う。そして、その結果を私に教えていただければとてもうれしい。もちろん、このソフトを使うという話に限らず、面白そうなアイデアがあれば大歓迎である。
さて、虹というとミュージカル「オズの魔法使い」の中でジュディ・ガーランドが歌っていた"OverThe Rainbow"を何故か思い出す。実は、このソフトを作っているときも「ふ〜ん、ふ〜ん、ふ〜んふんふふふ〜ん」と歌詞が判らないまま鼻歌を歌いながら作業していた。歌詞が判らないまま、というのも何なので、せっかくなので調べた歌詞で今回の話を終わらせたいと思う。虹の彼方には…
Somewhere, over the rainbow, skies are blue.And the dreams that you dare to dream really do come true.
2000-12-02[n年前へ]
■ブランコの中の∞(無限大) その4 
mail 実は私は,まじめにブランコの制御を研究していまして,実際にブランコロボットを製作し実験しました.その様子は(リンク)にありますので,ご覧ください. ブランコがなぜこげるかは,数式を使うと簡単に説明できるのですが,直観的に説明しようとするとなかなか難しいものです.物理の教科書にも,これまでなかなかいい説明が載っていなかったので,僕も学生には角運動量の話を使って説明していました.今回,同じ論法で説明されている方を見つけて大変感激しております.次回のパラメータ励振の話も楽しみにしています. < Thank you. jun hirabayashi 「次回のパラメータ励振の話」を読んで失望されていないことを、ただただ願うのみです。ハイ。