hirax.net::Keywords::「図書館」のブログ

■「文学論」と光学系　

漱石の面白さ

　前回、

• 「モナリザ」の自己相似形 - 48x48の「世界への微笑」- (2000.02.24)

さて、モナリザと言うと、夏目漱石と「モナリサ」にも言及しなければならないだろう。

• 恋の力学　三角関係編 - 恋の三体問題 - (1999.12.27)
• 草迷宮・空間'99 - ネコの目から見た世界- (1999.11.05)
• 「こころ」の中の「どうして?」-漱石の中の謎とその終焉 - (1999.09.10)
• 夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
• [Scraps]人静月同照 - ぼくらが旅に出る理由- (1999.06.17)

　その漱石は「永日小品(リンク先は青空文庫)」(リンク先は青空文庫)の「モナリサ」中で

「モナリサの唇には女性（にょしょう）の謎（なぞ）がある。原始以降この謎を描き得たものはダ・ヴィンチだけである。この謎を解き得たものは一人もない。」

　レオナルド・ダ・ビンチの著作には「文学論」というものがある。漱石にも同じ名前の「文学論」がある。この「文学論」はこれまで読んだことがなかったのだが、

• 「漱石の美術愛」推理ノート　新関公子　平凡社　ISBN4-582-82927-9

• 遠近法
• 漱石の文学論の「公式」

　これが、とても面白い。仮名遣いが古いため、なかなか目に入ってこないのであるが、とても面白い。これは絶対に文庫本にすべきである。眺めているだけでも面白い。

　まずは、冒頭のフレーズがいきなりこうである。

　およそ文学的内容の形式は(F+f)なることを要す。Fは焦点的印象又は観念を意味し、fはこれに付着する情緒を意味す。

1. 文学的内容の分類
2. 文学的内容の数量的変化
3. 文学的内容の特質
4. 文学的内容の相互関係
5. 集合的F

　さて、中の文章を解説する力は私にはない。そこで、中の図表を示してみることにする。そこで適当に思うことなどを書いてみようと思う。

　次に示すのは、「文学論」の冒頭の方で「意識の焦点・波形」を説明した図である。
 

意識の焦点・波形

漱石全集第十一巻より

　この図は人間が何かを感じるときには焦点にピークがある、そして、その周りはぼやけたものが連続的に続いているということを示したものだ。これなど、

• ぼやけた測定系でシャープな測定をしたい-恋のインパルス応答 WhiteDay記念 - (1999.03.14)

左：出会い(F)、右：それにより意識される恋心(f)

　この意識される恋心(f)は先の「意識の波形」と全く同じである。ある出来事(F)と、それに付着する情緒(f)を示したものとなるわけだ。付着する情緒(f)というのは中心が一番大きく、その周りにぼやけたものが繋がっているというわけである。人間の感じ方・情緒を光学系と結びつけているわけだ。
　いやはや、「恋のインパルス応答」と同じようなことを考える人はやはりいるものである。まさかそれが漱石だとは思いもしなかった。しかも時代を考えると凄まじい、としか言いようがない。

　そして、さらに次に示すのは

　およそ文学的内容の形式は(F+f)なることを要す。Fは焦点的印象又は観念を意味し、fはこれに付着する情緒を意味す。

「文学の焦点」

漱石全集第十一巻より

　ここで、縦軸は「時間」となっており、横軸は「色々な出来事」である。ある人が感じた「色々な出来事」を時間方向に収斂させていくと、そこには「作者自身の視点がある」というわけだ。これが漱石の言う「文学論」の中心である。

　この図などカメラや望遠鏡の光学系を彷彿とさせる。「光学系の一例」を以下に示す。
 

「光学系の一例」

　先の「文学の焦点」を示した図はレンズで光を焦点に集めるのと全く同じだ。いや、「焦点から光を投光する」のと同じと言った方が良いだろうか。以前、

• [Scraps]視点 - ここにいるよ - (1999.07.24)

　景色に焦点を合わせて、フィルムに結像させるのがカメラだ。しかし、フィルムに写っているのは単なる景色ではない。カメラの光が集まる焦点にフィルムが位置していると思い込むとわからなくなる。逆から考えてみれば簡単に判るはずだ。カメラの視点にフィルムが位置しているのだ。フィルムに景色が写っているのではなく、フィルムが景色を選び、景色を切り取っているのである。

　写真に写っているのは、撮影者の視点なのである。写真を見れば、撮影者が、どこに立ち、何を見てるかが浮かび上がってくるはずである。フィルムに写っているのは撮影者自身なのだ。

　写真でも文章でもとにかく何であっても、色々感じたことを表現していく時、その焦点には表現者自身がいる。私の大好きなこの2000/2/25の日記なんか、実にそれを感じるのである。
 

■書籍デジタル化委員会(電子図書館)　

（リンク）from http://www2s.biglobe.ne.jp/~ryo2/diary000131.html

■あの小判で何が買えたの？　

「夏休みの自由研究」図書館で江戸時代の物価を調べてみた

　夏休みも終り、また忙しい生活が始まった。忙しい生活をしていると、「あぁ昔のノンビリとした時代、例えば江戸時代に戻りた〜い」なんて思ってしまう。江戸時代のお気楽な町人かなんかに生まれ変わって、ぼぉ〜っとしてみたり、祭りや火事に興奮してみたり、たまには働いてみたり、そして時には近所の町娘と恋なんかして過ごしてみたりしたいなぁ、と思ってみたりするのである。それに、江戸時代と言えば大昔なのだから、きっと物価はものすごく安いに違いないのである。平均給料がいくらだか知らないが、きっと色々なモノが安く買えるに違いないのだ。

　といっても、私は歴史にはとっても疎い（いや違った、「歴史も」だ）ので、本当のところ江戸時代がそんなノンビリとした時代だったかどうかは知らない。まぁ、知らないからこそ、適当にこんな風に楽観的に思ってしまったりするのである。

　しかし、世の中には私のような「歴史知らず人間」だけでなくて、「歩く歴史」人間のような方々も多いのである。いや、こう書くといきなり誤解されてしまいそうだ。私は別に「歩く化石」人間が多いとか、「踊るシーラカンス」人間が多いとか言いたいわけではないのである。旧人類が満ち溢れていると言いたいわけではないのである。私は、単に世の中には「歴史大好き」人間が多い、ということを言いたいだけなのだ。そう、例えば歴史大好き人間、例えば時代劇大好き人間(*1)とか幕末野郎(*2)とか戦国野郎(*3)などはきっと誰の周りにもいるハズなのである。
 

(*1)　古くは「杉さまぁぁ〜」と黄色い声を上げる杉良太郎大好き・時代劇大好きおばちゃん（いや、違ったおねえさん…）、など。
(*2)　坂本竜馬に自分を例える武田鉄也、など。
(*3)　会社から外へ飛び出し、その退社時に「江戸城」という本を後輩に渡して行くようなカッコイイ人、など。

　そこで、今回夏休みのぼ〜っとした気分からのリハビリも兼ねて、江戸時代と現代の物価について調べてみることにした。そして、夏休み過ぎの私が夢想する「江戸時代への憧れ」がトンチンカンなものなのか、あるいはそうでないのかを調べてみたい、と思う。つまり、今回は単に「夏休みの自由研究　図書館で江戸時代の物価を調べてみた」ということなのである。そして、「江戸時代はきっと色々なモノが安く買えるんだ〜。いいなぁ〜。」の是非を確かめることにしよう。

　とはいっても、じゃぁ、すぐに江戸時代の物価と現代の物価を比べよう、といきなり始めるわけにはいかないだろう。なんと言っても、江戸時代は実に長い。何しろ、江戸時代と一言で言っても、260年もあるのだ。その長い江戸時代の間にお金の価値（物価）がものすごく変化していたとしたら、一体どれが「平均的」江戸時代なのか判らない。

　そこで、まずは図書館に行って、「江戸物価辞典」を片手に江戸時代の間に米の価格がどの程度変化していたのかをグラフにしてみた。江戸時代の間に物価がどの程度変化していたかを見てみるわけだ。もちろん、何をもって物価の上昇具合が緩やかなのかあるいは急なのか、という基準が必要なわけで、第二次大戦後の米価格の変化も同じように示してみた。
 
 

米の価格の変化
左　：　江戸時代
右　：　第二次大戦後

　上のグラフを眺めてみると、江戸時代（幕末期は除く）は緩やかな物価上昇は見られるが、それはごくごく緩やかなものであることが判る。何しろ200年も経っても、たかだか二倍程度にしか上昇していないのである。第二次大戦後の（すなわち、たった50年程度の間の）物価上昇に比べれば、もう物価上昇はほとんど無いといっても良いくらいである。少なくとも人生50年というような時間尺度で眺める限りは物価はほとんど変化していないのである。私の記憶（とても曖昧…）があるたった25年足らずの間に、駄菓子の価格がほとんど二倍（ガリガリ君を除く）になっているのとは大違いなのだ。ということは、少なくとも江戸時代の中期辺りの物価を眺めてみれば、それを「江戸時代」と言ってしまっても良さそうに思える。そこで、

• http://hiden.cup.com/jdi3html/shop_ls.html

• 今の方が安いモノ
• 昔の方が安かったモノ

　とはいえ、もちろん江戸時代にあったが現在はもうほとんど存在しないというようなものも多い。そこで、そういうものは現在における相当品で、例えば

• 富くじ　→　宝くじ
• 吉原高級遊女　→　銀座の高級？クラブの基本料金
• 町駕籠　→　タクシーの初乗り料金
• 夜なきソバ　→　近所のチャルメラ・ラーメン
• 絵本　→　写真集
• 貸し本　→　レンタルビデオ
• 夜鷹　→　○×△■

　また、モノの価格だけでなく「収入」の基準もやはり必要なわけで、それに対しては大工日当を用いた。つまり、収入の基準との大工日当に対して、色々なモノがいくらであるかを、江戸時代と現在とで比べてみることになる。というわけで、そのグラフが以下である。
 

大工日当を中心に見た、
青線　：　江戸時代中期のモノの価格
赤線　：　西暦2001年のモノの価格(hirax.net主観による)
緑線　：　両者の比較

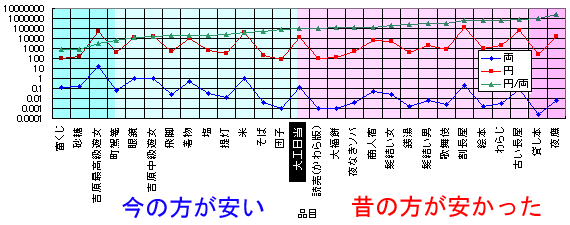　このグラフを見ると、例えば大工日当を基準にすると、一両はほぼ十万円に相当することが判る。また、砂糖などは今のほうが江戸時代よりもよっぽど安い。だから、砂糖を基準にすれば、一両は千円にしかならない。逆に夜鷹を基準にしてしまうと、何と一両はおよそ百万円に相当するのである。それほどに江戸時代の夜鷹は安かったのだろう。大変な話だ…。

　砂糖も含め、眼鏡とか町駕籠（タクシー）とか飛脚（宅急便）とか提灯（懐中電灯）とかの、いわゆる科学の力を有効活用したものは当然現代の方が安い。そして、わらじとか歌舞伎とかの現代においては希少価値の高いものは江戸時代の方が安かったのも当然である。じゃぁ、吉原高級遊女（銀座の高級？クラブの基本料金）と吉原中級遊女（銀座の大衆クラブ）の価格の違いはどう説明するのかいう疑問も当然湧いてくるわけではあるが、そういう話はどうでも良いのだ。

　何はともあれ、タクシー（町駕籠）に乗って銀座のクラブ（吉原高級遊女）に遊びに行くのが大好きな人、しかも眼鏡をかけてて、甘いもの（砂糖）が大好きなんて人には江戸時代はどうも合いそうにない。そんな人たちはすごくお金持ちでないと、江戸時代はかなりツライ時代のようである。そんな人達は、江戸時代よりも2001年現在の方が幸せに違いない。そんな輩には江戸時代はマッチしないハズなのである（根拠薄弱）。

　しかし、広い風呂（銭湯）が好きで、夜のチャルメラ・ラーメン（夜鳴きソバ）にロマンを感じ、写真集（絵本）が欲しいけど高くて買えないワタシのような人間にはやはり江戸時代がジャストフィットするに違いないのだ。チープにお気楽に生活できるかもしれないのである。やはり、「江戸時代はきっと色々なモノが安く買えるんだ〜。いいなぁ〜。」は合っていたのである（ウソ）。

　よっしゃぁ、私に合う時代はやっぱり江戸時代なのだぁ、とここまでは思ったのだが、もう少し私の生活パターンを考慮して吟味し調べてみると（調べなくても判るだろうが…）、江戸時代には発泡酒はもちろんビールは日本では一般的ではなかったのである。これでは、ビール（だけどお金が無いから発泡酒に変わったが）大好き人間の私としては致命的にマズイのであった…。う〜ん、う〜ん、ちょっと残念なんだけどだなぁ…。
 
 

■私と二度めに出会う「水」　

クリスマスの小さな遺品

　先日、こんなメールを頂いた。

　私の娘は小学三年生。図書館から借りてきた「水の一生」といった、子供向け科学本（蛇口から出た水は下水を通って…<途中大幅に省略>…再度雨になって…というヤツです）を読んでおりました。そこで彼女はいくつかの疑問を口にしました。

「一度下水に流した水は、どのくらい経ったらまた私のところへ戻ってくるの？」
 

私　「必ずしもすべての水が海まで行くわけではなくて、下水処理場で蒸発して、川の取水口あたりで雨になる分子もあるはずだから、そうだなあ、一番早くて３日くらいかなあ。　勿論もっと長い場合もあるし、一度流したらキミが生きている間にはここには戻ってこない分子もあると思うよ」

「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」

私　「う〜ん…　　どれくらいなんだろう？」

　さて、どう思われますか？

　ところで、この後半の疑問「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」というのはたまに見かける話である。何かの小説で、「このコップの話が主人公が科学を志したきっかけになっている」という小道具に使われている例も読んだことがあるような気がする。

　たまに見かける話ではあるのだけれど、同じ本を読んでも人それぞれ抱く感想は違うし、私なりにも考えてみたい気もしたので、今回はこの「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」を考えてみることにした。

　人が一日に「出会う」水はどの位の量だろうか？成人男子が安静にした状態で、一日当たり大体2.5リットルの水を消費するという。すると、小さい子供の場合でも、少なくとも一日2リットルくらいは水を消費する、つまり水と「出会って」そして「分かれる」ことになる。2リットルの水というと、2000gだから、これを水の1molあたりの重さ18g /molで割って、さらにアボガドロ数（1mol当たりの分子数）をかけてやると、(2l = 2000g ) / 18g x 6.022x10²³個 = 6.7 x 10²⁵個となり、私たちが一日に出会う水分子の数の個数がわかる。

　この「とある一日に私たちが出会った水」が川へ流れて、海へ流れて、地球上にまんべんなく拡がったとしよう。地球上の限りなくある水の中に含まれる「とある一日に私たちが出会った水分子」の割合は、いったいどのくらいの程度になるのだろうか？

　地球上の水は大体14億km³くらいだという。そのほとんどは96.5%は海水で、残りが陸地のさまざまな場所（そしてわずかに空気中）に存在している。この地球上にある水の重さを計算すると、14億km³= 1350000000km³ = 1.4 x 10⁹ x 10¹² kg= 1.4 x 10²⁴ g ということになって、これを水の1molあたりの重さ18g /molで割ってやると、地球上に存在する水分子の総量は 1.4 x 10²⁴/ 18 = 7.8 x 10²²mol ということになる。mol数から水分子の量に直すために、アボガドロ数6.022x10²³個/molをかけてやると、地球上の水分子の総量= 4.5 x 10⁴⁶ 個という数字が得られる。

　すると、地球上の限りなくある水の中に含まれる「とある一日に私たちが出会った水分子」の割合は
「とある一日に私たちが出会った水分子」 / 地球上の水分子の総量 = 6.7x 10²⁵個 / 4.5 x 10⁴⁶ 個 = 1.5 x 10^-21= 0.00000000000000000015%というとても小さい割合になる。この割合は、新たに水分子と出会った時に、その水分子が「とある一日に私たちが出会った水」である確率と言い換えても良いだろう。とにかく、私たちの普段の生活の感覚からすれば、限りなく小さく思えてしまう。しかし、その再会の確率はとても小さく思えてしまうのだけれど、決して私たちは「とある一日に私たちが出会った水分子二度と水と再会しない」わけでは無いのである。

　例えば、180mlのコップ一杯の水の中には( 180ml = 180g ) / 18g x 6.022x10²³個= 6.0 x 10²⁴個の水分子が含まれている。ということは、このコップ一杯に含まれる水分子の中にいる、かつて「とある一日に私たちが出会った水分子」の数を計算してみると、
コップ一杯に含まれる水分子の数 x 「とある一日に私たちが出会った水」である確率= 6.0 x 10²⁴個 x 1.5 x 10^-21  = 9000個ということになる。コップ一杯の水の中にはかつて「とある一日に私たちが出会った水」が一万個近くも存在していることになる。

　しかも、この計算は「とある一日に私たちが出会った水分子」だけで計算していて、決して「これまでに私たちが出会った水分子」で計算しているわけではないのだから、「コップ一杯の水の中で、私と２度目に出会う水」はもっと多いことになる。もちろん、実際には私たちが消費した水が理想的に拡散したりはしないだろうから、こんな風に上手くはいかないだろうけれども。

　とりあえず、「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」という疑問を口にした小学校三年生の娘さんには、「ずっと昔のある日に出会った水がコップ一杯の中には一万個近くもあるかもね」と答えておくのが良いかもしれない。計算の中身、アボガドロ数なんて言っても、小学校三年生では「あぼがど？あぼがろど…？」と頭がこんがらがるだけかもしれないけれど、とりあえず「おとーさんって、何でもわかるんだー」とちょっとくらいは尊敬されたりするかもしれない。
 

　そういえば、先日東京で初雪が降った。「雪は天から送られた手紙」とは中谷宇吉郎の残した名言だけど、その雪を見ながらこんなことを考えた。

　ある日誰かが亡くなり、荼毘に付される。すると、その人の体のほとんどの部分は火と共に空へ昇っていくことだろう。成人の体のおよそ60%は水分だから、体重60kgの人であれば、その60%の36000gもの水が空へ還ってゆくことになる。その空へ還っていった水分子が世界中に散らばっていった後に、いつかまたその水分子と出会うためにはどの程度の水があれば良いだろうか？どの程度の水があれば、この中には「かつてあの人と共に空に帰っていった水分子」が一個くらいはある、と言えるものだろうか？

　これを先程と同じように計算してみると、ほんのちょっと「1 x 10^-3g」ほどの水があれば、その中には「かつてあの人と共に空に帰っていった水分子」が一個くらいある、という結果になる。「1x 10^-3g」ということは、大きさで言うと1mm³ほどになる。ちょうど雨粒一滴と同じ位の大きさだ。空から降ってくる雨一粒の中には「かつて亡くなった人と共に空に帰っていった水分子」が１個が漂っている、ということになる。

　冬の雪の一片の大きさが雨の一粒と同じくらいであるかは判らないけれど、今日のように何時の間にか雨が雪に変わることもあるくらいだから、やっぱり雪も雨と同じような大きさなのだろう。だとすれば、空から降ってくる雪の一片の中には、「かつて亡くなった人と共に空に帰っていった水分子」が１個宝石のように入っていてもおかしくはない。「雪は天から送られた手紙」であるならば、その中にはその手紙を天から送ってくる「かつて亡くなった人」のまるで遺品が１個づつ封じ込められているのである。「雪は天からの遺品」と言っても良いかもしれない。

　間もなく、クリスマス。そして、クリスマスには白い雪が付き物だ。空から舞い降りてくる白い雪の中には大切な１個の水分子「クリスマスの小さな遺品」が入っているのである。

■徳川埋蔵金殺人事件　

超論理特許ミステリー「狩野埋蔵金の埋蔵場所を解読し発掘する方法」

　ワタシの勤務先では「一年に＊本特許を書くべし」という恐ろしいノルマがある。もちろん、こまめに書いていれば何の問題もないのだけれど、他の仕事にかまけてついつい後回しにしていたりすると、年末や期末には特許をまとめて書かなければならなくなる。架空の物語を量産する小説家のように、架空の実験データを描き整理し、架空の特許を量産しなければならなくなるのである。

　いつものごとく、昨年末もそうだった。年末の最後の二三日は特許書きで追いつめられ、しかも書き上げられずに、できの悪い小学生のように、家へ書きかけの特許を持ち帰って、正月休みに特許を書かなければならなくなったりしていたのである。そんなわけで、正月番組を見ながら、特許庁の電子図書館のサイトにアクセスし特許調査をしつつ特許を書いていた。が、正月番組などを眺めているせいか、どうにもマジメに特許が書けなかったりするのである。いつしか、ビールを飲みながら仕事とは全然関係無い特許公報を眺めていたりしたのである。

　今回、紹介する特開2001-42765「狩野埋蔵金の埋蔵場所を解読し発掘する方法」という公開特許公報もその一つである。キャッチーな名前で想像つくとは思うが、なんとこの特許出願はいわゆる赤城山徳川埋蔵金の場所を発掘するための特許なのである。世に出される特許は数多く、埋め立てゴミの数より多いくらいかもしれないが、そんな中でも「埋蔵金の隠し場所を解読し発掘する方法」なんて特許は見たことがない。歴史ミステリー、暗号ミステリー、そして、ご当地モノミステリーなどが好きなワタシは思わず目を奪われ、その特許を読み始め、そしてこの超論理特許ミステリーの世界に引き込まれたのだった。

　そして、この特許のあまりの素晴らしさに今回こんな感想文を書いて、世の中にこの超論理特許ミステリー特許を広めたいと思うのである。そして、さらにはこの感想文を読んだ人が特許フォーマットに慣れ親しみスラスラと特許を書けるようになり、ワタシのように特許を書き残しで苦しむ人が減ることを強く望む次第なのである。
 

　さて、特許では、まず「発明の名称」を書かなければならない。この特許でももちろんそうだ。というわけで、
「発明の名称」　狩野埋蔵金の埋蔵場所を解読し発掘する方法
　
　何とも、キャッチーな名前である。これが火曜サスペンス劇場であれば、「徳川赤城山埋蔵金全裸殺人事件２ 湯けむり露天風呂で美人女子大生が消えた！村に残る伝説が不気味に今よみがえる！」くらいにはパワーアップすることだろうが、特許の書類としては十分に魅力的である。この名前を見れば、誰しもワタシのようにこの特許の世界に引き込まれるハズである。

　そして、次に「どんな範囲のこと」を特許として宣言するかを書くわけだ。これを請求項と呼ぶが、この特許はもちろんこれだ。
「請求項」　従来一般に赤城山徳川埋蔵金といわれている黄金の埋蔵場所を発見・発掘すること

　なんと、赤城山徳川埋蔵金といわれている黄金の埋蔵場所を発見・発掘してしまうのである。特許を書いて大金を手に入れるという話はたまに聞くが、特許を書いて埋蔵金を手に入れるという話は聞いたことがない。まさに、夢というか、男のロマンというか素晴らしい特許なのである。

　そして、次に「従来の技術」というセクションが続く。つまり、従来はこんな問題がありますよ、こんなに不便だったのですよ、ということを書くのである。それに対して、今回書いたこの技術はそんな「従来の課題」を解決できて、価値があるのですよ、と訴えるのだ。そこで、この特許は説く、

「従来の技術」　従来の技術は、解読に科学性が不足していたために、経済効果の悪いものであった。…暗号のかたちで示されている埋蔵金を資源として再利用するためには、闇雲に探したのでは経済的に成り立たないので技術とは言えない。埋蔵金の探査技術が発達すれば、埋蔵金の発掘は夢や学問でなく産業になるであろう

　なんと、これまでの発掘を「技術とは言えない」と喝破しているのである。かつて、近所の埋蔵金伝説に、電子ブロックの金属探知器を頼りに闇雲に探そうとしていたワタシなどは、「あぁ、ゴメンナサイ、ゴメンナサイ…」と謝らなくてはならないような勢いなのである。この作者発明者は埋蔵金の探査技術が発達すれば、埋蔵金の発掘は夢や学問でなく産業になるとまで謳いあげるのだった。今さっき、埋蔵金探しは「夢で男のロマンだぁ」と書いたワタシはさらに「ゴメンナサイ、ゴメンナサイ…」と謝らなければならないのである。

　さらに、従来の「埋蔵金探し」を箇条書きに上げ、

• 勘で場所を決めて、縦穴を掘り、さらにいくつもの横穴を掘ったり、ブルトーザーで土を押しのける
• 百年にもわたり、長期間諦めずに掘る

　しかし、そんなミステリー特許に引き込まれていくワタシの心の中のツッコミなど知る由もなく、この埋蔵金小説許では、引き続き具体例を挙げて特許の内容を説明していくことになる。それが、次の「実施例」である。具体的な資料群をもとに、埋蔵金発掘に迫るストーリ〜が書き示されている。

　が、この資料群がスゴイのである。何しろ、こんな感じなのだ。

• 資料A　「常習赤城におよそ三百六十万両。古井戸を掘ることを手がかりとすべし」という水野家に伝わる遺言
• 資料B　「寺の床下から発見された方位図・地図・暗号文書」
• 資料C　「空井戸から発見した銅板と像」
• 資料D　「黄金埋蔵はアッという間にされたらしい、という地元住人のウワサ」

資料Bの一部　「暗号文書」

まさに、歴史ミステリーである

寺の床下から発見された方位図・地図

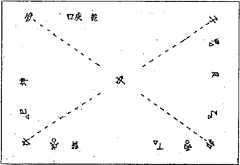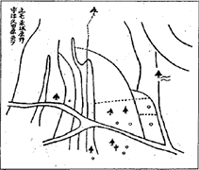　しかも、資料Aの「常習赤城におよそ三百六十万両。古井戸を掘ることを手がかりとすべし」という遺言に対しては、「ここで疑問に思うのは、義父が何故もっと詳しく埋蔵場所を教えなかったのか」などと死者にムチ打ち、マジメなのかそれともツッコミ？と言いたくなるような感想・疑問を書き、この疑問に対して延々２ページに渡り超論理的考察、超心理的考察を加えることで、ついには「埋蔵金は七つの古井戸に埋蔵されたことになる」と、超論理科学的に鉄槌結論を下すのである。

 そして、下に示す「寺の床下から発見された方位図・地図・暗号」を基に、黄金分割を始めとする数学的考察などを駆使し、埋蔵金の位置を推定する。しかも、単に推定するだけでなくて、経済的・効率的に発掘をするために埋蔵金の位置の計算誤差を延々と論じて、ついには誤差50cm〜7m弱だと推定するのであった。なるほど、この歴史ミステリー小説特許は単に技術特許にとどまらず、経済を見据えた経済ミステリー特許でもあったのだ。「埋蔵金の発掘は夢や学問でなく産業になる」のだ。

　さて、この埋蔵金ミステリーで指し示された「埋蔵金の埋まっている七つの古井戸」がどこであるかを知りたい人も多いだろう。ということで、特許の図を重ね合わせ、埋蔵金の埋まっている七つの古井戸の場所をプロットしてみたのが、次の図である。どの辺りか判らない人のために、広域地図をリンクしておくとここら辺りということになる。
 

ここが埋蔵金の埋まっている場所だ

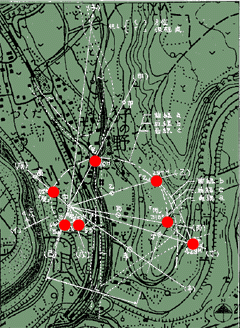　さて、この特許の最後には「なお、この辺りは便利な住宅地向きの環境になりつつあるので、住宅が建設される前に発掘することが望ましい」と
と産業としての指針まで描きつつ筆をおくのである。

　どうだろうか、面白いミステリー小説特許だったのではなかろうか？そして、特許なんて簡単に書ける、と思った人もいるのではないだろうか？そして、どんどん特許を書きたくなる、と思う人も多いに違いない。で、ワタシは思うのだ。できれば、できることであれば、その書いた特許をワタシにも少し分けて頂いて、ワタシのノルマを少しでも減らして欲しい、と強く強く思うのである。