2000-12-17[n年前へ]
■女子大生から見たガンダム 
いいぞぉ、最高だぁ。そういえば、ちゃろん日記の99/10/04の「アレの長さを測るがごとく 」もこんな話だったなぁ。ちなみに私が書いてみたガンダムは女子大生と同程度。ハイ。from J-oの日記。(リンク)(リンク)
2000-12-24[n年前へ]
■A型vB型・大戦争 
血液型分布を眺めてみよう
今年も私の職場には新入社員が入ってきた。その新入社員の中の一人は「血液型+ 動物占い」の信者だった。何しろ、ことあるごとに「血液型 + 動物占いの結果が同じ人はとってもよく似ているんですよ!もうビックリするくらい当てはまるんですよ!もちろん、たま〜に例外の人もありますけど。」といつも私たちに言うのである。もちろん、私も含めてその周囲の人は「その自信と根拠は一体どこからくるんだぁ!」とツッコミを入れるわけであるが、少なくとも本人は気持ち良いくらい自信満々なのである。とはいえ、私も占いというものは「根拠無しにテキト〜に何かを決めつけることができるという素晴らしいもの」だとも思うので、まぁそれはそれで楽しいわけだ。そんな血液型大好きな新入社員なら可愛いものであるが、それがもう少しエラ〜イ人になるとちょっとばかり大変である。私のとなりの部署の部長なども実はそんな血液型信仰者なのであるが、その部の配属には血液型が参考にされるというオソロしくも確かな真実がある(ホントにホント)。そこの某部長曰く「B型は実験が杜撰だから嫌い。」という実に誠実な理由に基づき、その部はA型人間大集合なのである。というよりも、その部からB型は外されているのだ。恐るべき純血追求型人事手法である。ヒットラーもビックリである。
そんなA型人間大集合の部がある一方で、私が所属している部屋(課)は何故かB型が多い。10人強の中で半数程がB型なのである。どこで読んだのか忘れたが、日本人の血液型はA型35%,B型 25%,AB型 10%,O型 30%位であるらしいから、私の課のB型比率はかなり高い。しかし、もちろんそれは単なる偶然だろう。隣の部がB型を排除しているから私の部屋がB型で溢れているのじゃないか、という恐ろしい想像ができないこともないが、そういうわけでもないだろうと私は信じたい。
しかし、「信じたい」という気持ちだけで物事を決めつけるのは危険この上ない。それは「セーラー服の女子高生はみんな可愛くて純真だと信じたい」という危険さと同じくらいデンジャラスである。何事も、先入観で判断してはイケナイのである。確認することが重要なのだ。そこで、今回は「10人強の中で半数程がB型なんていうのはよくある偶然」だということを血液型分布・配置シミュレーション(超手抜き)でも行って確認してみたいと思うのである。そして、私が所属している部屋(課)にB型が多いのがただの偶然であること、つまりある特定の血液型の人間が集まることが不自然ではないことを確認してみたいのである。
さて、今回の血液型分布・配置シミュレーションのやり方は次の通りだ。
- まずは256人の人間を用意する。
- その256人に対して、A型 35%,B型 25%,AB型 10%,O型 30%位になるようにAB型の抗原(AA,AO,BB,BO,AB,OO型)を配置する。
- その後、遺伝子を移動して血液型を再配置する。
- 近所の人間と子供を作る(遠距離恋愛は考えない)。
- 血液型分布・配置を調べる。
この説明の中で、一言で「遺伝子を移動して、近所の人間と子供を作る」と書いたが、もちろんその現象の中には
- 人が引っ越したり・移動したりしていったり、
- 愛が芽生えて子供がデキたり、愛が芽生えないけどデキちゃったりして子供が出来たり、
まぁ、しかしカマキリのようにエッチのあとにメスがオスを食べちゃう動物もいたりするのだし(実際のところは知らないけど)、この恐怖の「子供が一人出現すると親が一人消えてしまう」システムもそんなに不自然ではないのである、ということにしておこう。というわけで、いつもながらの強引な展開だ。
そんなわけで、行ってみた血液型分布・配置シミュレーションの結果が下の動画である。一マス一マスが一人の人間である。時間毎にどんどん血液型分布・配置が変化していく様子が判ると思う。ちなみに、
赤 = A型、緑 = B型、水色 = AB型、紫 = O型である。
 ファイルサイズがデカイのは直すつもり… |
この結果はカラフルにただチカチカするだけの計算結果ではないのである。このチカチカこそが人生の喜怒哀楽なのだ。そこを是非とも心して眺めてもらいたい、と切望する次第である。
じゃぁ、時間を追ってA型、緑 = B型、青色 = O型、紫 = AB型(色が一部さっきと逆転していることに注意)がどう変化していったかというと下の図のような感じだ。それほど一定ではないことがわかるだろう。それぞれの血液型の比率が逆転したりする下克上な瞬間だってままあるのである。
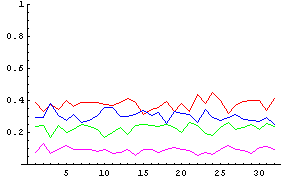 A型、緑 = B型、青色 = O型、紫 = AB型 |
もちろん、これは256人という少ない人数だからこんなに大きく比率が変動するわけである。しかし、今回は「つまりある特定の血液型の人間が集まる」かどうかを調べたいのである。つまり、ある少人数の人間達を考えたときに特定の血液型の比率が多くなることがあるかを調べたいのだから、考える人数は少人数で構わないわけだ。
256人という比較的多い人数を考えた場合ですら、人生のドラマが続く中でそれぞれの血液型比率は結構変化して、それぞれの血液型の比率が逆転したりすることもあるわけだが、じゃぁもっと狭い領域に注目したらどうなるだろうか?例えば、下の瞬間の血液型分布・配置を眺めてみよう。
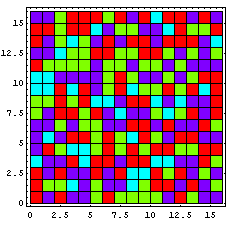 |
おやおや、結構
- A型 = 赤が連続していたり
- B型 = 緑が集まっていたり
- O型 = 紫が多いくせに固まっていたり
- AB型 = 水色が少ないながらも集まっていたり
試しに、先程のシミュレーションである16人(つまり私の部屋(課)の人数位だ)を抽出して調べたときに、A型が一番多かった場合と、一番少なかった場合で、A型の割合だどんなだったかを調べてみたのが次に示すグラフである。ここで、
- 赤 = その瞬間にA型が一番多かったグループにおけるA型の比率
- 青 = その瞬間にA型が一番少なかったグループにおけるA型の比率
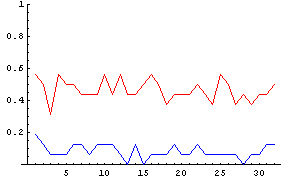 赤 = A型が一番多かったグループにおけるA型の比率 |
なるほど、A型が一番多かったグループではA型の比率が60%を越える時もある。逆にA型が少ないグループでは16人のなかにA型がいない、という状況すらあるのだ。
ということは、私の部屋のB型がほぼ半数という状態だって別に不自然ではなく、それはごく自然なわけだ。もちろん、A型とB型の比率が違うことを考慮しても、全然不自然ではないだろう。ということは、血液型信仰者の某部長による隣の部のB型キライの恐るべき純血追求型人事手法の余波をうけて、私たちの部屋がB型だらけということはなくて、それは単なる偶然だろう、ということがわかるわけだ。
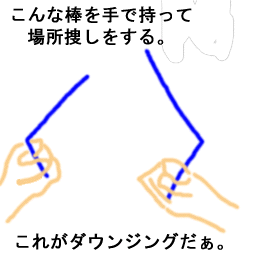
ところで、ここまで書いて「血液型信仰者の某部長」が「ヘンな人」というイメージを持たれてしまうと非常に困る。何故なら、もっと変でなおかつエライ人がイッパイいるのである。(ここでいう「エライ」は関東弁&関西弁のニュアンスだ。つまり、「偉いけど大変な」というニュアンスだ。)血液型信仰者なんてカワイイもんじゃないの、と思えるくらいのスゴサである。だって、ダウジングが超大好きで、奇跡の水が超〜大好きな人だっているのだ。もしかしたら、ダウンジングなんて言葉を知らない人がいるかもしれない。しかし、知らなくて当たり前である。ダウンジングとは下の絵のような棒を持って水脈などの場所捜しをする迷信の中の迷信である。キング・オブ・迷信と言っても良いくらいのアイテムである。
 |
しかも、なんとダウジング&奇跡の水大好き人間が実は某新規材料開発部署の責任者だったりするので、そこらへんは考えると実はかなりコワイものがあるのだが、それはそれ、結構笑える事実(ホントにホント)ので良しということにしておきたい。
2001-03-04[n年前へ]
■柿ピーのシーソー・ゲーム 
柿とピーナツの供給バランスを考える
結婚しようとするカップルが少しばかり気にした方がよいのが、「柿ピーの好み」である。知らない人がいるとは思えないが、念のために書いておこう。柿ピーと言えば、柿ピー= 柿の種 + ピーナッツであって、亀田製菓の大ヒット商品である。そして、何と言ってもビールの安上がりのおつまみだ。
 |
この「安上がりで手軽なおつまみ」というところが、結婚しようとするカップルにはとても重要である。何故なら、結婚する前のカップルであれば洒落た店で飲むことも多いかもしれないが、結婚後はなかなかそうはいかない。いつの間にか手に持ったワイングラスは缶ビール(しかも発泡酒)に変〜身し、「テーブルの上の豪華な食事」はちゃぶ台の上の亀田製菓の柿ピーにバケラッタしているのである。
そうなると、かつては「このソースとても美味しいよね。うふっ。」なんて言っていた二人も変わらざるをえない。そりゃそうだ。柿ピーを目の前にして、気取ってみてもしょうがないわけだ。そんな時、こんな会話に走りがちである。
「柿の種ばっか、食べないでよ!」そう、柿ピーがなまじ「柿の種 + ピーナッツ」なので、片方がどんどん減っていったりすると、これがもう大変。かつては、ワインを片手に愛を語らっていた二人も、今やビール(しかも実は発泡酒)を片手に食い物の奪い合いをすることになるのである。
「オマエこそ、ピーナッツどんどん食えよ!」
これが、カップルの二人がとても似たもの同士で、「私達二人とも柿の種がスゴ〜ク好きだから、ピーナッツなんかいらないの。だから、- 柿の種だけが100%入った柿の種 - を買うの!」なんて感じなら、もちろんノープロブレムだろうし、あるいは、「ぼくらは、ピーナッツだけを買うのさ!」という感じのカップルでも同様だろう。
 |
あるいは、もう「ぼくは柿の種が好きだけど、きみはピーナッツが好き。二人は違っているから良い組み合わせなのさ。柿の種はぼくがどんどん食べるから、君はピーナッツをお食べ」なんてカップルでもいいだろう。こちらも、「ひとまずは」ノープロブレムである。つまりは、全く同じが正反対のカップルであれば、大抵の場合ほとんど問題はないのである。
しかし、「柿ピーは柿の種とピーナッツが適当な割合で入っているから良いのさ」なんていうグルメ気取りのカップルがいたりすると、大変である。
「アンタの食べる割合、少しおかしくない?」となるのは必至である。この数分後には、巨人の星の一徹父ちゃんのごとく、ちゃぶ台はひっくり返されているのに違いないのである。柿ピーの割合恐るべしだ。
「何言ってんだよ!オマエの方が柿ピー食べ過ぎだってんだよ!」
「そんなことないわよ!」
そして、しかもこれが理系カップルともなれば、もう最低だ。
「柿とピーの割合は7:3で食べなさいよ!」という具合になるに決まっているのだ。このままいくと、柿ピーを前にして離婚談義にもなりかねない。なんともオソロシイ話である。(* ピー柿は7:3でピーナツの方が多い。そんなのが実在することが私にとっては驚きである。)
「違うだろ、6:4が適正値に決まってるだろ!」
「そんなにピーナッツを食べたいなら、柿ピーじゃなくてピー柿*にしなさいよ!」
「別にピーナッツが過半数を超えるほどがイイって言ってんじゃねぇ〜!」
「何よ、もっと定量的に話しなさいよ!」
そういうわけで、「柿ピーの好み」「柿ピーの割合」「柿ピーの消費の割合」なんていうものは、結構結婚しようとするカップルには重要なのである。結婚しようとするカップルはぜひとも心して聞いておいてもらいたい。とはいえ、モテモテ度テストで
「女にモテない、というより、女に興味がないオマエ。今、一番気になることがドリキャスの値下げだったりなんかしない? まーそれも人生だけど、モテたほうがおいしいことは多いぜ? もうちょい女に関心持てよ。」と判定された私が言っても説得力がないか。
ところで、そもそも柿ピーの割合はどのくらいが普通なのだろうか?WEBで検索してみると、柿ピー10に対して
- 柿の種 : 7〜6
- ピーナッツ : 3〜4
そこで、試しに私も手元にあった小袋入り亀田の柿ピーの中身を調べてみた。調べたのは「小袋入り亀田の柿ピー」である。
 |
この一袋の中身を開けてみると大体こんな感じである。
 |
もちろん、単に数えても良いわけではあるが、「クダラナイことに、無意味なほどに大ゲサな道具を使うのがこのサイトのポリシー」でもあったりするので、まずは画像処理ソフトを使って柿の種とピーナッツの個数をカウントしてみた。使ったソフトはUTHSCSAImageTool である。PCベースでフリーでお手軽で粒子カウントとなるとこのソフトになるだろう。もちろんNIH-imageベースのScionImagePCという選択肢もないわけではないが、こと粒子カウントになるとはるかにImageToolの方が使いやすい。マクロの取っつきやすさ(機能は較べものにならないほどおちるが)もNIH-image系よりも上である。
さて、まずは上の画面内で柿の種を粒子カウントしてみたのが次の画面だ。この画面では見つかった柿の種は赤い縁取りがされ、個数がマーキングされていることがわかると思う。ちなみに、この画面内では93個の柿の種が見つかった。しつこいようだが、「数えた方が早いだろっ!」というツッコミはこの「できるかな?」では厳禁である。
 |
同じようにして、ピーナッツをカウントしてみたのが次の画面である。この画面では、ピーナッツは23個見つかった。
 |
すると、個数ベースでピーナッツが23/(93+23) = 20%で、残りが柿の種で80%ということになる。柿ピーの割合は大体8:2であったことになる。確か、WEBの亀田製菓に関する情報では
「柿ピー」のブレンドは、柿の種6に対してピーナッツ4が基本と書いてあったような気がするので、今回の8:2というデータは測定誤差、とその他の何らかの誤差が重なったものだろう。いや、そんな誤差はどうでも良いか。
ところで、大きな袋に入った柿ピーを食べながらよく考えることがある。私は柿の種が大好きなので、柿の種ばっかり選んで食べていくと、袋の口近くの上の方にはピーナッツばかりが残り、明らかに袋の場所ごとに柿の種とピーナッツの割合が異なってしまっていることがよくある。この柿の種とピーナッツの割合の時間的・空間的変化は一体どうなっているものだろうか?そこで、今回その「ピーナッツの柿ピーに占める割合の時間・空間的変化」について、少し考えてみることにした。
まずは簡単に判るように、袋の中から均等に柿の種とピーナッツを「柿ピーの割合を適当な割合で」食べていった場合、「ピーナッツの柿ピーに占める割合」は次の図のようになる。この図は横軸が時間で、縦軸がピーナッツの柿ピーに占める割合である。
緑 : 柿ピーを8:3の割合で食べた場合  |
今回の場合柿ピーは8:2で入っているので、青の場合のように柿ピーを8:2の割合で食べていくと、時間にして10分後に柿ピーがなくなるまで、ピーナッツの柿ピーに占める割合は20%をキープしたままである。しかし、(少しばかりピーナッツが好きな人が)柿ピーを8:3の割合で食べてしまうと、つまりピーナッツを過剰に食べてしまうと、どんどんピーナッツの割合は減ってしまい、ついに8分経過後にはピーナッツが袋の中から無くなってしまうのである。つまり、あとの2分は悲しみと共に柿の種を食べ続けなければならないのである(私は柿の種が好きなので悲しくもなんともないが)。
じゃぁ、袋の中の空間的分布も考えてみたらどうなるか、というのを次に計算してみた。まずは、袋を大きく二つに分けて、袋の入り口で適当な割合で柿ピーを食べた後、袋の奥から袋の入り口の方へ柿ピーを持ってくる。また、その際に適度に柿ピーをかき混ぜる。そして、柿ピーがなくなるまで柿ピーの割合の変化を調べてみるのである。ちなみに、IE4以降+Excel2000以降?の人であれば、ここをクリックすれば、その計算シートで遊ぶことができると思う。
例えば、「柿ピーを8:2の割合で食べた場合」と「柿ピーを8:5の割合で食べた場合」のピーナッツの柿ピーに占める割合の時間・空間的変化を調べてみたのが、次に示す結果である。ちなみに、このいずれも横軸は時間である。また、時間軸にして30前後の時点で柿ピーは完全になくなっている。
 ちょっと計算上の誤差が大きいが、それはちょっと無視してもらいたい。 |
さて、左の「柿ピーを8:2の割合で食べた場合」、つまり本来の柿ピー比と同じ割合で食べていった場合には、入り口近くでも奥の方でも柿ピーの比率は変わらない。そして、入り口の方から柿ピーを取った分を、奥の方から補給しているので、奥の方では時間軸20の時点で空になってしまっている。左の図でピーナツの割合がゼロになっているように見えるのは、実は単に柿ピーがなくなっただけなのである。そして、入り口近くの柿ピーが時間軸30の時点で空になっているまで、柿ピーの比率は変わることはない。当たり前だ。
では、「柿ピーを8:5の割合で食べた場合」はどうだろうか?つまり、本来の割合よりもピーナッツを多く食べがちな人の場合だ。そんな場合の右を見てみると、奥の方は単に入り口近くに柿ピーを補給しているだけなので、柿ピーの割合は変わらないままだ。しかし、入り口近くではあっという間にピーナッツの割合が減ってしまっている。ほとんどなくなっている、といっても良いくらいの状態である。つまり、ピーナッツ大好き人間にとっては、手の届く袋の入り口近くには全然ピーナッツがないという、拷問状態なのである。周りに女子校や共学の学校はあるけど、自分の通う学校が男子校だったみたいなキツイ状態である。ちなみに、私は高校時代に私服の共学の学校に通った結果、制服の女子高生に強い強い憧れを抱くに至ったことを否定できなかったりするのである。
話を戻して、それでは「袋を適当にかき混ぜながら」、「柿ピーを8:5の割合で食べた場合」はどうなるだろうか?というのが次の結果である。こうすると、奥の方のピーナッツもどんどん消費されているのがわかる。入り口近くも奥の方も、同じようにどんどんピーナッツの割合がどんどん減ってしまい、時間軸15の時点で完全になくなってしまっている。あとは柿の種がなくなる時間軸30の時点まではもう柿の種と向かい合うだけの人生なのである。ツラすぎる(ピーナッツ好きの人にとっては)。私の知人のオッパイ星人が結婚後に妻から、
*一部、不適当な発言がありましたことをお詫びします。
 |
つまりは、ピーナッツが食べたいからといって、あまり柿ピーの袋をかき混ぜるのは良くないということなのである。もちろん、短期的にはピーナッツがたくさん食べることができて良いわけであるが、長期的に見ればその後の長い「柿の種人生」が待っているのである。それが端的にわかるのが、次の「ピーナッツをどれだけ食べているか」を示す結果である。
この結果の中で、上の方に示した「柿ピーの袋をかき混ぜない場合」では、結構最後までピーナッツを細々と食べていけることがわかるだろう。柿ピーがなくなるのが時間軸で30前後の時点であるが、その少し前23位の時点までピーナッツを食べていけるのである。それに対して、ピーナッツを早く食べたいばかりに、柿ピーの袋をかき混ぜまくりの下の「柿ピーの袋をかき混ぜた場合」には、時間軸で13前後の時点でもうピーナッツがなくなってしまっている。もう、コイツには「柿の種人生」しか残されていないのである。
| 柿ピーの袋をかき混ぜない場合
結構最後までピーナッツを細々と食べていける |
| 柿ピーの袋をかき混ぜた場合
なんとも、太く短くのピーナッツの食べ方である… |
とはいえ、柿ピーの袋をかき混ぜながら太く短くピーナッツを食べるか、それをじっとガマンの子で細々と最後までピーナッツを食べるか、どっちが良いかは難しいところだ。ちなみに、私はかき混ぜまくりで柿の種を食いまくり、残ったピーナッツは人にプレゼントするというとても良い性格である。だったら、100%柿の種を買えって感じであるが、売店には置いてないことも多いから、しょうがないのである。
というわけで、今回はビール(やっぱりあくまで発泡酒)を左手にそして柿ピーを右手でつまみながら、酔っぱらった頭で(いつものことだが)、ツマラナイことを考えてみた。モノが本当の柿の種であればオチて芽が出るのが普通なのだけれど、今回の柿ピーの話はオチがあるわけでも芽が出るわけでもない。酔っぱらいのタワゴトだから意味なんか全然ないのである。と、日記には書いておこう(意味不明)。
2001-04-07[n年前へ]
■スカートの力学 予習編 
風に吹かれるスカートは
四月になって、春風が強く吹き始めた。春風と言えば聞こえは良いけれど、コンタクトレンズを使っていたりする人は強い風が吹くとゴミが入ったりしやすくて辛いだろうし、まして花粉症だったりすると涙が止まらなかったりしてきっと辛いことだろう。そんな辛い季節でも、たまにドキドキするような気持ちになる瞬間がある。もちろん、それは春風にスカートが舞い上がった瞬間だ。スカートが風に吹かれた瞬間に、私は理由もなく(いや理由はちゃんとあるのだが)心と体がドキドキする。それはもちろん私だけでなくて、男なら間違いなく誰しもがそんなドキドキを味わったことがあるはずだ。もっとも、そんな男心を理解しないヤカラはそんなドキドキを軽蔑するに違いないのだが、それが男というものなのだからしょうがないのである。
とはいえ、男心は「男の心」という位だから、女性にはなかなか判りづらいことだろう。「女子高生なんかはどうせスカートの下に短パンを履いているのに、それでもドキドキするものなの?」などと言う女性も多い。しかし、「それでもドキドキしたりする」ものなのである。いや、もちろんスカートの下にジャージを履いてるなんてもっての他ではあるが、短パンくらいならドキドキ度は全然減らないものなのである。それが、つまりは男というものなのだ。
そして、逆に「スクール水着の秘密」ではないが、女性には常識でも我々男には全然判らないことが世の中にはたくさんあるに違いない。ちなみに、私にとってはスカートもその一つである。何しろ、あまりスカートについて自分のこととして考える機会がなかったのである。いや、実際のところそんな機会は全然無かったのである。そこで、今回は「春風に吹かれるスカート」について考えてみることにした。(本題に入る前に一応書いて置くけれど、今回も「スクール水着の秘密」と同じく、女性から見たら「なんて当たり前のことを」とか「それちょっと違うんじゃないの」ということを書いている。そんな風に感じた方は是非、メールででも私に情報でも頂けたら、と思う次第である。)
| さて、本題である。 この右の図のような「風に吹かれながら女性がスカートを押さえている風景」をよく見かける。もっとも、「よく」見かけるなんていうと、私がさぞそういう風景を探し求めているように聞こえるかもしれないが、そんなことはない。風が強い季節であれば、そんな風景は満ちあふれているのである。 さて、この女性のスカートのように風に吹かれたスカートについてちょっと考えてみよう。
| 女性がスカートを押さえている風景」 (animeBODY)  |
まずは、体の前方から強い風が吹いているものとする。つまり、強い向かい風が吹いている状態である。ちょっとその女性にとってはツライ状態である。そこで、うすみどり色のスカートを履いている女性は、スカートがめくれ上がらないように、スカートの前部を両手で膝近くで押さえているわけだ。しかし、それでも風に吹かれてスカートの後ろは舞い上がってしまう。例えば、下の右図で女子高生の体の後ろでスカートがめくれ上がっている。それをもっと単純にしたのが左で、この図中ではスカートはCの位置まで上がってしまっている。
 |  M.H.Tさん画 |
もちろん、男心からすればCどころではなくて、Aくらいまでスカートには高く高く舞い上がって欲しいわけであるが、女心からすればそれはとんでもない話だろう。
さて、このスカートのめくれあがる位置Cは何で決まるだろうか?もちろん、流体力学・弾塑性体力学などを総動員して解かなければならないわけではあるが、それは次回以降のお楽しみということにしておいて、予習編の今回は単純にスカートがOC方向には曲がらないものとしてみよう。だとしたら、話は簡単だ。ただスカートの裾の広さでCBの長さは制限されるわけである。スカートの裾が広ければ、スカートの端は高くまでめくれあがってしまうし、スカートの裾が狭くなっていれば、スカートは比較的低いところまでしかめくれない。
だから、この下の色々なスカートの中でプリーツ・スカートのようなフレアタイプの場合は、スカートは高隈でめくれ上がってしまうだろうし、タイトスカートのようなスカートの裾が狭いものであれば、強い風にも負けず、スカートはめくれ上がることはないだろう。
プリーツ・スカート
|
|
|
|
しかし、しかしである、スカートの裾を狭くすれば春風にスカートが舞い上がってしまうことはなくなるかもしれない。だけど、スカートの裾の長さが制限するのはスカート自身だけでない。スカートを履いている女性の動き自体も制限してしまうのである。それではずいぶんと窮屈になってしまうことだろう。スカートの裾が狭いせいで歩幅も狭くなって、走り回ったりすることもできなくなるに違いない。だからこそ、脚を蹴り上げる藤原紀香のJ-PHONECMのスカートも、脚の動きが制限されないように、スカートの後ろに切れ目が入っているのだろう。
ということは自由に駆け回ったりしようとすると、つまり、スカートが足枷にならないような裾の広いスカートを履いていると、そんなスカートは風に吹かれて舞い上がりやすいわけだ。そして、そんなスカートを履いていると春風に困らせられることになる。
とはいえ、実際にスカートを履いたことがあるわけじゃないから、私には実際のところよく判らない。だから、女性の方々の「本当はこうなのだ」という教えでも請うしかないのである。結局、スカートの話は、スカートを履く人には常識きわまりない話だろうが、私はこれまで考えたこともなかったので全然よくわからない。これが、男と女の常識の違いなのかもしれない。いや、単に私の常識知らず、という可能性が一番大ではあるのだけれど…
そういえば、辞書でskirtを引いてみると「女;女の子」なんていう風にも書いてあった。なるほど、風に吹かれるスカートも走り回るスカートも、確かにその女性そのものなのかもしれないなぁ、と少しばかり思ったりしたのである。だとしたら、風に吹かれるスカートは向かい風には負けないで欲しいな、と柄にもなく思ってみたりするのである。ホントに私の柄じゃないのだけれど。
2002-01-20[n年前へ]
■徳川埋蔵金殺人事件 
超論理特許ミステリー「狩野埋蔵金の埋蔵場所を解読し発掘する方法」
ワタシの勤務先では「一年に*本特許を書くべし」という恐ろしいノルマがある。もちろん、こまめに書いていれば何の問題もないのだけれど、他の仕事にかまけてついつい後回しにしていたりすると、年末や期末には特許をまとめて書かなければならなくなる。架空の物語を量産する小説家のように、架空の実験データを描き整理し、架空の特許を量産しなければならなくなるのである。
いつものごとく、昨年末もそうだった。年末の最後の二三日は特許書きで追いつめられ、しかも書き上げられずに、できの悪い小学生のように、家へ書きかけの特許を持ち帰って、正月休みに特許を書かなければならなくなったりしていたのである。そんなわけで、正月番組を見ながら、特許庁の電子図書館のサイトにアクセスし特許調査をしつつ特許を書いていた。が、正月番組などを眺めているせいか、どうにもマジメに特許が書けなかったりするのである。いつしか、ビールを飲みながら仕事とは全然関係無い特許公報を眺めていたりしたのである。
今回、紹介する特開2001-42765「狩野埋蔵金の埋蔵場所を解読し発掘する方法」という公開特許公報もその一つである。キャッチーな名前で想像つくとは思うが、なんとこの特許出願はいわゆる赤城山徳川埋蔵金の場所を発掘するための特許なのである。世に出される特許は数多く、埋め立てゴミの数より多いくらいかもしれないが、そんな中でも「埋蔵金の隠し場所を解読し発掘する方法」なんて特許は見たことがない。歴史ミステリー、暗号ミステリー、そして、ご当地モノミステリーなどが好きなワタシは思わず目を奪われ、その特許を読み始め、そしてこの超論理特許ミステリーの世界に引き込まれたのだった。
そして、この特許のあまりの素晴らしさに今回こんな感想文を書いて、世の中にこの超論理特許ミステリー特許を広めたいと思うのである。そして、さらにはこの感想文を読んだ人が特許フォーマットに慣れ親しみスラスラと特許を書けるようになり、ワタシのように特許を書き残しで苦しむ人が減ることを強く望む次第なのである。
さて、特許では、まず「発明の名称」を書かなければならない。この特許でももちろんそうだ。というわけで、
「発明の名称」 狩野埋蔵金の埋蔵場所を解読し発掘する方法
何とも、キャッチーな名前である。これが火曜サスペンス劇場であれば、「徳川赤城山埋蔵金全裸殺人事件2 湯けむり露天風呂で美人女子大生が消えた!村に残る伝説が不気味に今よみがえる!」くらいにはパワーアップすることだろうが、特許の書類としては十分に魅力的である。この名前を見れば、誰しもワタシのようにこの特許の世界に引き込まれるハズである。
そして、次に「どんな範囲のこと」を特許として宣言するかを書くわけだ。これを請求項と呼ぶが、この特許はもちろんこれだ。
「請求項」 従来一般に赤城山徳川埋蔵金といわれている黄金の埋蔵場所を発見・発掘すること
なんと、赤城山徳川埋蔵金といわれている黄金の埋蔵場所を発見・発掘してしまうのである。特許を書いて大金を手に入れるという話はたまに聞くが、特許を書いて埋蔵金を手に入れるという話は聞いたことがない。まさに、夢というか、男のロマンというか素晴らしい特許なのである。
そして、次に「従来の技術」というセクションが続く。つまり、従来はこんな問題がありますよ、こんなに不便だったのですよ、ということを書くのである。それに対して、今回書いたこの技術はそんな「従来の課題」を解決できて、価値があるのですよ、と訴えるのだ。そこで、この特許は説く、
「従来の技術」 従来の技術は、解読に科学性が不足していたために、経済効果の悪いものであった。…暗号のかたちで示されている埋蔵金を資源として再利用するためには、闇雲に探したのでは経済的に成り立たないので技術とは言えない。埋蔵金の探査技術が発達すれば、埋蔵金の発掘は夢や学問でなく産業になるであろう
なんと、これまでの発掘を「技術とは言えない」と喝破しているのである。かつて、近所の埋蔵金伝説に、電子ブロックの金属探知器を頼りに闇雲に探そうとしていたワタシなどは、「あぁ、ゴメンナサイ、ゴメンナサイ…」と謝らなくてはならないような勢いなのである。この作者発明者は埋蔵金の探査技術が発達すれば、埋蔵金の発掘は夢や学問でなく産業になるとまで謳いあげるのだった。今さっき、埋蔵金探しは「夢で男のロマンだぁ」と書いたワタシはさらに「ゴメンナサイ、ゴメンナサイ…」と謝らなければならないのである。
さらに、従来の「埋蔵金探し」を箇条書きに上げ、
- 勘で場所を決めて、縦穴を掘り、さらにいくつもの横穴を掘ったり、ブルトーザーで土を押しのける
- 百年にもわたり、長期間諦めずに掘る
しかし、そんなミステリー特許に引き込まれていくワタシの心の中のツッコミなど知る由もなく、この埋蔵金小説許では、引き続き具体例を挙げて特許の内容を説明していくことになる。それが、次の「実施例」である。具体的な資料群をもとに、埋蔵金発掘に迫るストーリ〜が書き示されている。
が、この資料群がスゴイのである。何しろ、こんな感じなのだ。
- 資料A 「常習赤城におよそ三百六十万両。古井戸を掘ることを手がかりとすべし」という水野家に伝わる遺言
- 資料B 「寺の床下から発見された方位図・地図・暗号文書」
- 資料C 「空井戸から発見した銅板と像」
- 資料D 「黄金埋蔵はアッという間にされたらしい、という地元住人のウワサ」
 |
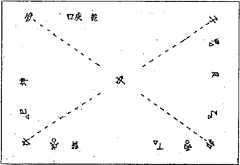 |  |
しかも、資料Aの「常習赤城におよそ三百六十万両。古井戸を掘ることを手がかりとすべし」という遺言に対しては、「ここで疑問に思うのは、義父が何故もっと詳しく埋蔵場所を教えなかったのか」などと死者にムチ打ち、マジメなのかそれともツッコミ?と言いたくなるような感想・疑問を書き、この疑問に対して延々2ページに渡り超論理的考察、超心理的考察を加えることで、ついには「埋蔵金は七つの古井戸に埋蔵されたことになる」と、超論理科学的に鉄槌結論を下すのである。
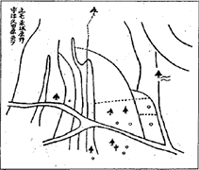
そして、下に示す「寺の床下から発見された方位図・地図・暗号」を基に、黄金分割を始めとする数学的考察などを駆使し、埋蔵金の位置を推定する。しかも、単に推定するだけでなくて、経済的・効率的に発掘をするために埋蔵金の位置の計算誤差を延々と論じて、ついには誤差50cm〜7m弱だと推定するのであった。なるほど、この歴史ミステリー小説特許は単に技術特許にとどまらず、経済を見据えた経済ミステリー特許でもあったのだ。「埋蔵金の発掘は夢や学問でなく産業になる」のだ。
さて、この埋蔵金ミステリーで指し示された「埋蔵金の埋まっている七つの古井戸」がどこであるかを知りたい人も多いだろう。ということで、特許の図を重ね合わせ、埋蔵金の埋まっている七つの古井戸の場所をプロットしてみたのが、次の図である。どの辺りか判らない人のために、広域地図をリンクしておくとここら辺りということになる。
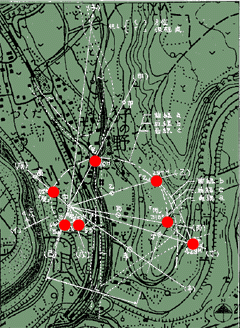 |
さて、この特許の最後には「なお、この辺りは便利な住宅地向きの環境になりつつあるので、住宅が建設される前に発掘することが望ましい」と
と産業としての指針まで描きつつ筆をおくのである。
どうだろうか、面白いミステリー小説特許だったのではなかろうか?そして、特許なんて簡単に書ける、と思った人もいるのではないだろうか?そして、どんどん特許を書きたくなる、と思う人も多いに違いない。で、ワタシは思うのだ。できれば、できることであれば、その書いた特許をワタシにも少し分けて頂いて、ワタシのノルマを少しでも減らして欲しい、と強く強く思うのである。





