hirax.net::Keywords::「小説」のブログ

■今日の加納朋子 「月曜日の水玉模様」の文庫本　

　図書コーナーで「月曜日の水玉模様」の文庫本を買った。ハードカバーを持っているにも関わらず買ったのは、解説をじっくり読みたいから。
　「日常の謎」ミステリーが好きな人にとって、「解説」というのはこれもまたミステリーの謎解きそのものだと思う。自分が眺めていた小説の中の景色を「ほぅら、こんな見方もあるでしょう？」と解説が書くことで、その景色をまた違った場所から眺めたストーリーを描くのだから。
　でもって、この本の中の「毎日、乗り降りを繰り返す通勤電車の中で出会う、数百、数千の人達。彼らの一人一人はいったいどういう暮らしをし、何を考え、どこへ向かっているのだろう？」なんて加納朋子らしくて良いなぁ。瞬間写真コレクションも思わず連想してしまう。　

■日曜日の雨天決行　

　今日の「月曜日の水玉模様」。それまでの登場人物達が、選手として「審判」として応援団として、全員集合する最終話「日曜日の雨天決行」なんか良いなぁ。小説の中でまで後味を悪くはしたくない、ってのが加納朋子の甘い味だもの。
　審判を交代する時の「一言二言親しげに言葉を交わして」なんて、あっさりがまた良いなぁ。こういうところをまさか読み飛ばしたりする人はいないとは思うが…。

■私と二度めに出会う「水」　

クリスマスの小さな遺品

　先日、こんなメールを頂いた。

　私の娘は小学三年生。図書館から借りてきた「水の一生」といった、子供向け科学本（蛇口から出た水は下水を通って…<途中大幅に省略>…再度雨になって…というヤツです）を読んでおりました。そこで彼女はいくつかの疑問を口にしました。

「一度下水に流した水は、どのくらい経ったらまた私のところへ戻ってくるの？」
 

私　「必ずしもすべての水が海まで行くわけではなくて、下水処理場で蒸発して、川の取水口あたりで雨になる分子もあるはずだから、そうだなあ、一番早くて３日くらいかなあ。　勿論もっと長い場合もあるし、一度流したらキミが生きている間にはここには戻ってこない分子もあると思うよ」

「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」

私　「う〜ん…　　どれくらいなんだろう？」

　さて、どう思われますか？

　ところで、この後半の疑問「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」というのはたまに見かける話である。何かの小説で、「このコップの話が主人公が科学を志したきっかけになっている」という小道具に使われている例も読んだことがあるような気がする。

　たまに見かける話ではあるのだけれど、同じ本を読んでも人それぞれ抱く感想は違うし、私なりにも考えてみたい気もしたので、今回はこの「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」を考えてみることにした。

　人が一日に「出会う」水はどの位の量だろうか？成人男子が安静にした状態で、一日当たり大体2.5リットルの水を消費するという。すると、小さい子供の場合でも、少なくとも一日2リットルくらいは水を消費する、つまり水と「出会って」そして「分かれる」ことになる。2リットルの水というと、2000gだから、これを水の1molあたりの重さ18g /molで割って、さらにアボガドロ数（1mol当たりの分子数）をかけてやると、(2l = 2000g ) / 18g x 6.022x10²³個 = 6.7 x 10²⁵個となり、私たちが一日に出会う水分子の数の個数がわかる。

　この「とある一日に私たちが出会った水」が川へ流れて、海へ流れて、地球上にまんべんなく拡がったとしよう。地球上の限りなくある水の中に含まれる「とある一日に私たちが出会った水分子」の割合は、いったいどのくらいの程度になるのだろうか？

　地球上の水は大体14億km³くらいだという。そのほとんどは96.5%は海水で、残りが陸地のさまざまな場所（そしてわずかに空気中）に存在している。この地球上にある水の重さを計算すると、14億km³= 1350000000km³ = 1.4 x 10⁹ x 10¹² kg= 1.4 x 10²⁴ g ということになって、これを水の1molあたりの重さ18g /molで割ってやると、地球上に存在する水分子の総量は 1.4 x 10²⁴/ 18 = 7.8 x 10²²mol ということになる。mol数から水分子の量に直すために、アボガドロ数6.022x10²³個/molをかけてやると、地球上の水分子の総量= 4.5 x 10⁴⁶ 個という数字が得られる。

　すると、地球上の限りなくある水の中に含まれる「とある一日に私たちが出会った水分子」の割合は
「とある一日に私たちが出会った水分子」 / 地球上の水分子の総量 = 6.7x 10²⁵個 / 4.5 x 10⁴⁶ 個 = 1.5 x 10^-21= 0.00000000000000000015%というとても小さい割合になる。この割合は、新たに水分子と出会った時に、その水分子が「とある一日に私たちが出会った水」である確率と言い換えても良いだろう。とにかく、私たちの普段の生活の感覚からすれば、限りなく小さく思えてしまう。しかし、その再会の確率はとても小さく思えてしまうのだけれど、決して私たちは「とある一日に私たちが出会った水分子二度と水と再会しない」わけでは無いのである。

　例えば、180mlのコップ一杯の水の中には( 180ml = 180g ) / 18g x 6.022x10²³個= 6.0 x 10²⁴個の水分子が含まれている。ということは、このコップ一杯に含まれる水分子の中にいる、かつて「とある一日に私たちが出会った水分子」の数を計算してみると、
コップ一杯に含まれる水分子の数 x 「とある一日に私たちが出会った水」である確率= 6.0 x 10²⁴個 x 1.5 x 10^-21  = 9000個ということになる。コップ一杯の水の中にはかつて「とある一日に私たちが出会った水」が一万個近くも存在していることになる。

　しかも、この計算は「とある一日に私たちが出会った水分子」だけで計算していて、決して「これまでに私たちが出会った水分子」で計算しているわけではないのだから、「コップ一杯の水の中で、私と２度目に出会う水」はもっと多いことになる。もちろん、実際には私たちが消費した水が理想的に拡散したりはしないだろうから、こんな風に上手くはいかないだろうけれども。

　とりあえず、「コップ一杯の水の中で、私と２度目に出会う水はどれくらいあるの？」という疑問を口にした小学校三年生の娘さんには、「ずっと昔のある日に出会った水がコップ一杯の中には一万個近くもあるかもね」と答えておくのが良いかもしれない。計算の中身、アボガドロ数なんて言っても、小学校三年生では「あぼがど？あぼがろど…？」と頭がこんがらがるだけかもしれないけれど、とりあえず「おとーさんって、何でもわかるんだー」とちょっとくらいは尊敬されたりするかもしれない。
 

　そういえば、先日東京で初雪が降った。「雪は天から送られた手紙」とは中谷宇吉郎の残した名言だけど、その雪を見ながらこんなことを考えた。

　ある日誰かが亡くなり、荼毘に付される。すると、その人の体のほとんどの部分は火と共に空へ昇っていくことだろう。成人の体のおよそ60%は水分だから、体重60kgの人であれば、その60%の36000gもの水が空へ還ってゆくことになる。その空へ還っていった水分子が世界中に散らばっていった後に、いつかまたその水分子と出会うためにはどの程度の水があれば良いだろうか？どの程度の水があれば、この中には「かつてあの人と共に空に帰っていった水分子」が一個くらいはある、と言えるものだろうか？

　これを先程と同じように計算してみると、ほんのちょっと「1 x 10^-3g」ほどの水があれば、その中には「かつてあの人と共に空に帰っていった水分子」が一個くらいある、という結果になる。「1x 10^-3g」ということは、大きさで言うと1mm³ほどになる。ちょうど雨粒一滴と同じ位の大きさだ。空から降ってくる雨一粒の中には「かつて亡くなった人と共に空に帰っていった水分子」が１個が漂っている、ということになる。

　冬の雪の一片の大きさが雨の一粒と同じくらいであるかは判らないけれど、今日のように何時の間にか雨が雪に変わることもあるくらいだから、やっぱり雪も雨と同じような大きさなのだろう。だとすれば、空から降ってくる雪の一片の中には、「かつて亡くなった人と共に空に帰っていった水分子」が１個宝石のように入っていてもおかしくはない。「雪は天から送られた手紙」であるならば、その中にはその手紙を天から送ってくる「かつて亡くなった人」のまるで遺品が１個づつ封じ込められているのである。「雪は天からの遺品」と言っても良いかもしれない。

　間もなく、クリスマス。そして、クリスマスには白い雪が付き物だ。空から舞い降りてくる白い雪の中には大切な１個の水分子「クリスマスの小さな遺品」が入っているのである。

■徳川埋蔵金殺人事件　

超論理特許ミステリー「狩野埋蔵金の埋蔵場所を解読し発掘する方法」

　ワタシの勤務先では「一年に＊本特許を書くべし」という恐ろしいノルマがある。もちろん、こまめに書いていれば何の問題もないのだけれど、他の仕事にかまけてついつい後回しにしていたりすると、年末や期末には特許をまとめて書かなければならなくなる。架空の物語を量産する小説家のように、架空の実験データを描き整理し、架空の特許を量産しなければならなくなるのである。

　いつものごとく、昨年末もそうだった。年末の最後の二三日は特許書きで追いつめられ、しかも書き上げられずに、できの悪い小学生のように、家へ書きかけの特許を持ち帰って、正月休みに特許を書かなければならなくなったりしていたのである。そんなわけで、正月番組を見ながら、特許庁の電子図書館のサイトにアクセスし特許調査をしつつ特許を書いていた。が、正月番組などを眺めているせいか、どうにもマジメに特許が書けなかったりするのである。いつしか、ビールを飲みながら仕事とは全然関係無い特許公報を眺めていたりしたのである。

　今回、紹介する特開2001-42765「狩野埋蔵金の埋蔵場所を解読し発掘する方法」という公開特許公報もその一つである。キャッチーな名前で想像つくとは思うが、なんとこの特許出願はいわゆる赤城山徳川埋蔵金の場所を発掘するための特許なのである。世に出される特許は数多く、埋め立てゴミの数より多いくらいかもしれないが、そんな中でも「埋蔵金の隠し場所を解読し発掘する方法」なんて特許は見たことがない。歴史ミステリー、暗号ミステリー、そして、ご当地モノミステリーなどが好きなワタシは思わず目を奪われ、その特許を読み始め、そしてこの超論理特許ミステリーの世界に引き込まれたのだった。

　そして、この特許のあまりの素晴らしさに今回こんな感想文を書いて、世の中にこの超論理特許ミステリー特許を広めたいと思うのである。そして、さらにはこの感想文を読んだ人が特許フォーマットに慣れ親しみスラスラと特許を書けるようになり、ワタシのように特許を書き残しで苦しむ人が減ることを強く望む次第なのである。
 

　さて、特許では、まず「発明の名称」を書かなければならない。この特許でももちろんそうだ。というわけで、
「発明の名称」　狩野埋蔵金の埋蔵場所を解読し発掘する方法
　
　何とも、キャッチーな名前である。これが火曜サスペンス劇場であれば、「徳川赤城山埋蔵金全裸殺人事件２ 湯けむり露天風呂で美人女子大生が消えた！村に残る伝説が不気味に今よみがえる！」くらいにはパワーアップすることだろうが、特許の書類としては十分に魅力的である。この名前を見れば、誰しもワタシのようにこの特許の世界に引き込まれるハズである。

　そして、次に「どんな範囲のこと」を特許として宣言するかを書くわけだ。これを請求項と呼ぶが、この特許はもちろんこれだ。
「請求項」　従来一般に赤城山徳川埋蔵金といわれている黄金の埋蔵場所を発見・発掘すること

　なんと、赤城山徳川埋蔵金といわれている黄金の埋蔵場所を発見・発掘してしまうのである。特許を書いて大金を手に入れるという話はたまに聞くが、特許を書いて埋蔵金を手に入れるという話は聞いたことがない。まさに、夢というか、男のロマンというか素晴らしい特許なのである。

　そして、次に「従来の技術」というセクションが続く。つまり、従来はこんな問題がありますよ、こんなに不便だったのですよ、ということを書くのである。それに対して、今回書いたこの技術はそんな「従来の課題」を解決できて、価値があるのですよ、と訴えるのだ。そこで、この特許は説く、

「従来の技術」　従来の技術は、解読に科学性が不足していたために、経済効果の悪いものであった。…暗号のかたちで示されている埋蔵金を資源として再利用するためには、闇雲に探したのでは経済的に成り立たないので技術とは言えない。埋蔵金の探査技術が発達すれば、埋蔵金の発掘は夢や学問でなく産業になるであろう

　なんと、これまでの発掘を「技術とは言えない」と喝破しているのである。かつて、近所の埋蔵金伝説に、電子ブロックの金属探知器を頼りに闇雲に探そうとしていたワタシなどは、「あぁ、ゴメンナサイ、ゴメンナサイ…」と謝らなくてはならないような勢いなのである。この作者発明者は埋蔵金の探査技術が発達すれば、埋蔵金の発掘は夢や学問でなく産業になるとまで謳いあげるのだった。今さっき、埋蔵金探しは「夢で男のロマンだぁ」と書いたワタシはさらに「ゴメンナサイ、ゴメンナサイ…」と謝らなければならないのである。

　さらに、従来の「埋蔵金探し」を箇条書きに上げ、

• 勘で場所を決めて、縦穴を掘り、さらにいくつもの横穴を掘ったり、ブルトーザーで土を押しのける
• 百年にもわたり、長期間諦めずに掘る

　しかし、そんなミステリー特許に引き込まれていくワタシの心の中のツッコミなど知る由もなく、この埋蔵金小説許では、引き続き具体例を挙げて特許の内容を説明していくことになる。それが、次の「実施例」である。具体的な資料群をもとに、埋蔵金発掘に迫るストーリ〜が書き示されている。

　が、この資料群がスゴイのである。何しろ、こんな感じなのだ。

• 資料A　「常習赤城におよそ三百六十万両。古井戸を掘ることを手がかりとすべし」という水野家に伝わる遺言
• 資料B　「寺の床下から発見された方位図・地図・暗号文書」
• 資料C　「空井戸から発見した銅板と像」
• 資料D　「黄金埋蔵はアッという間にされたらしい、という地元住人のウワサ」

資料Bの一部　「暗号文書」

まさに、歴史ミステリーである

寺の床下から発見された方位図・地図

　しかも、資料Aの「常習赤城におよそ三百六十万両。古井戸を掘ることを手がかりとすべし」という遺言に対しては、「ここで疑問に思うのは、義父が何故もっと詳しく埋蔵場所を教えなかったのか」などと死者にムチ打ち、マジメなのかそれともツッコミ？と言いたくなるような感想・疑問を書き、この疑問に対して延々２ページに渡り超論理的考察、超心理的考察を加えることで、ついには「埋蔵金は七つの古井戸に埋蔵されたことになる」と、超論理科学的に鉄槌結論を下すのである。

 そして、下に示す「寺の床下から発見された方位図・地図・暗号」を基に、黄金分割を始めとする数学的考察などを駆使し、埋蔵金の位置を推定する。しかも、単に推定するだけでなくて、経済的・効率的に発掘をするために埋蔵金の位置の計算誤差を延々と論じて、ついには誤差50cm〜7m弱だと推定するのであった。なるほど、この歴史ミステリー小説特許は単に技術特許にとどまらず、経済を見据えた経済ミステリー特許でもあったのだ。「埋蔵金の発掘は夢や学問でなく産業になる」のだ。

　さて、この埋蔵金ミステリーで指し示された「埋蔵金の埋まっている七つの古井戸」がどこであるかを知りたい人も多いだろう。ということで、特許の図を重ね合わせ、埋蔵金の埋まっている七つの古井戸の場所をプロットしてみたのが、次の図である。どの辺りか判らない人のために、広域地図をリンクしておくとここら辺りということになる。
 

ここが埋蔵金の埋まっている場所だ

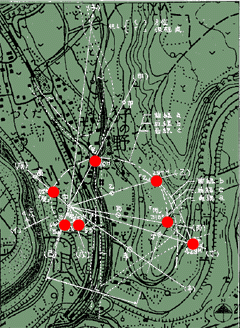　さて、この特許の最後には「なお、この辺りは便利な住宅地向きの環境になりつつあるので、住宅が建設される前に発掘することが望ましい」と
と産業としての指針まで描きつつ筆をおくのである。

　どうだろうか、面白いミステリー小説特許だったのではなかろうか？そして、特許なんて簡単に書ける、と思った人もいるのではないだろうか？そして、どんどん特許を書きたくなる、と思う人も多いに違いない。で、ワタシは思うのだ。できれば、できることであれば、その書いた特許をワタシにも少し分けて頂いて、ワタシのノルマを少しでも減らして欲しい、と強く強く思うのである。
 
 
 

■「やおい」の評価演算子　

ベクトルの彼方で待ってて II

　東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか？

「福田Ｘ小泉っていうのは、結構上手くやっているのかな？」

「あれは、福田Ｘ小泉じゃなくて、絶対あれは小泉Ｘ福田なのー」

「福田Ｘ小泉と小泉Ｘ福田は全然意味が違うのー」

「そう。ただ、ちょっと政治の世界とは違う世界かも〜。政界じゃなくて、やおい界ではー。」

• やおい　→　一部の女性が好む「男性同士の恋愛もののストーリー」のこと
• Ｘ　→　やおいの世界で恋愛の関係を示す記号。例えば、AさんとBさんが恋に落ちるであれば、Aさん×Bさんと表す。で、ここで重要なのは先に位置する方が「攻め役」となって、後に位置する方が「受け役」となる…。つまり、例えばサド侯爵とレオパルド・マゾッホであれば攻め役がサド侯爵で、受け役がマゾッホなので、サド×マゾなのである。決して、マゾ×サドではない…

　で、日本酒を飲みながら、まだまだ続くその話に悪酔いしていると、「カップルの順序が重要なんだー」という言葉を聞いて、ふと中学の頃の数学の授業を思い出した。その頃、大学を出てまだ一年目の斉藤慶子似の数学の先生と話していたときに、「Hくん、あのね掛け合わせる順序が違うと結果も違っちゃう計算もあるのよ」と教わったことがあった。そんな言葉から私は未知の「数学の世界」をかいま見たりしたのである。　今考えてみれば、新任の斉藤慶子似の女性教師の個人授業なのだから、行列・ベクトルの掛け算の順序なんかじゃなくて、「もっと違う順序」を手取り足取り教えてくれても良かったんじゃないか、とか思ったりするし、そうすれば、私は未だ見ぬ「大人の世界」を覗き見ることができたのではないか、と思ったりもするのだけれど、そんなことは残念ながら無くて、私はただ「行列・ベクトルの世界」を覗いただけだったのである。

　で、そんな昔話を思い出したせいか、頭の中でこんな風に思ったのである。そういえば、これまで「できるかな?」では数多く「恋の力学」でも遊んできた。ただ、そこでは「惹かれ合う恋心の大きさ」だけに注目して、そのカップルの中での役割などは考えたことがなかった。そこで、今回は「やおい」のカップルの「役割・順序」に注目し、その「役割・順序」を評価する演算子を行列・ベクトルの掛け算になぞらえながら考えてみることで、これまでと同じく色々な「恋の形」を眺めてみたいと思う。
 

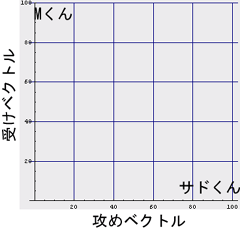
　まずは、色々な人物（実際の人物であったり、小説などの登場人物であったり）のタイプを二次元空間に配置しよう。「この人は結構攻め役が合いそう」とか「この人は絶対受け役が合うのだー」という適性を

1. 攻めベクトル
2. 受けベクトル

SM平面上のサドくんとMくん

　そして、カップリング適性では「A×B、B×Aが全然違う」ということから、外積(ベクトル積)をそのまま流用して、適当な評価関数を作ってみるのが自然だろう。まず、

カップリング適性ベクトル = （攻め度(s)、受け度(m)）

A×Bのカップリング適性 = ( As * Bm - Am * Bs )
　　　　　　　　　　　　　　　 = Aさんの攻め度 * Bさんの受け度
　　　　　　　　　　　　　　　　　　- Aさんの受け度 * Bさんの攻め度

　とりあえず、今回はこの評価演算子を作成するところまでで終えたいと思うが、いずれこの「やおいの評価演算子」を武器にして、いつか（?）「やおいの世界= やおい界」に限らず、色んな数多くの恋の関係を目に見えるようにしてみたいと思う。そして、これまで数多く考えてきた「恋の〜シリーズ」を充実させていきたいと思うのである。

　ところで、今回のカップリング適性評価演算子は基本的に外積そのものである。つまり、この演算が返す値は「二人のベクトルでできる平行四辺形の面積」に等しい。つまりは、「二人のベクトルでどれだけ色んな違うことがきでるか」を示す尺度である。そして、その値は二人のベクトルが直交する時、すなわち二人のベクトルが重ならず独立である時に最大値となる。つまりは、「二人のベクトルが違えば違うほど大きく」なる。例えば、先の「サドくん×Mくん」であれば二人のS,M趣向が完全に正反対であったからとてもお似合いのカップルになったのである。

　これをいわゆる恋の話で考えてみると、とっても独立な二人、趣味が重ならない二人がお似合いだということになる。なるほど、そんなカップルも世の中にはたくさんいることだろう。そんな人達を「外積タイプのカップル」と呼ぶことができると思う。

　一方、趣味が重ならないカップルだけでなくて、世の中にはそれとは正反対の「趣味が重なる良いカップル」も数多くいる。それは「内積タイプのカップル」である。内積はA,Bベクトル間の正射影に比例する量であって、つまりは「二人の重なるベクトルの大きさ」である。それは例えば、相手の中に自分を重ね合わせるような「二人の重なる部分が二人を結びつけるようなカップル」なのである。

　「理系と文系」・「男と女」が対極的なものでも、相反するものでもないのと同じく、「外積カップルと内積カップル」も別に二つに分けられるようなものではないだろう。「外積タイプの恋」も「内積タイプの恋」が混じり合って、それぞれに良いところもあれば、危ういところもあって、などと想像してみるのも面白いに違いない。そして、さらにはもしかしたらベクトル空間で萌えることができるようになったりするかもしれない。
 

　そういえば、ふと考えてみると以前「恋の形を見た人は」で最後に引用した本橋馨子の「兼次おじ様シリーズ」は男性同士の恋の話だった。つまりは「やおい」の話だった。そこで、もう一度そのセリフを最後に飾って眺めてみようと思うのである。
 

「愛はどんな形をしているか知っているか？」

「見た事ないからわかりません。」

「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...
もし愛に優劣を決めるものがあればなんだろう？... 異性愛か、同性愛か、そんなものじゃない　　…たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」