1999-02-26[n年前へ]
■ヒトは電磁波の振動方向を見ることができるか? 
はい。ハイディンガーのブラシをご覧下さい
(1999.02.26)
リチャード・ファインマンの本の中で次のような問題があったように思う。
「偏光板がフィルターが一枚だけある。その偏光フィルターの偏光方向をどのようにして知れば良いか?」
その本の中での答えは、
「物体の反射光を偏光フィルターを通して見てみる。」
だった。ブルースター角で入射した光の反射光は、入射面に対して電場の振動方向が垂直になっている、ということを利用するわけである。
分かりやすいように、偏光フィルターを通してみたガラスの反射光をデジカメで撮影してみる。左が反射光を通すような角度に偏光フィルターを回したものであり、右が反射光をカットするような角度に偏光フィルターを回した場合である。この左の場合、すなわち、反射光が一番通過している角度から液晶の偏光面がわかるわけである。
 |  |
ところで、このようなファインマンが示したような方法を用いなくても、そもそもヒトは電磁波の振動方向を見ることができるのである。以前、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「鳥は太陽の位置、光の偏光パターンを位置のセンサーに使う」という話があった。ヒトも同じく光の偏光方向、すなわち、電磁波の振動方向を見ることができるのである。鳥はどう見えるかは私にはわからないが、ヒトならば自らが実験台になれるので、電磁波振動方向をどう見ることができるか調べてみたい。というわけで、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「近日中にある実験をする予定である」と書いたものが今回の確認実験である。なお、光の進行方向と磁界の振動方向を含む面を「偏光面」、電界の振動面を含む面を「振動面」と呼ぶ。
電磁波の振動方向をヒトが見ると「ハイディンガーのブラシ "Haidinger'sBrushes"」というものが見える。それを知ったのは、いつものごとく「物理の散歩道」からである。網膜に複屈折性があるために「ハイディンガーのブラシ」が見えるのだという。
私はこれまで、「ハイディンガーのブラシ "Haidinger's Brushes"」を見たことがない。いや、正確に言えば意識したことがない。そこで、判別しやすいように直線偏光を用意してやることにした。そこで、東急ハンズで偏光フィルターを買ってきた。
そして、空を見てみる。もちろん、偏光の偏りが強い、太陽を中心にして90度の角度をなす同心円方向である。詳しくは、
- 可視-赤外域での偏光観測による衛星観測手法の開発基礎研究(http://www.mri-jma.go.jp/Dep/sa/Lab1/labt01-s.html)
- エアロゾル観測(http://mars.im.kindai.ac.jp/KISYO/YPROJECT/kansoku.html)
さて、ヒトである私は、空を眺めて格闘すること5分程で、「ハイディンガーのブラシ"Haidinger's Brushes"」がわかるようになった。私が見たハイディンガーのブラシ"Haidinger's Brushes"を示す。
 |
この絵で太陽の方向は右上であり、偏光面は次の絵の青の矢印方向になる。
 |
というわけで、ヒト(少なくとも私は)電磁波の振動方向を見ることができるのである。慣れてしまうと、白い紙を見つめているときなども(条件によっては)見えるようになる。色を扱う人は意識すると面白いと思う。
ところで、偏光フィルターがどういうものか知らない人のために、NotePCの液晶に偏光フィルターを重ねた写真を示す。
 |  |
なぜ、こうなるかわからない方は、
などを参考にして欲しい。液晶ディスプレイの構造がわかると思う。そして、面白いことに気づいた。NotePCの液晶からの光は直線偏光である。ということは、NotePCの液晶にはハイディンガーのブラシが映っているのである。正確に言えば、NotePCの液晶を見ているあなたの視界の中央には、ハイディンガーのブラシが映っているのである。と、気づいてみると確かに見えている。
というわけで、液晶ディスプレイを使用している方はハイディンガーのブラシを見て頂きたい。以下のやり方がわかりやすいと思う。
1.このWindowを最大化する
2.下へスクロールして画面を真っ白にする。
3.液晶ディスプレイ(NotePC)を回転させる。
4.画面(視点)の中央に(視点に対して位置が)動かない黄色いもやが見えるはず。もちろん、回転はする。
液晶ディスプレイやヘッドマウントディスプレイ(HMD)を色々見てみたが、どれにもハイディンガーのブラシは存在していた。視界の中央に不思議な十字架のように現れているのである。現代の液晶技術が負う十字架である。
誰もが、目の前にあるのにそれに気づかないというのも、実に面白い。まるで、「青い鳥」のようである。そして、そういうことはとても多いのではないかと思う。それはそれで面白い話だ。
- それでは、ハイディンガーのブラシをご覧下さい -
1999-03-25[n年前へ]
■電界計算をしてみたい[有限要素法編その1] 
有限と微小のパン
今回のサブタイトルは一目瞭然であるが、森博嗣のミステリのタイトルそのままである。
 |
何故、「電界計算をしてみたい-有限要素法編その1-」が「有限と微小のパン」に繋がるのか。もちろん、"有限要素法"と"有限と微小のパン"の「有限」をかけた駄洒落ではない。有限要素法を考えるとき、私は森博嗣に足を向けては寝ることができない。それが、なぜかは下の本を見ればわかる。
 |
これは、学生時代に有限要素法を勉強するために使った本である。「森 博嗣 著」と書いてあるのがわかるだろうか。いや、まさかこの本の作者がミステリを量産するとは想像もしなかった。ビックリである。講談社ノベルズと森北出版の両方から本を出している人は他にはいそうにない。
本題と関係のない話はここまでにしておく。今回はMathematicaで有限要素法を用いて静電界計算を行いたい。とりあえず、ソルバーとプリ・プロセッサまでつくる。その応用は続きの回で行いたい。Mathematicaで有限要素法を勉強するには、森北出版の依田 潔 著「Mathematicaによる電磁界シミュレーション入門」を参考にした。任意の電荷配置のPoisson方程式を解くようにしてある。
次回に詳しく計算モデルの説明を行うので、今回は計算モデルの詳細については記述しない。Notebook内に、モデルの詳細は記述してある。
このNotebookを使った計算、出力例を以下に示す。
| 平行平板電極の間に誘電体層があるモデル | 平板電極と三角柱電極の間に誘電体層があるモデル | 平板電極と円柱電極の間に誘電体層があるモデル |
 分割要素 |  分割要素 |  分割要素 |
 電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |
 半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |
Mathematica3.0のHTML出力は大変便利だが、漢字が化けるのが困りものだ。しかも、ちょっと似た漢字に化けてしまうからわかりにくい。今回のNotebook中で化けた漢字を以下に示す。
- 油界 <- 電界
- 堰素 <- 要素
- 誘油 <- 誘電
- 姦み込む <- 組み込む
- 表傭 <- 表面
- 壓さ <- 高さ
- 堆心 <- 重心
- 肖似 <- 近似
- 内占 <- 内部
- 傭積 <- 面積
- 回寂 <- 回転
- 進当 <- 適当
- 懷瞰 <- 鳥瞰
中国語みたいな化け方である。しかも、意味としても何か変な化け方である。いつか、この対処方法と理由を考えてみたい。それにしても、週末の遊び道具としてはMathematicaは素晴らしいと思う。
2000-01-27[n年前へ]
■「富士の樹海」を目指せ 
磁界を可視化しよう
以前から探していた「面白いもの」を入手した。この写真がその「面白いもの」なのであるが、何だかわかるだろうか? ちなみに、大きさは「1cm×5cm」位のシートである。
 |
これは「マグネビュアー」というものである。磁界を可視化してくれるシートだ。マイラーフィルムの間に磁性体を混入させたマイクロカプセルを入れることで、磁界に対する配向性を持たせたものだ。と、言葉でいってもなかなかわかりにくいので、磁界を可視化した写真を示してみる。何しろ、百聞は一見に如かずである。
次の写真は某ピザ店のマグネットシート(よく冷蔵庫の扉に張り付ける奴)の上に「マグネビュアー」をのせたところである。ピザ屋は私の食生活を支えていると言っても良い。私が生きているのはピザ屋のおかげである。
 |
私の「命の恩人」でもある某ピザ店のマグネットシートがつくる磁界が見て取れるだろう。磁界が可視化されているのである。
本WEBではこれまで様々な「可視化」で遊んできた。例えば、
- 感温液晶でNotePCの発熱分布を可視化する
- ハードディスクのエントロピーは増大するか?- デフラグと突然変異の共通点 - (1999.03.28)
- 夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
- 恋の力学 -恋の無限摂動 - (1999.12.21)
- WEBサイトの絆 - WEBの世界を可視化しよう- (2000.01.13)
- 夜のバットマン - 超音波を可視化しよう- (2000.01.17)
上に示した「某ピザ店のマグネットシートの表面」の磁界の様子も面白いが、もっと面白いのは「某ピザ店のマグネットシートの境界」の磁界を可視化したものである。
それが下の写真である。磁界の様子が実感できるのではないだろうか?
 |
下に示す図はドーナツ型の磁石の周りの磁界をCUPSを用いてシミュレーション計算した結果である。この計算結果と同じようなものが「マグネビュアー」を使うと簡単に可視化できる。
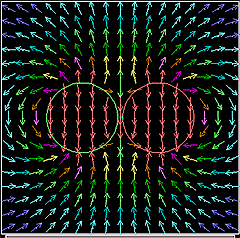 |
普通、こういった磁界の可視化は磁気造影剤や砂鉄みたいな磁性体粒子を用いるのであるが、そういったものはどうにもハンドリング性にかける。液体や粉体などを家の中で実験に使うのはイヤである。いや、もちろん仕事で使うのもイヤであるが... そこで、この「マグネビュアー」が登場するわけだ。
それでは、その他の面白そうな磁界を可視化してみたい。磁界と言えば、やはりアレの登場だろう。もちろん、アレと言えば磁気カードである。クレジットカードや銀行のキャッシュカードといった磁気カードだ。一例を次に示してみる。こんなヤツだ。
 |
カードの下に黒い磁気データ記録部があるのがわかるだろう。
それでは、その「磁気データ記録部」に「マグネビュアー」をのせてみよう。はたして、磁気データは可視化されるだろうか?
 |
といっても、この写真ではわかりにくいので、「マグネビュアー」を拡大してみよう。すると、バーコードのような模様が見えるのがわかると思う。「磁気データ」が簡単に可視化されているわけである。この「マグネビュアー」と普通のスキャナーがあれば磁気データ読み取り機がなくても磁気データが読みとれるのである。
 |
しかし、このカードに関しては内容を解析するとマズイ事情があるので、次回に「ソフマップ」のカードを題材にして磁気カードの内容を可視化してみるつもりだ。題して、
- ソフマップでお買い物 - 磁界の可視化とバーコード - (仮称)
さて、話は変わるが、私はこの「マグネビュアー」を手に「富士の樹海」を目指すつもりだ。「富士の樹海」では」方位磁針が変な方向を示すと伝えられている。そしてまた「富士の麓」ではとかく人は判断を誤りやすいとも聞く。船頭多くして船山に登ると言うが、「富士の樹海」には判断を誤った船が沈没しまくりである。
私は「富士の樹海」の真実をこの「マグネビュアー」で明らかにするつもりだ。「富士の樹海」の謎を明らかにするのである。何故、方位がそして人が判断を誤るのか、その謎を明らかにするのだ。
しかし、もしも、もしも、の話であるが、本WEBの更新が止まった際には、「富士の樹海」で私が眠っていると思って欲しい。「マグネビュアー」が役に立たないはずがないのだが、きっと何か判断を間違えたのであろう。そうそう、あくまで「富士の樹海」である。「富士の裾野」ではないので念のため...
2000-01-30[n年前へ]
■ソフマップでお買い物 
磁界の可視化とバーコード
前回、
で「マグネビュアー」を使って磁界の可視化をして遊んでみた。今回はその続きである。ソフマップの磁気カードの中に書き込まれている磁気データを可視化して調べてみるのである。磁気カードには、
- 銀行のキャッシュカード
- クレジットカード
- テレホンカード
- オレンジカード
まずは、ソフマップカードの写真を示してみよう。これがソフマップで買い物をするたびにお世話になるソフマップカードである。
 |
この写真からではどこにデータが書き込まれているのかわからない。そこで、「マグネビュアー」の登場と言いたいところであるが、残念ながら今回は「マグネビュアー」は登場しないのである。「マグネビュアー」はとても便利なのであるが、さすがに磁気カードの磁気データを読もうとすると分解能が不足する恐れがある。
そこで、代打選手に登場願うことにした。代打選手はキヤノン製のLBPのトナーである。以前、
の時に「トナーはクーロン力で制御されて画像を作るのだ」という話があった。キヤノン製の白黒のLBPではクーロン力に加えて磁気力を使ってトナーを制御している。なので、キヤノン製の白黒トナーは磁性体粉末ということになる。テレホンカードが出た頃はキヤノン製のトナーを使ってデータを読み出していた人も多いはずである。みな、テレホンカードの表面を削りトナーを振り掛けていたのである。というのは、聞いた話であり、実体験に基づくものでは絶対にない。神に誓っても良い。その頃にキヤノン製のトナーを使い倒していたということは絶対にないのである。しかも、その数年後に(以下略)。
それでは、磁性体の微少粉末であるトナーをソフマップカードに振り掛けてみよう。
 |
ソフマップカードの磁気データが可視化されたのがわかると思う。磁気によるバーコードが見えるだろう。これがソフマップカードに書き込まれている磁気データである。
とはいえ、トナーの付着具合にムラがある。それは私が雑に実験を行ったからである。こんなにムラがあっても磁気コードが判別できるかどうか疑問を持たれる方も多いと思う。しかし、
- 読む方向に対して垂直な線が多い
- 読む方向に対して水平な線は少ない
そのようにして、ノイズを減らし、S/N比を上げた画像を示してみる。
どうだろうか、驚くほど綺麗になっているのがわかると思う。まさか、と思われるかもしれないが本当である。
さて、これはソフマップカードの磁気データの全体像であるが、もう少し拡大したものを以下に示す。
 |
極めて明瞭に磁気データが可視化されているのがわかると思う。これはトナーを振りかけて、1万円ちょっとのスキャナ(CanonのUSB接続の安物スキャナ)で読み込んだものに対して先の処理をしただけである。これほど明瞭になるのも、全て1次元バーコードの特徴のおかげである。磁気ヘッドの制作などをしなくても良いのである。
磁気カードの記録密度は銀行統一仕様(NTT)でもISO3554でも8.3bit/mm=211bit/inchであるから、最近の600dpi(dot/inch)程度のスキャナーであれば十分磁気データの画像読みとりが可能である。
それでは、もっと拡大してみる。拡大する部分は上の画像の右の辺りである。すると、このようになる。
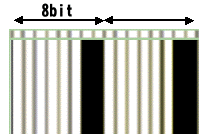 |
データ間隔がわかりやすいように、ここでは矢印や文字を書き入れている。この画像を見ると、磁気データは規則的な細かい周期性を持ち、その周期でいうと8つ単位でさらなる周期性があるように思われる。つまり、8bitをひとまとまりとしたデータが書き込まれているように見える。例えば、上の画像では
- ( 白、白、白、白、白、白、黒、黒 ) x 2
- ( 00000011 ) x 2
- ( ああああああたた ) x 2
複数枚のカードのこの部分を比較してみれば、比較的容易にデータ構造は解析することができるだろう。また、一枚のカードからでもカード番号などの数字と磁気データを比較することにより、解析することはやはり困難無しに解析できると思うのである。と、思うわけではあるが、あまりやりすぎるのはマズイと思われるので、今回はこれまでにしておく。
2007-12-31[n年前へ]
■サントリーDAKARAを近づけるとクルクル回るブタさん人形のヒミツ 
少し前、サントリーのスポーツ飲料DAKARAのオマケにブタさん人形が付いていた。ピグリンという名前が付いているらしいそのブタさん人形には、小さなDAKARAボトルも付属していて、ブタさん人形にDAKARAボトルを近づけるとブタさんがグルグル回りだすのだった。これが、本当に驚くほど早く回転し続けて、実に楽しくなるのである。
クルクル回って気持ち良くなるのはさておき、その動作の仕組みが気になってしまうのが人情でもある。ブタさん人形とボトルには磁石が入っていることはすぐにわかるのだけれども、単に磁石が(何の工夫もなく)入っているだけでは、DAKARAボトルと人形が近づいたり遠ざかったりすることはあっても、素直にクルクルと回るとは思えない。
かといって、人形やボトルを分解したら、その仕掛けも簡単にわかりそうだが、分解するにはブタさん人形はあまりに可愛いすぎる…。そこで、ブタさん人形に手元にあった磁石を近づけたり、そのときの反応を観察したりしているうちに、その仕掛けが大体わかってきた。おそらく、「ボトルの中には傾けられた磁石が入っていて」「ぶたさん人形の底面が球面状になっている」という2点の工夫により、DAKARAボトルを近づけるとピグリンがクルクル回りだす、のである。

 ブタさん人形とDAKARAボトルを向きを逆にしてくっつけてみると、DAKARAボトルの向きによってくっつき方が異なるのがわかる。そうなる理由は、DAKARAボトルの中の磁石が傾いて配置されている、と考えるのが一番素直である。たとえば、ブタさん人形の中にはN極を下に向け、S極を上に向けた磁石が水平に取り付けてあり、DAKARAボトルの中には、N極を下(から少しずらした方向)に向け、S極を上(から少しずらした方向)に向けた磁石が取り付けてあるというわけだ。DAKARAボトルの中の磁石を、水平面に対し角度を持たせて固定しておくのである。
ブタさん人形とDAKARAボトルを向きを逆にしてくっつけてみると、DAKARAボトルの向きによってくっつき方が異なるのがわかる。そうなる理由は、DAKARAボトルの中の磁石が傾いて配置されている、と考えるのが一番素直である。たとえば、ブタさん人形の中にはN極を下に向け、S極を上に向けた磁石が水平に取り付けてあり、DAKARAボトルの中には、N極を下(から少しずらした方向)に向け、S極を上(から少しずらした方向)に向けた磁石が取り付けてあるというわけだ。DAKARAボトルの中の磁石を、水平面に対し角度を持たせて固定しておくのである。
すると、上に書いた図のように、DAKARAボトルを近づけると、互いの磁石の反発力でブタさん人形は(ブタさん人形の向きによらず)鉛直面に対して(DAKARAボトルに対して)特定方向に傾くことになる。そして、その傾いた状態で(これまた磁石の反発力で)DAKARAボトルから遠ざかろうとする。すると、その結果、ぶたさん人形の底面が球面状になっているので、傾いたコマのようにクルクル回りながらDAKARAボトルから離れていく、という動きをするわけである。
「するわけである」と書いたが、もちろん人形の中身を調べたわけではないので、実際のところどうなのかはわからない。とはいえ、やはりブタさん人形は妙に可愛いので、分解する気にはなれない。というわけで、仕組みを納得できる考えが生まれたところで終わりにしておこう。



