1999-06-28[n年前へ]
■風呂場の水滴を考える。 
オールヌードの研究員
風呂場の天井から浴槽めがけて、水滴がしたたって音がしているのはよくある風景である。ピーンという(もちろん人によっても印象は違うのだろうが)気持ちのいい音がしている。似たようなものとしては、水琴窟などもある。この音がなぜ鳴るかは、ロゲルギストの「物理の散歩道」に詳しい考察がある。それによれば、水滴が一粒落ちたように見えても、実は何粒かに別れており、ちょうどカルガモの親子のようになっているという。つまり、大きな親の水滴の一粒の後を、何粒かの小さな子どもの水滴が追いかけているという具合である。まず、水滴の親が水面に空洞をつくり、その中に子どもの水滴が飛び込むことにより音が出るという。結局、水滴の音を作っているのは、その子どもの水滴の方だという。「物理の散歩道」の中では、針をつたって水滴を落とせば、子どもの水滴ができないという。
風呂に入って、濡らした手から水滴を落としてみる。指の爪の先から水滴を落とすと音はほとんどしないが、指の「はら」から落とすと派手に音がする。ぜひ、自分でも確かめていただきたい。
爪先は比較的尖っているので、落ちる水滴は一粒だが、比較的平らな指の「はら」からの場合には、カルガモ親子のような水滴が落ちているせいだろう。
なぜ、このような違いが生じるかを推測してみたい。まずは、下の絵を見て欲しい。
 |  |
上の上手な絵が言いたいのは、次のような推測である。
- 平らな表面から水滴が落ちる際には、長く伸びた水のブリッジが出来ていて、1つぶ目の水滴が落ちた後も、このブリッジ部分が「カルガモの子ども」のように小さな水滴となって後を追いかけていくのではないか。
- それに対して、尖った表面から水滴が落ちる際には、先のブリッジ部分のほとんどは水でないため、後続の水滴は発生しない。
計算モデルとしてどのようなものを使うかであるが、私の知っている範囲では大きく分けて2種類のやり方がある。
- 流体をモデル計算する。すなわち、Navier-Stokesの方程式を解く。
- 流体を粒子のようなものの連続体として解く(ex.格子ボルツマン法)
電気通信大学情報工学科情報数理工学講座渡辺研究室( http://assam.im.uec.ac.jp/fluid.html )
 |
また、水滴が水面に衝突する状態の計算は、電気通信大学情報工学科情報数理工学講座渡辺研究室にもあるし、他にもNaSt2DというFreeの2次元Navier-Stokes方程式のソルバーを用いて行われた計算結果が
http://www5.informatik.tu-muenchen.de/forschung/visualisierung/praktikum.html
にある。
 |
Michael Griebel氏らによるNast2Dのコードは公開されているので、その中身をいじりながら、計算を行う予定である。
とりあえず、今回はバックグラウンドを紹介する所までで、次回(といってもすぐではないだろう)に計算の本番に入りたい。
手のひらの実験から考えると、風呂場で水滴の音が聞こえるのは天井が平らなせいだということになる。ならば、鍾乳石のようなつらら形状の天井の風呂場では音がしないのだろうか?しかし、水滴は空気中で落下していく最中には空気の抵抗をうける。そのため、大きな水滴は落ちる最中に分裂し、複数の水滴になってしまう。
となると、
- 落ちる水滴の最初の大きさは、どう決まっているのか。
- 水滴は落下するスピード、水滴の大きさがどの程度になると分裂するのか?
ところで、インクジェット方式のカラープリンターも液滴で画像を描くのだから、液滴の様子は重要な筈である。液滴が飛び散ってしまっては困るし、位置がずれても困る。各社ともカルガモの子ども水滴をなくすために色々工夫をこらしている筈だ。
実は風呂場の水滴問題は重要で、奥が深いのだ。オールヌードで私は考えるのであった。
1999-07-25[n年前へ]
■君はトナーを見たか? 
6umの高速飛行物体
今回の話はミステリー小説のように、「嘘を意識して書きはしないが、本当のことも意識的に書かない」部分がある。お読みの際は注意が必要である。
先日、大手町で開催されていた「JapanHardCopy'99」を見ていた。ちなみに「JapanHardCopy」というのは電子写真装置(複写機やレーザービームプリンター)やインクジェットプリンターなど画像を印字する機械に関する学会である「日本画像学会」が主催するシンポジウムである。その中でも、一番よく「覚えている」発表を考察を含めながら紹介したいと思う。とても「できるかな?」と共通の匂いがするのだ? それに15分の発表がまるまるビデオ(を液晶プロジェクターに表示したもの)によるものというのも珍しいと思う(画面上に時々タイミングを知らせるマーキングが出てはいたが、発表者は喋る長さ調整に苦労していたと思う)。
それは、
現像プロセスにおけるトナー粒子の挙動測定
という発表だ。
この発表は電子写真式の装置の現像装置でトナーが現像される様子を計測した結果の報告である。以前、
ゼロックス写真とセンチメンタルな写真 -コピー機による画像表現について考える - (99.06.06)
の時に電子写真プロセスについて紹介した。今回もその簡単な構成を示しておく。このような機構がコピー機やLBPの内部には入っているのだ。(ドラム表面の画としてはRicohのWEBがわかりやすい。)
 |
上の概略図で現像装置は右の薄紫の円である。感光ドラムが中央の大きな円だ。この発表は、現像装置と感光ドラムの近接部(画面中央のの赤丸で囲まれた部分)で何が起きているかを測定しているのだ。
しかし、全ての現像装置ではなく現像装置と感光ドラムが非接触のタイプのものに関する報告である。現像装置から感光ドラムへトナーを現像させてやるわけだが、両者が非接触であるということはトナー粒子を現像装置から飛ばしてやることにより現像させるわけである。高電界を印加して電気的な力によりトナー粒子を飛翔させるのだ。そのような場合にトナー粒子がどのような挙動を示しているかを計測しているのである。
現像装置と感光ドラムの間の距離というのは通常300um程度である。また、最近のトナーの粒径は6um程度である。300umのギャップ中を6um程度の飛行物体が数多く飛びまくるのである。数多くといってもピンとこないかもしれないので、数値的な考察をしてみる。1cm^2(1平方センチメートル)の黒い四角を印刷するのにトナー粒子はどのていど必要だろうか。もしトナー1個が10um角の領域を完全に覆えるならトナーが1000x1000個あれば1cm^2の区画を完全に覆えるだろう。しかし、現実問題として1層だけでは覆えるわけがないので仮に5層必要だとすると、5x10^6個のトナーが1cm^2(1平方センチメートル)の黒い四角を印刷するのに使われていることになる。500万個である。
その数多いトナー粒子が飛行しているものの中から1個単位のトナー粒子を計測しどのような飛行をしているかを調べているのだ。数100um角の領域中で数百万個のトナーが飛行する中から1個のトナー粒子を調べるのである。まるで、大都会で一人の人の追跡取材し、その人にライトをあてるような作業ではないか。ロマンチックとは思えないだろうか?
それでは、どのように飛行しているかを予稿集の図から抜き出してみよう。
 |
この写真中では画面上のドラムと現像装置は500um離れている。また、上と下の写真ではトナーを飛行させるための電界の波形が異なる。上が単純な矩形波であり、下が矩形波の正と負の電界がかかる時間長さが異なるものである。まるでトナー粒子の動きが物理的なオシロスコープのようである。
これはほぼ1/15秒間の軌跡であり、予稿集の写真から推定するに、その間に7cm程度は移動している。ということはトナー粒子は1秒間に1m程度は移動していることになる。秒速1mである。しかも方向を鋭く変えながらであるから、加速度としては凄いものがあるし、瞬間の最大速度もはるかにこれより速いだろう。
普段LBPなどで出力をすることも多いと思うが、その出力画像を形成しているトナー粒子たちがこんなに高速でアクロバット飛行してきたとは知らなかった人も多いだろう。この写真自体は今回の発表の導入部分に過ぎなく、本題がこの後に続くのだが、結構面白い写真ではないだろうか。トナー粒子の動きが一目瞭然である。
ところで、ここまできても「おまえの考察が少なすぎるぞ。」と言われる方はいらっしゃらないですよね。「これ、おまえの発表じゃないか。自作自演じゃないか。」とおっしゃる方はいるでしょうけど。
1999-09-01[n年前へ]
■画像に関する場の理論 
ポイントは画像形成の物理性だ!?
今回は、
夏目漱石は温泉がお好き? - 文章構造を可視化するソフトをつくる- (1999.07.14)
の回と同じく、「可視化情報シンポジウム'99」から話は始まる。まずは、「可視化情報シンポジウム'99」の中の
ウェーブレット変換法と微積分方程式によるカラー画像の圧縮および再現性について
という予稿の冒頭部分を抜き出してみる。「コンピュータグラフィックスを構成する画素データをスカラーポテンシャルあるいはベクトルポテンシャルの1成分とみなし、ベクトルの概念を導入することで古典物理学の集大成である場の理論が適用可能であることを提案している」というフレーズがある。
着目点は面白いし、この文章自体もファンタジーで私のツボに近い。しかしながら、肝心の内容が私の趣向とは少し違った。何しろ「以上により本研究では、古典物理学の場の理論で用いられるラプラシアン演算を用いることで、画像のエッジ抽出が行えることがわかった。」というようなフレーズが出てくるのである。うーん。
私と同様の印象を受けた人も他にいたようで(当然いると思うが)、「エッジ強調・抽出のために画像のラプラシアンをとるのはごく普通に行われていることだと思うのですが、何か新しい事項などあるのでしょうか?」という質問をしていた人もいた。
また、話の後半では、画像圧縮のために、ラプラシアンをかけたデータに積分方程式や有限要素法などを用いて解くことにより、画像圧縮復元をしようと試みていたが、これも精度、圧縮率、計算コストを考えるといま一つであると思う(私としては)。
画像とポテンシャルを結びつけて考えることは多い。例えば、「できるかな?」の中からでも抜き出してみると、
- 分数階微分に基づく画像特性を考えてみたい- 同じ年齢でも大違い - (1999.02.28)
- ゼロックス写真とセンチメンタルな写真 - コピー機による画像表現について考える- (99.06.06)
- コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
現実問題として、実世界において画像形成をを行うには物理学的な現象を介して行う以外にはありえない。「いや、そんなことはない。心理学的に、誰かがオレの脳みそに画像を飛ばしてくる。」というブラックなことを仰る方もいるだろうが、それはちょっと別にしておきたい。
「できるかな?」に登場している画像を形成装置には、
コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
で扱ったコピー機などの電子写真装置や、
宇宙人はどこにいる? - 画像復元を勉強してみたいその1-(1999.01.10)
で扱ったカメラ。望遠鏡などの光学系や、
ヒトは電磁波の振動方向を見ることができるか?- はい。ハイディンガーのブラシをご覧下さい - (1999.02.26)
で扱った液晶ディスプレイなどがある。そのいずれもが、純物理学的な現象を用いた画像形成の装置である。
例えば、プラズマディスプレイなどはプラズマアドレス部分に放電を生じさせて、電荷を液晶背面に付着させて、その電荷により発生する電界によって液晶の配向方向を変化させて、透過率を変化させることにより、画像を形成するのである。
 |
また、逆問題のようであるが電界・電荷分布測定などを目的として液晶のボッケルス効果を用いることも多い。液晶を用いて得られる画像から、電界分布や電荷分布を計測するわけである。これなども画像と場の理論が直に結びついている一例である。
参考に、SHARPのプラズマアドレスディスプレイを示しておく。
 |
また、電子写真装置などは感光体表面に電荷分布を形成し、その電位像をトナーという電荷粒子で可視化するのであるから、電磁場を用いて画像形成をしているわけである。だから、場の理論を持ちこむのは至極当然であり、有用性も非常に高いだろう。そういった視点で考察してみたのが、
である。 同様に、画像圧縮に関しても、画像形成の物理性に着目することで実現できる場合も多いと思うのであるが、それは次回にしておく。
2000-01-27[n年前へ]
■「富士の樹海」を目指せ 
磁界を可視化しよう
以前から探していた「面白いもの」を入手した。この写真がその「面白いもの」なのであるが、何だかわかるだろうか? ちなみに、大きさは「1cm×5cm」位のシートである。
 |
これは「マグネビュアー」というものである。磁界を可視化してくれるシートだ。マイラーフィルムの間に磁性体を混入させたマイクロカプセルを入れることで、磁界に対する配向性を持たせたものだ。と、言葉でいってもなかなかわかりにくいので、磁界を可視化した写真を示してみる。何しろ、百聞は一見に如かずである。
次の写真は某ピザ店のマグネットシート(よく冷蔵庫の扉に張り付ける奴)の上に「マグネビュアー」をのせたところである。ピザ屋は私の食生活を支えていると言っても良い。私が生きているのはピザ屋のおかげである。
 |
私の「命の恩人」でもある某ピザ店のマグネットシートがつくる磁界が見て取れるだろう。磁界が可視化されているのである。
本WEBではこれまで様々な「可視化」で遊んできた。例えば、
- 感温液晶でNotePCの発熱分布を可視化する
- ハードディスクのエントロピーは増大するか?- デフラグと突然変異の共通点 - (1999.03.28)
- 夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
- 恋の力学 -恋の無限摂動 - (1999.12.21)
- WEBサイトの絆 - WEBの世界を可視化しよう- (2000.01.13)
- 夜のバットマン - 超音波を可視化しよう- (2000.01.17)
上に示した「某ピザ店のマグネットシートの表面」の磁界の様子も面白いが、もっと面白いのは「某ピザ店のマグネットシートの境界」の磁界を可視化したものである。
それが下の写真である。磁界の様子が実感できるのではないだろうか?
 |
下に示す図はドーナツ型の磁石の周りの磁界をCUPSを用いてシミュレーション計算した結果である。この計算結果と同じようなものが「マグネビュアー」を使うと簡単に可視化できる。
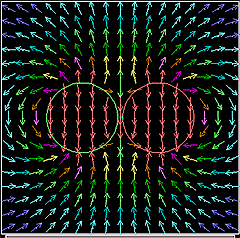 |
普通、こういった磁界の可視化は磁気造影剤や砂鉄みたいな磁性体粒子を用いるのであるが、そういったものはどうにもハンドリング性にかける。液体や粉体などを家の中で実験に使うのはイヤである。いや、もちろん仕事で使うのもイヤであるが... そこで、この「マグネビュアー」が登場するわけだ。
それでは、その他の面白そうな磁界を可視化してみたい。磁界と言えば、やはりアレの登場だろう。もちろん、アレと言えば磁気カードである。クレジットカードや銀行のキャッシュカードといった磁気カードだ。一例を次に示してみる。こんなヤツだ。
 |
カードの下に黒い磁気データ記録部があるのがわかるだろう。
それでは、その「磁気データ記録部」に「マグネビュアー」をのせてみよう。はたして、磁気データは可視化されるだろうか?
 |
といっても、この写真ではわかりにくいので、「マグネビュアー」を拡大してみよう。すると、バーコードのような模様が見えるのがわかると思う。「磁気データ」が簡単に可視化されているわけである。この「マグネビュアー」と普通のスキャナーがあれば磁気データ読み取り機がなくても磁気データが読みとれるのである。
 |
しかし、このカードに関しては内容を解析するとマズイ事情があるので、次回に「ソフマップ」のカードを題材にして磁気カードの内容を可視化してみるつもりだ。題して、
- ソフマップでお買い物 - 磁界の可視化とバーコード - (仮称)
さて、話は変わるが、私はこの「マグネビュアー」を手に「富士の樹海」を目指すつもりだ。「富士の樹海」では」方位磁針が変な方向を示すと伝えられている。そしてまた「富士の麓」ではとかく人は判断を誤りやすいとも聞く。船頭多くして船山に登ると言うが、「富士の樹海」には判断を誤った船が沈没しまくりである。
私は「富士の樹海」の真実をこの「マグネビュアー」で明らかにするつもりだ。「富士の樹海」の謎を明らかにするのである。何故、方位がそして人が判断を誤るのか、その謎を明らかにするのだ。
しかし、もしも、もしも、の話であるが、本WEBの更新が止まった際には、「富士の樹海」で私が眠っていると思って欲しい。「マグネビュアー」が役に立たないはずがないのだが、きっと何か判断を間違えたのであろう。そうそう、あくまで「富士の樹海」である。「富士の裾野」ではないので念のため...
2000-04-21[n年前へ]
■オレにはヤツらが見える 
スギの花粉は「見える?見えない?」
少し前まで、スギ花粉が飛びまくっていた。スギ花粉症の人にとっては、とても苦しい季節だろう。私の家族も結構スギ花粉症にかかっている。ということは、私もいつか苦しむことになるのだろう。いや、むしろブタ草を主因とする小児喘息で酸素吸入を繰り返した私であるから、まだかかっていないのが不思議なくらいである。
さて、私の勤務先でもスギ花粉で憂鬱になっている人は多い。ヒドイ(もちろん症状が)人などは、この季節になると、
「今日はスギ花粉がいっぱい飛んでいる。」と囁き始めるのである。毎日、である。そういう時に
「オレにはヤツらが見える。」
「ヤツらがオレに襲いかかってくるんだ。」
「誰かがオレの頭に電波を飛ばしてくる、という話に似ていますね。」などとチャチャを入れると大変である。
「スギ花粉症にかかっていないやつに何がわかる!」と言われてしまうのである。いや、確かに私には見えないのだ。ピンクの象が飛んでいるのが見えないように、スギの花粉も私には見えないのである。
「オマエら、スギ花粉症にかかっていないものに、所詮ヤツらは見えないんだ!」
「ほら、あそこにスギ花粉が見えるだろう」と指さす辺りを眺めても、私には何も見えない。ただ、ボンヤリした霞が見えるだけである。仕方がないので、そんな時には、なおさら
「普通の人には見えないところなんか、ホント電波と同じですね。」と言ってみたくなる。いや、私の性格からするともしかしたら言っているかもしれない。うん、言っているだろう。それどころか、
「その花粉を飛ばしてくるのは、宇宙人かナニかですか?」と、火に油を注ぐようなことを言っているに違いない。しかし、その性格は親譲りだ(坊ちゃんじゃないけれど)。
それはさておき、
「オマエら、スギ花粉症にかかっていないものに、所詮ヤツらは見えないんだ!」と言われているだけではくやしいので、私もスギ花粉を見てみたいと思う。当然である。あらゆるものを「目に見えるかたち」にするのが私の好みである。というわけで、可視化シリーズの始まりである。いや、可視化という言葉はどうも小難しく感じるので、名前を改めて「見える?見えない?」シリーズの続きである。これまで、漱石の小説、星の王子さまの内側、透け透け水着、ミニスカートの内側…などさまざまなものを「目に見えるかたち」にしてきたが、その続きというわけだ。
今回登場する、秘密道具はコイツである。
 |
この道具は、チンダル現象を利用して微粒子を可視化してくれるのだ。というと、小難しく聞こえるかもしれないが、とても簡単な原理である。光を微粒子に当ててその反射光を目で見るだけである。もちろん、微かな反射光を捉えるわけであるから、
- 微粒子からの反射光以外は目に見えないようにする
- ボケを小さくするために、絞りはできるかぎり小さくする
さて、それではコイツでスギ花粉(らしきもの)を見てみよう。暗闇に浮かぶ「スギ花粉(らしきもの)」が見えるのだ。
 |
こういった感じでスギ花粉(らしきもの)を可視化することができる。といっても、この微粒子がスギ花粉である保証は「全く」ないのであるが、あえて「スギ花粉(らしきもの)」としておくことにする。ちなみに、この画像もスギ花粉の最盛期に撮影したものである。とりあえず、こうすればスギ花粉症のあなたの敵、すなわちヤツらを目にすることができるのだ。敵であるターゲットの姿を知らずして戦うことはできないだろうから、スギ花粉症のあなたにはこの実験をすることを強く勧めたい。この画像はデジカメで撮影したのだが、実際に人間の目で見ると、ものすごい数の微粒子が飛び回っているのがわかる。今回見えた画像がスギ花粉かどうかはさておき、こういった微粒子は部屋の中ではほとんど見られない。しかし、戸外ではかなりの数の微粒子を目にすることができる。
もう一枚、参考までに示しておく。微粒子が動き回る様子が実感できるはずだ。こういう微粒子があなたの鼻や喉の粘膜に襲いかかってきているのだ。
 |
これらの飛び回る「スギ花粉(らしきもの)」を撮影したmpeg動画(115kB)をここにおいておく。スギ花粉症の人はぜひ敵であるヤツらを自分の目で確認して頂きたい。
さて、「可視化」シリーズ、改め、「見える?見えない?」シリーズはこれからも続く。ありとあらゆるものの「見える?見えない?」境界線を追求したい。どんなにクダラナイものであっても、あらゆるものを「目に見える」ようにしていきたいと思うのである。