1999-08-08[n年前へ]
■瞳の中の真実 
目の屈折率を調べよう
先日、近所の海へ行ってきた。水中メガネで覗いているとまるで熱帯魚みたいな魚が泳いでいて素敵なのだ。水中メガネを使うか使わないかで、海の楽しさは雲泥の差である。水中メガネで覗いてみると、裸眼の時とは別世界のようにくっきり見えるのである。
 |
さて、「水中視の光学」と言えば、物理の散歩道の「アユと泳ぐ」(新物理の散歩道-第2集- 中央公論社)に詳しく面白い考察がされている。本WEBでもScrapsにて「焦点」ということを考えたばかりなので、「アユと泳ぐ」と同様の解析を「できるかな?」風に行ってみたい。光学シミュレーターを作ってみたいのである。そのために、まずは人間の目の中の屈折率を調べなければならないだろう。というわけで、今回は下調べ編である。
それでは、人間の左目の水平方向の断面図を調べてみる。
 |
この中で普通のカメラでいうレンズの役割を果たしているのはどこだろうか。レンズの部分を赤く塗るとどのようになるだろうか?下に並べた3つのうちどれだと思われるだろうか。
A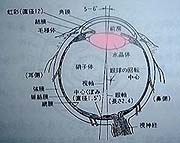 | B | C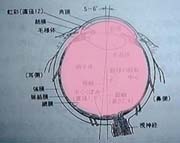 |
まずは、目の中の物質の屈折率を調べてみると、以下のようになる。
| 場所 | 屈折率 |
| 角膜 | 1.376 |
| 眼房 | 1.336 |
| 水晶体 | 1.386 |
| 硝子体 | 1.336 |
空気(15℃の乾燥空気)の屈折率はほぼ1.0であるから、空気と比較するならば、目の中の物質はほぼ同じ屈折率を持つといっても良い。角膜も眼房も水晶体も硝子体も同じ屈折率を持つとして良いだろう。すなわち、大雑把な近似においては図.2のCに示したようなピンク色のレンズがあるとして良い。つまり、目全体がレンズであり、レンズ面に焦点を結ぶようになっているのである。水晶体は若干の補正を行うに過ぎない。レンズの焦点はレンズから離れた場所にあるはずと思っている人もいるかもしれないが、レンズの表面に焦点があるものも実はよく使われている。
さて、人間が水の中に入るとどうなるだろうか?水は1.333(589.3nmの波長の光に対して)の屈折率を持つ。これは人間の目の中の物質の屈折率とほぼ同じである。水を主体として出来ている人間なのだからこれは当然だろう。しかしこれでは、目は光を屈折させることはほとんどできなくなる。そのため、水の中に入るときには水中メガネなどで目の回りを空気で満たしてやることが必要なのである。
本題からははずれるが、資料を眺めていると、面白いグラフが目に入ってきた。人間の目の断面方向の視細胞個数の分布を示したものであり、錐体と桿体を個別に示してある。「盲点」なんかも図中にある。
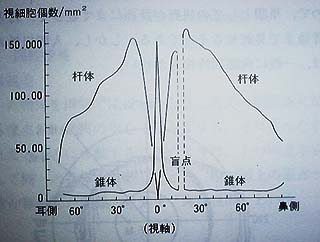 |
目に映る明るさって何ですか? - 君は天然色 - (1999.07.05)
の回に錐体と桿体については触れたが、桿体は1lx程度の暗さから働き、明るさのみに反応する。一方、錐体は10lx以上で働く。従って暗いものを見るには桿体の働きが重要になるわけだが、上のグラフは桿体が視点の中心にはほとんど存在していないことを示している。
従って、暗い所でものを見る際には、視点の中心では感度が足りなくなりやすいことがわかる。これまで、暗い星を眺めるときに視界の中心で見ようとすると見えないのだが、少し視点をずらしてやると見えるような気がしていたのだが、それは気のせいでは無かったようである。
さてさて、資料集めも終わったので「瞳シミュレーションソフトウェア」の開発に着手したいと思う。もちろん、時間がかかるのはいつものことだ。すぐにはできないけどね。
2000-05-12[n年前へ]
■メガネの内側にある歪み 
隠れたストレスに光を当てろ
また、可視化の話である。いや、自分でも忘れていたが、「可視化」改め「見える?見えない?」シリーズである。今回はメガネの内側にある「歪み」、隠れたストレスに光を当ててみたい。そして、そこに何があるかを見てみたいのである。
私の眼はどうも明るさに弱い。やたら太陽の光が眩しく感じることが多い。といっても、単に私のガマンが足りないだけかもしれない。あるいは、睡眠不足のせいかもしれない。そして、私は同時に暗さにも弱いのだが、こちらは単にビタミン不足による鳥目だろう。
そういうわけで、明るいのに弱いので車を運転する時には大抵サングラスをかけている。サングラスは何本も持っているわけだが、最近のお気に入りはこれである。
 |
これは、偏光フィルター機能付のサングラスである。偏光というギミック付のところがお気に入りの理由である。以前、
で書いたように、偏光フィルターがあれば色々なものの反射光のみを遮ったりすることができる。例えば、下の右側の写真では左の写真に比べてガラス表面の反射光が減少していることがわかるだろう。これは偏光フィルターの作用のせいである。 |  |
これと同じように、偏光フィルター機能付のサングラスを使えば色々な反射光を防ぐことができる。例えば、通常は反射光などで車のフロントグラスの内側にいる人の姿はよく見ることができない。しかし、このメガネをかけていれば、反射光に邪魔されずフロントグラスの内側を見通すことができるのである。もう、対向車なんてまるでフロントグラスがないかのようである。
この偏光フィルター機能付のサングラスは、通常「釣り」などで用いられるものだ。水面の反射光を防ぐことにより、水中の魚の姿などを見やすくするためのものである。結構、海の近くに住んでいる私にはうれしい機能である。
このサングラスをかけている時に、ふとある実験を思いついた。普段は透明にしか見えない「普通のメガネ」の影に隠れたストレスを目に見える形にしてみようと思ったのである。よく、「メガネの奥にストレスが隠れている」というが、そのストレスを見て取れる形にしようと思うわけだ。
そこで、新婚ホヤホヤの「夜の帝王」I田氏(関係ないが、I田氏から「Hirabayashiさん、小杉のメーリングリストで-できるかな?-の話題が出てましたよ。」と言われた時はビックリした。とりあえず、どなたか知らないが、メーリングリストで紹介して頂いた武蔵小杉勤務の方には一言お礼を言っておきたい)にメガネを借りてみた。このメガネをじっくり眺めてみてもらいたい。
 |
この透明なメガネの奥に何か見えるだろうか?そこに「歪み」は見えないだろうか?「透明だから、何も見えないだろう。」という人もいるだろうが、あるグッズを使うと、もう明らかに見えてくるのである。それが、下の写真である。レンズを固定している辺りをよく見てもらいたい。不思議な
虹模様と十字の模様が見えるはずだ。
 |
プラスチック等は製造過程での不均一な応力や、外力により複屈折性を示す。光弾性と呼ばれる現象である。そのため、偏光面を直行させた偏光フィルターの間にそういうプラスチックなどを挟みこむと、その弾性体の内部に働いている応力分布の状態を調べることができる。それを応用したのが、偏光顕微鏡などである。
例えば、下の写真はカセットテープのケースの左側部分を、偏光面を直交させた二枚の偏光フィルターで挟んでみたものである。見事に弾性体の内部に働いている応力分布が可視化できているのがわかると思う。これを応用すれば、例えば熱変形をしているようなものであれば、透明体の熱分布も簡易的に見て取ることができる。
 |
そういうわけで、先の写真あるいはそれを拡大した次の写真のように普通では見えない透明なプラスチックレンズの中に隠れている「ストレス」を見て取ることができるわけだ。
 |  |
とりとめもないが、今回は透明なメガネの影に隠れたストレスに光を当ててみた。ちゃんと見ようと思いさえすれば、目に見えるものは数多くある。「見える?見えない?」の境界線はその人自身が決めるのである。「できるかな?」では、これからも色々な「見える?見えない?」を追求し、「見えるかな?」について考えていきたいと思う。
2000-06-29[n年前へ]
■オッパイ星人の力学 
胸のヤング率編
本WEBサイトは「技術系サイト」というジャンルに分類されることが多い。が、実際にはどうも変な話題も多いように思う。しかし、私の観察によれば技術系サイトと呼ばれるところには必ずこの手の話が転がっているのである。実際、究極の技術系サイトの「Fast&First」でもというような素晴らしい話題はいっぱいあるし、同様に至高の技術系サイトである「今日の必ずトクする一言」の中でもという絶品の作品達が飾られている。
いや、つまり何が言いたいのかというと、変な話を書いてしまったことを正当化したいのである。技術系サイトには「とても身近なナゾ」への探求話が欠かせないのだから、変な話を書いたけど、勘弁しておいて欲しい、と言いたいのである。間違ってもエロサイトには分類して欲しくないのである。さて、どんな話かは下を読んで頂くことにして、もう少し言い訳を続けたい。何と言うか、この話を書き終えて何故か言い訳なしにはWEBに出せないような気持ちに、私はなっているのである。いっそのこと、この話は封印しようかとも考えた。しかし、先に示したように究極・至高の技術系サイトにもこういった?類の話があることに勇気付けられ、せっかくなので公にしてみることにした次第である。
以前、
で「できるかな?」読者の好みを調べてみた。それがこの下の円グラフである。 |
この円グラフから引っ張った部分は「エロ」である。これは、「IO = アイオー」ではない。「エロ= えろ=すけべぇ」である(前にも書いたけど)。 かように、「エロ」に興味を持つ人は多い。例を挙げるならば、「オッパイ星人」という言葉があるくらい、男の中には女性の胸に興味を持つ人が多い。私の友人の中には、ことあるごとに「おぉっ!!」と言いながら、通り過ぎる女性の胸を眺めるような輩までいるのである。しかもメガネをポケットからすばやく取り出し、サッとメガネをかけながら眺めるのである。まるで、ウルトラマンのセブンに変身する瞬間のモロボシダンなのである。「ウルトラセブンか、オマエは!」とか「モロボシダンがオッパイ星人に変身してどないすんねん!」と突っ込みたくなるほどである。
とりあえずこういう「オッパイ星人」のために、今回は「オッパイ星人の力学」について考えてみたい。具体的には、「バスト(なんか気恥ずかしいので言葉を変えた)の力学」について考えてみることにした次第である。
それでは、バストの力学について考え始めることにしよう。今回は、まずバストの基礎特性を調べ、次回にその運動力学について考えてみる予定である。
最初に、基本的な知識からだ。TVを観ていると、よく「Fカップアイドル」というような言葉を聞く。その言葉はよく耳にするのだが、実際のところその意味は知らなかった。そこで、調べてみると、ブラジャーのカップサイズは次の表のようにして決まるという。
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| アンダーバストと トップバストとの差 | 5.0 | 7.5 | 10 | 12.5 | 15 | 17.5 | 20 | 22.5 | 25 | 27.5 | 30 | 32.5 | 35 |
胸のバスト直下の部分の胸囲 = 「アンダーバスト」と、バスト部分の胸囲= 「トップバスト」の差からブラジャーのカップサイズが決まるわけだ(って今知っただけの知ったかぶりだけど)。Kカップなんてのもあるなんて驚きである。いやぁ、知らなかった。
しかし、「アンダーバストとトップバストとの差」が判っただけではバストの力学について考えるのは難しい。もう少し、取り扱いやすい量に変形させたい。そこで、次のような図を考えてみた。これは「胸部の断面図」である。上方向が人の前面方向である。
 |
バストを「半球状の物体」と仮定して、その「半球の半径 = r」を計算したいのである。そうすることで、バストの形状を計算しやすくなるのである。現実問題としては、バストがそうそう「半球状の物体」になるわけはないだろう。しかし、今回はとりあえず理想のドーム形状のバストを計算してみる、ということで許してもらいたい。
さて、上の極めて大雑把な近似をしまくりの図を見て頂くと判るように、
アンダーバスト = 4r + 4r + 2 胸のベース部分の厚さであり、
トップバスト = 2 r + 2 π r/2 + 4r +2 胸のベース部分の厚さである。したがって、
「アンダーバストとトップバストとの差」 = ( 2 r+2π r/2+4r+2胸のベース部分の厚さ)と計算してやることができる。そのようにして、計算した「胸のカップ数とr(cm)」を示したものが下の表である。ただし、実際には胸囲はそもそも下へ行くほど小さくなっているだろうから、アンダーバストはトップバストよりも胸のベース部分が35%小さいとして計算してみた。
- ( 4r+4 +2胸のベース部分の厚さ )
=2 r+2πr/2-4r
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| r | 2.8 | 4.3 | 5.7 | 7.1 | 8.5 | 10 | 11 | 13 | 14 | 16 | 17 | 19 | 20 |
これをグラフにしたものを下に示す。ほぼ直線的にバストのサイズが増加しているのが判ると思う。
 |
例えば、AAAカップだと半径2.8cmの半球状の物体だ。まるで、スーパーボールである。これなら、ブラジャーはいらないだろう。それが、Kカップともなると半径20cm程になる。ちょうどメロンを半分に切った感じだろうか?これはかなり、デカイ。
このr(cm)さえ計算できれば、あとは物体形状も体積もわかる。体積が判れば、当然のごとく重さも計算することができる。というわけで、次は重さについて考えてみよう。何しろ、バスとの運動力学を考えるならば、どの程度の質量を持つかどうか考えることは避けて通れないのである。
バストのほとんどの部分を占めるのはきっと脂肪だろう。脂肪の密度は水とほぼ同じだろう。そこで、脂肪の比重が1g/cm^3であるとして計算してやると、「胸のカップ数と胸一個あたりの重さ(g)」は以下のように計算することができる。(実はこの計算には後の松坂季美子の胸の重さに合わせるための定数、季美子定数を乗してある。)
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| 胸一個あたりの重さ(g) | 8.9 | 30 | 71 | 140 | 240 | 382 | 570 | 810 | 1100 | 1500 | 1900 | 2500 | 3100 |
なんと、Kカップでは「胸のカップ数と胸一個あたりの重さ(g)」が3000g= 3kg程もあるのだ。新生児が二人胸にぶら下がっているのである。この数字がホントなら大変な話だ。肩に負担がかかりんまくりである。1.5リットルのペットボトルを4本も胸にぶら下げているのだから、これは大変だ。なるほど、ブラジャーは必需品である。
上の表をグラフにしたものが下である。
 |
バストの質量は体積に比例する、すなわち、バストのサイズ( =長さ )の二乗に比例する。そこで、このような形状のグラフになるわけである。このグラフを眺めていると、Dカップ辺りを境にして、それより大きくなると胸や肩にかかる負担がシャレにならないくらいの大きさになると推測される。
ところで、地表にいる限り、当然バストも重力の影響を受ける。いや、むろん地表でなくても重力の影響は及ぼされるわけだが、そういう話は今回はおいておく。とりあえず、六本木を歩いている彼女も、ロサンゼルスにいる彼女も重力の影響を受けるのである。重力を受ければ、当然バストは重力で引っ張れる方向に垂れ下がってしまう。その様子を示したのが、次の図である。ここでは、「胴体から垂れ下がるバスト」を単純に「重りとバネで表すことができるモデル」だとしてみた。
 |
さて、一般的にバネの特性はフックの法則により
ここまで来れば、あともう一歩である。この式のkすなわち「バストに関するヤング率」を調べるだけである。「バストの垂れ具合」と「バストの重さ」を同時に計ってやれば良いのである。そうすれば、残るただ一つの変数、「バストに関するヤング率」を計算することができる。いやぁ、簡単、簡単....
といっても、実際のところここが一番苦労した。「バストの垂れ具合」と「バストの重さ」を同時に計らせてくれる人なんかどこにもいないのである。当たり前である。
そこで、ネットで検索をかけまくること数時間、ついに私は見つけたのだ。
そして、その質量 一個1kg!」
科学の徒として、私が丁寧に観察した結果、松坂季美子の「バストの垂れ具合」は約10cmであることがわかった。いや、もちろん科学の探究心のためであって、それ以外の気持ちはなかったことをここに誓っておこう。
その苦労の結晶のデータが、
- 松坂季美子はGカップ、バストの重さ=1kg、バストの垂れ具合10cm
この境界条件さえあれば、「バストに関するフックの法則」を完全に解くことができて、「バストに関するヤング率」も導き出すことができるのだ。ちょちょいのちょい、である。
その「バストに関するヤング率」を用いて計算してみた「胸のカップ数とバストの垂れ具合(cm)」を次に示してみる。
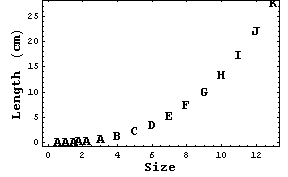 |
バストの「カップ」サイズの三乗に比例して、「バストが垂れていく様子」がよくわかると思う。この物理形状は「カップ」サイズに比例して、「バストの垂れ具合」は「カップ」サイズの三乗に比例するというデータを用いることにより、「究極のバストサイズ」を導き出せるのではないか、と私は考えているのである。が、それはまたいつかの話題と言うことにして、話を続けたい。
ところで、「バストに関するヤング率」は常に一定ではない。「おばあちゃんの垂乳根」を想像して頂けばわかるように、年をとれば「バストの垂れ具合」は大きくなるのである。
というわけで、さっきの計算結果をもっと若い条件、すなわちもっとヤングなヤング率で計算してみたのが次のグラフである。
 |
赤のもっとヤングなヤング率で計算してみた場合には、バストには張りがあって、バストの垂れ具合は小さいことがわかると思う。
さて、今回はバストの基礎特性を調べてみた。次回、この「バストに関するフックの法則」を用いて、「オッパイ星人の動力学」について考えてみたい、と思う。
追伸 : この話を書き上げた後に、恐る恐る回りの人に感想を聞いてみた。すると、
と言われてしまいました。ハイ、申し訳ありません。その通りでございます。返す言葉もありません。「こんなの作るくらいなら、
男の人のヤング率でも計算しなさいよ。」
2002-06-03[n年前へ]
■カードサイズの「画像探偵セット」!? 
お手軽線数メーターを作るのだ
「どんなものでも、自分の目で眺めてみた〜い」と、ワタシはいつでも思う。世の中スベテのものを、自分の目で眺めてみた〜いと思う。しょんべん小僧が空中に描き出す放物線、巨乳ギャルにロックオンするオッパイ星人の目の動き、ビデオにかかるモザイクの向こう、はたまた田代まさしが恋い焦がれるミニスカートの結界の秘密、とにかく世の中のものスベテを何でもかんでも眺めてみたい、覗いてみたい、とワタシはいつも思っているのである。(とはいえ、誤解されると困るので念のために書いておくが、もちろんミニスカートの中を覗いたりはしないのだ)
そんなわけで、ワタシのケータイのストラップには「ちっちゃなちっちゃな虫メガネ」がついている。この虫メガネを武器にして、ワタシは色んなモノを覗くのがクセになっている。スーツ姿で出張している時だって、おもむろにこの虫眼鏡を取り出して、色んなものを覗いてみたりしているのである。
 |
だから、毎朝届けられる新聞に折り込まれているチラシやカタログを眺めるときだって、そんなカタログに「ちっちゃなちっちゃな虫メガネ」を向けてみて、その「虫メガネ」を通して、カタログがどんな風に印刷されているかをよく眺めてみる。下の左のようなカラーの綺麗なカタログだって、「虫メガネ」を通して眺めてみると、右の拡大写真みたいに、四色(シアン、マゼンダ、イエロー、ブラック)が規則正しく並んでいるようすが見えてくるのである。離れてみればキレイな写真が「虫メガネ」を通して眺めてみるだけで、こんな風に様子が変わるなんてとても不思議な気分になったりするのである。まるで、女性の化粧のように不思議で、こんな四色の手品はとても面白いのである。
| (左上と右上部分はマゼンダとシアンだけを見やすくしてみた)
|
で、こんなカタログの拡大図を眺めていると、四色に分けられた色がどんな風に並べられ形作られているかを、知りたくてたまらなくなったりする。つまり、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とか思うわけである。もちろん、この画像に二次元フーリエ変換などをかけさえすれば(周波数解析をすれば)、「どんな角度で・どんな間隔で色が並べられているか」ということは知ることができるけれど、まさかワタシの頭の中でそんな作業ができるわけはない。かといって、このカタログを読み込むための「画像読みとり装置」や「解析をするためのコンピューター」を毎日持ち歩くなんてこともできるわけもない。
そこで、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とかいう疑問の答えがすぐ判るように、先日こんなカード、ぴったりクレジットカードサイズの透明シートに規則的なパターンを印刷したカード、を作ってみた。名付けて、Peco-Chartなのである。
これはもちろん、判る人には判るだろうが、ハンディ「線数メーター」というモノである。一言で言えば、画像の周波数解析をとっても簡単にすることができる手品の小道具のようなカードなのだ。
 |
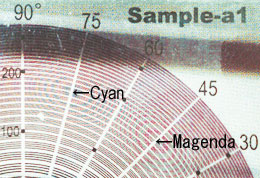
例えば、さっきのカタログの上にこのPeco-Chartを重ねて置いてみると、アラ不思議、何やらヘンな模様、不思議なモアレ模様が浮かび上がってくる。下の左の写真、あるいは右の拡大写真を眺めてみればマゼンダとシアンの同心円がハッキリと浮かび上がっているのが見えるだろう。例えば、シアン色の場合は75°の角度で175線(175線/inch)位の位置、そしてマゼンダ色の場合は45°の角度で同じく175線位の位置を中心として、同心円状のモアレ模様が浮かび上がっている。
つまり、「このカタログはシアンは75°の角度方向に1インチ辺り175個のドットが並べられていて、マゼンダのドットは45°の角度方向に並べられている」、ということを、このPeco-Chartを重ねて置いてみさえすればたちどころに知ることができるのである。
 |  |
 |
こんなペラペラのカードで周波数解析ができるなんてとても不思議に思えたりもするけれど、ちょっと考えてみればこれはごく当たり前の話である。
でも似たようなことをしたように、モアレというものは「二種類以上の何らかの模様(パターン)が干渉して発生する」ものである。つまり、ある意味「二つのパターンの相関をとる」ということである。そしてまた、少し考えてみれば「画像の周波数解析」というものは「対象となる画像」と「基準関数(三角関数etc.)」の間で相関を調べることと同じである。だから、「基準となるパターン」を「対象となる画像」の上に重ねてみた時に見えるモアレのパターンは「対象となる画像」の周波数解析結果を実は示していると考えてみても良いのである。だから、このPeco-Chartはクレジットカードサイズのペラペラなちっぽけなヤツではあるのだけれど、実は色んな画像の周波数解析をしてくれるスゴイヤツだったのである。そして、こんなポケットに入るほど小さい線数メーターははなかなか無いので、、カード入れからコイツを華麗に取り出してみせたりすると、うらやましがる人もとても多く(仕事柄、画像出力に関わる人達が多いから)、なかなかに気持ちが良いのである。 とはいえ、自慢してばかりでは何なので、さらに大量に配布すべく新たなPeco-Chart二号機をデザインしてみた。それが、下の名付けてPecochartproである。
 |
このPecochartproの謳い文句はその名の通り「プロ仕様」というわけで、画像出力に関わっている何人ものベータテスター達(自分も含めて)の感想をもとにして、
- 70線から350線までの線数とスクリーン角度の測定ができる「線数・角度メーター」(分解能を2線単位から1線単位へと二倍向上、スクリーン角度のガイドは2.5度刻み)
- 90線から410線までの線数を高精度(0.25線刻み)に計測することができる「線数メーター」(新機能)
- 線・文字の太さを計測できる「線幅スケール」(新機能)
- 〜30級、〜30ポイントまでの文字サイズ(級数、ポイント)測定ができる「文字スケール」(Peco-Chartと同じ)
- 「8cm定規」(Peco-Chartと同じものを使い勝手はそのままにコンパクト化)
- そして、便利な「画像に関する換算表」(内容を従来比75%増量)
それにしても、何か自分に役に立つツールを作るというのは本当に楽しい作業だった。手作りツールぎゃらりい脇色彩研究所ではないけれど、こんな「hirax.netオリジナルグッズ」をいっぱい作って「探偵セット」ならぬ「できるかな?セット」として、面白メールをくれた方にプレゼントとかしてみたら楽しいんだろうなぁ、と思うのである。というわけで、そんなツールをせっせと作るのだぁ、なんてことを実は計画中なのでした、ハイ。
2003-04-13[n年前へ]
■The Geometry of Japanese Schoolgirls 
けんさんとChicさんからのツッコミでThe Geometry of Japanese Schoolgirlsを見に行って、足跡を残してくる。といっても、外国語が心底苦手なワタシだから、本当に足跡だけになってしまうのが情けないのである。けんさんとかChicさんの方がよっぽど英語が…(以下略)と言いたくなるのである。
しかしなんだ、日本人のイメージが、オッパイ星人だとか、スクール水着だとか、メガネっこだとかね、ホラとんでもないイメージになっちゃうなぁ。日本人の面汚しって言われるのかなぁ。いや、否定はしないけど。
とにかく、そんなイメージでも「それを読みたいから日本語を勉強したい」っていうのが…素晴らしい…かも…!?
