1999-03-30[n年前へ]
■ペットボトルロケット 
天まで昇れ
-天まで昇れ-
先日、2月21日、糸川英夫が死去した。ロケットを研究し続け、日本のロケット技術を築き上げた人である。
ISAS(宇宙科学研究所)の歴史(http://www.isas.ac.jp/info/history/index-s.html)
そこで、私たちが簡単に打ち上げることのできる、ペットボトルロケットについて考えてみたい。ペットボトルロケットは素晴らしい科学おもちゃだ。ロケットが大気中を飛ぶときと、宇宙空間を飛ぶときの原理の違いを的確に体現していると思う。それは、ペットボトルの中に水を入れてあることだ。ペットボトル中に水を入れることで、革命的ないくつかの効果があると私は思う。挙げてみると、こんな感じだ。
- 空気と水の粘性の違い->水の方が長時間にわたり一定の噴出量にしやすい。
- 気体(空気)と液体(水)の圧縮性、質量の違い->
- 空気を噴出する場合には、ロケットの前後の圧力差が推進力を支配する。
- 水を噴出する場合には、反作用力(運動量保存)が推進力を支配する。
空気のほうは温度が違うと結構違う。摂氏0度で1.293kg/m^3であり、100度で0.946kg/m^3である。もちろん、気圧が違えば、それに比例して体積は大きく変わる。
結局、空気と水とでは質量が約1000倍違う。だから、ペットボトルロケットが後ろから水を噴出する場合には、空気の場合に比べて、1000倍もの反作用力を受けるのである。つまり、ロケットは1000倍の推進力を持つことになる。ただし、空気の場合には、ペットボトル中で数気圧分圧縮されているので、質量も数倍になる。したがって、正確には1000倍の数分の一ということになるだろう。
逆に、ロケットの前後の圧力差を考えてみる。、空気の場合には、前後で数倍の圧力差が生じるだろうが(WEBで調べると5-7倍位が通常上限のようだ)、水の場合には前後での圧力差はほとんどないだろう。だから、水を噴出する際にはこれによる推進力はほとんど働かないだろう。しかし、空気を噴出する際にはこの圧力差によりロケットは進むことになる。真空中ではこの方法では推進力はほとんど働かない。
こういった違いをもとに子供(といっても高校生位か)に宇宙でのロケットの原理を説明すると面白そうだ。これら推進力の違いは、とても大きいと思う。
かつては、セルロイドを使った小さなキャップロケットの時代だった。今は、ポリエチレンテレフタラート製の大型ロケットの時代に変わった。
今日は久しぶりに雪が降った。「雪は天からの手紙である」と言ったのは、雪を研究し続けた中谷宇吉郎だった。ならば、私たちが打ち上げるペットボトルは天へと届けるロケットだ。空へ高く届くように、私たちはそれを打ち上げ続ける。いつか、私たちのロケットは天へ昇る。
 |
1999-11-13[n年前へ]
■やっぱり、ウニが好き ! 
Dr.フラーはウニの夢を見るか?
私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。と、始めると
の間違いと思われるかもしれない。しかし、それは違う。今回は、ウニとドームハウスの共通点について、考えてみたい。ただ、かなりビールが脳みそにしみているせいか、少しドンデモ話になるかもしれない。そこは、「ビックエッグの力学」と共通である。 私の中では、野球観戦と言えば、ビールだ。野球にはビールが良く似合う。そして、今現在も目の前にはビールがある。そして、寿司がある。といっても、スーパーで買った安物である。二つ合わせても1000円にしかならない。
 |  |
安物といっても、私の住んでいるのが港町だから安い、ということもある。何しろ、ほとんどのスーパーの魚売り場でイルカの肉なども置いてあるのだ。嘘ではない。ホントにホントである。私も、引っ越してきた当時はビックリしたが、本当である。アメリカの動物愛護団体が見たらびっくりの風景だろう。「イルカと人間はお友達」と言ってる人には見せられない風景だ。
あまりおいしそうではないので、私はまだ実際に味わってはいない。しかし、地元の人の中には「よく食べる」と言う人もいる。いつか、挑戦してみたい。
さて、上の写真で共通しているのはウニである。ウニと言えば、こんな姿をしている。
 |
「海栗」と書いてウニと読むことが実に納得できる姿である。しかし、内面はもう少し違う。実は、ウニはドームにそっくりである。前回考えたドーム球場ではないが、ウニは実はドーム構造をしているのだ。「そんなことは当たり前じゃないか」と言う人もいるだろう。しかし、私はつい最近までそれを知らなかった。そもそも、骨があるとすら思っていなかったのである。
もしかしたら、私のようにウニの内面を知らない人もいるかもしれない(そんな人はいない、という声も聞こえそうだが)。そこで、ウニの骨の写真を示してみる。下に示すのが、色々なウニの骨だ。
 実物はとてもきれい。日本古来の木工細工のような穴がとてもきれいである。 |
これは少し前に、宇宙科学研究所の黒谷氏の実験室を見学(ただ邪魔しただけという気もするのであるが)する機会があり、そのとき頂いたものである。最初に見たときは、「目からウロコ」であった。まさか、あの針の山の下にこんな頑丈な殻が存在しているとは、思わなかった。
写真ではわからないかもしれないが、骨には小さな穴が極めて規則的に開いている。それが、日本古来のとても出来がいい木工細工のようである。光に透かしてみると、うっとりするようなきれいさである。内部に強い光源でもおけば、プラネタリウムやミラーボールみたいに細い光線を放射する、きれいなアクセサリーができそうだ。
ところで、「何故、宇宙科学研究所の実験室にウニが?」と思われる方は、WEBで検索でもかけてみると良いかもしれない。「宇宙生物学」という面白い実験分野があるものだ。
例えば、無重力の中で生物がどのような挙動を示すか、などの研究をしたりするらしい。飛行機にのってそういう実験を繰り返すわけである。遊園地のフリーファールやバンジージャンプ、そして、ジェットコースターでさえ、駄目な私には地獄のような研究分野である。
さて、上の、ウニの骨の姿はまさにドームそのもの、とは思えないだろうか? そう、似ているのだ。 そっくりなのだ。試しに、このドームなどを見れば納得できるだろう。
 |
これは、富士山頂の厳しい環境を耐えるために、極めて安定なドーム構造が用いられているのだ。三角形のパネルが組み合わさるドームハウスは極めて頑丈である。ウニも、同じように頑丈なドーム構造の骨格を持っているのである。レーダードームは富士山頂で頑張っているが、宇宙科学研究所のウニは色々なところへ連れて行かれて、厳しい実験に耐えているのである。
こういった、ドームと言えば、R.バックミンスター・フラー博士のドーム理論だろう。フラー博士とドームハウスのスケッチ図を示してみる。
|
よく、環境適応性の高さを謳うことの多いドームハウスであるが、もしかしたら、ウニがその祖先であるかもしれない。もしかしたら、フラー博士は「海の中でじっとたたずむウニの夢を見て」ドームハウスを思いついたのかもしれない。
アメリカ人であるフラー博士がウニを食べたとは思えない、という人も多いだろう。それは確かにその通りである。しかし、フラー博士はかなりの変人である。変人ならば、ウニを食べまくっていたとしても、おかしくはない。
普段は「何を馬鹿な発想だ」と思うことだろう。しかし、ドーム球場の野球を見ながら、脳みそがビールとウニで満たされてしまうと、「そうだ、フラー博士はウニが大好きなのだ!そうに違いない!」と確信してしまうのだ。
仮に、フラー博士がウニに影響されていないとしても、ウニはフラー博士がドーム理論を考えるずっと太古の昔から、ドーム構造をしていたのである。ならば、「元祖はやはりウニなのだ!」と言ってしまって良いだろう。太古から厳しい環境を耐えつづけてきたウニは、今や宇宙へ飛び出し、さらに厳しい環境の中で活躍しているのである。
2000-05-13[n年前へ]
■ミウラ折りの落書き紙 
思ったことを折り込めて
十年位前のことだったと思う、「知人の先生がこんなのを作ったんだけど、興味あるだろう?」と父が不思議な冊子を私にくれた。冊子と言っても、それは一枚の紙を折り畳んだ小さな小さなものだった。ちょっと面白い折り畳み方をされたその紙には、その折り畳み方の説明とその「折り畳み方」の応用が書かれていた。もちろん、その冊子の作者は宇宙科学研究所の三浦教授で、そしてその冊子の折り畳み方はあの有名な「三浦折り」である。
三浦折りの折り目を示してみると、例えば下の図のようになる。一目見てわかるように折り目が直交していない。そのため、それぞれの折り目が独立でなく、全ての折り目が同期しているのである。言い換えれば、一つの折り目を開こうとすると全ての折り目が開いていくし、一つの折り目を閉じようとすると全ての折り目が閉じていく。だから、例えば、折り目の端っこと端っこを掴んでただ引っ張れば全ての折り目が開き、そして折り目の両端を縮めれば自動的にパタパタと折り畳まれていくのである。
また、折ってみるとわかるのだが、この三浦折りは折り目が少しづつずれて重なるのである。折り目というのは厚みが他の部分に比べて厚いために、折り目が重なるとその部分だけがどうしてもかさばってしまう。しかし、この三浦折りであればそんな折り目が重ならないので、折り畳んだときにかさばらないのである。
 |
だから、太陽電池パネルなどをこんな三浦折りを使って折り畳むと、折り畳んだときにはかさばらないし、その展開や収納は隅と隅をただ引っ張ったり縮めたりしさえすれば良い、というわけで良いことずくめというわけだ。詳しくは、宇宙科学研究所のここ辺りを読んでもらうことして、参考までにそこの画像にリンクを張っておく。
 |
ところで、十年前に父からもらった「三浦折りの冊子」を捨てるはずはないから、部屋のどこかに隠れているとは思うのだけれど、何処かに隠れてしまっていて、見つけることができなかった。私の部屋が三浦折りのようになっていて、部屋の隅から隅までを全て引っ張り出すことができたら、きっとすぐにでも見つけられたのだろう。しかし、残念ながら私の部屋は三浦折りではないのである。だから、私の色々なモノや本が散らばった部屋に隠れている「三浦折りの冊子」はそう簡単に見つけられるわけもない。
そういえば、ふと何かが心に思い浮かぶことも日頃よくあることである。しかし、思い浮かんだその時に書き留めておかないと、すぐに記憶の何処かに隠れてしまって忘れてしまうことも多い。これもまた、私の記憶が三浦折りだったらよいのだろうけれど、幸か不幸か私の記憶システムは三浦折りではない。私の記憶や考えたことが三浦折りのようにパタパタ開かれていくのも見てみたい気もするけれど、隠しておきたいような夢や気持ちもあるだろうから、やはり私の記憶システムが三浦折りでない方が良いのだろう。
とはいえ、やはり後で思い出したいこともたくさんあるわけで、そんなことは思い浮かんだらすぐに何かに書き留めておかなければならないだろう。落書き帳か何かに、思い浮かんだことをすぐに書き留めておけば良いわけである。適当な落書き帳に書き留めれば、思い浮かんだことを忘れてしまっても安心である。
しかし、頭に何かが浮かぶ瞬間というのは、時間や場所を選ばないだろうから、そんな落書き帳はいつも持ち歩かなければならないだろう。となると、いつも持ち運ぶためにはコンパクトでなくてはならないし、そんな落書き帳を広げる作業は簡単に素早くできなければ不便である。だとしたら、その落書き帳はまさに三浦折りを使うべきではないだろうか? というわけで、私は自分用の「落書き紙」をミウラ折りを使って作ってみることにした。
というわけで、作ってみたのがこの「できるかな?」特製「落書き紙」である。折り畳んだ状態は三浦折り特有のちょっと不思議な重なり方になり、見た感じのデザインも割に良い感じだと思う。そして、これが「できるかな?」特製「落書き紙」折り畳みのようすである。
両端を動かすだけで、パタパタと自然に開いたり折り畳まれていくようすがよく判ると思う。 | 実際の大きさは掌にすっぽり隠れるサイズ。 裏表紙は表紙を裏返したデザイン。それは、考えたり思ったりしたことにはきっと表も裏もあるだろう、という気持ちの現れなのである。 |
ここにPDFファイル化した「できるかな?」特製「落書き紙」を置いておくので、興味のある人はぜひプリントアウトして三浦折りを実際に試してみると面白いと思う。このPDFファイルは開くときにパスワードを聞いてくるが、"hirax.net"といれてやれば開くことができる。
ちなみに、この「できるかな?」特製「落書き紙」の表と裏を見てみるとこんな感じになる。裏表紙は表紙をそのまま裏返したデザインにしてある。それは、考えたり思ったりしたことにはきっと表も裏もあるだろう、そしてそれは表裏一体で単に裏表の関係なのかもしれない、という気持ちの現れなのである。 |
 |
この「できるかな?」特製「落書き紙」の作り方であるが、まずこのPDFファイルを長手綴じで両面印刷をする。そして、上下左右マージンが不揃いであれば、端部を少し切り取る。実際に折り畳んだ後であれば、そのどの程度不揃いなのかがわかりやすいから、端部を切り取る(切り取らなくても良いが)のは一番最後でも良いだろう。
そして、表の面の折り線に沿って、次の写真のように折り畳んでいくのである。
|  |
 |  |
さて、この三浦折りの「できるかな?」特製「落書き紙」は折り畳めばとても薄く小さいから、ポケットに入れていつも持ち歩いて、心に浮かんだことなどを書きとめて持ち歩くのに最適だと思う。そして、この落書き紙の裏や表に、思ったことの表から裏までを書き留める。そして、そんな思い・考えの切り抜き・断片、を小さく折り畳んだまま伝えたい人に手渡してみて、折り畳まれたもの達がその人の掌の中でパタパタと現れてくるのも、それはそれで不思議に新鮮な感覚だろう。例えば、ちょっと不思議な「三浦折りのラブレター」なんて、不思議でいい感じだと思うんだけれど… 駄目かなぁ?
2001-01-13[n年前へ]
■オッパイ星人の力学 第四回 
バスト曲線方程式 編
先日、父から封書が届いた。二十一世紀にもなったというのに、e-mailでもなくて封書が届いたのである。これは、やはりアレだろうか。いい年にもなってるのに、クダラナイWEBサイトを立てているデキの悪い息子を厳しく叱るためだろうか?しかも、そのクダラナイWEBサイト(しかも、有害公式認定サイト)の名前が自分の名前(hirax)だったりするからだろうか?それとも、「本が出たなら送れ」とは言われても実は送りたくなかった「あの本」を、少し前に父に送ってしまったからだろうか?いや、それとも…そんなこんなでドキドキしながら封筒を開けると、記事のコピーが二つ入っていた。他には何も入っていないのである。一体これは何の記事だろう?と思いながらそのコピーを眺めてみた。すると、まずひとつは去年の12月25日付けの毎日新聞の科学欄である。二十一世紀を専門家達が予想した記事の横に「究める」というコーナーがあって、そこに「女性の胸と男性の好みの進化的関係は?」というインタビュー記事があった。そして、その記事が蛍光ペンでマーキングしてあったのである。
これは一体、どういうことなのだ?と頭の中がグルグル&複雑な気持ちになりながら、とりあえずその記事を読んでみた。すると、この記事がとても面白い。インタビュー中の
ヒトは異性をどう選ぶのか?そんな疑問から女性のバストと弾性の好みに進化的関係があるかを研究している。という東大大学院の東海林さんの語りもとても面白いし、バストサイズを5段階に変えた女性の合成写真を使い、男子学生300人にアンケートしたという実験とか、巨乳好きの性格が父から受け継いだものであるかを調べるために、父子間で性的好みが伝達されるかを調べる、などの話もとても面白い。最高である。(中略)小さいバストほど魅力的だと母に教えられて育った。しかし、大きいバストが好きな男性がいることに気付いて驚き、「なぜ」と考えたのが研究のきっかけだった。(中略)「大きいバストが本当に普遍的に好まれるかを知りたい。控えめなバストが淘汰されてしまうとは考えたくないから」と話す。
そして、父からの封筒に入っていたもう一つの記事は宇宙科学研究所の新聞の中の宇宙基地利用研究センターの黒谷氏の「Anti-Gravity」というエッセイだった。なんでも、Anti-Gravityという化粧品があって、
それは顔の皮膚のコラーゲンに皮膚がたるまないようにするというものらしい。顔の皮膚にハリをあたえて、顔のたるみを防ぐのである。顔の皮膚のたるみ元をたどれば重力のせいだから、「anti-gravity= 無重力」化粧品ということになるわけだ。じゃぁ、このAnti-Gravityを体中に塗れば、バストやヒップが垂れるという女性の悩みもなくなるのではないか、と「無重力における生物の専門家」である黒谷氏は書いていて、参考文献に本サイトが挙げられていたのである。
うむむ、世の中には巨乳の科学について進化論的に研究している人がいたり、オッパイの力学について考え(てみたりもす)る無重力生活の専門家もいるのだ。これはマズイ。油断している場合ではない。私もオッパイ星人研究をもっと真剣にしなければならない。父はきっと私に「研究の厳しさ」を教えようとしたに違いないのである。私の父はこれまでの「オッパイ星人の力学」を読んで、美味しんぼの海原雄山風に「うわあっはっ、こんなものでオッパイ星人の力学だとは笑止千万!」位のことを言ったに違いないのである。
しかし、それだけではない。「二十一世紀、小さいバスト、大きいバスト、無重力、皮膚、オッパイのたれ」というヒントを与えてくれたのである。ここまでされて何かを書かなくて何としよう。オッパイ星人研究の手は一瞬たりとも休めてはならぬのである。そこで今回は「皮膚のハリ」や「重力」を気にしながら、「オッパイのたるみ・形状」について考えてみることにした。
さて、一体バストの形状というものはどうなっているのだろう?これまでの「オッパイ星人の力学」では
- 半球モデル
- 円錐モデル
そしてもちろん、このモデルに対して不満を持つのは私だけではなくて「これらのモデルには私は納得できません。」というメールがたくさん送られてきた。それどころか、「本当のオッパイをあなたは知らないのではないですか?」という実に失礼?なメールさえ送られて来ていたのである。「それでは、参考までに本当のオッパイの資料でも送って頂けないでしょうか?」とは私は大人なので返事をしなかったが、ちゃんとしたモデルを作らないことにはこれからもそんなメールがまだまだ来るに違いないのだ。
というわけで、今回は新しいバストの形状モデルを提唱してみたい。それは「バストの内部は液体に満ちていて、その液体を外側の皮膚が支える」という
- 水風船バストモデル
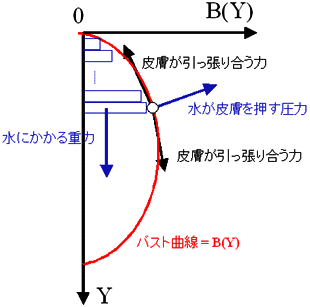
こんなモデルに基づいて、バストの形状を計算するにはどのように考えれば良いだろうか?次の図が「水風船バストモデル」における内部の水と各皮膚部分にかかる力を示してみたものである。これはバストの断面をを鉛直方向に示しており、左の黒い鉛直線が胸板であり、赤い線がバストの形状を示すバスト曲線である。(ちなみに、今回はバストを二次元の断面でのみ考えている。)
赤い線がバストの形状を示すバスト曲線
|
「水風船バストモデル」における内部の水には重力がかかり、バストの下の方にいくほど圧力がかかっている。そして、皮膚に面している内部の水はその圧力を皮膚に伝える。そして、皮膚はその圧力で変形しながら水で満ちたバストを支えるのである。この時、バストの形状= 皮膚の形状を示すバスト曲線はどんな条件を満たしているだろうか?
ここで、胸板にそって下向きにY軸をとり、バスト曲線をB(Y)で表すことにしよう。上の図をよく眺めるとわかると思うのだが、バストの形状= 皮膚の形状を示すバスト曲線をB(y)とすると、バスト曲線B(y)は実はこんな方程式を満たす。
 |
まぁ、ここでは簡単のために、係数を省略していたり、バストが本当に垂れてしまうような状況は考えていなかったりするので、ごく簡易的なバスト曲線方程式だと思って欲しい。大雑把に係数などを無視して、言葉で言ってしまえば、バスト曲線の傾きの変化はその点より上に位置するバストの重量に等しい、という感じである。自由境界におけるLaplaceの関係でも連想して頂ければわかりやすいだろうか?とにかく、この条件と適当な境界条件さえ入れてやれば、「水風船バストモデル」におけるバスト曲線B(y)は計算することができるのである。
さて、このバスト曲線方程式を一般化したり、係数をちゃんと計算したり、三次元に拡張したりということはまたいつか行うことにして、まずは適当にこのバスト曲線方程式を数値的に解いてみた。それが、例えば、次の図である。これが、「水風船バストモデル」のバストの形状の一例だ。
赤:すごくハリのあるヤングな皮膚の場合 |
この図の中でバスト形状のプロットが三種類あるのは「皮膚のハリ = 皮膚のヤング率」として三種類の値を使ってみたからだ。以前
の中でそう、もうお判りのはずだ。 「バストに関するヤング率」はまさにヤング率(Young率)なのである。実は年齢に比例する係数だったのだと書いたが、あれと同じである。今回は、年齢で変わっていくバストの皮膚のハリを「バストの皮膚のヤング率」とおいてみたのである。そういうわけで、皮膚のハリ= 皮膚のヤング率によってバストの形状は異なるわけだが、まずは眺めてみてもらいたい。以前のどうみても不自然な「半球バストモデル」等に較べて、ずっとましになっているとは思わないだろうか?特に、藍色・マゼンダのプロットなどかなり自然な形状になっていると思うのである。感受性の豊かなオッパイ星人であれば、必ずしやググッとくるハズである。
さすがに、メチャクチャ皮膚のハリがある赤色のプロットなどは松坂大輔もビックリの「超ロケット乳」になってしまっているが(といっても、この図のアスペクト比に意味はないんだけど)、今や時代は二十一世紀、宇宙へロケットで飛び出す時代だと思えば、こんな「超ロケット乳」を眺めるのもそれまた一興ではないだろうか。ぜひこの「超ロケット乳」には宇宙へ飛び出してもらいたいものである。
もちろん、世の中には「大きいことは良いことだ」という巨乳大好きオッパイ星人達もいるわけで、そんな人達のためにもう少し「大きいバスト」の場合で計算してみたものと並べて比較してみたのが次の図である。
 |
個人の好みもあると思うが、けっこう自然な「巨乳形状」が再現できている。ちなみに、今回使用した簡易的なバスト曲線方程式ではすごく巨乳だったり、皮膚のハリが無さ過ぎてあまりにバストが垂れている場合の計算はできない。簡単に言えば、Yに対してバスト曲線B(Y)が一対一対応しないためである。が、それゆえに巨乳と言っても美乳の範囲のみ考えることができるのである。
また、この「小さいバスト」の場合と「大きいバスト」の場合の比較から、「巨乳は垂れるのよっ!だから、小さい方が良いのっ!」という世の小振りなバストの女性がよく言うセリフの妥当性も確認してみたいところではなるが、そういうことは何か危険なことであるような気もしてきたので、今回は止めておきたい。
ところで、今回の話はAnti-Gravityから話が始まっているわけだが、ちなみに「水風船バストモデル」は無重力下ではどのような形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。つまり、「半球バストモデル」は「水風船バストモデル」の重力を無視した特殊な場合であり、逆に言えば「水風船バストモデル」は「半球バストモデル」にバスト内部での重力の影響を加えて一般化したものだったのである。
今回は、とりあえず新たに「水風船バストモデル」を提唱し、そのモデルにおけるバスト曲線B(y)を解くための簡易的な方程式を考察し、それを数値的に試しに解いてみた。次回は今回行った考察を用いながら、少し違うアプローチで「オッパイ星人の力学」を考えてみたいと思う。
さて、今回の話のきっかけともなった黒谷氏らの書いた本「星と生き物たちの宇宙」は原稿のごく初期の段階で実は読ませてもらっていた。その時感想を聞かれたときは、この本はメールのやりとりで構成されているので、「なるべく著者達の私的な部分を消さないままにしておいた方が面白いんじゃないか」なんて適当なことを言っていたのだった。その著者達が書いたこの本のあとがきの言葉を最後に引用して、これからの「オッパイ星人の科学」への「戒め」と「言い訳」としておきたい、と思うのだった…
科学は応用を通じて実生活に関わり、知的追求というこころの喜びにも関わる二面を持っています...多くの人に、こころを喜ばせる科学を楽しんでもらいたいですね。 H.Hirax, A.Kurotani
2002-12-12[n年前へ]
■黒谷"和泉" 明美さん@ネットサイエンス・インタビュー・メール 
今朝届いてたネットサイエンス・インタビュー・メールを夜になってから眺める、と何処かで見たようなお名前。いや、見たような所ではなくて、hirax.netにアカウントがある黒谷"和泉" 明美さん@宇宙科学研究所、である。 というわけで、そのメール中に書かれていた『絵でわかる細胞の世界』のネット上での原画展のURLを見てビックリするのだった。