1999-10-31[n年前へ]
■ビックエッグの力学 
ドームを支える空気圧の謎
この回は(トンデモ話)であり、中途半端であるのだが、反省を込めてこのままにしておく。直すのが、面倒くさいわけではないので、念の為。
日本シリーズ'99をやっている(いた)。私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。そういえば、今年はドーム決戦である(だった)。ドームといえば元祖「東京ドーム」だろう。「東京ドーム」のWEB
- 株式会社東京ドーム (http://www.tokyo-dome.co.jp/about/index.htm )
| 東京ドームは、空気膜構造によるエアドーム。つまり内部気圧を外気より0.3％高くして、400トンもの超特大楕円形の屋根を膨らませるのがドーム建築のポイントなんだ。 ところで、この気圧差0.3％は、ビルの1Fと9Fぐらいの違いがある。とはいえ中と外の違いを体感することはほとんどない。 |
たった、0.3%の空気圧の差で400トンを支えるとは、ものスゴイ。すぐには納得できない数字である。別に疑い深い私でなくても不思議に思うことだろう。
そこで、確かめてみることにした。まずは、東京ドームの面積をx(m) * x(m)としてみる。すると、持ち上げることのできる重さ(トン)は、
- 0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x / 1000(kgからトンへ)* 9.8(Nから重力へ)
と計算できる(この式には実は間違いがある。詳細は後で...)。その結果を示してみる。
 |
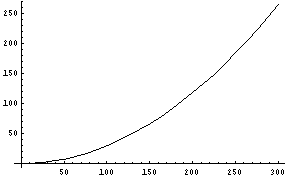先の、Webから東京ドームのサイズを見てみると、x = 180mである。すると、持ち上げられる天井の重さは100トン程度であるということになる。おやおや、先の「400トンの天井を持ち上げる」というのとはずいぶん違う。これでは、天井を支えきれない。
 |
そこで、高さによる大気圧の差を導入し、天井近くの高い場所では「外部の気圧が低い」という条件を導入してみる。0.3%というのは地上での比で、天井のある上空ではさらに差があるとしてみるのだ。うーん、強引である。
さて、ここから後は(実は前も)トンデモ話になっているので眉に唾をつけて読んで欲しい。それを指摘して下さった、読者からの手紙への返事(とほぼ同じ内容)を下に示しておく。
青木さんへの手紙> 高さによる圧力の差は、高さの異なる二点間に存在する空気> の重さに見合ったものです。したがって、ドームの内部でも> 高いところほど圧力は低くなっている筈です。 その通りだと思います。WEB中で「うーん、強引である。」と書いたのはまさにその理由です。 それにも関わらず、強引な論法を続けたのは、文章の最後に「謎は解けないのに、東京ドームは存在している。 少し、くやしい。 」と書いた理由と同じです。まるで、「宇宙人が水道橋の駅前駐車場にUFOを停めて、サラ金に入って行くのを目の当たりにしている」ような、気持ちなのです。くやしいと強引になるのです。あぁ、何て人間らしいのでしょうか... また、計算をしていた時に少し勘違いをしていました>もし、ドームの内外の温度が等しければ、地上でも天井でも内外の差圧は>同じになるはずです。と仰るとおり、差圧は等しいわけですが、それを0mにおける大気圧に対するパーセンテージに直すと、高度が高くなればなるほど、そこの気圧に対してはパーセンテージは高くなります。計算をしていた時にその「パーセンテージが高くなる」ことを「差圧が高くなる」ことと同じに扱うという間違いを犯してしまいました。もちろん、基準の気圧が小さくなっているので、パーセンテージが高くなっても本当は差圧は変わらないわけです。「考えることを手抜きしていた」と言ってもよいかもしれません。要反省です。>ドーム内の温度が高ければ空気の密度> が減少し、天井の位置での差圧はより大きくなり、天井を支> えるのに有利に働きます。これは、浮力によって天井が持ち> 上げられていると考えても同じ事です。> という訳で、ドーム内外の温度差が逆転する夏と冬とでは天> 井を支えるのに必要な圧力を変えなければならないと思うの> ですが本当はどうなんでしょうか。 これは面白そうですね。そういえば、学生時代に地殻物理学を専攻していたのですが、夏と冬の大気圧の違いから、地殻歪の大きさに関係づけて、地震の予言をするなら、「冬に発生する」といった方が良い、話(もちろんかなり冗談で)をしていた先生がいました。その先生に「今回のトンデモ話」がばれたら、大目玉をくらうこと間違いなしです。 ビックエッグの謎は深まるばかりです。それでは、また。------------------------------------------------------------------ch3coohさんへの手紙> > >12/(100*100)*1000= 1.2g/cm2となります。> > >> > >地上での大気圧は約1Kg/cm2なので、上の値は> > >1.2%程度となり、 ここが疑問だったのですが、これは1.2%でなくて、0.12%ですね。なるほど、0.3%よりも小さいですね。実に納得です。 さて、他の方からの指摘もあり、私の計算には> ＞0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x > / 1000(kgからトンへ) * 9.8(Nから重力へ)> に１０１３（標準気圧 hPa）がかかっていないことが気になりました。 という間違いがあることがわかりました。全てはここが原因だったようです。 全ての疑問が解決しました。いやぁ、お恥ずかしい。また、他にも色々と面白い情報ありがとうございます。
ひとつわかったことは、間違いをすると読者からの手紙が沢山来るといううれしくもつらい事実であった。ここから、あとは封印したい思いで一杯なのだが、自戒を込めてこのままにしておく。しつこいようだが、直すのが面倒なのではない。
それでは、高さによる大気圧の差を計算してみる。理科年表から15℃の「標準大気の場合の高さと気圧の表」を見てみる。 ちなみに、東京ドームの温度は、「ガス熱源による冷暖房システムにより、夏期は28℃の冷房、冬期には18℃程度の暖房が行われている」とある。今回の計算は外気の温度が15℃で、内部は冬期には18℃程度の温度に調整されているものとしておこう。
標準気圧は海抜0mで1013mbであり、200mでは989.5mbである。理科年表が古いのでPascal値でなく、mb表示になっている。
これから、1m当たりのmb変化を計算すると、0.12mb/mとなる。比率に直すと、0.012%/mということになる。例えば、「ビルの1Fと9Fぐらい」の高さの差は30m位であろうから、それを大気圧の比に直すと、99.6%位となり、先の記述と大体合う。
以下に、高度に対する大気圧の差(の比 %)を示してみる。
 |
このグラフで30mの場所を見てみると、99.6%位というわけだ。これが、先のWEB上の「この気圧差0.3％は、ビルの1Fと9Fぐらいの違いがある。」という説明と合うわけである。
次に必要なのはドーム外部と内部の大気圧の比から、力に直してみる。基準面からの高さ0mにおける気圧を1hPaとして、1hPa = 10^2 N/m^2 = 10^2 m^-1 kg s^-2という単位換算を使うと、持ち上げることのできる重さは、
- (100-大気圧の差(の比 % )) / 100(%から単なる比へ) *9.8(重力に換算) / 1000(kgからトンへ)* 100(hPaからN/m^2へ) * x^2(ドームの面積)
東京ドームの高さは「グラウンド面から 61.69m」とあるので大雑把に100mとしてみる。
 |
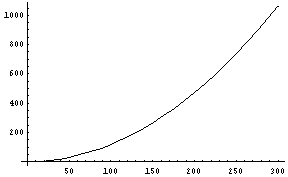この計算結果によれば、東京ドームのサイズを180mとした時には、「持ち上げることのできる力」は400トン位になっている。ということは、先のWEBの記事と大体一致するわけである。
しかし、この計算では致命的な欠陥がある。天井の高度が低いときには、400トンを持ち上げるためにはもっと高い「ドーム内部の圧力を必要とする」ことだ。
例えば、0.3%空気圧の差の条件で、「天井の高度」に対する「持ち上げることのできる力」を計算してみると、次のようになる。
 |
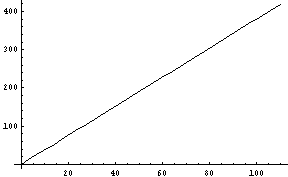これでは、天井の高さが下がるとますます天井の重さを支えきれなくなってしまう。それに、そもそも天井をどうやって持ち上げたのだ?屋根を持ち上げるインフレートという作業はどうやって行ったのだろう?
今回の計算は謎が増えただけかもしれない。謎は解けないのに、東京ドームは存在している。
少し、くやしい。
2002-02-11[n年前へ]
■めがねっこ大好き。
めがねを外すと美人になるは本当か!?
理系＝めがねっこ大好き？ 「どんな時に自分を理系だと思う？」と文系人間に聞かれた。私は「うむむ…」と答えに詰まってしまった。そんな私に、その文系人間はまるで勝ち誇ったような表情で「じゃぁ、理系と文系はどう違うと思う？」と畳みかけるように聞いてきた。この手の数限りなくある、「理系と文系」「男と女」はどう違う？という問いには立ち入ってはいけない、というのが私の家の代々の家訓なのであるが、ここで黙りこんでいては「勝ち負け」でいうところの「負け」だと思ったのか、理系の誇りを守るべく、私の口がいきなりしゃべり出した。
例えば、建築で言えば、鉄骨建築が理系で、プレハブ住宅が文系なのである。体で言えば、皮膚の感覚を大事にするのが文系で、骨から組み立てていくのが理系なのである。つまり理系は骨があるのである。そして、詩で言えば、散文詩は文系で定型詩が理系なのである。つまり、理系は型にこだわる部分があるのである。と、スキーのモーグル競技でコントロールを失い、コースアウトしてしまう選手のように私の口は暴走を続け、理系＝めがねっこ大好き、という辺りではもう「勝ち負け」でいうところの「負け犬」であるようにしか思われず、理系の誇りを守るどころか、理系を単に汚しただけに終わってしまった。そこで、悔しさのあまり、今回は「めがねっこ」に対し理系的なアプローチで近づいてみることにした。そして、私が汚してしまった理系の汚名をすすぎたいと思うのである。だから、例えば理系は女子高生の制服が大好きなのである。色々ある女子高生をセーラー服（あるいはブレザー）という記号で記号・集合論的に取り扱うことを可能にし、その記号を言葉にし、ついにはその制服を見るだけで萌えることができるのである。それが理系なのである。
つまりは、「このアイドルがなんとなく好き」というのが曖昧模糊としたものが文系であるならば、「このアイドルがめがねっこだから好き」という確固とした意志それすなわち理系なのである。理系＝めがねっこ大好きなのである。
「めがねを外すと美人になる」は本当か!?
よく、少女マンガなどで、「ヒロインが眼鏡をとると美人になった」というストーリーをみかける。今はどうだか知らないが、少なくとも昔はよくそんなストーリーを見かけた。あれは果たして本当だろうか。そして、それが本当であるならばそれは一体どんな物理現象なのだろうか？そして、ヒロインが眼鏡をとると美人になった」というストーリーと「めがねっこ大好き」というそ相反する二つの事象はどんな原因に基づいているのであろうか？それを理系的なアプローチで明らかにしてみたいと思う。
めがねはもちろん視力が悪い場合に、その矯正を行うための道具である。近視の人であれば矯正のために凹レンズをかけるし、逆に遠視の人は矯正のためには凸レンズをかける。凸レンズと言えば、虫眼鏡と同じで、何かの近くにレンズを持っていけばそれが拡大されて見える。また、逆に凹レンズであれば、対象物が小さく見える。
 |
だから、近視の人が凹レンズである眼鏡をかけた場合には、その人の目が他の人からは小さく見えてしまうのである。実世界でも、少女マンガの世界でも大きな瞳は美少女の象徴であるが、近視の人が眼鏡をかけると、大きな瞳を持つ美少女でもちっこい瞳になってしまうのである。
試しに、仲間由紀恵に凹レンズの眼鏡をかけさせた場合の、シミュレーションを行ってみたのが下の結果である。左のめがねをかけた「近視の」仲間由紀恵は確かにキレイではあるけれど、右の仲間由紀恵の方が、美少女という魔性の魅力という点で遙かに勝っていることが判るだろう。
 |  |
そう、近視の人の場合には、「めがねを外すと美人になる」は物理的に本当なのである。近視の人の割合は国によって大きく違うらしいが、少なくとも現代の日本では近視の人の割合は圧倒的に多い。ほとんどの人が近視である、といっても良いくらいである。ということは、そんな日本では「めがねを外すと美人になる」はかなりな確率で事実である、と言えるわけだ。
それでは、「めがねを外すと美人になる」ということと相反するとしか思えない「めがねっこ大好き」現象をどう説明したら良いだろうか？一つは、遠視の場合先の近視の場合と逆のことが起きる、ということである。すなわち、遠視の人の場合には、眼鏡をかけると瞳が大きく見えるのである。すなわち、眼鏡をかければ、美少女の象徴たる大きな瞳が手に入るのである。
下の「遠視の」仲間由紀恵の場合の眼鏡シミュレーションを見てみると、めがねをかけたことでずいぶんと美少女度がアップしていることが判ることと思う。まさに、その瞳には魔性の魅力が宿っているとしか思えないほどなのである。
 |  |
ということは、「眼鏡を外すと美人になる」は本当。ただし、近視の人の場合は、ということなのだ。そして、もし遠視の人であれば、「眼鏡をかけると美人になる」が本当なのである。
とはいえ、日本人では遠視の人は少ないわけで、それではめがねっこを増やす原因たる「眼鏡をかけると美人になる」が少なくなってしまう。そこで、他の原因を考えてみると、例えば近視の人が裸眼の時には瞳の口径を小さくすることで、被写界深度を深くする、すなわちハッキリとものを見ようとして、目を細めがちであること、すなわち小さな瞳になりがちであること、なども原因の一つとして考えられるだろう。
そしてまた、実は近視の程度が低い場合には、「めがねっこ大好き」現象を支えるもう一つの事実がある。レンズの度数がきつくなくて、他の人から見た瞳の拡大縮小が行われないような場合にも、眼鏡をかけると実は心理的に瞳の大きさが変わって見えるのである。
下の「目が小さい」仲間由紀恵は左右で目の物理的な大きさは完全に同じである。が、心理的には結構違って見える。眼鏡をかけた仲間由紀恵の方が目が大きく見えることが判ると思う。「目が小さい」場合、めがねをかけると瞳が大きく見えるのである。
「目が小さい」仲間由紀恵 | 「目が小さい」仲間由紀恵 |
日本人は目が小さい人が多いから、このような眼鏡をかけると心理的に瞳が大きく見える影響は無視できないに違いない。
ところが、目がもともと大きい場合には、この現象はそれほど大きく現れるわけではない。もともと瞳が大きいがために、眼鏡をかけたからといって割合的にそれほど瞳が大きく強調されたりはしないのである。その例を下に示す。下の二枚は目の物理的な大きさは完全に同じなのであるが、心理的に受ける瞳の大きさ＝美少女度の違いは上の例ほどではないことが判るだろう。
「目が大きい」仲間由紀恵 | 「目が大きい」仲間由紀恵 |
ということで、
- 瞳が多きい近視の人の場合、眼鏡を外すと美少女になる
- 目が小さかったり、遠視だったりする人の場合、「めがねっこ」＝美少女になれる
ところで、理系と文系…
さて、理系的「めがねっこ大好き論」も良いのだが、話をそもそもの「どんな時に自分を理系だと思う？」という問いに戻ろう。
よく私が見かけるパズルは大抵が論理的なパズルだ。論理的＝理系ではないから、それを理系パズルと呼ぶのはいけないと思うが、あえてそれを理系パズルと呼んでみる。間違っているのを承知で、あえてここではそう呼んでみる。
そんな理系のパズルでもやっぱり色々あるだろう。大抵のそんなパズルの答えは答えがただ一つに限られるものだろうが、時にはその答えが無限にあるものもあるかもしれない、そして答えが一個もないパズルだってあるかもしれない。そしてまた、「答えを見つけられないこと」を証明できるようなパズルだってあるだろう。だけど、いずれにせよ、そのパズルを解く過程で現れようとする「割り切れない何か」は「それが割り切れる軸」を駆使することで、巧妙に消し去っていくことができる。だから、とてもそれは結構気持ちが良い作業だ。少なくとも、私にはそうだ。あるいは、答を判定するものが、自分ではない論理なり自然現象に任せられているから楽なのかもしれない。
だけど、もしそんな論理的なパズルとは違う非論理的なパズル、ここではあえて文系のパズルと呼ぶようなものがあったとしたら、その答えは「割り切れない何かを拾い集めたようなもの」であるような気もする。そして、その解く過程はもしかしたら割り切れない感情や雰囲気を拾い集めて、割り切れないままに何とか答えを投げ出しいく作業であったりするのかもしれない。それに、そこでは答を判定する何かなんかそもそも存在しないか、あるいはその判定する何かが人であるのかもしれない。
私には、そんな「割り切れないままに何とか答えを出していく作業」はちょっと辛いなぁと思う。やっぱり、私は理系パズルの方がずっと楽で気持ちが良い。だから、今度「どんな時に自分を理系だと思う？」と聞かれたら、そんなことを上手く言えたらいいな、と思う。いつも、思い浮かべたことを伝え続けたいな、と思う。
2003-01-12[n年前へ]
■組み上げ絵
「ペーパークラフト」で書き加えられていた「建築ペーパークラフト」も確かに面白いなぁ、と思っていた。そしたら、今日偶然日本浮世絵博物館で昔々に作られた「凌雲閣」の紙模型を見た。ちなみに別の新聞記事ではこんな感じになっている。こんなペーパークラフト、「紙」で作るいろんなもの・昔のもの・世界のもの、ちょっとそんな風に眺め直してみようかな。
そういえば、シザーハンズは大学時代に見ました。少しホロリときました。
2004-01-21[n年前へ]
■Origamic Architecture and Escher
エッシャーの世界を折りたたみカードで。立体に飛び出す折り紙・切り紙が表現するエッシャーの世界。まさに折り紙の建築。
こんなカードは是非欲しいもの。
2004-07-12[n年前へ]
■'79.10.26-
ザテレビジョン別冊３年Ｂ組金八先生25周年メモリアル。生徒達、PTAを前に四人の教師が「愛とは何か」について延々と語る授業や、色んなことを語る長台詞を懐かしく、そして強く思い出したければ、買ってみるといい。現在、２級建築士・一級建築施工管理技師の資格を持つ直江喜一所長、つまりは"腐ったミカン(じゃない)"加藤優のインタビューも載っている。
こんな話は古いかもしれない。けれど、それはとても当たり前、だって、「25周年メモリアル」なんだから。もう、ずっと昔の話なんだから。
12年経つと21世紀がやってきます。世界はより支え合わなければ生きていけない時代であります。第3シリーズ('88.10-'88.12) 12話
」など。
