1999-10-31[n年前へ]
■ビックエッグの力学 
ドームを支える空気圧の謎
この回は(トンデモ話)であり、中途半端であるのだが、反省を込めてこのままにしておく。直すのが、面倒くさいわけではないので、念の為。
日本シリーズ'99をやっている(いた)。私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。そういえば、今年はドーム決戦である(だった)。ドームといえば元祖「東京ドーム」だろう。「東京ドーム」のWEB
- 株式会社東京ドーム (http://www.tokyo-dome.co.jp/about/index.htm )
| 東京ドームは、空気膜構造によるエアドーム。つまり内部気圧を外気より0.3%高くして、400トンもの超特大楕円形の屋根を膨らませるのがドーム建築のポイントなんだ。 ところで、この気圧差0.3%は、ビルの1Fと9Fぐらいの違いがある。とはいえ中と外の違いを体感することはほとんどない。 |
たった、0.3%の空気圧の差で400トンを支えるとは、ものスゴイ。すぐには納得できない数字である。別に疑い深い私でなくても不思議に思うことだろう。
そこで、確かめてみることにした。まずは、東京ドームの面積をx(m) * x(m)としてみる。すると、持ち上げることのできる重さ(トン)は、
- 0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x / 1000(kgからトンへ)* 9.8(Nから重力へ)
と計算できる(この式には実は間違いがある。詳細は後で...)。その結果を示してみる。
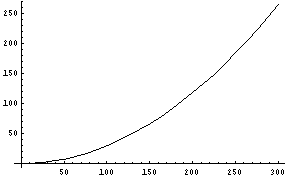 |
先の、Webから東京ドームのサイズを見てみると、x = 180mである。すると、持ち上げられる天井の重さは100トン程度であるということになる。おやおや、先の「400トンの天井を持ち上げる」というのとはずいぶん違う。これでは、天井を支えきれない。
 |
そこで、高さによる大気圧の差を導入し、天井近くの高い場所では「外部の気圧が低い」という条件を導入してみる。0.3%というのは地上での比で、天井のある上空ではさらに差があるとしてみるのだ。うーん、強引である。
さて、ここから後は(実は前も)トンデモ話になっているので眉に唾をつけて読んで欲しい。それを指摘して下さった、読者からの手紙への返事(とほぼ同じ内容)を下に示しておく。
青木さんへの手紙> 高さによる圧力の差は、高さの異なる二点間に存在する空気> の重さに見合ったものです。したがって、ドームの内部でも> 高いところほど圧力は低くなっている筈です。 その通りだと思います。WEB中で「うーん、強引である。」と書いたのはまさにその理由です。 それにも関わらず、強引な論法を続けたのは、文章の最後に「謎は解けないのに、東京ドームは存在している。 少し、くやしい。 」と書いた理由と同じです。まるで、「宇宙人が水道橋の駅前駐車場にUFOを停めて、サラ金に入って行くのを目の当たりにしている」ような、気持ちなのです。くやしいと強引になるのです。あぁ、何て人間らしいのでしょうか... また、計算をしていた時に少し勘違いをしていました>もし、ドームの内外の温度が等しければ、地上でも天井でも内外の差圧は>同じになるはずです。と仰るとおり、差圧は等しいわけですが、それを0mにおける大気圧に対するパーセンテージに直すと、高度が高くなればなるほど、そこの気圧に対してはパーセンテージは高くなります。計算をしていた時にその「パーセンテージが高くなる」ことを「差圧が高くなる」ことと同じに扱うという間違いを犯してしまいました。もちろん、基準の気圧が小さくなっているので、パーセンテージが高くなっても本当は差圧は変わらないわけです。「考えることを手抜きしていた」と言ってもよいかもしれません。要反省です。>ドーム内の温度が高ければ空気の密度> が減少し、天井の位置での差圧はより大きくなり、天井を支> えるのに有利に働きます。これは、浮力によって天井が持ち> 上げられていると考えても同じ事です。> という訳で、ドーム内外の温度差が逆転する夏と冬とでは天> 井を支えるのに必要な圧力を変えなければならないと思うの> ですが本当はどうなんでしょうか。 これは面白そうですね。そういえば、学生時代に地殻物理学を専攻していたのですが、夏と冬の大気圧の違いから、地殻歪の大きさに関係づけて、地震の予言をするなら、「冬に発生する」といった方が良い、話(もちろんかなり冗談で)をしていた先生がいました。その先生に「今回のトンデモ話」がばれたら、大目玉をくらうこと間違いなしです。 ビックエッグの謎は深まるばかりです。それでは、また。------------------------------------------------------------------ch3coohさんへの手紙> > >12/(100*100)*1000= 1.2g/cm2となります。> > >> > >地上での大気圧は約1Kg/cm2なので、上の値は> > >1.2%程度となり、 ここが疑問だったのですが、これは1.2%でなくて、0.12%ですね。なるほど、0.3%よりも小さいですね。実に納得です。 さて、他の方からの指摘もあり、私の計算には> >0.3 / 100(%から比へ) * 100(hPaからN/m^2へ) * x * x > / 1000(kgからトンへ) * 9.8(Nから重力へ)> に1013(標準気圧 hPa)がかかっていないことが気になりました。 という間違いがあることがわかりました。全てはここが原因だったようです。 全ての疑問が解決しました。いやぁ、お恥ずかしい。また、他にも色々と面白い情報ありがとうございます。
ひとつわかったことは、間違いをすると読者からの手紙が沢山来るといううれしくもつらい事実であった。ここから、あとは封印したい思いで一杯なのだが、自戒を込めてこのままにしておく。しつこいようだが、直すのが面倒なのではない。
それでは、高さによる大気圧の差を計算してみる。理科年表から15℃の「標準大気の場合の高さと気圧の表」を見てみる。 ちなみに、東京ドームの温度は、「ガス熱源による冷暖房システムにより、夏期は28℃の冷房、冬期には18℃程度の暖房が行われている」とある。今回の計算は外気の温度が15℃で、内部は冬期には18℃程度の温度に調整されているものとしておこう。
標準気圧は海抜0mで1013mbであり、200mでは989.5mbである。理科年表が古いのでPascal値でなく、mb表示になっている。
これから、1m当たりのmb変化を計算すると、0.12mb/mとなる。比率に直すと、0.012%/mということになる。例えば、「ビルの1Fと9Fぐらい」の高さの差は30m位であろうから、それを大気圧の比に直すと、99.6%位となり、先の記述と大体合う。
以下に、高度に対する大気圧の差(の比 %)を示してみる。
 |
このグラフで30mの場所を見てみると、99.6%位というわけだ。これが、先のWEB上の「この気圧差0.3%は、ビルの1Fと9Fぐらいの違いがある。」という説明と合うわけである。
次に必要なのはドーム外部と内部の大気圧の比から、力に直してみる。基準面からの高さ0mにおける気圧を1hPaとして、1hPa = 10^2 N/m^2 = 10^2 m^-1 kg s^-2という単位換算を使うと、持ち上げることのできる重さは、
- (100-大気圧の差(の比 % )) / 100(%から単なる比へ) *9.8(重力に換算) / 1000(kgからトンへ)* 100(hPaからN/m^2へ) * x^2(ドームの面積)
東京ドームの高さは「グラウンド面から 61.69m」とあるので大雑把に100mとしてみる。
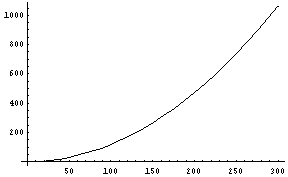 |
この計算結果によれば、東京ドームのサイズを180mとした時には、「持ち上げることのできる力」は400トン位になっている。ということは、先のWEBの記事と大体一致するわけである。
しかし、この計算では致命的な欠陥がある。天井の高度が低いときには、400トンを持ち上げるためにはもっと高い「ドーム内部の圧力を必要とする」ことだ。
例えば、0.3%空気圧の差の条件で、「天井の高度」に対する「持ち上げることのできる力」を計算してみると、次のようになる。
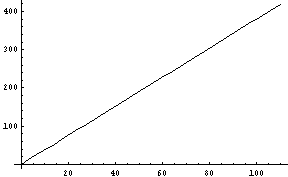 |
これでは、天井の高さが下がるとますます天井の重さを支えきれなくなってしまう。それに、そもそも天井をどうやって持ち上げたのだ?屋根を持ち上げるインフレートという作業はどうやって行ったのだろう?
今回の計算は謎が増えただけかもしれない。謎は解けないのに、東京ドームは存在している。
少し、くやしい。
2000-06-11[n年前へ]
2000-11-26[n年前へ]
■ブランコの中の∞(無限大) 
なんで一体漕げるのだろう?
公園のブランコというのは、何故かとても不思議な雰囲気を持っている。ホントにうるさいくてたまらないくらいのガキんちょ達が、アクロバットのようなスゴイ技を見せていたりする。それは、まるで上海雑伎団を見ているような気分になる。小さな子がなかなかブランコが漕げず、ブランコの上で宇宙遊泳のように四苦八苦しているのを見ているのも思わず笑ってしまうくらいに可愛らしいものだ。もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。
やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう?口で上手く説明できる人がいるだろうか?
それに、そもそも私たちはブランコを何故漕ぐことができているのだろう?
いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?という手紙で始まるのは加納朋子の「ななつのこ」だが、「何故、リンゴは落ちるのかという謎」と同じく、「ブランコの漕ぎ方の謎」だってとても不思議だ。いつも目にする公園のブランコを、私たちは一体どうやって漕ぐことができているのだろう?
いつだって、どこでだって、謎はすぐ近くにあったのです。
何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。
もちろん、「何でブランコの漕ぎ方が不思議なのさ?」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。
次の図は「ブランコを漕いでる子供」である。
 |
この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか?それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。
だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか?
次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、
- ブランコの動きの中心を向いている軸A
- 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B
 |
ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。
それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。
というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。
ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか? この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか?
 |
「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ!)上がれば、ブランコの速度はもとの速度の倍になるのである!
ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。
もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ!
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。
このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、
- 初期のブランコの速度 = 10
- 重心位置を高くして 10 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- 重心位置を低くして 10 X 1/2 = 10 (何てこったい、速度が半分になっちまったか!)
- 初期のブランコの速度 = 10
- 重心位置を高くして 0 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- そのあとブランコの速度 = 0
- 重心位置を低くして 0 X 1/2 = 0 (0が0になっても全然変わってないもんね!ヘヘン!)
人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。
まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。1万円×2=二万円では1万円しかもうからないが、一千万円×2=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。
もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。
そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね!となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。
というわけで、
- ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
- ブランコが上に行ったときにその姿勢を元に戻す
それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。
というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ
- 何もしない場合
- ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
- ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合
 → ブランコの動きはず〜と変わらない |
ブランコが上にきたあたりで座り込んだ場合  → ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」 |
ブランコが上にきたあたりで立ち上がった場合  → ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」 |
この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。
ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか? それとも、ちょっと考え過ぎかな。
2002-04-13[n年前へ]
■月が遠くであっち向いてホイ 
Stereographs of the Lunar Libration
夜、月をよく眺める。仕事の帰り際に箱根山中で、あるいは信号待ちをしてる車の中から、よく月を眺める。そんな時、こんなことを考えた。
月の自転周期と、月が地球の周りを回る公転周期は同じだ。月の潮汐力が原因で、どうしても自然に一致してしまう。少しでもそのその二つがずれた場合には、それを元通りにするような力が働く。だから、月はいつでもほとんど同じような顔を地球に向けている。もちろん、太陽の方向に従って月の満ち欠けはあるのだけれど、それでもやはり顔はいつも同じ面を向けている。それはまるで「心配そうに子供を見守る親」か、「ワガママな姫さまを心配する爺や」か、はたまた「好きな人を飽きもせず眺めてる恋する人」であるかのようだ。
とはいっても、月の軌道は実際には楕円だから、本当はこんな風に秤動を起こす。地球に近づいたり遠ざかったり、早く動いたり遅く動いたりして、月は少しづつ違う顔を地球に見せる。それでも、それは「子供を何故か怒ってしまったり、可愛がったりする親」か、「爺やが心配そうに姫さまに顔を向ける仕草」か、「誰か好きな人を少し不器用に見てる恋する仕草」のようで、やはりなんとなく微笑ましい。
ところで、そんな風に月が少しだけ違う顔を見せるのなら、そんな月の写真を二つ並べて眺めてみれば、目の前に立体的な月の姿が浮き上がってくるはずである。同じ時の、だけど空間的に少しだけずれた場所から眺めた二枚の画像が立体感を与えるのは当たり前の話だけれど、時間的に少しだけずれた(だから空間的にも少しだけずれた)二枚の写真にだって、私たちはやっぱり立体感を感じる。
そこで、試しにインターネット上から月の写真を二つ拾い上げてみた。下の写真は誰かが何処かで眺めた二つの月だ。撮影された場所も、時間も(きっと)全く別の二つの月である。平行法だったら遙か遠くの誰かを眺める要領で、交差法だったら目のすぐ前の誰かを眺める要領でこの二つの月を眺めてみれば、立体的な月を眺めることができる。GoogleImage Searchのおかげで、そんなこともずいぶん簡単になった。何時か何処かの誰かが月を眺めている目を通して、それを自分の目の代わりにして、自分の心の中に月の立体的な様子を映し出しているのだから、いわば私の左右の目が「インターネットの大きさ」だけ離れて、立体感を拡大しているような感じで、少し面白いような感覚がする。
 |  |
 |  |
ところで、こんな風に月が地球に向ける二つの顔を見るとき、私たちが立体的な月の姿が目の前に迫ってくるかのように感じるように、人の表情が顔の向きが少しだけ違う写真を用意して、そんな写真をぼーっと眺めてみたら、私たちの目の前に「その人の姿」が浮かび上がってくるような気持ちになる。
実際のところ、私たちが心の中で人を思い浮かべたりする時は、自分では気づかなくとも、色んな時や色んな場所での「その人の姿」を心の中に浮かべているのかもしれない。そして、もしかしたら「その人の立体的な姿」を心の中で感じているのかもしれない。きっと無意識にだけど、私たちはそんなことをしているのだろう。
だから、そんな心の中で無意識にしていることを、不器用だけど意識的にやってみれば、案外自分の「心の中の立体感」や、「心の中にいる誰かの立体像」なんかを上手く眺めることができるかもしれない。例えば、アルバムの中から二枚の写真を適当に選んでぼーっと眺めてみたりしたら、そんなものがもしかしたら心の中に浮かび上がってくるのかもしれないな、と月を眺めながら考えてみたりしたのである。
2003-02-23[n年前へ]
■ブラジャー・カップ解体新書 
オッパイ星人のJIS規格
ワタシは人知れずオッパイ星人と長い戦いを続けている。それはとても孤独な戦いではあるのだけれど、時にはワタシの正義の意志を理解し、ワタシと同じく地球を守ろうとする同士から貴重な助言をもらうこともある(たまに)。例えばそれは、「オッパイ星人達の母星はどうやら二重星らしい」という異星人に関する情報であったり、「はてなダイアリとあるポータルサイト」がオッパイ星人により作り出された疑いがあるという情報であったり、Bカップ好きは「好みとしては中途半端、そんなの微妙過ぎー」であるらしいという教訓や、動画解析の参考になるのではないでしょうか?という20MB弱のエロムービービデオ資料や、とにかく色々と参考になる助言を(たまに)頂く。
そんな助言の中でも特に興味深かった情報が、エージェントたまごさんが調査した「たまごのじっけん。(おブラ解体新書?)」というブラジャーのサイズに関する調査資料だ。たまごさんからの
一度、たった一度でいいので、(ブラジャーを)着用してみてください。そうすると、というアドバイスと共に紹介して頂いた「ブラジャーのカップのサイズはどのようになっているか」ということを調査した貴重な資料なのである。これが非常にワタシの戦いの参考になったのである。
「あー女のヒトって、たいへんなのね~」
「ココはもうちょっと…」
など、新たなコトに気づくはずです。世の中の男の人が、必ず一度ずつ着用すれば、
もっと色々な下着が生まれると思うんですけどね~
なにしろ、オッパイ星人と戦ってはいるのだけれど、実際のところオッパイを自らの胸に装備しているわけでもないワタシが「オッパイ星人の力学 -胸のヤング率編 - 」の戦いを始めた頃は、『胸のバスト直下の部分の胸囲= 「アンダーバスト」と、バスト部分の胸囲 = 「トップバスト」の差からブラジャーのカップサイズが決まる』ということすら知らなかったのである。そしてまた、ブラジャーのカップのサイズを知るために、ブラジャーのサイズを規定しているというJIS規格JISL4006 「ファンデーションのサイズ」を取り寄せて調べてみたりもしたのであるが、そこには単に『「アンダーバスト」と「トップバスト」の差からブラジャーのカップサイズが決まる』という程度の情報しか記載していなく、具体的なブラジャーのカップ形状について役に立つ情報がほとんど得られなかったのである。
 |
仕方がないので、「胸のヤング率編」ではバスト形状として適当に「半球モデル」なんていうものを導入してみたわけであるが、それが果たして正しいのか否かですらこれまでワタシは皆目検討がつかなかったのである。ブラジャーのカップがそんな単純な形状だったりするかどうかは非常に疑わしいものだとすら思っていたのである。そしてまた、後の戦いである「オッパイ星人の力学第四回 - バスト曲線方程式 編 -」では 「水風船モデル」なんていうものを提唱してみたが、この「水風船バストモデル」から計算されるすごくハリのあるヤングなロケットバストなんて想像上の産物に過ぎないとすら思っていたのである。こんな突き出た楕円体みたいなバストなんか果たして存在するものだろうか?と自分でも疑問に思っていたのである。
 |  赤:すごくハリのあるヤングな皮膚の場合 マゼンダ:普通のハリを持つ皮膚の場合 藍色:ちょっとハリの少ない皮膚の場合 |
しかし、「おブラ解体新書」の中にあるまどか(たまご)さんやリエンさんらによる
- 同一カップサイズ(A70, A75, A80, ...)では、アンダーバストが5cm増す毎に、カップ内側の直径が5mm増す。
- 同一アンダーバストサイズでは(A80, B80, C80, ...)では、カップサイズが1つ大きくなる毎にカップ内側の直径が5mm増す。
- つまり、アンダーバストが5cm小さくなり、カップサイズが1つ大きくなった場合には(ex.A80→B75)、カップ内側の直径は同じになる。
- 80cmAカップ
- 80cmEカップ
- 80cmIカップ
- 95cmAカップ,
- 115cmAカップ
そして、「おブラ解体新書」の中の重要な情報はそれだけでなく
- A70など、アンダーバストが小さくカップも小さい場合は、カップ深さがカップ半径に比較して小さい=扁平な楕円体バスト。
- A80とC70というような辺りでは、カップ深さとカップ半径が同じ=カップ内が半球
- D or Eカップ(アンダーバストサイズによりけり)以上の場合は、カップ深さがカップ半径に比較して大きい=ロケットバスト(突き出た楕円体バスト)
そして、こんな「おブラ解体新書」からの情報と
- ブラジャーのカップの容積や
- 75Gのブラのカップの深さが約10cm、90Dの深さが約8cmで、カップ底面の直径が75G、90D共に同じ15.5cm
今回挙げたのはワタシの戦いの毎日の一例に過ぎないが、ワタシのオッパイ星人との長い戦いを理解しワタシの戦いを助けてくれる同士からの情報を元に、ワタシはオッパイ星人と戦うための研究を日々続けているのである。それも全て、そんなワタシの正義の意志を理解してくれる人が(数少ないながらも)いるからなのである。
ところで、まどか(たまご)さんの「おブラ解体新書」のリンクページの「hiraxさん、かなりのおっぱい星人です」という一文はなんでしょね?ワタシは地球人でオッパイ星人じゃないっていうのに…?いや、ワタシの目の錯覚かな…?あと、
オッパイ星人なひらばやしさん、ってなんでしょね…。あのですね…、本当にワタシの正義の戦いを判ってくれてます…(涙)?オッパイ星人はワタシじゃないっっていうのに…。
眺めたり、撫でたり、はずしたり、かぶったりするだけでなく!
ぜひいちど、(ブラジャーを)着用してみてください