1999-02-28[n年前へ]
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
 |  |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
 |  |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 |  1階微分 |
 13/10 (=1.3)階微分 |  15/10 (=1.5)階微分 |  17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
1999-03-05[n年前へ]
■できるかな 
ドアの向こうには、
本サイトとドラえもんの共通点
以前、「iMacはドラえもんの夢を見るか?-さようなら、ドラえもん -(1999.02.03)」 の時にドラえもんの話を出した。今回もまたまたドラえもんの登場である。私はドラえもんをさほど読んでいたわけではない。しかし、ここまでドラえもんにこだわるのは、高校時代のサミー本田先生の教育の賜物なのかもしれない。今日(1999.03.05)の朝日新聞の朝刊に4面全面を使ってドラえもんの映画の広告が載せられていた。その内の1面を少し加工したものが下の写真である。
 |
「できるかな」がメインテーマの本サイトとしては、この「できたらいいな」というのは非常に興味を惹かれるコピーである。また、下に示す面の広告のコピーは「iMacはドラえもんの夢を見るか?-さようなら、ドラえもん -(1999.02.03)」 の時に最後に浮かんでしまった疑問の一つの答えであるようにも思う。
 |
「できたらいいな」という気持ちは、その答え故に起きるのであるし、だからこそ「できるかな」という考えが湧くのである。
ところで、本サイトの「できるかな」の名前の由来は「ノッポさんとゴン太くん」の「できるかな」、そして、西原理恵子の「できるかな」である。
- NHKの「できるかな」ビデオ情報 (http://www.nhk-sw.co.jp/kids/video/01838A1.html)
- 西原理恵子「できるかな」(http://www.fujisankei-g.co.jp/fusosha/senden/980124.html)
- 西原理恵子 「鳥頭の城」(公式サイト)(http://www.jah.ne.jp/%7Eaiai/riezo/index.htm)
おまけ
こういう広告を眺めていると、- ドラえもん
- パンドラの箱
- 量子力学
「クジラは哺乳類か魚類か?、論ぜよ。」
という題目であった。この題目についてレポート用紙5枚位で説明できるとお考えの方は不可確実である。言い換えれば、自分なりの「動物分類学を構築せよ」と言っているのである。その人の姿勢まで問われる深い問題である。
1999-12-12[n年前へ]
■色覚モドキソフトを作る(色弱と色空間その4) 
五十歩百歩
まず、先に書いておこう。今回は、
で作成したTrueColorと似たようなプログラムを作成してみたい。何しろ関係ない話が以降、長々と続くからである。昔から、科学者は「色」というキーワードに強く惹かれている、と思う。そんなことを私が思うまでもなく、量子色力学(quatumchromodynamics)、色つき空間群(Color-symmetry)等のキーワードにその事実は現れている。これらの言葉は普通に使われる「色」という言葉とは違う性質を表すものである。しかし、科学者が「色」というものを基本的なものであると感じているために、どんなものが対象でも、「性質」の代表的なものとして、「色」という言葉が連想されるのだろう。
私は学生時代の量子力学の授業のおかげで、「色」という言葉を聞くと今でも眠くなってしまうのである。何しろ、私の通う理学部の教室の横は農学部の畑だったのだ。教授の声と共に「モゥーーー」という牛の鳴き声が聞こえてくるのだ。教授の声と牛の鳴き声が絶妙のハーモニーとなるのである。ただでさえ眠くなるのに、そのハーモニーはクロロホルムもビックリの睡眠作用を発揮するのだ。私はそのハーモニーのおかげで何回も記憶を飛ばされた。
また、その牛達のおかげで、授業の中で「匂い」と聞いたりすると、牛の糞の「匂い」しか連想できないのである。困ったものである。あの農学部の畑がなければ、もしかしたら私は量子力学を好きになっていたかもしれない。そして、量子力学を極めていたかもしれないのだ...簡単に言えば私は量子力学の授業では落ちこぼれてしまったわけだ。
ところで、昔の科学者達を考えると、「色」に関わらなかった人を探すほうが逆に難しいように思う。ニュートン、マクスウェル、ヤング、ヘルムホルツなどが代表的である。当たり前である。物理・化学に関わらず、「光」には関わらざるを得ない。当たり前である。さまざまな計測を行ったり、エネルギーを考えたりする上で光は最も重要なモノである。
そして、「色」というものは「光」の大きな性質の一つである。しかも、それは「科学者自身にとっても」目に見える性質である。目に見えるものを無視する科学者は少ないと思われるので、科学者が「色」に関わらないわけにはいかないのだ。
割に最近の科学者でも、意外な分野の人が「色そのもの」の研究をしていることがある。例えば、シュレディンガーなども色空間の提唱をしていたらしい。確かに、量子力学から色空間へはつながりを感じないこともないのではあるが、少し意外でもある。そのシュレディンガーが提唱した色空間がどのようなものであるのか、私は残念ながら知らないのだが、波動を深く研究していたシュレディンガーが提唱する色空間というのは非常に興味のあるところである。また、化学。物理学者であるダルトンは自らも色弱であるため、特にその辺りのことを研究し、報告している。
さて、そのダルトンをinfoseekで検索してみると、
- ダルトンレンズ (http://www2u.biglobe.ne.jp/~ohsaka/index2.html )
もちろん、WEBページは会社の心(色弱と色空間 その2) - WEBページのカラーを考える 3 - (1999.08.10)で作成したTrueColorも同じような目的のために作成したものであるが、あれはあまりにも大雑把なモノだったので、作り直してみたいのである。なお、今回は画像のRGBとL、M、S錐体の反応の間の変換は
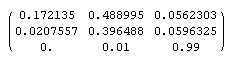 |  |
そこで、こういったWEB上の画像を読み込んで、
でやったL,M,Sの各錐体の感度が低いときの色覚シミュレーションを行うソフトを作成してみた。ソフトはこれである。前回と同じく、Susieプラグインを用いて画像を読み込んでいるので、「Susieの部屋」などから、Susie本体・あるいはプラグインを入手する必要がある。また、手間を惜しんだためProxy対応にはしていない。さて、動作画面サンプルを以下に示す。初期状態では
- ダルトンレンズ (http://www2u.biglobe.ne.jp/~ohsaka/index2.html )
 |
この画面例では各錐体の感度は全て100%になっている。
それでは、以下に適当に錐体の感度パラメータを変化させた場合のサンプルを示してみる。
 |  |
こうしてみると、これまで見てきたものとは違う数字が浮かび上がることがわかる。89,52などである。こういう仕組みを用いたのが、石原式などの色覚検査のやり方である。つまりは、異なる色を識別できないこと、すなわち、混同色を用いているのである。混同色を用いて文字を描くことにより、色弱であるかどうかを判断しようとするものだ。
さて、こういった書き方をすると、色を混同してしまうのが色弱の人だけと勘違いされてしまいそうであるが、そんなことはない。全ての人が「色を混同してしまう」のである。どんな人でも、異なる波長の光であっても、例えばRGBなどの(多くても)三色を混合すれば同じ色に見えてしまう。つまりは、混同色だらけなのである。健常者と呼ばれるヒトも色弱と呼ばれるヒトもたかだか数種類の錐体を持つにすぎない。
色々な光の波長分布を認識できる生物がいたとすると、彼らがからすればヒトは全て色弱ということになるのだろう。つまりは、五十歩百歩といったところなのかな、と思うのである。
2004-01-13[n年前へ]
■Everyone is..., until you put into hot water. 
少しばかり、先週聞いた言葉とオリジナルの言葉の違いが気に懸かっていたので、"Possibility"という言葉が好きだから量子力学を専攻したという彼女に、「先週の言葉をもう一度言ってみてくれません?」と今晩のレッスンの中で聞いてみる。すると、やはりこんなフレーズを言った。
"Everyone is like a tea bag,you don't know how strong you are until you put into hot water"この言葉だと、やはりオリジナル?の
"A woman is like a tea bag,you don't know how strong she is until you put her in hot water"
 という言葉とは大違いだ。この違いはとても大きい。
という言葉とは大違いだ。この違いはとても大きい。コーヒー豆を紙で濾過したコーヒーが美味しかったり、熱いお湯を紅茶の葉を紙で濾過した紅茶が美味しかったり、と何かを何かで濾過すると大きく姿を変えて良くなるものはたくさんある。それと同じく、誰かの頭の中で濾過された言葉が、オリジナルよりも素晴らしく響くことはよくある。これもそんな一つかもしれない。
2005-06-03[n年前へ]
■ロボットや白馬に乗った王子さま 
 Tech総研で「ロボット(人はそれを玩具と呼ぶ)や白馬に乗った王子さまのニュースなど」が公開されています。
Tech総研で「ロボット(人はそれを玩具と呼ぶ)や白馬に乗った王子さまのニュースなど」が公開されています。
野球盤の「消える魔球を実現するための苦労話」は有名です。「巨人の星」連載当時、「巨人の星」の消える魔球に関して「物理学的に解析すると…」という話がよくあったと聞きます(あるいは当時の書籍でそんな話を見かけます)。大リーグボール1号で「ラプラスの悪魔」を論じ、大リーグボール2号で「パラレル・ワールド」を論じ、(その頃未だ出現していなかった)大リーグボール3号は「量子力学」で説明することができるはず、という話が一番面白かったような…。