1999-10-18[n年前へ]
■沸点と数学の挑戦状 
みつからない「解決編」
| いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか? いつだって、どこでだって、謎はすぐ近くにあったのです。 何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。 加納朋子 ななつのこ より |
加納朋子の「ななつのこ」という小説を読んだ。創元推理文庫から出ているのだから、ミステリといっても良いだろう。私の好きな北村薫の「空飛ぶ馬」に始まる「円紫さんと私」シリーズによく似た雰囲気を持つ本である。
それを読んで、ふと思い出した。
私が通っていたM高校の話だ。M高校は武蔵野の玉川上水のほとりにある。
そのことを聞いたのは月曜の朝だ。日曜日の昼間に変質者が現れたというのである。目撃した人によれば、変質者は生徒用の上履きを履いていて、手には白い布を持っていたという。顔などはよくわからなかったそうだ。目撃者に驚いた変質者は逃げてしまい、白い布を落としていった、というのだ。
それだけなら、「単なる変な奴がいた」ということで話は終わった筈だ。問題は、その白い布に麻酔薬が含ませてあったという点だった。悪ふざけではすまない。
私は友人の鴨志田とその事件について話をしていた。気になることがあったからだ。変質者が目撃された場所が問題だったのだ。図に描くとこんな感じだ。
 |
 |
そこは2階の中では職員室から一番遠い。一番校門に近い玄関を揚がった所である。そして、生物室の隣だった。
生物室は、普通の教室とは違う。通常は鍵がかかっているし、それは鍵がかけられるということでもある。
生物部の部長・副部長は生物室の鍵を使える立場にあった。そして、鴨志田は生物部の部長だった。
「変質者は生物室に出入りできる奴かな?」これはどうにも重大な問題だったのである。
「生物の部長・副部長経験者ってこと?」
「うーん。」
「麻酔薬ってクロロホルムとか、かな?」と鴨志田にぼくが言うと、「立て板に水」状態で、彼の推論を聞かせてくれた。
「いや、きっとエーテルだね。」なるほど説得力はある。いや、ありすぎるといっても良い程だ。コイツ、むちゃくちゃ怪しいヤツである。犯人候補No.1である。一朝一夕で考えた理屈とは思えない。
「今時、クロロホルムなんて使われていないんだよ。」
「副作用もあるしさ。」
「あと、沸点を考えてみろよ。」
「エーテル、つまりジエチルエーテルDiethyl Ether ( (C2H5)2O )は沸点が34.6℃だ。」
「それに対して、クロロホルムChloroform ( CHCl3 )は沸点が61.7℃だ。」
「ハンカチにクロロホルムを含ませて顔に当ててもなにもおきない。」
「だけど、エーテルは人間の顔にあてたら、体温のせいで瞬間的に気化するんだよ。」
「つまり、エーテルの気体で顔の周りが覆われるわけだ。」
「呼吸なんかしたらエーテルを吸わざるをえないだろ。」
「だから、クロロホルムとかよりエーテルのほうが、変な用途には向いているんじゃないかな。」
「もっとも、即座に気を失うとは思えないけどね。」
「そういうことって生物部の部員ならみんなわかるもの?」と聞くと、
「部長・副部長をやるくらいの人は確実にわかる。けど、他の人でもわかるやつはきっと多いよ。」また、部長・副部長経験者である。
「ところで、生物室にエーテルはある?」と訊くと、
「うん、あるよ。」とのお答え。やはり、生物室の「鍵」である。
「生物室に入れる人なら手に入ると思うよ。」
「せめて靴の先の色がわかれば。」そう靴の先の色は赤・黄・緑と色分けされており、それで1,2,3年生の区別がつくのだ。もっとも、それと関係ないサンダルを履いている人のほうが実際は多いのであるが。それに、靴を履いていたから学内の生徒とは限らないが。
「学年がわかるね。」
次に、ぼくらは覚えたばかりの数学の知識をひけらかす(まだ高校生だから)話をしていた。
犯人(変質者)の条件
- 男
- 生徒用の上履きを履いてた。
- 麻酔薬に関する知識がある。
- 麻酔薬を手に入れられる。
- 生物室に入れる。
- 一人
ここで、私は
「ぼくは生物室の鍵を持っていないから、必要条件を満たしていないな。」
つまり、「生物室に入れる=鍵を使える=生物の部長・副部長経験者」であるから、「ぼくは必要条件のひとつを満たしていない」と主張したのだが、鴨志田は聞き入れなかった。。
「オマエに鍵なんか必要ないだろう。」
そう、物理部の部長(私のこと)になるには「錠前破りが得意」でなければならなかったのである。すなわち、物理部の部長経験者であると「生物室に入れる。」ということの「十分条件」をもれなく手にしてしまうのである。イヤーなおまけである。もっとも、私は生物・化学は苦手であるので、必要条件を満たしていない。
一方犯人の「十分条件」を考えてみるとこんなものがある。
- 生物部の部長・副部長
 |
「ところで、こんなミステリがあったらどう思う? 探偵がめちゃくちゃ論理的なヤツでさ。」さてさて、普通ならばここに「読者への挑戦状」が入るところだろう。だから、この話にも入れてみる。ただ、少し定型とは違う。
「コンパクト群の表現論なんかで語られてさ。」
「犯人を指摘する所なんか、数式だらけな話。」
「作家はMathematicaをワープロ代わりにしててさ。」
「......なんか、一般受けしそうにないな...おれにすら面白くないぞ...」
| ここまでに、犯人を示す証拠が全ての証拠がそろっているとは思わないし、そもそも、犯人が登場しているかどうかすら私にはわからない。いや、実際のところ登場していないと100%確信している。しかし、名探偵のあなたなら、きっと犯人を指摘してくれるに違いない。私と鴨志田の懸念を吹き飛ばしてくれるに違いない、と思うのだ。 犯人は一体誰なのだ... |
1999-11-13[n年前へ]
■やっぱり、ウニが好き ! 
Dr.フラーはウニの夢を見るか?
私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。と、始めると
の間違いと思われるかもしれない。しかし、それは違う。今回は、ウニとドームハウスの共通点について、考えてみたい。ただ、かなりビールが脳みそにしみているせいか、少しドンデモ話になるかもしれない。そこは、「ビックエッグの力学」と共通である。 私の中では、野球観戦と言えば、ビールだ。野球にはビールが良く似合う。そして、今現在も目の前にはビールがある。そして、寿司がある。といっても、スーパーで買った安物である。二つ合わせても1000円にしかならない。
 |  |
安物といっても、私の住んでいるのが港町だから安い、ということもある。何しろ、ほとんどのスーパーの魚売り場でイルカの肉なども置いてあるのだ。嘘ではない。ホントにホントである。私も、引っ越してきた当時はビックリしたが、本当である。アメリカの動物愛護団体が見たらびっくりの風景だろう。「イルカと人間はお友達」と言ってる人には見せられない風景だ。
あまりおいしそうではないので、私はまだ実際に味わってはいない。しかし、地元の人の中には「よく食べる」と言う人もいる。いつか、挑戦してみたい。
さて、上の写真で共通しているのはウニである。ウニと言えば、こんな姿をしている。
 |
「海栗」と書いてウニと読むことが実に納得できる姿である。しかし、内面はもう少し違う。実は、ウニはドームにそっくりである。前回考えたドーム球場ではないが、ウニは実はドーム構造をしているのだ。「そんなことは当たり前じゃないか」と言う人もいるだろう。しかし、私はつい最近までそれを知らなかった。そもそも、骨があるとすら思っていなかったのである。
もしかしたら、私のようにウニの内面を知らない人もいるかもしれない(そんな人はいない、という声も聞こえそうだが)。そこで、ウニの骨の写真を示してみる。下に示すのが、色々なウニの骨だ。
 実物はとてもきれい。日本古来の木工細工のような穴がとてもきれいである。 |
これは少し前に、宇宙科学研究所の黒谷氏の実験室を見学(ただ邪魔しただけという気もするのであるが)する機会があり、そのとき頂いたものである。最初に見たときは、「目からウロコ」であった。まさか、あの針の山の下にこんな頑丈な殻が存在しているとは、思わなかった。
写真ではわからないかもしれないが、骨には小さな穴が極めて規則的に開いている。それが、日本古来のとても出来がいい木工細工のようである。光に透かしてみると、うっとりするようなきれいさである。内部に強い光源でもおけば、プラネタリウムやミラーボールみたいに細い光線を放射する、きれいなアクセサリーができそうだ。
ところで、「何故、宇宙科学研究所の実験室にウニが?」と思われる方は、WEBで検索でもかけてみると良いかもしれない。「宇宙生物学」という面白い実験分野があるものだ。
例えば、無重力の中で生物がどのような挙動を示すか、などの研究をしたりするらしい。飛行機にのってそういう実験を繰り返すわけである。遊園地のフリーファールやバンジージャンプ、そして、ジェットコースターでさえ、駄目な私には地獄のような研究分野である。
さて、上の、ウニの骨の姿はまさにドームそのもの、とは思えないだろうか? そう、似ているのだ。 そっくりなのだ。試しに、このドームなどを見れば納得できるだろう。
 |
これは、富士山頂の厳しい環境を耐えるために、極めて安定なドーム構造が用いられているのだ。三角形のパネルが組み合わさるドームハウスは極めて頑丈である。ウニも、同じように頑丈なドーム構造の骨格を持っているのである。レーダードームは富士山頂で頑張っているが、宇宙科学研究所のウニは色々なところへ連れて行かれて、厳しい実験に耐えているのである。
こういった、ドームと言えば、R.バックミンスター・フラー博士のドーム理論だろう。フラー博士とドームハウスのスケッチ図を示してみる。
|
よく、環境適応性の高さを謳うことの多いドームハウスであるが、もしかしたら、ウニがその祖先であるかもしれない。もしかしたら、フラー博士は「海の中でじっとたたずむウニの夢を見て」ドームハウスを思いついたのかもしれない。
アメリカ人であるフラー博士がウニを食べたとは思えない、という人も多いだろう。それは確かにその通りである。しかし、フラー博士はかなりの変人である。変人ならば、ウニを食べまくっていたとしても、おかしくはない。
普段は「何を馬鹿な発想だ」と思うことだろう。しかし、ドーム球場の野球を見ながら、脳みそがビールとウニで満たされてしまうと、「そうだ、フラー博士はウニが大好きなのだ!そうに違いない!」と確信してしまうのだ。
仮に、フラー博士がウニに影響されていないとしても、ウニはフラー博士がドーム理論を考えるずっと太古の昔から、ドーム構造をしていたのである。ならば、「元祖はやはりウニなのだ!」と言ってしまって良いだろう。太古から厳しい環境を耐えつづけてきたウニは、今や宇宙へ飛び出し、さらに厳しい環境の中で活躍しているのである。
1999-12-19[n年前へ]
■母に捧げるバラード 
宿題は自分でやってくれぇ
今回の話は、とあるメーリングリストから始まる。仮にそのメーリングリストを"family-ml"と名付けておく。そのfamily-mlで論争が起きたのである。
メーリングリストで論争が起きることはよくある。しかし、このfamily-mlは通常のメーリングリストではなかった。実は、とある家族を構成員とするものであった。そう、この家族は専用のメーリングリストを持っているのである。そこで、この論争は起きた。
各登場人物の紹介は随時していこうと思う。
| To family-**@hirax.net From 母 Subject: レポート課題がわからない みなさんお元気ですね。 大気の持つ質量あたりのエネルギーを、次の二つの例について求めなさい。 「下」 赤道付近の地表面付近の大気 「上」 赤道付近り対流圏界面付近の大気 結果を次のような表にまとめなさい。 さて、インドの話はいらしたときにします。大変な国ですが、行って良かったです。 母 |
この「母」はいまはやりのヤンママではない。戦中に生まれたお年の方である。去年辺りから仕事のない日に大学へ社会人学生として通うようになったのである。
| To family-**@hirax.net From 兄 Subject:Re: レポート課題がわからない > レポート課題 SOSです。だれか教えて下さい。 この「母」のレポートって「弟」の得意な専門の問題じゃないの? > 高さ 1500m(=15Km) あと、15000mの間違い? 兄 |
「兄」はとあるWEBのwebmasterである。「母」の年からすれば、そうそう若くもないことがわかる。
| To family-**@hirax.net From 父 Subject:Re: レポート課題がわからない >結果を次のような表にまとめなさい。 父 |
「父」はhiraxという名前を数十年名乗ってきた、元祖hiraxである。
| To family-**@hirax.net From 母 Subject:Re: レポート課題がわからない 今年は地球科学概論をとった。確か昨年「兄」が次は地球科学がいいと、 母 |
確か、この「母」は去年は「応用化学」をとっていた。なぜ、そういう無理なことをしたがるのだ。
気持ちはわからないでもないが、もう少し考えて欲しいものである。
| To family-**@hirax.net From 兄 Subject:Re: レポート課題がわからない > 今年は地球科学概論をとった。確か昨年「兄」が次は地球科学がいいと、 いや、私が言ったのは「どうせ習うなら自然科学史みたいなのの方がいいよ。」です。「地球科学概論」だなんて言っておりません。 >自分の責任のあることを「弟」に振ろうとしていませんか。 いや、私に責任はないと思うのですが... >だれでもいいです。「弟」、助けてくれますか? そうそう > 「弟」 兄 |
| To family-**@hirax.net From 弟 Subject:Re: レポート課題がわからない >そうそう > 「弟」 地球科学概論なんだから、宇宙・地球物理専攻の人がやるべき 最近、修論のまとめで忙しいです。 弟 |
| To family-**@hirax.net From 兄 Subject:Re: レポート課題がわからない > 地球科学概論なんだから、宇宙・地球物理専攻の人がやるべき しかし、これってほとんど化学工学ではないでしょうか。だから、 兄 |
| To family-**@hirax.net From 母 Subject:Re: レポート課題がわからない >>> そうそう助けてやれよ > 「弟」 そろいもそろって、冷たい兄弟ですね。 母 |
うちの「母」はこうなると怖い。
| To family-**@hirax.net From 「妹姉」 Subject:Re: レポート課題がわからない >>>> そうそう助けてやれよ > 「弟」 >そろいもそろって、冷たい兄弟ですね。 そういうと、私まで一緒みたいに聞こえます。やめて下さい。兄妹とか姉弟 「妹姉」 |
| To family-**@hirax.net From 父 Subject:Re: レポート課題がわからない 「母」がせっかく苦労してレポートをと考えているので、hiraxファミリーの 多分、「兄」や「弟」だったら、チョチョイだから。 > どうせ習うなら自然科学史みたいなものの方がいいよ。 父 |
| To family-**@hirax.net From 兄 Subject:Re: レポート課題がわからない >多分、「兄」や「弟」だったら、チョチョイだから。 >今朝、「父」は物理的な意味だけは、10分間講義してあげました。 そんなに若くはない年で働きながらも、大学へ行こうとする「母」の 兄 |
さて、配達された最後の手紙が以下である。
| To family-**@hirax.net From 兄 Subject:Re: レポート課題がわからない 昨日の電話など、何やらプレッシャーが感じられてきたので、適当に問題にとりかかって まずは、簡単そうな位置エネルギーと運動エネルギーから。「地球科学概論」 「問題」 「上」 赤道付近り対流圏界面付近の大気 「上」「下」それぞれについて 「回答」 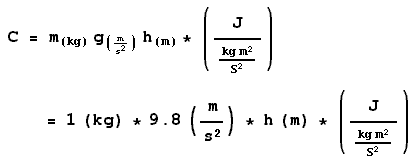 「上」 赤道付近り対流圏界面付近の大気 h=15000(m) 「下」 赤道付近の地表面付近の大気 h=0(m) を代入し、 「上」 1.47*10^(5) J 「下」 0 J を得る。 運動エネルギーDは速度v(m/s)に対して、 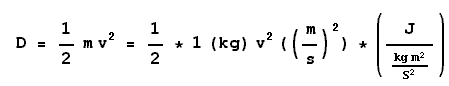 「上」 赤道付近り対流圏界面付近の大気 v=20(m/s) 「下」 赤道付近の地表面付近の大気 v=5(m/s) を代入し、 「上」 200 J 「下」 12.5 J を得る。 さて、次に「A.内部エネルギーの温度に比例する部分、B.内部エネルギーの水蒸気に比例する部分」 「上」 赤道付近り対流圏界面付近の大気 (300-6×15)K 最後に「B.内部エネルギーの水蒸気に比例する部分」であるが、水が液体から気体に変化するときのエネルギー収支を考る。蒸発熱が2498J/gであることを考え、計算を行う。 「上」 赤道付近り対流圏界面付近の大気 水蒸気0g なお、検算も読み直しもしておりません。 兄 |
ごくまれにではあるが、「課題を解いてください」という大学生からのメールが届くことがある。そういうメールを見るたびに「うーむ...」という気分になっていたのである。しかし、まさか自分の親の宿題をやるはめになるとは。しかもこの年になって...
1999-12-21[n年前へ]
■恋の力学 
恋の無限摂動
クリスマスが近くなると、街のイルミネーションが綺麗に輝き始める。いかにも、ラブストーリーが似合う季節である。そこで、今回は、"Powerof love"、すなわち、「恋の力」について考えてみたいと思う。「恋の力」により、人がどのような力を受け、人がどう束縛されるのか、などについて考えみたいのである。また、恋に落ちたカップルがどのような行動をするのかについて解析を行ってみたい。
「できるかな?」では以前、
において、カップルが他のカップルを意識する力について考えたことがある。カップル同士の間に働く斥力を考えることにより、鴨川カップルの行動を考えてみた。それと同様に、今回はひとつのカップルのみを考え、その中に働く力を考えてみるのである。ひとつのカップルの「男」と「女」の間にどのような力が働くかを考えるのである。そういうわけで、今回の登場人物は「男」と「女」である。その二人は「恋に落ちた二人」である。二人の間には「恋の力」が働いているのだ。その二人の間に働く「恋の力」について考察することにより、恋に落ちたカップルの行動について考察を行ってみることにする。
といっても、「恋の力」を精密に測定した報告例は未だ存在しないので、ここでは適当な値を用いていくことにする。「恋は距離に負けない」とか「遠くて近きは男女の仲」などとははよく言われる。そこで、距離によらないと近似した。また、「遠くて近きは男女の仲」の意味を考えれば、恋の力は無限遠まで働く力である、と考えるのが自然である。
そこで、今回の「恋の力」は距離に関わらず一定であると仮定した。距離=rとした時に-r/Abs[r]の大きさで「相手に惹かれる」ものとした。仮に第一種「恋の力」(仮称)とでもしておく。
今回は「恋の力」は距離によらないものとした。しかし実際は、(通所の距離においては)「男」と「女」は距離が近いほど惹かれ合うし、離れてしまうと惹かれ合う力は弱くなるというのが自然であると思われる。そこで今回の第一種「恋の力」(仮称)は、あくまで大雑把な近似ということにしておく。
恋する二人の間に働く力をもう少し正確に記述しておくと、
- 「恋の力」 = - 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「恋の力」=優柔不断度 * 「恋の加速度」
であることだ。心がトキメいてもなかなか行動を起こすことが出来ない人がいるだろう。そういう人は「優柔不断度」が高いというわけである。恋の行動における慣性を示すパラメータである。
また、今回は空間を1次元であると簡略化してみた。1次元の空間の中で「男」と「女」が動き回るのである。その時間的変化を調べてみるのだ。従って、シミュレーション結果は空間軸が一次元+時間軸一次元で、合わせて2次元となる。
さて、この「恋の運動方程式」を解くことにより、恋する二人の行動は予測することが可能となるわけだ。試しに、その計算サンプルを示してみる。なお、今回は時間方向で数値的に逐次解を求めている。
初期状態は
- 「男」位置=5, 速度=0,魅力=100,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
位置や時間の単位は任意単位である。「0」と「5」は東京と大阪であっても良いし、ロンドンとニューヨークであっても良い。あるいは、実空間でなく精神的な空間と考えてもらっても構わない。すなわち、心の動きを示しているものとするのである。
また、二人の「魅力」や「優柔不断度」は対等である場合だ。その結果を下に示す。このグラフは縦軸が空間位置であり、横軸が時間である。黒線が「男」であり、赤線が「女」である。
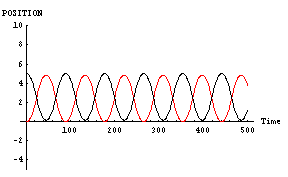 |
「男」と「女」が同じように相手の方向へ向かっているのがわかると思う。これが「恋の無限摂動」である。こういった「恋の無限摂動」の代表的なものには「君の名は」の主人公達の動きなどがある。恋に落ちた二人が、延々とすれ違いを続ける物語である。これは、この「男」と「女」の行動そのものである。
この計算結果では「男」と「女」が糸を紡いでいるようにうまく絡みあっているのがわかる。「恋の無限摂動」の幸せなパターン例である。これは、「男」と「女」が対等であったことがその一因である。
その証拠に、「男」と「女」が対等でない場合の計算結果を示してみる。次に示すのは、
- 「男」位置=5, 速度=0,魅力=10,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
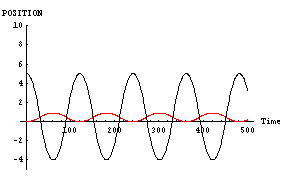 |
「男」が右往左往するのに対して、「女」はほとんど動いていないのがわかると思う。おそらく、この場合には「男」と「女」の「心」もこれと同様のパターンを示しているものと思われる。すなわち、「男」の「心」は揺れ動いているのに対し、「女」の「心」はほとんど動いていないのである。
先の例と異なり、これは実に不幸な計算例である。不幸ではあるが実際によくある例であると思う。以降、これを「男はつらいよ」パターンと呼ぶことにする。「女」に「男」が振り回されているパターンだ。もし、奇跡的に結婚などしても、将来どうなるかは火を見るより明らかである。
それでは、「男」と「女」の「魅力」が同等で、かつ、とてもスゴイ場合を示してみる。すなわち、ドラマの主人公達のようにとてつもなく魅力的な二人が恋に落ちた場合である。一般人とは違う二人が恋に落ちたら、果たしてどのような行動を示すのであろうか?この場合のパラメータは以下に示す、
- 「男」位置=5, 速度=0,魅力=1000,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=1000,優柔不断度=10
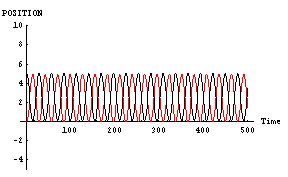 |
「魅力ある二人が恋に落ちた場合には、あまり近づかない方が良い」という教訓をここから得ることができる。
最後に、「男」と「女」の二人ともにあまり魅力がない場合である。パラメータとしては、
- 「男」位置=5, 速度=0,魅力=2,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=2,優柔不断度=10
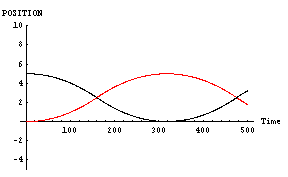 |
これなど「恋」と言えるのかどうかもわからない位である。ほとんど、「ただすれ違っただけの相手」である。これがさらに進むと、魅力がお互いに0同士のパターン、
- 「男」位置=5, 速度=0,魅力=0,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=0,優柔不断度=10
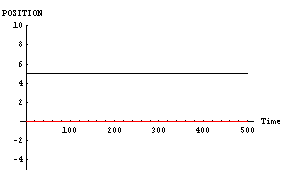 |
これっぽっちも「男」と「女」は「恋」に落ちていないのである。これではカップルの「男」と「女」ではなく、単なる他人である。
さて、今回は行わなかったが、カップルに「恋のエネルギー損失」を導入することにより、「恋の無限摂動」を減衰させることができる。それにより、現実のカップルの行動にさらに近づくことができるのではないかと、私は考える。何らかの抵抗が生じることにより、「恋の無限摂動」が減衰するのだ。そして、二人は接近した状態で停止するわけだ。
さて、今回の登場人物は「男」と「女」だけであった。しかし、現実でも、ドラマの中でも、通常は多くの登場人物が登場する。登場人物が「男」と「女」だけというような理想的な条件のみではない。
人の恋路を邪魔する(主人公からすれば)ヤツも必ず登場する。また、特定の登場人物の間では斥力が働くだろう。そのような場合、一体どのような現象が生じるのだろうか。
そもそも、今回の恋する二人の行動パターンは予測可能であったが、現実そのようなことがあるだろうか?果たして、未来の行動パターンは予測可能なのだろうか?色々な登場人物が現れる場合にも、今回の結論は成立するのだろうか?
それらは次回の課題にしておく。題して、「恋の力学 三角関係編- 恋の三体問題- (仮称)」である。「恋の力」を一般化し、多体問題として解いてみたいのである。恋する人達とその周りの人達がどのような行動をするか、恋の三角関係においてどのような力が働いているのか、について解析を行ってみたい。今回は、そのための前準備というわけである。
1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
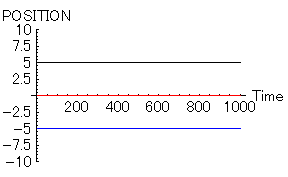 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
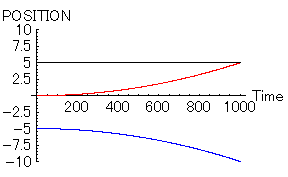 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
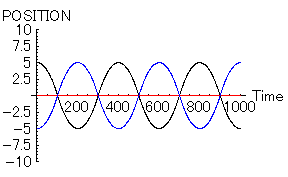 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
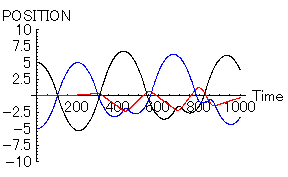 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)

