hirax.net::Keywords::「探し」のブログ

■"Sanae chan"はもういない　

Sanae chan was fluid in the net news

- Sanae-chan was fluid in the net news -

　「大学ノートにさなえちゃんを画いたのに、消えてしまった。」という歌があると聞いたのですが、誰のどんな名前の歌だったか教えて下さい、という疑問がfj.questions.misc辺りで出されたことがあった。
　その疑問に対して、

「私も歌った記憶がある」
「ずいぶん昔の歌であやふやだが、大学ノートの裏表紙に、サナエちゃんを書いたの、で始まっていた。」
「それは古井戸の曲だろう。」
「RCサクセションの「僕の好きな先生」と雰囲気がよく似ていた。」
「さなえちゃんが入っているアルバムはどれだろう？」

などと、その人なりの「さなえちゃん」が記事として次々と流れた。その人の記憶の中での歌詞が数多く投稿された。しかし、どれも少しずつ、あるいは、かなり違った歌詞になっていた。時が流れる中で、その人の「さなえちゃん」の記憶が変化していたのである。
　それは、今で言うコラボレーションだったように思う。
　多くの人がその人なりの「さなえちゃん」を描く中で、「さなえちゃん」の姿が時々見えたような気がした。歌詞の中の「さなえちゃん」の色々な本当の姿が見えたようにすら感じた。その一連の記事を読んでいると、まるで短編小説を読んでいるように、私には思われた。しかも、net news という大学ノートよりも消えやすい一過性のものであるのが、なおさら新鮮だった。

　今日急に、もう一度、その一連の記事を読みたくなった。もしかしたら、過去にnet newsで流れた記事をストックしている所もあるかもしれない。

　すると、NetNewsArchive(http://mitsuko.jaist.ac.jp/fj/)という所が見つかった。そこで、NetNewsArchive(http://mitsuko.jaist.ac.jp/fj/)で探してみた。見つからないかもしれない、とあきらめていたが、見つかった。ftp://ftp.jaist.ac.jp/pub/news-archive/fj.questions.misc/List-199401にあった。[song]sanaechanというタイトルで始まるスレッドである。

　調べる中で、SeagaleMusic Webから歌詞を知ることができた。そのラストの歌詞は、とてもいいと思う。また、面白いことも知った。カトーカズヒロの70年代なつかし音楽談話室（9）によれば古井戸はアルファベットでは"fluid"と書くそうだ。流体、流動体のことである。また、形容詞ならば、流れていく、変わりやすい、などの意味になる。

最近とあるマンガで昔あった曲として「さなえちゃん」というのが登場してました。内容はほとんど不明ですが、最後にさなえちゃんは消えちゃうんだそうです。作者の後書きによればこれはマンガの創作ではなく実在する曲らしいのですが、どなたかご存知ないでしょうか？

　結構はやった歌ですね。「大学ノートの裏表紙、さなえちゃんを書いたの...」で始まる歌だったと思います。非常に短かったような気がします。歌詞は、「大学ノートの裏表紙に、サナエちゃんを書いたの。」で始まる奴でいいのですか。浅田美代子の「赤い風船」の時代ですね。４０代の人が知っているはずですね。課長とかに聞いてみたら？

　えーと、"大学ノートの裏表紙にさなえちゃんを書いたの"という曲でしたか、記憶があります。昔のフォーク全盛期のころの曲で、歌っているのは、すんごく不確かな記憶ですが、"古井戸"ではなかったでしょうか。

　古井戸の「さなえちゃん」ですね．15, 6 年前(もう少し前かな?)の曲です．大学ノート裏表紙に書いたさなえちゃんが，消えてしまったというただそれだけの曲ですが，なぜかこころに残ってしまふ．古井戸の「ベストアルバム」のCD にはフルコーラスは入っていなかったと思うので，CD で出ているかどうかは知りません．

　1971年か72年頃に流行った歌で、古井戸の「さなえちゃん」だと思います。確か仲井戸麗市さんと誰かの二人組のグループだったのでは。「♪大学ノートの裏表紙に」鉛筆で描いたため、(うまく描けたのに)いつの間にか(絵が)消えちゃうんだと思います。
# グループ名、メンバーはちがうかもしれません。
# RCサクセションの「僕の好きな先生」と記憶がゴッチャになってます_o_

　以下はかなり曖昧な記憶なので、そのつもりで読んでください。古井戸の「さなえちゃん」が収録されているアルバムはCD化されていますが、そのCDを外から見たかぎりでは「さなえちゃん」が入っていることは分かりません。他の曲は収録曲として書かれているのですが、「さなえちゃん」だけは、古井戸の意向でわざと書かれていないからです。ただしCDを聞けば、曲自体はLPと同様に収録されています。したがって収録アルバムのタイトルが分からないと、それを探しだすことは出来ません。「さなえちゃん」の入ったアルバムを昔持ってたのですが，なくしてしまったのでタイトルは確認できないのですが，ジャケットは薄暗い色(暗い灰色?，モノクロ?)だったような気がします．

　なんて古い曲なのでしょう。わかってしまう、自分が悲しかったりして...兄がよく歌っていた曲です。このころ、ガロの”学生街の喫茶店”もはやっていたと思います。歌詞は、 記憶の奥をたどって、 大学ノートの裏表紙に、サナエちゃんを書いたの。 一日中かかって、一生懸命書いたの。 でも、鉛筆で書いたから、いつの間にか消えたの。 大学ノートの裏表紙の、さなえちゃんは、消えたの...

　その歌の中にいた「さなえちゃん」は、「さなえちゃんが消えたの。もう会えないの。二度と会えないの」と歌われていた。"fluid"が必ずそうであるように、newsgroupに流れた記事もすぐに流れていってしまった。news groupに現れた"sanae chan"はもういない。

■宇宙人はどこにいる?　

画像復元を勉強してみたい その1

　知人から「自称UFO写真」というのものが冗談半分(いや100%位か)で送られてきた。その写真はボケボケの画像なので何がなんだかなんだかわからない。そこで、ぼけぼけ画像を復元する方法を勉強してみたい。UFOは冗談として、画像復元において進んでいるのは天文分野である。そこで、このようなタイトルなのである。もちろん、画像復元の問題は奥が深すぎるので、じっくりと時間をかけてみる。今回はMathematicaを使って試行錯誤を行った。

　ボケ画像を復元するには、ボケ画像がどのように出来ているかを考えなければならない。そこで、ごく単純なぼけ画像を考えてみる。まずは以下の画像のような場合である。

左の点画像が右のようにボケる

画像:1

画像:2

　右の点画像が何らかの理由で右の画像のようにボケる場合だ。焦点のボケた写真などはこんな感じだろう。例えば、これはレンズの焦点合わせがおかしいカメラの画像だと思ってみる。そのカメラで風景を撮るとこのようになる。

本来、左のような風景がボケて右の写真のようになる。

画像:3

画像:4

　偶然、写真にカメラが写っているが、偶然である。別にそのカメラが焦点がボケボケといっているわけではない。今回、やりたいことは右上の写真(画像:4)を元に、左上の写真(画像:3)を復元したいということである。

　画像:1のような点画像が、画像:2のような分布のボケ画像になるとすると、次のような関係が成り立つ。

(式:1) 画像:4 = 画像:3 * 画像:2

画像:1のような点画像が画像:2になるなら、それを参照すれば、画像:3のような点画像の集合がどう
ボケるかは計算できる。つまり、それが画像:4になる。ここで、*はコンボリューションを表している。
　よくある信号処理の話で言えば、画像:2はインパルス応答である。といっても、これはごくごく単純な場合(線形シフトインバリアントとかいろいろ条件がある)の話である。まずはそういう簡単な場合から始めてみる。

　このようなごく単純な場合には

(式:2) 画像:3 = 画像:4 * (1/画像:2)

とすれば、画像:3を復元できることになる。

そこで、まずは単純な1次元データで考える。下の画像:5のようにボケる場合を考える。ここでは、ガウス分布にボケるようにしてある。

赤い線で表したパルスデータが水色で表した分布にボケる

画像:5

(式:1より) ボケ画像 = オリジナル画像 * ボケ具合
であったが、* すなわち、コンボリューションは
逆フーリエ変換(フーリエ変換(オリジナル画像) x フーリエ変換(ボケ具合))
と表すことができる。つまり、周波数領域で掛け算をすれば良いわけである。

左がボケ画像、右がその周波数領域(フーリエ変換)

画像:6

画像:7

　右のボケ画像の周波数表示を見れば低周波数の量が多いのがわかる。結局、このモデルではボケると低周波数を増やすことになる。逆に(式:2)では高周波数の量を増やすことに相当する。だから、Photoshopなどの「シャープ」というプラグインはラプラシアンを用いて、高周波を増やしてやることでボケ低減を行っている。それほど、不自然ではない。しかし、そう近い画像復元ができるわけでもない。

　それでは、試しに適当な1次元データをつくって、画像:6とコンボリューションをとってやり、ボケさせてみる。

左が原画像、右が画像:6と画像:8のコンボリューションをとったボケ画像

画像:8

画像:9

　画像:8のパルスデータは、画像:9ではボケてしまい、判別不能である。そこで、

逆フーリエ変換(フーリエ変換(画像:9) / フーリエ変換(画像:7))

= InverseFourier[Fourier[Image8] / Fourier[Image6]]; (*Mathematica*)

とやると、次のデータが得られる。

復元されたデータ

画像:10

　これがインバースフィルターによる画像復元の方法である。FIR(Finite InpulseResponse)フィルタなどだろう。ところで、

(式:2) 画像:3 = 画像:4 * (1/画像:2)

を見るとわかるが、画像:2が周波数領域で0になる点があったりすると、計算することができない。また、0に近いとむやみな高周波数の増幅が行われて使えない。

　そこで、この方法の修正として、ウィーナフィルターなどの最小平均自乗誤差フィルターがある。これにも多くの不自然な条件のもとに計算される(らしい)。しかし、infoseek辺りで探した限りでは、ウィーナフィルターを用いた画像復元の標準であるらしい。

この方法は先の逆変換に対して、次のように変形されたものである。Mathematicaの表記をそのまま貼り付けたのでわかりにくいかもしれない。

Noise ノイズのパワースペクトル
Signal 信号のパワースペクトル
Boke ボケる様子のインパルス応答
Conjugate 複素共役
BokeData ボケ画像
ResData1 計算した復元画像

Boke1 = (Boke^2 + Noise/Signal)/Conjugate[Boke]; (*Mathematica*)
ResData1 = InverseFourier[Fourier[BokeData] / Fourier[Boke1]]; (*Mathematica*)

である。Noise/SignalはS/N比の逆数であるから、SN比の大きいところではインバースフィルターに近づく。また、インバースフィルターの計算不能な点が消えている。

　これを使って復元してみたのが、次のデータである。

ウィーナフィルターを用いた復元

画像:11

　他にも、いろいろ変形っぽいものがあるが、とりあえず、1次元での練習はここまでにして、2次元で画像復元を行ってみる。

　まずは、ボケのフィルター(PSF=PointSpreadFunction(どのようにボケるかを示すもの)、2次元のインパルス応答)である。

ボケのフィルター(インパルス応答)

画像:12

　それでは、画像をボケさせる。右のボケ画像が全体的に暗いのは左とレンジが表示の違うからである。同じレンジにすると真っ白(真ん中辺りはちょっと灰色)になる。

左がオリジナル画像、右はボケた画像

画像:13

画像:14

　それでは、インバースフィルターを用いて画像を復元させてみる。

復元した画像

　うまく再現できている。今回はノイズも混入していないしPSF(PointSpreadFunction)もわかっているのだから、復元できて当然である。他の射影フィルタ、最大エントロピー・フィルタ、一般逆行列法、SVD法等については今回はまだ挑戦してみていない。
　その他線形の画像復元法をいくつか調べたが、ウィーナフィルターやインバースフィルターとほとんど同じような物が(素人目には)多かった。そこで、ウィーナフィルタなどとはやり方がかなり異なるものについて、いずれ挑戦してみたい。

　関係はないが、ウィナーと言えばサイバネティクスが思い浮かんでしまう。当然、ロゲルギストが連想されるわけだが、文庫本か何かで岩波版と中公版の「物理の散歩道」が安く売り出されないのだろうか？売れると思うんだけど。新書版は高すぎる。

　宇宙人はどこにいるか? そういった話は専門家に聞いて欲しい。わからないとは思うが。

................................................................................

　さて、ここからは、1999.01.24に書いている。シンクロニシティとでも言うのか、今回の一週間後の1999.01.17に
日本テレビ系『特命リサーチ200X』で

地球外生命体は存在するのか？( http://www.ntv.co.jp/FERC/research/19990117/f0220.html )

という回があった。何とこの回のコメンテーターは先の専門家と同じなのだ。偶然とは面白いものだ。

■感温液晶でNotePCの発熱分布を可視化する　

熱いところで感じてみたい St.Valentine 記念

東急ハンズで実験材料をいくつか買った。その中から、感温液晶シートを使って計測を行ってみたい。
色が変わる材料というものは多い。温度により物質の色がかわる現象はサーモクロミズムと呼ばれる。光により色が変わるサングラスのような現象の場合はフォトクロミズム呼ばれる。けっこう、色々な応用を見かける。
通常の感温液晶はコレステリック(Cholesteric)効果により反射光のスペクトルが変わるため、色が変化する。

これが感温液晶シートである。よくで見かけると思う。

感温液晶シート

さて、それでは感温液晶を使っていくつか測定を行ってみたい。まずは、NotePCの発熱分布を調べてみる。最近のNotePCはかなり熱くなるものが多い。暖かいというよりもアッチッチ状態になるものさえある。

それでは、

• Toshiba Libretto50
• Panasonic Let'sNote mini(AL-N4)

の2つで発熱分布を調べてみたい。

いずれも、感温液晶シートをNotePCの上に載せることにより、評価を行っている。今回は発熱分布を知ることが目的であるので定量的な評価は行っていない。もし、温度を定量的に行いたいのであれば、色と温度の対応曲線をあらかじめ測定する必要がある。

以下に結果を示す。

Libretto 50

	左上：上面 右上：上面の発熱分布 左下：下面の発熱分布

Panasonic Let'sNote mini (AL-N4)

	左上：上面 右上：上面の発熱分布 左下：下面の発熱分布 感温液晶シートのサイズがA4であるため、Let'sNote miniにちょうどフィットする。

Libretto50ではPCカードのNICを右に挿しているため、キーボードの右側部分の発熱が大きい。また、下面ではハードディスク部分の発熱がわかる。また、ク＊ックア＊プしているせいかかなりアッチッチである。
Libretto50,Let's Note miniいずれにおいても液晶のドライバーがある部分(液晶の左)は発熱が激しいのがわかる。

本来ならば、愛用しているTOSHIBA Portege320でも計測を行いたい所だが、ただいま長期入院中である。間もなく使用1年になるが、これまでに入院3回を経験し、入院期間は計2ヶ月にわたる。昔の小説家もビックリの病弱さである。他の使用者の話を聞いていても実に不安定な機種のようだ。一体、疲労骨折を経験していないPortege320というのは、はたして存在するのだろうか。あぁ...

今回は手元にあったNotePCでのみ測定を行ったが、近所の協力の下に色々なNotePCの発熱分布を調べる予定である。特にパームレスト周りの発熱分布などは割に軽んじられているだけに、興味がある。

今回は感温液晶を使った温度分布の簡単な可視化をしてみた。同じような測定は色々してみる予定である。

感温液晶と同じように、温度で変化する材料は多い。例えば、FAXでよく使用される感熱紙もそうである。
他にも、RICOHの熱可逆性情報表示フィルム
http://ext.ricoh.co.jp/saiyo/sin/prof/eyes/page4_2.html
などもそうである。
これなどはお店のポイントカードなどでよく見掛ける。私の財布から探してみると、オートバックスのポイントカードがこれと同じようなものである。70-130℃位の温度変化により透明度を変化させる材料である。これ位の温度であると、真夏の車中にカードを放置するとどうなるか心配なところである。

今回の情報に関連するWEB一覧

• 伊藤のホームページ(http://www.infonia.ne.jp/~itous/)
• 岡山県教育センター(http://www.pref.okayama.jp/kyoiku/sido/edu_cent/seminar/rika/rikasho/zikken.htm)
• お湯で変色するサーモクロミズム化合物をつくる(高橋　正）(http://www2b.biglobe.ne.jp/~murasho/news22.htm)
• 液晶について(http://www.osakac.ac.jp/labs/fujita/asai/ekisyo.html)
• 感温液晶を用いた非定常熱伝達の計測システムの基礎的研究(http://village.infoweb.ne.jp/~fwhz0564/kenkyu.htm)
• 感温液晶マイクロカプセルによる可視化(http://koneeko.linux.or.jp/AandO/gfd_exp/exp_j/tech/elc.htm)

■分数階微分に基づく画像特性を考えてみたい　

同じ年齢でも大違い

前回、分数階微分の謎 - 線形代数、分数階微分、シュレディンガー方程式の三題話- で分数階微分について調べた。例えば、0.7階微分といった、整数階でない微分である。今回はそれを使った応用を考えてみたい。

人間の視覚というものは明るいものは強く感じることができる。これは当たり前である。そして、それだけでなく、強さが変化している所にも(興味を)強く感じ取るようになっている。岡本安春氏の「Delphiでエンジョイプログラミング」によれば、そのような考えはLaming(1986)がdifferential coupling(差動結合)として発表しているらしい。

ということは、人間が画像を感じる特性というものは、画像強度と画像強度変化(画像強度の一階微分)の中間的なものであると言うことができるかもしれない。とすれば、分数階微分を導入すれば面白い表現ができるかもしれない。
今回は、そういう考えのもとに分数階微分を用いて人間の画像特性について考えてみたい。

まずは、元画像を示す。元画像はガウス分布に基づいて作成されたものである。

元画像とその鳥瞰図

まずは、左の元画像を見て欲しい。どこに強い感じを受けるだろうか？白い部分はもちろんであるが、白と黒の境界部にも強い感じを受けるだろう。ギザギザになっているのはデータが少ないからなので、無視して欲しい。というわけで、人間の視覚画像特性は

• 画像強度
• 画像強度変化(画像強度の一階微分)

というものの中間的なものと結び付けることができる(としておく、今回は)。それでは、元画像から元画像の一階微分までの間で連続的に分数階微分をしてみる。先の元画像を見たときに受けた印象と近いものが、分数階微分画像の中にあるかどうか探してみてもらいたい。

元画像から元画像の一階微分までの分数階微分画像

元画像
1/2階微分画像
15/20階微分画像
1階微分画像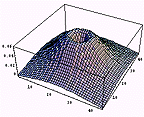

白地に黒画像バージョンも示しておく。紙の上の画像に慣れた人にはこちらの方が良いだろう。

元画像から元画像の一階微分までの分数階微分画像(白地背景)

元画像

1/2階微分画像

15/20階微分画像

1階微分画像

なお、今回の画像の作成は次のような手順で行っている。

1. 1次元のガウス分布を作成する。
2. 微分値が正であるような半分の領域を線対称に回転させ、2次元画像を作成する。

なぜ、このような方法をとっているかと言えば、微分値が負の値になる領域を除きたいからである。

今回は

• 画像強度
• 画像強度変化(画像強度の一階微分)

というものの中間的なものとして分数階微分を用いたが、これに限る話ではない。例えば、

• 電位
• 電界(電位の微分、といっても本来は電位が電界の積分か)

とか、あるいは、

• 人口密度
• 人口密度変化(人口密度の微分)

といったものでも良いだろう。今回のデータを電位とか人口密度に基づくものとして読み直せば良いだけである。色々と用途があるのかもしれないと思う。分数階微分の定義からすれば、位相遅れなどが存在する物理現象であれば、物理的な意味を厳密に持たせた上での解析ができるように思う。いずれ、音響インピーダンスなどの解析に用いてみたい。

さて、分数階微分を調べる中で、バナッハ空間についても調べた。調べ始めた時には、聞き覚えもなかったが、調べてみるとヒルベルト空間の導入で登場していた。きれいさっぱり忘れていたようである。
京大数学教室 徳永健一氏のWEB (http://www.kusm.kyoto-u.ac.jp/~kenichi/)
から辿れる「「年齢の本」数学者版」によれば
バナッハがバナッハ空間を提唱したのは30歳の時であるらしい。(http://www.kusm.kyoto-u.ac.jp/~kenichi/age/30.html)
うーん...

■fvion.icoの正体?　

不思議なログファイル

　週間ASCIIを読んでいると、InternetExplorerにユーザーのプライバシーを侵害するような機能があることが新たにわかった、という記事が載っていた。その記事中ではfavicon.icoというファイルがカギであるらしい。favicon.icoというファイル名を見てびっくりした。

　本WEBサイトが立ち上がった当初から、ログファイル中に「favicon.icoという謎のファイルを探したが見つからない」というエラーが出ていた。例えば、最近のLogで示してみると、

Top 10 of 25 Documents Not Found

Rank	URL	Accesses	%
1	/dekirukana/screensave/Image.lzh	39	30.23
2	/dekirukana/toolplus/toolp.gif	20	15.50
3	/robots.txt	16	12.40
4	/favicon.ico	14	10.85
5	/~sgsc793/index.htm	6	4.65
6	/dekirukana/java/index_e.html	5	3.88
7	/dekirukana/probe/index_e.html	5	3.88
8	/dekirukana/server/favicon.ico	2	1.55
9	/dekirukana/java/JypewriterBeanInfo.class	2	1.55
10	/dekirukana/onkai2/www.natinst.com	2	1.55

となる(それは別にしてメンテしないといけないファイルがある...)。

そんなファイルは使用してもいないし、リンクしてもいない。不思議だったので、Infoseekなどでfavicon.icoを検索してみると、他のWEBサイトのログファイル中でも同様のエラーログが生じていることはわかった。しかし、その時はそこまでしか考えなかった。その時は、favicon-> Famiconかな?というような安易な発想しかしていなかったのだ。その時に、favicon-> favorite iconと気づくべきであった。そうすれば、何が起きているかもう少し把握することができたはずだ。あるいは、納得するまで止めるべきではなかった。

　こんな反省はおいておいて、とりあえず、週間ASCII中に紹介されてた詳しい記事のリンクを追ってみることにした。

　まずは、
http://www.hotwired.co.jp/news/news/technology/story/2322.html
で概要がわかる。さらに、
http://msdn.microsoft.com/workshop/essentials/versions/ICPIE5.asp
でMicrosoftのもう少し詳しい技術紹介がされている。以下のような内容である。

　ユーザーが「お気に入り(favorites)」にあなたのサイトを登録した場合に、ユーザーが使っているブラウザーの「あなたのサイトへのリンク」の横にロゴを表示させたいと思うなら、favicon.icoという名前のファイルをあなたのドメインのrootディレクトリにおけば良い。InternetExplorerは自動的にこのファイルを探して、全てのお気に入りとクイックリンクの横にアイコンを表示させる。
　もしも、rootディレクトリにfavicon.icoを置くことができないのならば、次のようなタグをページ中に加えることで、他の場所に置くことができる。

<LINK REL="SHORTCUT ICON" href="/path/foo.ico">

また、次のようなスクリプトを使うことで、InternetExplorerのユーザーにあなたのサイトを自動的に「お気に入り」に登録するように促すリンクをつけることができる。

<SCRIPT>
<!--
if ((navigator.appVersion.indexOf("MSIE") > 0)
&& (parseInt(navigator.appVersion) >= 4)) {
document.write("<U>
<SPAN STYLE='color:blue;cursor:hand;'
onclick='window.external.
AddFavorite(location.href, document.title);'>
Add this page to your favorites</SPAN>
</U>");
}
//-->
</SCRIPT>

　そこで、実験してみることにした。まずは、favicon.icoを作成し、サーバーに置く。また、本ページのトップに
<LINK REL="SHORTCUT ICON" href="/dekirukana/favicon/favicon.ico">
を記述しておく。そして以下に「お気に入りに追加するためのリンク」を貼り付けておく。ただしMicrosoftInternetExplorerのバージョン4.0以降でないとこのスクリプトは見ることができない。
　さて、このリンクをクリックし、お気に入りに追加する実験を行ってみた。しかし、何故かアイコンは表示されなかった。これは手動で「お気に入りに追加」してみても同じである。何故か報道されているようにはならない。私がどこか間違えているのかもしれない。もう少し調べてみる必要があるだろう。

念のために書いておくが、今回のこのページ(http://www.hirax.net/dekirukana/favicon/index.html)はお気に入りには追加しないで欲しい。変なアイコンが出る、と言われても困る。ただし、文句でなくてアドバイスであれば大歓迎である。

ところで、このサイトを気に入る方がいらっしゃれば、TopPage(http://www.hirax.net/)で登録して欲しい。このTopページならば安心である。

　と、書いたがTopのページにアイコンを置いて見ることにした(1999.08.31)。前は、バーチャルドメインの設定のせいなのか、上手く動作しなかったが、現在は専用のサーバーを使用しているせいかうまく動いている。IE5以降のユーザーにしか影響は無いから特に害はないだろう。