hirax.net::inside out::05月09日

■今日のソックリさん　

　今日も朝裾野の午後取手。あーしんど。吐き気がするのがやな感じ。
　そういえば、前から誰に似てるなぁ、と思っていたけど、あの人は小泉総理にそっくりだ。もちろん、Dr.マシリトにもそっくりだ。

■風景画像からの楽曲の自動生成　

　という面白いもの。知ったのはFlowerLounge はてな版を読んで。
　ギターを弾いてみた感じでは、一番下の画像の場合が「割に良い一致を見た」という感じかな？

■学校その他の教育機関における複製　

　著作権法の第三十五条を見て下さい、とのアドバイスが。

　学校その他の教育機関（営利を目的として設置されているものを除く。）において教育を担任する者は、その授業の過程における使用に供することを目的とする場合には、必要と認められる限度において、公表された著作物を複製することができる。ただし、当該著作物の種類及び用途並びにその複製の部数及び態様に照らし著作権者の利益を不当に害することとなる場合は、この限りでない。

■オートメーションの時代 ５０年後の夢　

　ロゲルギストTとしても有名な高橋 秀俊の50年近く前の1956年に「電信電話」という雑誌に発表した文章「オートメーションの時代 ５０年後の夢」　氏が予測したコミュニケーションの未来（といっても2004年にいる我々からすればほんの再来年だが）の話。「Gmailに見るコミュニケーション論と検索技術の意味」と合わせて読むのが面白いかも。from textfile.org

■静岡科学館る・く・る　

　評判が良いようなので静岡科学館る・く・るに行ってみた。今のところ、行くのであれば平日の方が良いと思う。また、行くのであれば「科学でも何でも良いから色々遊んでみたい小さな子供」を適当に遊ばせたい親子連れか、「この手の科学館に行ったことのない人」と「この手の科学館に行ったことのある人」の二人のデートというのが適切であるような気がする。

　15歳未満は無料であるし、子供が遊ぶには面白いものは結構ある。だから、たくさんの子供でにぎわっている。その代わりに、不具合を起こしたり、動いていない展示物もチラホラ見受けられる。とはいえ、とりあえず「科学でも何でも良いから色々遊んでみたい小さな子供」を適当に遊ばせたいのであれば、（近くに住んでいるのであれば）ぜひ行ってみると良いと思う。

　もし、15歳以上の大人が行くのであれば…、「この手の科学館に行ったことのない人」には少しばかり難がある。説明文不足のせいか、その展示物が何を意図しているのかがおそらく判りにくいのではないだろうか。「ふーん、面白いのかな」で終わりそうな気がする。(何でもやってみる子供よりも好奇心が旺盛ではない大人であると)最悪の場合、展示物の動かし方・使い方が判らないかもしれない。少なくとも、それらの展示物を上手く動かすことができても「それが意味する科学」には繋がらないように思える（といっても、入場料の500円分の面白さは十分あると思う）。

　そして、「この手の科学館に行ったことのある人」にとっては、「その説明不足」は字が大きくて中身が少ない本を読んでいる気分にさせる（それでも、入場料の500円分の面白さは十分あると思うが）。「面白いな、もっと知りたいな」と思っても、それ以上の情報は全くない。例えばCalifornia Science CenterやThe Reuben H. Fleet Science Center等にあるような、小さな子供向けから大学生の専門レベルまでの判りやすい説明といったものはここにはない。小さな子供向けの説明もないし、ましてやさらに詳しい説明は全くない。

　しかし、その難の結果として良い点も一つある。「この手の科学館に行ったことのない人」と「この手の科学館に行ったことのある人」の二人のデートなら、片方が相手の専任インストラクター＆ウンチク垂れ人間になれば良いわけで、この説明無しの不親切さという障害が「デートを成功させる」ことに貢献するに違いないと思う。人気展示物だと30分以上の待ち行列ができていたりするから、そんなウンチクによる時間つぶしはきっと役に立つことだろう。そこまで計算しているのであれば、実に素晴らしい心理学の応用だと思う。

　期待が大きかった分辛口のコメントになっているかもしれないが、少なくとも日経サイエンスのタイトル「大人だましの科学館」ではないような気がする。下条信輔氏の「子供だけでなく親も楽しめ、デートコースにもなる」は実に適切だと思うが（ただし、やはり説明文は足りなすぎると思う）。

■雨の中のクローバ　

　静岡科学館る・く・る帰りの登呂遺跡で。駐車場には車が5台停まってる。駐車場の隅の雨の中のクローバを眺める。雨の中の遺跡を歩くと歩きづらくて今ひとつ。

　雨の中で過ごす弥生時代の生活はもっと辛かったのだろうな、当たり前の話だけれども。

■MyClip クリック＆Clipランキング相関グラフを生成するFlash　

　MyClip クリック＆Clipランキング相関グラフを生成するFlash。二次元散布図で各記事を眺めることができる。Web設置についてのドキュメントに関する情報等はこちらにまとめられている。

■ロックの歴史　

　ロックの予備校教師陣による「ロックの歴史＠スクールオブロック」 ELOの項のラストに書いてある「それにしてもこの項、ELPの間違いじゃないのよね？」に頷く。 from YAMDAS現更新履歴

■Gmailに見るコミュニケーション論と検索技術の意味　

　Gmailに見るコミュニケーション論と検索技術の意味.

■「みんなあの子が好きだけど、あの子が好きなの私だけ」の全称量化子　

　「郭公亭の中の人はコンピュータには卵を産まない」

■リアル・モンタージュ写真　

　フォトモンタージュ繋がりで「おこちゃまは見ちゃダメよ」の写真の遠近感の無さを利用した写真(1,2)　最近、「ミニカーの駐車」とか「掌に人を乗せる」とか「写真とリアルな人をモンタージュさせる」とか色々あるが、あんな感じのあくまで「おこちゃまは見ちゃダメよ」。

■zphoto 1.0　

　Flash ベースのフォトアルバムを作るツールzphotoのWindows バイナリもついにバージョン1.0で公開。

■フォトモンタージュのトリックを検証する　

　「和歌山県・雑賀崎沖埋立問題について」の中にある「フォトモンタージュのトリックを検証する」　ある環境問題で使用された写真に関して、写真の画角が人に与える印象等を検証している。

■漂流するカメラ　

　"A camera, alone in the world. Each Randompixel camera was given to a stranger. Stickers on the camera instruct the recipient to take a few pictures and pass it along. When the camera is done, it is dropped in the mail, it returns home, and the pictures are posted here."というRandompixel・　from 百式

■トッパン・フォームズの郵送できる「しゃべる紙」　

　トッパン・フォームズの郵送できる「しゃべる紙」.

■裾野　

■「デジタルハーフトーニングの最適化と評価手法」　

　以前、純愛で世界を描ききれをキッカケに、「最適化した純愛スクリーン」を作って頂いた阿部淑人氏による講習「デジタルハーフトーニングの最適化と評価手法」が5/20に開催されます。というわけで、感謝の気持ちと期待を込めての宣伝です。

■「人生は満員電車」　

　西原理恵子の「毎日かあさん 背脂編」を読む。人生と商いは止まらない列車、という言葉を思い出すこんな一節。

生きていくっていのは、満員電車に乗るようなものでね。その中で自分の席を見つけるということなんですよ。満員でも、まず無理矢理乗っちゃうこと。そして、降りたらダメ。乗ってさえいれば、…何でも、必ず糧になる。…電車を降りさえしなければ、少なくとも終点近くで席は空くもんだ（笑）。　　　やなせたかし×西原理恵子

■「新幹線」という名前の場所　

　「新幹線」という場所がある。静岡県函南町にあるその場所は、東海道新幹線が開業するずっと昔、第二次大戦中から「新幹線」という名前で呼ばれていた。

　昭和十年代、「新幹線（弾丸列車）計画」が進められていた。その際、新丹那トンネル工事を行うために工事宿舎が建てられていた地区が、いつしか「新幹線」と呼ばれるようになり、昭和29年には正式に字（あざ）名となった。

　「新幹線（弾丸列車）計画」の流れを汲む東海道新幹線が起工されたのが昭和34年、開業したのが東京オリンピックが開催された昭和39年だ。新幹線という名前の場所は、その場所近くを通る「新幹線」を、20年ほども待ち続けていたことになる。

　最初の「新幹線」を新幹線という場所が20年ほど待ち続けていたように、それぞれの地名はそれぞれの歴史を持っている。不思議な地名を目にすると、歴史ミステリの表紙を開く心地になる。

■「野球の統計データ」を通して眺める「統計解析の基本と仕組み」　

　山口和範「図解入門 よくわかる統計解析の基本と仕組み―統計データ分析入門 」は、わかりやすい本です。けれど、この本の読んでいて感じる面白さは「わかりやすさ」より、「心で感じることができる楽しさ」にあると思います。

　どういうことかというと、この本にに出てくる例は「現実に即した例」で、それが工場の不良品率とかいった役に立つけれど「私たちの仕事から離れた趣味」とは必ずしも繋がらないような例ではなく、「私たちの私たちの趣味」と繋がるような、「（本当に）実際の野球選手にまつわるさまざまなデータ」なのです。不思議なくらい、そんなデータで「相関」や「主成分分析」などの話題が説明されていくのです。面白い本です。

　まずは、本塁打とフォアボールの数の関係を示したグラフが下の図になります。たとえば、このデータの場合イは、「本塁打を打つ選手は（に対しては）、フォアボールが多い」という直観・実感に即したデータです。ホームランバッターにはボール球を多く投げたくなる状況が多いでしょうから、これはごく自然なデータでしょう。ちなみに、ここで言うホームランバッターというのは、本塁打数が20本を超えるような選手だということがこのグラフからわかります。

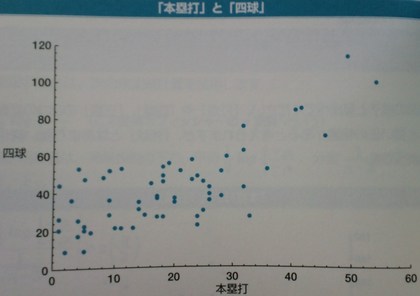
　ところが、次の「本塁打」と「死球（デッドボール）」の関係グラフを眺めてみると、少し意外に感じます。ホームランバッターには危険球ぎみのボールを投げ、その結果デッドボールが多くなるかと思いきや、そういうわけではないようです。・・・考えてみれば、死球が多く、その結果怪我をしがちだったりしたら、ホームラン（本塁打）を多く打つことができなくなってしまうわけですから、これもよくよく考えてみればあたり前なのかもしれません。

　というわけで、ここまでは、よくよく考えてみると自然に納得できるデータです。次のまだ「関係がよくわからないデータ」は、打率と三振の関係を示したデータです。高打率を誇る選手は三振が少なそうに思えるのですが、そういうわけではないようです。どういう状況があることで、こういう関係が成り立っているのでしょうか。

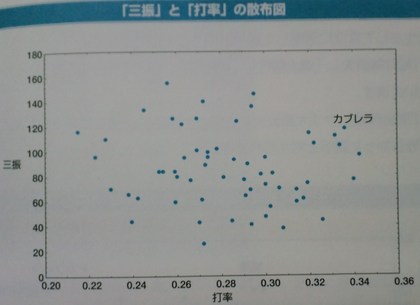
直接私たちの何かの役に立つわけでもない「野球の統計データ」を通し、私たちが直接役に立てることができる「統計解析の基本と仕組み」を学ぶのは、何だか楽しく思えます。

■Rubyで数独ソルバを書いてみる　

　「Rubyで数独ソルバを書く（が、動かない…）」のコードを見直したところ、なぜ動かなかったがわかりました。理由は簡単で、Arrayに2次元行列を格納しているときには、 "a=self.dup" というコードでは2次元行列のディープ・コピーがされない、ということでした。ごく初歩的な間違いです。

　そこで、コードを修正し、また、少しコード量を短くしてみたのが、下のRuby ソースです。関数は全部で3つ、「解答であれば出力し、そうでなければ探索をする」という関数 "find" と、1～9野数字で埋まっていない部分（すなわち、0が入っている部分）を、周りおよび該当行・列を見た上で候補を上げ、候補数値で埋めた上でさらに探索を再帰的に行う関数 "deepen"と、候補数値群を作りだす関数、"candidates"です。

require 'pp'
def find b # isGoal or serach (b=boad)
 ( !b.flatten.include?(0) && !pp(b) ) || deepen(b)
end

def deepen b
 l=b.flatten.index 0; x,y=[l%9, (l/9).floor]
 candidates(b,x,y).each{ |v| a=b.map{|c| c.dup};a[y][x]=v;find a}
end

def candidates b,x,y
 h,v=[3*(y/3).floor, 3*(x/3).floor]
 (1..9).to_a-b[y]-(0..8).map{|i| b[i][x]}-
     (h..h+2).map{|i|　(v..v+2).map{|j| b[j]}[i]}
end

find [[0,0,0,0,0,7,0,9,0],
[0,3,0,0,2,0,0,0,8],
[0,0,9,6,0,0,5,0,0],
[0,0,5,3,0,0,9,0,0],
[0,1,0,0,8,0,0,0,2],
[6,0,0,0,0,4,0,0,0],
[3,0,0,0,0,0,0,1,0],
[0,4,0,0,0,0,0,0,7],
[0,0,7,0,0,0,3,0,0]]

[[1, 2, 3, 4, 5, 7, 8, 9, 6],
 [4, 3, 1, 5, 2, 9, 6, 7, 8],
 [2, 7, 9, 6, 1, 3, 5, 8, 4],
 [7, 6, 5, 3, 4, 8, 9, 2, 1],
 [5, 1, 4, 9, 8, 6, 7, 3, 2],
 [6, 8, 2, 7, 9, 4, 1, 5, 3],
 [3, 5, 6, 8, 7, 2, 4, 1, 9],
 [9, 4, 8, 1, 3, 5, 2, 6, 7],
 [8, 9, 7, 2, 6, 1, 3, 4, 5]]
[[1, 2, 3, 4, 5, 7, 8, 9, 6],
 [4, 3, 1, 5, 2, 9, 6, 7, 8],
 [2, 7, 9, 6, 1, 3, 5, 8, 4],
 [7, 6, 5, 3, 4, 8, 9, 2, 1],
 [5, 1, 4, 9, 8, 6, 7, 3, 2],
 [6, 8, 2, 7, 9, 4, 1, 5, 3],
 [3, 9, 6, 8, 7, 2, 4, 1, 5],
 [9, 4, 8, 1, 3, 5, 2, 6, 7],
 [8, 5, 7, 2, 6, 1, 3, 4, 9]]
・
・
・

　コードは、およそ12行ほどですから、（「数独で見るRuby（と Mathematica）のパワーと表現力」の10行にはとてもかないませんが）比較的コンパクトと言えそうです。また、本来のアルゴリズムとは関係のない、2次元のArray要素を検査・操作する部分に行数を費やしてしまっているので、（そういったよく使いそうな）メソッドをArrayクラスに追加するライブラリを書きたくなります。

　それにしても、プログラムのアルゴリズム・コードを作り・書くという作業は、とびきり面白いパズルを解くのと同じ楽しさ（そして辛さ）を与えてくれます。ハマると、止められません…。

■都市化が生み出す!?「上空の風に逆らう」煙突の煙！　

　学生の可能性を可能にするポータルサイト ワンダーノーツに『都市化が生み出す!?「上空の風に逆らう」煙突の煙！』を書きました。

　「上空に浮かび流れる雲」と「煙突からモクモクとはき出される煙」が、なぜか正反対の向きへと動いているのです。

　この「（東京湾の）地上と上空の風向きの逆転現象」は、近年ますます増大している！？という研究報告があります。

■AKB48で「肌領域」を検出してみよう!?　

　Mathematicaで肌領域を検出してみる（Seeing Skin with Mathematica）という記事が面白かったので、記事で用いられていたMathematicaコードを使い、AKB48　"Baby! Baby! Baby!" の写真で「肌領域」検出をしてみました。"Baby! Baby! Baby!"の水着画像をテスト画像として使った理由は、「背景の色が肌色と近く・区別するのが難しいように見えたから」「水着はセクシーで画像処理意欲が湧くから」という２点です。

　下に並べた２枚の画像は、左が元画像で、右が肌領域を検出した結果です。背景の階段影部分を「肌領域」として抽出する「検出ミス」も生じていますが、簡単な処理の割には、比較的良い結果が得られています。

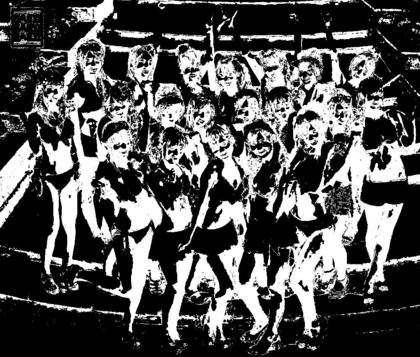
　このMathematicaコードは、学習用画像群（画像に対して肌領域を指示した教師データ）をCIE XYZ表色系で評価し、「肌色」っぽさの特徴を作ることで、肌領域抽出を行っています。教師用データには「肌色」が異なる幾通りもの人種画像も含まれていて、白人・黒人・黄色…といった辺りを変えてみても、それっぽく結果が返ってきます。

　ふと、こんなことを考えます。街中にある防犯カメラで、１年３６５日「肌領域抽出」を続けたら、「お肌の露出率」推移などを知ることができるかもしれません。そして、そんなデータを１０年、２０年集め続けたら、肌露出に対する意識変化を眺めることもできそうです。

　肌領域の検出、あなたなら、どんな楽しみ方・活用をしてみたくなるでしょうか？

■エクセル（に限らず）表示されてる値は「ホント」の値とイコールだとは限りません!?　

　Microsoft Excelでルックアップテーブル（入力値と出力値の対応表を使い、入力値から出力値を返す機能）を使いハマった方がいました。その状態を再現してみたのが、下に貼り付けた画面です。（画面右にある）「入力値Table(Index)と出力値Table(Value)を対応付ける対応表」を使い、LOOKUP関数およびVLOOKUP関数により、画面左上部にある入力値（Index）から値出力をさせてみたところです。見るとわかるように、入力値（Index）には1.8とタイプされていて、（対応表は入力・出力の組み合わせとして同じ値が入っているので）返ってくるのも1.8かと思いきや、出力されているのは1.7という結果です。･･･一体なぜなのでしょうか？　エクセルの「バグ」なのでしょうか？

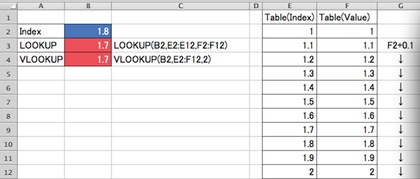
　これは、浮動小数点演算の結果によるものです。対応表は1に0.1を繰り返し足すことで作ってあるのですが、１０進法の0.1は2進法の分数で表現される浮動小数点では正確に表すことができないため、この「対応表に”1.8”と表示されている値」は、本当は1.8とイコールな値ではないのです。だから、エクセルのLOOKUP関数は1.8とイコールな箇所を見つけることができず、1.7を返すわけです。

　ちなみに、エクセルのブックオプション（計算方法）にある「表示桁数で計算する」というオプションにチェックを入れると、こうした現象は（たいていの場合は）出なくなります。なぜかというと、表示している程度に丸められてしまうため、「本当は1.8とイコールな値ではないもの」も1.8に丸められてしまうからです。

　というわけで、エクセル（に限らず）表示されてる値は「ホント」の値とイコールだとは限りません!?というのが、今日の教訓でした。･･･あるいは、単純明快で無いことをエクセルでやってはイケマセンというのが、本当の今日の教訓かもしれません。

■自転車乗りつつ投げ入れることに最適化されたような「ダンクシュート的ゴミ箱　

　自転車王国に「普通」にあって、けれどそれを意外に感じたのが、この自転車乗りつつ投げ入れることの最適化されたような「ダンクシュート的なゴミ箱。…さて問題です。自転車に乗り・（地球表面上で）手から離したゴミがこのゴミ箱が自然な軌跡で入るとしたら、自転車に乗る人たちの平均時速はおよそ何ｋｍになるでしょうか？