2000-08-24[n年前へ]
■スクール水着の秘密 
腹の部分のデカイ穴 流体力学入門編2
先日、「とあること」を知って、とてもビックリした。とてもびっくりしたあまり、「男と女の人の間には知らないことがいっぱいあって、そこには深くて暗〜い河が流れているんだなぁ。」とシミジミと考え込んでしまったくらいである。いや、誇張でなくて本当にそう思ったのである。
今回出てくる話を私のように知らない人がいたならば、もしそれが男性であれば私のようにビックリして哲学的なことを考えてしまうだろう。そして、それがもしも女性であれば「自分が常識だと思っていたささいなこと」を知った男性が「どれほど驚愕するか」を知れば、やはり同じようにビックリするに違いない。私はこの「とあることから始まる真夏の哲学をぜひ多数の人に知って頂きたい」と思い、筆をとることにした次第である。
一体、その「とあること」が何かと言うと、それは「女の子のスクール水着のお腹部分は実はセパレートになっていて、大きな穴が開いている」ということである。一応、簡単な絵を示しておこう。
 |
といっても、私が詳しく知っているわけはないので、もっと詳しいことは、
- スクール水着の謎 ( http://tako.2ch.net/test/read.cgi?bbs=entrance&key=964275735 )
- 一般的なスクール水着のしくみについてのご説明 (http://kanna.piko.ne.jp/page-L/picture.LLL.htm )
何故、そこに「スクール水着の謎」の中で、
あそこの部分は”前垂れ(まえだれ)”って言うんだよ 。あのね、あの前垂れはね、泳いでいる時に胸の谷間から入った水を泳いでいる方向から観て後方に 排出する為に有るの、あれが無いと胸の谷間から入った水が水着の中に溜まっちゃうのよ。 だから簡単に言うと前垂れは、排水口みたいな物なの。という風に簡潔に説明されている。そう言われてみれば、そういうものなのかもしれない。しかし、ビックリである。ちょっと本当に驚いて、そして少し感動までしてしまった私は「スクール水着の前垂れ部分の水流の様子」を今回解析してみることにしたのである。
まずは、こんな感じで泳いでいる女性がいたとしよう。
 |
この画像では水着が見えないかもしれないが、この女性は当然水着を着ている。「心の清らかな人」にはちゃんと水着が見えるハズである。「邪な心の人」には水着が見えないかもしれないが、それは心に煩悩を抱えているせいである。ぜひ、悔い改めて欲しいと思う。まして、「コイツPoserの使い方が判らないんだろう?」などという言うような輩(ヤカラ)はもってのほかだ。
さて、この下の画像のように女性の胸の辺りの水流を解析してみることにしよう。注目する領域はすなわち赤い線で囲んだ部分である。
 |
上の画像で胸を消してあることが判るだろう。それは今回の解析は胸の谷間から水着の中に入っていく水流の解析をする、つまり胴体の中央部での水流の解析をするからである。胴体の中央部にバストがついている女性はそうそういないだろう。
さて、その部分の拡大図を次に示そう。スクール水着に前垂れがなくて、水着の中に入った水の逃げ場がない場合、次の図のような感じで胸と水着の間にスペースができてしまう。
 |
一方、スクール水着に前垂れがあって、水着の中に入った水の逃げ場がある場合、次の図のようになる。胸と水着の間にスペースができることは同じであるが、そのスペースから水が排出されていく経路があるわけである。
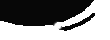 |
さて、今回の流体解析も
の時と同じく、Nast2Dを適当に改造して簡単に解析を行ってみた。今回はReynolds数は100で計算してみたが、次に計算するときにはReynolds数の妥当な値を考慮してやってみたいと思う。残念ながら、今回は本当に適当に計算をしてみただけである。まぁ、最初の試しだからそんなものだ。 まずは「前垂れがなくて、水着の中に入った水の逃げ場がない場合」の水流の速度分布の計算結果を下に示してみよう。
 |
胸の谷間に水がたまったスペースの後ろ部分の水流がずいぶんと速くなっていることがわかるだろう。当然のごとく、胸の谷間に水がたまった部分では水は滞留してしまっている。
一方、「前垂れがあって、水着の中に入った水の逃げ場がある場合」が次の図である。
 |
胸の谷間を水がジェット気流のように速く抜けていくことがわかる。割にどの領域でも、水流の速度分布は割に等しくなっている。
次に圧力分布と水流の速度分布を重ねてみたものを示してみよう。まずは、「前垂れがなくて、水着の中に入った水の逃げ場がない場合」である。
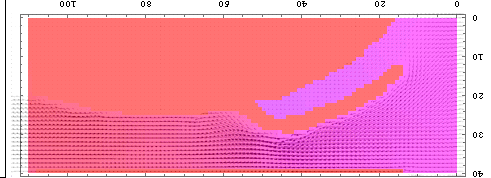 |
胸の谷間に水がたまっている部分は圧力が高いが、その外側の部分は圧力が低くなっていることがわかるだろう。
この圧力差により、次の図のような力が働いてしまう。
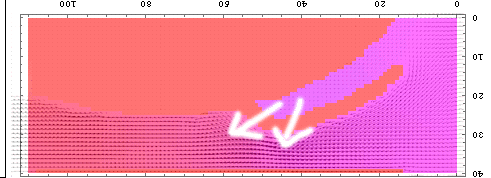 |
こんな力が働いてしまうと、速く泳ぐ邪魔にもなってしまう。また、この力が大きくなると水着の締め付ける力を上回ってしまうだろうから、ますます水がたまるスペースが大きくなったり(つまり胸のスペースが広がってしまったり)、さらには水着を脱がす方向に働いてしまうことだろう(それはそれで良いぞ、という声も聞こえてきそうであるが)。
一方、「前垂れがあって、水着の中に入った水の逃げ場がある場合」は次の図のような感じである。
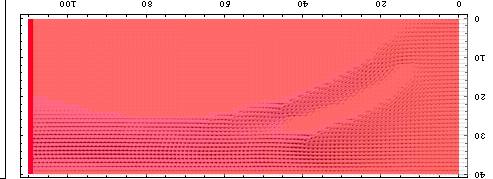 |
圧力の不均衡もそんなに発生していないことが判るだろう。これなら速く泳ぐ邪魔にもならないし、水着もちゃんと体にフィットしたままである。
このように、スクール水着に隠された「前垂れ」は実に役に立っていることが流体解析からも判るわけだ。いやぁ、本当にビックリだ。
さて、私の周りの男性はやはりみな「スクール水着の秘密=前垂れ」を知らなかった。
「腹の部分にデカイ穴〜!? はぁ? スクール水着にそんなものあるわけないじゃないの。」とみな口を揃えて言うのである。もう、誰一人として素直に信じる人はいないのである。しかもこともあろうに、私をヘンタイ扱いまでするのである。いつの時代も真実を伝える者は受難の運命が待っているのである。実に嘆かわしいことである。
「オマエ、変な妄想でも見たんじゃないの〜」
しかし、それが「スクール水着の真実」を知ってしまった後は、どの人も
「えぇ〜!! 昔の俺達にそれを教えてやりたい〜!!」と驚きのあまり興奮してしまうのである。しかも、みんな
「誰一人としてそんなこと教えてくれなかったぞぉ〜」
「俺達の青春を返せ!って気分になるなぁ〜」
「もっと早く教えてくれよぉ〜」というニュアンスがアリアリと感じられるのである。さっきまで人をヘンタイ扱いしていたくせに、コロッと変わりすぎである。
しかし、女性陣はと言えば、
「あぁ〜そう言えば、そんな風になってたような〜。」と実に淡々としたものなのである。男心を全然判っていないのだ。その証拠に、
「あそこの穴から空気を入れて遊んだ〜。」
「えぇ〜、知らないのぉ〜」
「それにしても、何でそんなに驚くのか全然判りませ〜ん。」と言う人までいるのである。「そりゃ、驚くぞ」と男なら判るはずなのだが、それが女性にはどうも伝わらないのだ。
そういうわけで、「スクール水着の秘密」を通して私は「男と女の間の常識・意識のギャップ」を本当に真剣に考えさせられたのである。そのショックの余韻は今もまだ醒めやらぬままだが、とりあえず今回はここまでで終わりにしたい。
2000-10-29[n年前へ]
■「しょんべん小僧」の物理学 
あともう一歩、前に出ろ
以前、- スクール水着の秘密 - 腹の部分のデカイ穴 流体力学入門編2 - (2000.08.24)
「男性にはよくある風景だけれど、女性にとっては未知のミステリアスゾーン」といってもたくさんあると思うが「男子トイレ」というものだって、女性にとっては未知のミステリアスゾーンだろう。
次の絵はよくある男子トイレの一風景だ。便器前のポジションに立つとどうしても目に入る位置にこんな内容を書いたチラシが張ってあることが多い。
「ちょっと待て、あともう一歩前に出ろ。」
 |
もし、その張り紙がなかった場合にはどうなるだろうか?その場合には、下の絵のような事故が発生してしまうのである。実際のところ、ほとんどの公衆便所で見かける風景だ。
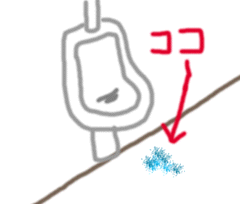 |
そう、便器にロックオンして放水をしたハズなのに、何故かターゲットである便器まで「小便」が届かずに便器下を汚してしまうのである。実にマズイ事態ではあるがよく見かける風景でもある。便器内を狙ったハズの小便が残念ながら目標地点まで辿り着かなかった場合に起きる悲劇である。
もちろん、どんなに飛距離が小さくても、すなわち小便が放水銃の先から真下に垂れてしまった場合でも、便器の顎の上から放水作業を行っていれば何の問題もないわけだ。しかし、世の中の男性達は何故か遠くから狙いたがるのである。先程の、「ちょっと待て、あともう一歩前に出ろ。」という張り紙ではないが、もう一歩前に出て便器の顎の上から放水作業を行いさえすれば良いのではあるが、何故か漢(ここではあえて、漢と書いてオトコと読むことにしよう)達はそれができないのである。
さて、この現象には別に公衆便所でなくても発生するわけで、どこのトイレでも便器の下を汚してしまうことになる。そのため、家庭によっては妻から
はるか古の昔から「男らしさ」のひとつが「立ち小便」でなかったか?、そして「立ち小便」は「男らしさ」の最後の砦ではないのか?という気も私は少しだけしたりするのだが、便器周りを汚しまくる現実の前ではそんな「男らしさ」は2000円札よりも価値がないのである。2000円札ならば喜んで受け取ってくれる人もいるだろうが、便器の下に落ちようとする「小便」は誰も受け取ってくれない。いや、実際のところ小便を喜んで受け取ってくれる人もいるのかもしれないが、少なくともそんな人の数は2000円札を喜んで受け取る人の数よりはきっと少ないだろうと思うのである。
そしてさらに、「男らしさ」が「立ち小便」なら、そんなものイラナイと言われてしまいそうな気もするし、「立ち小便」が「男らしさ」の最後の砦か!?と言われてしまいそうな気も強くするので、ここらへんについての社会学的な考察は追求しないでおこう。
それでも、私は世の中の虐げられている「しょんべん小僧」達のため、そして「男らしさ」の最後の砦を守るために、男子トイレの「しょんべん小僧」達がどうしたら、放水ミスをしないかを物理的に考えてみることにしたい、と思うのである。
さて、便器まで小便が届かないという「放水ミス」はどのようにすれば防ぐことができるだろうか?小便の飛距離を小さくしないためにはどのようにしたら良いだろうか?そのためには、まず小便の飛距離がどのようにして決まるのかを考えなければならないだろう。
下のちょっとリアルな「しょんべん小僧」の放水作業ではないが、小便の軌跡はきれいな放物線を描く。
 |
すなわち、空気抵抗などは無視した場合のピストルの弾と同じく
- 銃筒の先端を出るときの初速度
- 銃筒の角度
銃筒の先端を出るときの初速度 = V0と表すと、小便の飛距離は
銃筒の角度 =θ
a V0^2 Sin[2θ] (aは定数)と表される。この式を見ればθ = 1/2 rad.の時にSin[2θ]が1になるので一目瞭然であるし、また感覚的にも自然であるが、銃筒の角度の方は上向き45度の角度に向けるときに小便の飛距離は最大になる。一方、初速度V0の方は速ければ速いほど、小便の飛距離は伸びる。
それを示したのが、次の図である。「小便の銃筒の先端を出るときの初速度と銃筒の角度を変えた時の小便の飛距離」を示したものだ。
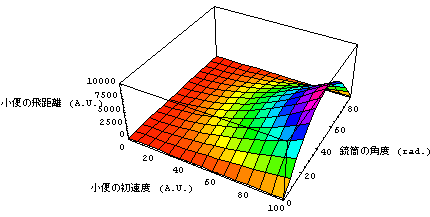 |
すると、便器まで小便が届かないという「放水ミス」すなわち、小便の飛距離を小さくしないためには、銃筒の角度を大きくしすぎたり、小さくしすぎたりしないという知見が得られるわけであるが、そんなことは当たり前だ。誰もトイレで銃筒を真上に向けたり、真下に向けたりはしないのである。先のちょっとリアルな「しょんべん小僧」ではないが、手で放水銃を支持している限り何の問題も無いのである。
つまり、便器まで小便が届かないという「放水ミス」はほとんどの場合「放水銃の角度」のせいではないのである。つまり、「銃筒の先端を出るときの初速度」が問題だったと考えるのが自然である。
それでは、「銃筒の先端を出るときの初速度」はどのようにして決まっているのだろうか?それを大雑把に考えてみたのが次の図である。腹筋で膀胱に圧力Pをかけて、銃筒の先端から小便を初速度V0で放水作業を行うのである。
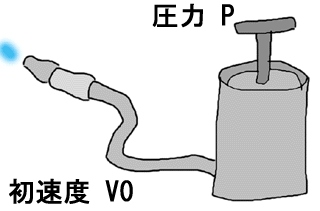 |
ところで、上の絵でポンプとして表した膀胱に圧力Pをかけた場合には、膀胱からb P (bは比例定数)と表せる量の小便が銃筒に送り込まれるものとしよう。その場合、その量の小便が銃筒の先端から単位時間に出るわけであるから、銃筒の先端の口径をAとすれば、
V0 = b P /Aと表すことができる。すなわち、「銃筒の先端を出るときの初速度V0」は腹筋で膀胱を締め付ける圧力Pに比例し、銃筒の先端の口径Aに反比例するのである。
さて、いくら腹筋が強い人であっても腹筋をいきなり締め付けることはできない。つまり、腹筋で膀胱を締め付ける圧力Pというものは徐々に大きくなるのである。
すると一見、「銃筒の先端を出るときの初速度V0」も0から徐々に大きくなる、すなわち、放水作業を開始した最初の瞬間は「銃筒の先端を出るときの初速度V0」= 0であって、小便の飛距離も0である、つまり、便器まで小便が届かないという「放水ミス」が必ず起きるかというと、実はそういうわけではない。
ポンプである膀胱から銃筒の先端までは、ある程度の長さがある。もちろん、その長さは一定ではないのだが、とにかくある程度の長さがある。そのため、小便が銃筒の先端から出る瞬間には、ポンプである膀胱にかかっている圧力Pは0ではないのである。すなわち、膀胱から銃筒の先端まである程度の長さがありさえすれば、「銃筒の先端を出るときの初速度V0」は結構大きくすることができるのだ。もちろん、腹筋を鍛えて、腹筋に急激に力を掛けることができれば、その効果はさらに上がることは言うまでもない。
だとしたら、一般的に便器まで小便が届かないという「放水ミス」は一体何時起きるのであろうか?それは、「銃筒の先端を出るときの初速度V0」を決める膀胱にかかる圧力Pが低下し、なおかつ最初の瞬間と違い「膀胱から銃筒の先端までの長さ」を有効に活用できない、放水作業を終える瞬間である。飛行機でも着陸が一番難しいというが、この放水作業もやはり放水作業を終える瞬間が一番難しいのである。そのため、多くの場合小便達は便器内への着陸に失敗し、便器の下を汚してしまうのである。
しかし、私は「男らしさ」の記念物でもある「立ちしょうべん」を守るために、一つの解決策を考えついたのである。「男らしさ」の最後の砦を守る技術を提唱したいのである。すなわち、「銃筒の先端を出るときの初速度V0」は腹筋で膀胱を締め付ける圧力Pに比例し、銃筒の先端の口径Aに反比例するのであるから、放水作業のラストに膀胱を締め付ける圧力Pが小さくなった、あるいは、膀胱を締め付ける圧力Pを有効に膀胱からの排水に変換できない排水作業のラストにおいて、銃筒の先端の口径Aを小さくしてやればよいのである。そうすれば、「銃筒の先端を出るときの初速度V0」は「銃筒の先端の口径A」に反比例するのであるから、膀胱から出てくる小便の量が低下しても、「銃筒の先端を出るときの初速度V0」を0にならないように維持することができるのである。これにより、放水ミスを防ぐことができるハズなのである。
さて、私は「男らしさ」の最後の砦である「立ちしょうべん」を守るために、このような技術を考えてみたわけであるが、この技術の実証作業は行っていない。果たして、「銃筒の先端の口径A」を自分の意識で小さくすることができるか!?というところに大きな問題点があるような気もするのであるが、それは「男の意地」で克服できると私は信じている。外部から制御するって手もあるのだし。って何の手の話だ、全く。
2001-01-23[n年前へ]
■今日の疑問 
次回の話は流体力学の話なのだが、某サイトでも同じく流体力学の話が出ていた。なかなかに面白い。ところで、粘性項を無視したポテンシャル流れで、最短距離の出口以外の所に先に着くのはちょっと不思議なのですけど、いかがなものでしょう? > webmaster殿
2001-01-27[n年前へ]
■オッパイ星人の力学 仏の手にも煩悩編 
時速60kmの風はおっぱいと同じ感触か?
本サイトhirax.netは「実験サイト」というジャンルに分類されることが多いようである。何が実験で、何が実験でないのかは私にはよくわからないのだが、とにかく「実験サイト」と呼ばれるサイトは数多くある。そして、その数ある実験サイトの中でも、人間そして愛について日夜取り組んでいるサイトの一つが「性と愛研究所」である。その「性と愛研究所」を読んでいると興味深いことが書いてあった。テレビ番組の「めちゃめちゃイケてる!」の中で何でも「時速60キロの風圧はおっぱいの感触である」と言っていたらしい。そしてまた、「性と愛研究所」では「おっぱいの感触と風圧に関する考察」の中で、「時速60kmでは全然おっぱいの感触ではなくて、ちょうど時速100kmを境に急におっぱいの感触を感じます。」というメールを紹介しながら、
「時速100kmの風では、本物は触れないけどお手軽に疑似体験、名付けて『プリンに醤油でウニ』ではなくなってしまう。それでは、まるで『キャビアにフォアグラでトリュフの味』だ。青少年のために疑似おっぱいを探してあげる必要があるな。」と結論づけている。
この「時速60kmの風」現象は「できるかな?」的にとても興味深いと思われるので、今回じっくりと考えてみることにしてみた。そして、この結論に何らかのプラスαをしてみたいと思う。
そう、前回「オッパイ星人の力学 第四回- バスト曲線方程式 編- (2001.01.13)」でオッパイの表面で働いている力について考えてみたのは、実は単に今回・そしてさらに次回の話のための準備だったのである。(さて、ちなみに今回は会話文体をメインに話が進む。「性と愛研究所」ではないが、この手の話は会話文体の方が書きやすいように思うし、私のバイブル「物理の散歩道」でも「困ったときの会話文体」と言われていたので挑戦してみた次第である。言うまでもないが、AもBも私が書いてはいるが、私自身ではない。)
A : 「東名高速で出勤途中に確認してみたんだが、やはり時速100kmあたりが妥当な感じだったな。」
B : 「何を根拠に妥当なのかがよくわからないが、確かに時速60kmでは手に何かが触っているという感触すらないな。それにしても、哀しい出勤の景色だぞ、それ。」A : 「ほっとけ!だけど、少し考えてみると、このおっぱい(ニセモノ)の感触問題は結構面白く、技術的にもなかなかに深い話だと思うんだよ。」
B : 「はぁそうですか…、としか言いようがないな。」A : 「まぁ、聞け。何しろこのおっぱい(ニセモノ)の感触問題には流体力学のエッセンスがぎっしりと詰まっているんだからな。」
B : 「そんな話は聞いたことはないが、とりあえず聞かせてもらおうか。」A : 「このおっぱい(ニセモノ)の感触問題を解くためには、とりあえず車の窓から手を出したときの指の周りの空気流を計算すれば良いわけだ。」
B : 「ちょっと待て。何で指の周りなんだ。手のひらじゃなくて?」A : 「簡単なことさ。試しにおっぱいを揉む仕草をしてみろよ。」
B : 「こ、こうか?あぁっ?手のひらじゃなくて指で揉んでるっ!」A : 「そうだろ。何故かわからないが、おっぱいを揉む仕草=Mr.マリックが超魔術をかける時のような指使いらしいんだよ。」
B : 「うむ、確かにそのようだな。」A : 「だから、時速60kmの風からおっぱいの感触を受けているのは指先だと考えるのが自然だろ。それなら、とりあえず下の図のような「指の間を抜けていく空気の流れ」を計算してみれば、おっぱい(ニセモノ)の感触問題が解けるわけだ。」
B : 「実写の手に二次元の計算結果を三次元的に合成するという凝った処理が、実にクダラナイことに使われている例だな…」
 | 高速で走る車の窓から手を出して、その手の指の間を抜けていく空気の流れを計算しよう。 鉛直方向の指の等方性を考えて、右の図に示すような指を輪切りにするような水平面のみを考える。 こんな写真を撮るときに、自己嫌悪に陥りがちなのは何故だか知りたい今日この頃。 |
A : 「こういう「空気の流れ」ような流体の力学は、ニュートンのプリンキピアに始まり、オイラーとベルヌーイにより非圧縮・非粘性の理想流体の運動方程式とエネルギー保存則が導かれた。それがオイラーの運動方程式とベルヌーイの式だ。オイラーの運動方程式はちなみにこんな感じだ。」
加速度 = 外力 + 圧力勾配力 v : 速度 |
A : 「基本的には「加速度 = 外力 + 圧力勾配力」という形だな。この非圧縮・非粘性の理想流体の場合はラプラシアンがゼロのポテンシャル流れと呼ばれる単純な流れになる。試しに、そんな場合をNast2Dを元にしたプログラムで計算してみた結果はこんな感じになる。ホントはこの計算自体は完全な理想流体ではないのだが、まぁ大体はこんな感じだ。」
B : 「おっ、あっという間に計算したな。」A : 「まぁ、ポテンシャル流れならエクセルでもちょちょいと計算できるくらいだからな。ちなみに、これは窓から手を出してしばらくしてからの空気の流れだ。」
 |
A : 「で、どうだ?」
B : 「いや、どうだ、と言われても困るが、なんかキレイだな。だけどちょっと小さくて見にくいなぁ。」A : 「そう言われれば確かにそうだ。じゃぁ拡大してみるか。」
 |
B : 「で、この結果から何がわかるんだ?」A : 「この図で空気は左から右へ流れているわけだが、左端の空気の速度と右端の空気の速度は、実は同じなんだ。」
B : 「そう言われても、よくわからないが?」A : 「指を通り過ぎてく空気は、指をとおる前後で運動量がそのまま変わってないってことさ。つまり、空気は指を通り過ぎる時になんら抵抗を受けてないってことだ。」
B : 「えっ?おかしいじゃないか、それなら逆に言えば指も空気から何の抵抗を受けないってことか?」A : 「そういうことだ。これがダランベールのパラドックスだ。」
B : 「じゃぁ、何か?この指先に感じるまぎれもないおっぱいの感触は幻だとでもいうのか!? そんなのオレは認めないぞ!」A : 「まぎれもない、っていうほどのものでもないし、ニセモノおっぱい自体は何か一種の幻のような気もするが、もちろん感触自体は幻であるハズはない。そもそも、空気をサラサラな理想流体として取り扱ったところが間違っているわけだ。そこで、登場するのがナヴィエとストークスだ。彼らはオイラーの運動方程式に粘性を導入した。全てはおっぱいの感触を説明するために、だ。」
B : 「それウソだろ。ナヴィエとストークスが聞いたら怒るぞ。」
加速度 = 外力 + 圧力勾配力 + 粘性力 v : 速度 |
A : 「見ればすぐわかるだろうが、この非圧縮流体に対するナヴィエ・ストークスの方程式は、最後に粘性項が入っている以外はオイラーの運動方程式と全く同じだ。」
B : 「なるほど。こうしてみると意外に簡単な式だな。」A : 「あぁ、オイラーの運動方程式に粘性項が入っただけだからな。そのせいで計算はちょっと複雑になるが、最近のパソコンならノープロブレムだ。というわけで、粘性を考慮して計算してみた結果が次の図だ。」
 |
B : 「おっ、ちょっと様子が違うな。何か、ジェットエンジンみたいに尾を引いてるぞ。」A : 「そうだろ。指の後ろのl様子がずいぶんと違うだろう。で、これを拡大してみたのが次の図だ。」
 |
B : 「左端の空気の速度はもちろんさっきと同じだが、指の後ろでは空気が渦巻いているし、右端の空気の速度は全然違うな。」A : 「もっとリアルに、窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみた計算結果のアニメーションが次の図だ。指の周りに空気が渦巻いていく様子がよくわかるハズだ。」
 | 窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみたもの。指の周りに空気が渦巻いていく様子がよくわかる。 メッシュを細かく切ったおかげで、計算結果は1GB弱。なんてこったい。 |
B : 「指が空気の中を走り抜いていく様子がよくわかるな。確かにこれなら、空気の抵抗を受けまくりだな。」A : 「そうだ。空気は指から力を受けるし、逆に、指は空気からしっかりと力を受けるわけだ。」
B : 「なるほど、この計算結果は指先に感じるまぎれもないおっぱいの感触を説明しているわけだな。いい感じじゃないか。流体力学そして粘性項さまさまじゃないか!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「おやっ?ちょっと待てよ!これでは、ただ現実を説明してみただけで、何の解決にもなってないぞ!時速60kmと時速100kmの風の感触の差を説明しているわけでもないし、青少年のためのもっと安全な擬似おっぱいを提供しているわけでもない!」A : 「いや、それがそういうわけでもない。実はこの先があるんだ。このナヴィエ・ストークスの方程式の解はレイノルズ数という無次元数によって決定されるんだ。今回の場合で言うと、レイノルズ数は「指の直径x 車の速度 / 流体の運動粘性率」という形になる。そして、このレイノルズ数が大きくなるほど渦が延びていくんだ。」
B : 「なるほど、わかってきたぞ。つまりあれだな。時速60kmから時速100kmに速度を上げれば、それに応じてレイノルズ数が大きくなって、空気の渦もおおきくなるし、おっぱいの感触も確実なものになるわけだな。勉強になるな。」A : 「う〜ん、実際には密度の違いの方が大きいんだが、ナヴィエ・ストークスの方程式の理解としてはそれでいいかもな。あと、単にレイノルズ数を大きくしたかったら指を太くする、っていうのでもいいわけだ。」
B : 「そう言われても指の太さはなかなか変えられないしなぁ。」A : 「指サックとか色々手はあると思うが、もっといい方法がある。さっきの式を眺めてみれば流体の運動粘性率が小さくなれば、レイノルズ数は大きくなる。例えば、水の運動粘性率は空気のそれの十五分の一だ。」
B : 「ってことは、水の中だったら、レイノルズ数も大きいし、密度も大きいし、指先に抵抗を受けまくりってことだな。すると、水中で手を動かしてみれば、それは空気中の高速クルージングと同じってことになるな!」A : 「そうさ、風呂の中で手をひとかきすれば良いだけの話さ。何もわざわざ時速100kmの車の窓から手を出す必要はないんだ。実際、風呂の中で確かめてみたけど、なかなかイイ感じだ!」
B : 「時速100kmで走る車の窓から手を出すのに較べれば、風呂の中で手をひとかきすれば良いだけなんて、まさに青少年のためのもっと安全な擬似おっぱいだな!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「それはもういいっ言ってるだろ。」A : 「ところで、ふと考えてみたことがあるんだ。さっき、指を太くすれば遅い速度でもレイノルズ数が大きくなるって言っただろ。東大寺の大仏なんかかなり指が太いじゃないか。」
B : 「確かに、そうだな。」
A : 「今調べてみると、大仏の掌の長さは256cmだ。つまり普通の人間の10倍くらいある。だったら、指の太さも10倍はあるだろう。ってことは、ほんのそよ風が吹いただけでも、大仏の手にはしっかりとしたおっぱいの感触が感じられているんじゃないのかな?」
B : 「単に手が大きいから空気の抵抗も大きいだけどいう気がしないでもないが、指の長さもでかいしさぞかし超巨乳の感触かもしれんな!そう考えると、あの大仏の手も何か実にイヤラシイ手つきに見えてくるから不思議だな!」A : 「う〜ん、悟りを開いているから、指先のヘンな感触なんかには惑わされないんだとは思うけどな。しかし、案外と仏もそんな煩悩と日夜闘っていたりするのかもしれないなぁ。しかも、その煩悩がホントーにあるのかもよくわからない幻のような擬似おっぱいってところが面白くないか?大仏の指先は二十一世紀の煩悩そのものを暗示しているのかもしれん。仏の手にも煩悩ってところだな!」
B : 「言いたい放題だな、全く。」
さて、今回は「オッパイ星人の力学第四回 - バスト曲線方程式 編- (2001.01.13)」と繋がるところまで話が辿り着かなかった。おっぱいの表面張力、マボロシのような指先の流体力学、そして大仏の煩悩をめぐる大河ドラマは人生そのもののようにまだまだ続くのである。
2001-04-07[n年前へ]
■スカートの力学 予習編 
風に吹かれるスカートは
四月になって、春風が強く吹き始めた。春風と言えば聞こえは良いけれど、コンタクトレンズを使っていたりする人は強い風が吹くとゴミが入ったりしやすくて辛いだろうし、まして花粉症だったりすると涙が止まらなかったりしてきっと辛いことだろう。そんな辛い季節でも、たまにドキドキするような気持ちになる瞬間がある。もちろん、それは春風にスカートが舞い上がった瞬間だ。スカートが風に吹かれた瞬間に、私は理由もなく(いや理由はちゃんとあるのだが)心と体がドキドキする。それはもちろん私だけでなくて、男なら間違いなく誰しもがそんなドキドキを味わったことがあるはずだ。もっとも、そんな男心を理解しないヤカラはそんなドキドキを軽蔑するに違いないのだが、それが男というものなのだからしょうがないのである。
とはいえ、男心は「男の心」という位だから、女性にはなかなか判りづらいことだろう。「女子高生なんかはどうせスカートの下に短パンを履いているのに、それでもドキドキするものなの?」などと言う女性も多い。しかし、「それでもドキドキしたりする」ものなのである。いや、もちろんスカートの下にジャージを履いてるなんてもっての他ではあるが、短パンくらいならドキドキ度は全然減らないものなのである。それが、つまりは男というものなのだ。
そして、逆に「スクール水着の秘密」ではないが、女性には常識でも我々男には全然判らないことが世の中にはたくさんあるに違いない。ちなみに、私にとってはスカートもその一つである。何しろ、あまりスカートについて自分のこととして考える機会がなかったのである。いや、実際のところそんな機会は全然無かったのである。そこで、今回は「春風に吹かれるスカート」について考えてみることにした。(本題に入る前に一応書いて置くけれど、今回も「スクール水着の秘密」と同じく、女性から見たら「なんて当たり前のことを」とか「それちょっと違うんじゃないの」ということを書いている。そんな風に感じた方は是非、メールででも私に情報でも頂けたら、と思う次第である。)
| さて、本題である。 この右の図のような「風に吹かれながら女性がスカートを押さえている風景」をよく見かける。もっとも、「よく」見かけるなんていうと、私がさぞそういう風景を探し求めているように聞こえるかもしれないが、そんなことはない。風が強い季節であれば、そんな風景は満ちあふれているのである。 さて、この女性のスカートのように風に吹かれたスカートについてちょっと考えてみよう。
| 女性がスカートを押さえている風景」 (animeBODY)  |
まずは、体の前方から強い風が吹いているものとする。つまり、強い向かい風が吹いている状態である。ちょっとその女性にとってはツライ状態である。そこで、うすみどり色のスカートを履いている女性は、スカートがめくれ上がらないように、スカートの前部を両手で膝近くで押さえているわけだ。しかし、それでも風に吹かれてスカートの後ろは舞い上がってしまう。例えば、下の右図で女子高生の体の後ろでスカートがめくれ上がっている。それをもっと単純にしたのが左で、この図中ではスカートはCの位置まで上がってしまっている。
 |  M.H.Tさん画 |
もちろん、男心からすればCどころではなくて、Aくらいまでスカートには高く高く舞い上がって欲しいわけであるが、女心からすればそれはとんでもない話だろう。
さて、このスカートのめくれあがる位置Cは何で決まるだろうか?もちろん、流体力学・弾塑性体力学などを総動員して解かなければならないわけではあるが、それは次回以降のお楽しみということにしておいて、予習編の今回は単純にスカートがOC方向には曲がらないものとしてみよう。だとしたら、話は簡単だ。ただスカートの裾の広さでCBの長さは制限されるわけである。スカートの裾が広ければ、スカートの端は高くまでめくれあがってしまうし、スカートの裾が狭くなっていれば、スカートは比較的低いところまでしかめくれない。
だから、この下の色々なスカートの中でプリーツ・スカートのようなフレアタイプの場合は、スカートは高隈でめくれ上がってしまうだろうし、タイトスカートのようなスカートの裾が狭いものであれば、強い風にも負けず、スカートはめくれ上がることはないだろう。
プリーツ・スカート
|
|
|
|
しかし、しかしである、スカートの裾を狭くすれば春風にスカートが舞い上がってしまうことはなくなるかもしれない。だけど、スカートの裾の長さが制限するのはスカート自身だけでない。スカートを履いている女性の動き自体も制限してしまうのである。それではずいぶんと窮屈になってしまうことだろう。スカートの裾が狭いせいで歩幅も狭くなって、走り回ったりすることもできなくなるに違いない。だからこそ、脚を蹴り上げる藤原紀香のJ-PHONECMのスカートも、脚の動きが制限されないように、スカートの後ろに切れ目が入っているのだろう。
ということは自由に駆け回ったりしようとすると、つまり、スカートが足枷にならないような裾の広いスカートを履いていると、そんなスカートは風に吹かれて舞い上がりやすいわけだ。そして、そんなスカートを履いていると春風に困らせられることになる。
とはいえ、実際にスカートを履いたことがあるわけじゃないから、私には実際のところよく判らない。だから、女性の方々の「本当はこうなのだ」という教えでも請うしかないのである。結局、スカートの話は、スカートを履く人には常識きわまりない話だろうが、私はこれまで考えたこともなかったので全然よくわからない。これが、男と女の常識の違いなのかもしれない。いや、単に私の常識知らず、という可能性が一番大ではあるのだけれど…
そういえば、辞書でskirtを引いてみると「女;女の子」なんていう風にも書いてあった。なるほど、風に吹かれるスカートも走り回るスカートも、確かにその女性そのものなのかもしれないなぁ、と少しばかり思ったりしたのである。だとしたら、風に吹かれるスカートは向かい風には負けないで欲しいな、と柄にもなく思ってみたりするのである。ホントに私の柄じゃないのだけれど。




