1999-12-21[n年前へ]
■恋の力学 
恋の無限摂動
クリスマスが近くなると、街のイルミネーションが綺麗に輝き始める。いかにも、ラブストーリーが似合う季節である。そこで、今回は、"Powerof love"、すなわち、「恋の力」について考えてみたいと思う。「恋の力」により、人がどのような力を受け、人がどう束縛されるのか、などについて考えみたいのである。また、恋に落ちたカップルがどのような行動をするのかについて解析を行ってみたい。
「できるかな?」では以前、
において、カップルが他のカップルを意識する力について考えたことがある。カップル同士の間に働く斥力を考えることにより、鴨川カップルの行動を考えてみた。それと同様に、今回はひとつのカップルのみを考え、その中に働く力を考えてみるのである。ひとつのカップルの「男」と「女」の間にどのような力が働くかを考えるのである。そういうわけで、今回の登場人物は「男」と「女」である。その二人は「恋に落ちた二人」である。二人の間には「恋の力」が働いているのだ。その二人の間に働く「恋の力」について考察することにより、恋に落ちたカップルの行動について考察を行ってみることにする。
といっても、「恋の力」を精密に測定した報告例は未だ存在しないので、ここでは適当な値を用いていくことにする。「恋は距離に負けない」とか「遠くて近きは男女の仲」などとははよく言われる。そこで、距離によらないと近似した。また、「遠くて近きは男女の仲」の意味を考えれば、恋の力は無限遠まで働く力である、と考えるのが自然である。
そこで、今回の「恋の力」は距離に関わらず一定であると仮定した。距離=rとした時に-r/Abs[r]の大きさで「相手に惹かれる」ものとした。仮に第一種「恋の力」(仮称)とでもしておく。
今回は「恋の力」は距離によらないものとした。しかし実際は、(通所の距離においては)「男」と「女」は距離が近いほど惹かれ合うし、離れてしまうと惹かれ合う力は弱くなるというのが自然であると思われる。そこで今回の第一種「恋の力」(仮称)は、あくまで大雑把な近似ということにしておく。
恋する二人の間に働く力をもう少し正確に記述しておくと、
- 「恋の力」 = - 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「恋の力」=優柔不断度 * 「恋の加速度」
であることだ。心がトキメいてもなかなか行動を起こすことが出来ない人がいるだろう。そういう人は「優柔不断度」が高いというわけである。恋の行動における慣性を示すパラメータである。
また、今回は空間を1次元であると簡略化してみた。1次元の空間の中で「男」と「女」が動き回るのである。その時間的変化を調べてみるのだ。従って、シミュレーション結果は空間軸が一次元+時間軸一次元で、合わせて2次元となる。
さて、この「恋の運動方程式」を解くことにより、恋する二人の行動は予測することが可能となるわけだ。試しに、その計算サンプルを示してみる。なお、今回は時間方向で数値的に逐次解を求めている。
初期状態は
- 「男」位置=5, 速度=0,魅力=100,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
位置や時間の単位は任意単位である。「0」と「5」は東京と大阪であっても良いし、ロンドンとニューヨークであっても良い。あるいは、実空間でなく精神的な空間と考えてもらっても構わない。すなわち、心の動きを示しているものとするのである。
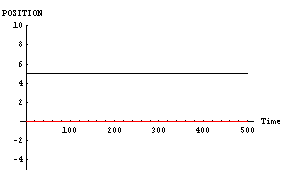
また、二人の「魅力」や「優柔不断度」は対等である場合だ。その結果を下に示す。このグラフは縦軸が空間位置であり、横軸が時間である。黒線が「男」であり、赤線が「女」である。
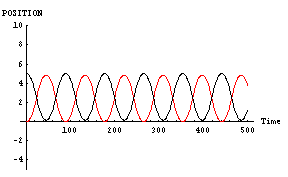 |
「男」と「女」が同じように相手の方向へ向かっているのがわかると思う。これが「恋の無限摂動」である。こういった「恋の無限摂動」の代表的なものには「君の名は」の主人公達の動きなどがある。恋に落ちた二人が、延々とすれ違いを続ける物語である。これは、この「男」と「女」の行動そのものである。
この計算結果では「男」と「女」が糸を紡いでいるようにうまく絡みあっているのがわかる。「恋の無限摂動」の幸せなパターン例である。これは、「男」と「女」が対等であったことがその一因である。
その証拠に、「男」と「女」が対等でない場合の計算結果を示してみる。次に示すのは、
- 「男」位置=5, 速度=0,魅力=10,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
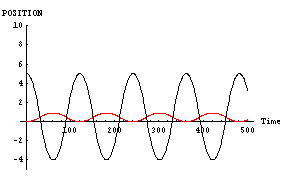 |
「男」が右往左往するのに対して、「女」はほとんど動いていないのがわかると思う。おそらく、この場合には「男」と「女」の「心」もこれと同様のパターンを示しているものと思われる。すなわち、「男」の「心」は揺れ動いているのに対し、「女」の「心」はほとんど動いていないのである。
先の例と異なり、これは実に不幸な計算例である。不幸ではあるが実際によくある例であると思う。以降、これを「男はつらいよ」パターンと呼ぶことにする。「女」に「男」が振り回されているパターンだ。もし、奇跡的に結婚などしても、将来どうなるかは火を見るより明らかである。
それでは、「男」と「女」の「魅力」が同等で、かつ、とてもスゴイ場合を示してみる。すなわち、ドラマの主人公達のようにとてつもなく魅力的な二人が恋に落ちた場合である。一般人とは違う二人が恋に落ちたら、果たしてどのような行動を示すのであろうか?この場合のパラメータは以下に示す、
- 「男」位置=5, 速度=0,魅力=1000,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=1000,優柔不断度=10
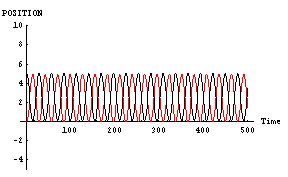 |
「魅力ある二人が恋に落ちた場合には、あまり近づかない方が良い」という教訓をここから得ることができる。
最後に、「男」と「女」の二人ともにあまり魅力がない場合である。パラメータとしては、
- 「男」位置=5, 速度=0,魅力=2,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=2,優柔不断度=10
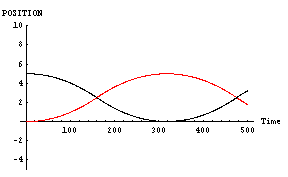 |
これなど「恋」と言えるのかどうかもわからない位である。ほとんど、「ただすれ違っただけの相手」である。これがさらに進むと、魅力がお互いに0同士のパターン、
- 「男」位置=5, 速度=0,魅力=0,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=0,優柔不断度=10
 |
これっぽっちも「男」と「女」は「恋」に落ちていないのである。これではカップルの「男」と「女」ではなく、単なる他人である。
さて、今回は行わなかったが、カップルに「恋のエネルギー損失」を導入することにより、「恋の無限摂動」を減衰させることができる。それにより、現実のカップルの行動にさらに近づくことができるのではないかと、私は考える。何らかの抵抗が生じることにより、「恋の無限摂動」が減衰するのだ。そして、二人は接近した状態で停止するわけだ。
さて、今回の登場人物は「男」と「女」だけであった。しかし、現実でも、ドラマの中でも、通常は多くの登場人物が登場する。登場人物が「男」と「女」だけというような理想的な条件のみではない。
人の恋路を邪魔する(主人公からすれば)ヤツも必ず登場する。また、特定の登場人物の間では斥力が働くだろう。そのような場合、一体どのような現象が生じるのだろうか。
そもそも、今回の恋する二人の行動パターンは予測可能であったが、現実そのようなことがあるだろうか?果たして、未来の行動パターンは予測可能なのだろうか?色々な登場人物が現れる場合にも、今回の結論は成立するのだろうか?
それらは次回の課題にしておく。題して、「恋の力学 三角関係編- 恋の三体問題- (仮称)」である。「恋の力」を一般化し、多体問題として解いてみたいのである。恋する人達とその周りの人達がどのような行動をするか、恋の三角関係においてどのような力が働いているのか、について解析を行ってみたい。今回は、そのための前準備というわけである。
1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
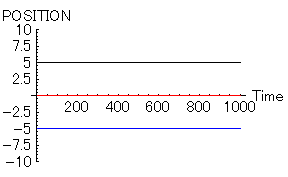 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
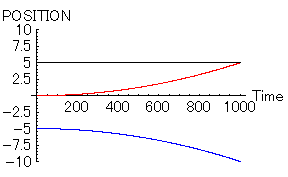 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
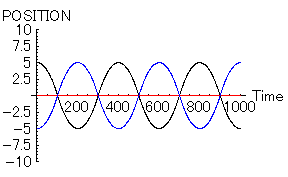 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
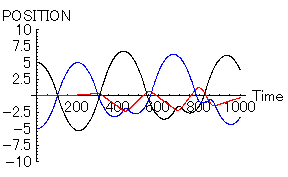 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)
2000-07-02[n年前へ]
■続 オッパイ星人の力学 
揺れる胸の動き編
前回、「オッパイに関する力学的なつり合い」を考えてみた。そして、
- 「バストに関するフックの法則」
- 「バストに関するヤング率」
さて、前回登場した私の友人のオッパイ星人ではないが、「通り過ぎる女性の胸をに目を奪われる人々」は多い。街中を歩いているオッパイ星人達を見分けるのは簡単である。視線が妙に上下・左右に揺れ動くヤツを見つければ良いのである。しかも、何人ものオッパイ星人達がそろいも揃って全く同じ目の動きをしているから、すぐ判るのである。もし、オッパイ星人達が地球征服を企みはじめた場合には、オッパイ星人達の目の動きにより地球人と区別する方法を私は提案してみたい。
しかし、「視線が妙に上下・左右に揺れ動くヤツ」といっても、それがどのような動きなのか知らないことには困ってしまう。もしかしたら、単に落ち着きのない一般人かもしれない。無実の人間にオッパイ星人疑惑をかけるわけにはいかない。オッパイ星人達の目がロックインしているバストの動きを知らないことには、オッパイ星人達の企む地球征服を阻止することはできない。
そこで、「私は正義、そして地球防衛のために」、歩いている最中の「バストに関する動力学」を考えてみることにした。歩いている最中の「バストの動き」を研究することにより、オッパイ星人の識別、ひいてはこの地球を守りたいと切に願う次第である。この私の目的をくれぐれも忘れないで頂きたい。
まず最初に、歩いている時の人の胸板の動きを考えてみることにしよう。一秒間の間に、
- 左足で一歩 -> 右足で一歩
 |
当然、この動きを見て違和感を感じる人がいるだろう。人は歩くときに、足先を円の中心にして進んでいくのだから、次の図のようにSin関数の絶対値をとったような形状になるのではないか、という考え方である。
 |
しかし、私は二つの理由により、この一見自然らしく思える「人の胸板の上下の動き」を採用しないことにした。
まず第一に、人間の足、胴体にはクッションのような働きがあり、この形状のように鋭い変化はしない、としたいのである。実際、街中を歩く人々を観察した結果でも先に示したような「人の胸板の上下の動き」であった。
第二に、この一見自然らしく思える「人の胸板の上下の動き」だと計算が面倒なのである。これでは私が困ってしまう。
というわけで、二つも問題がある考え方を採用するわけにはいかず先に示した人の胸板の上下の動きを用いることにした。
そして、その時の「人の胸板の左右の動き」を示すと次のようになる。
 |
さらに、この胸板の軌跡を女性の前方から眺めると次のようになる。想像力が豊かなオッパイ星人であれば、もうこの図に視線が釘付けのハズである。これが、上下左右に動くバストの土台としての胸板である。
 |
これはまるで指揮者が振るタクト、指揮棒のようである。この胸の土台が振るタクトに合わせて、我らがバストは揺れ動くわけだ。それでは、このように「胸板」が動くとした時に、
- 「バストに関するフックの法則」
- 「バストに関するヤング率」
 |
これが揺れるバストの動きのプロットである。ということは、これがオッパイ星人が揺れるバストに視線をロックインしているときの視線の動きでもある。そう、忘れているかもしれないが、「私は正義、そして地球防衛のために」、「オッパイ星人」を見分けるためにこの研究をしているのである。
そして、これが走っている状態ともなれば、こんな感じだ。これは1秒で6歩であるから、かなり速く走っている状態に揺れ動くバストの軌跡である。そう、あなたもよく街中で見かけたことがあるはずのあのバストである。この小気味良いリズムはどうだろうか。
 |
このグラフを見ても、なんてつまらないグラフだと思う人もいるかもしれない。そういうアナタは安心して大丈夫である。確かにあなたは普通の人間である。しかし、「この小刻みに揺れる動き」に美を感じる人がいたならば、あなたは少しヤバイ状態である。そうオッパイ星人の可能性がある。
そして、もしあなたが街中で視線をこんな感じで小刻みに揺らすヤツを見かけたら、そやつは人間ではない。オッパイ星人のはずである。要注意だ。私と一緒に正義・地球防衛のために戦って欲しい。
ただひとつ心配事があるとしたら、この研究をしているうちに「正義の味方であるこの私」の感受性が豊かになってしまったことである。妙にこのグラフに美を感じ始めているのである。そして、妙に文章に気持ちがこもっているような気がしてきたのである。いや、まさかとは思うが...
ところで、今回の計算はバストの動きが「バストに関するフックの法則」で決まるものとしている。つまり、バストを胸板に拘束する力がバストの弾性だけという状態である。簡単に言えば、全てノーブラ状態で計算を行っている。パラダイスである。いや、むろん私にとってではなくて、オッパイ星人にとってである。
オッパイ星人の力学はまだ始まったばかりだ。正義・地球防衛のために、私は研究を続けるのである。
2000-08-16[n年前へ]
■エアコンの風は心地よく吹くか? 
真夏の夜の夢 流体力学入門編
私は長野県の野辺山という高原で幼い時期を過ごしたせいか、暑さにとても弱い体である。なので、真夏の夜はエアコンが欠かせない体と根性になってしまった。エアコン無しではろくな夢が見られ無いどころか、眠れなかったりするのである。気持ちの良い「真夏の夜の夢」を見るためには、エアコンがとっても重要なのである。
つい先日、そんなエアコンの話題が「今日の必ずトクする一言」に載っていた。それが、
- エアコン用流体素子(PATPEND.)のナゾ
- ( http://www.bekkoame.ne.jp/~jh6bha/higawari.html#000819 )
- 復活する冷蔵庫脱臭剤のナゾ(1/f揺らぎと活性炭編)
- ( http://www.bekkoame.ne.jp/~jh6bha/higawari.html#000901)
(おそらくhiraxさんあたりがやってくれるのではなかろうか)と話題のパスまでされている。いきなり、ボーとしているところを授業で当てられた気分である。
とはいえ、「エアコンの流体力学」というのもちょっと興味のある話題でもあるし、パスされたからにはやってみなければなるまい。そういうわけで、真夏の眠れない夜のパズル代わりに挑戦してみることにした。
さて、部屋の中の「エアコンから送られる風の様子」を計算するということは、流体力学の計算をするということになる。流体力学の運動方程式(ナビエ・ストークス式)に代表されるような方程式群を解かなければならないのである。そこで、以前
の時にいじりかけたMichael Griebel氏らによる非圧縮性流体のNast2Dのコードをもう一度引っ張り出して使ってみることにした。このNast2Dは非圧縮性二次元流れを計算する教育用のソースコードである。詳しくは- TUM INFO V- Homepage - ( http://www5.informatik.tu-muenchen.de/home_us.html )
- Numerical Simulation in Fluid Dynamics A Practical IntroductionISBN 0-89871-398-6
計算するモデルは次の図に示すような部屋である。四畳半一間であるかもしれないし、100畳以上の大きな広間かもしれないが、とにかく正方形の部屋だ。向かって左の青い丸部分にはエアコンがあり、そこから冷たい空気が送られてくるのである。そして、この部屋には何故かタンスがおいてある。「やっぱり、この部屋は四畳半一間じゃないの」というツッコミは言ってはいけない約束である。とりあえず、このタンスが向かって下側にある紫の部分である。このタンスが、エアコンから送られてくる冷た〜い空気流の障害物となるのである。
 |
暑い真夏の夜に、こんな部屋をエアコンで涼しくする時のことを考えてみよう。気持ちよく眠るために、何はともあれエアコンのスイッチを入れるわけだ。そうしないと、暑くて眠れないから当然である。
そして、そのエアコンには送風モードが何故か三つあるのだ。次のような三種類の送風、
- 真っ直ぐ送風するモード
- 単純な首振り送風をするモード
- 山本式エアコン用流体素子を用いた送風をするモード
空気流の速度分布の計算結果を次に示してみよう。
|
| を用いた送風の場合  |
また、これらの場合の計算結果を動画で示したものをMPEG4形式のAVIファイルとReal形式のファイルにしたものを以下に置いておく。エアコンから空気が送られる様子を知るには、何はともあれこの動画を見て頂きたい。なお、手元のRealProducerの制限のために、このReal形式のファイルは古いバージョンのRealPlayerだとアップデートが必要になってしまった。また、MPEG4のCodecが導入されていない場合には、DivXなどをインストールする必要がある。
とりあえず
- 真っ直ぐ送風している場合 MPEG4 AVI ( 289KB ) Real形式( 73KB )
- 単純な首振り送風の場合 MPEG4 AVI ( 577KB ) Real形式( 89KB )
- 山本式エアコン用流体素子を用いた送風の場合 MPEG4 AVI( 693KB ) Real形式 ( 92KB )
また、それぞれのMPEG4形式の動画のファイルサイズを見れば、それぞれの場合の送風による空気流の速度分布の複雑さは一目瞭然である、と思う。真っ直ぐ送風している場合はとにかく単純な速度分布であって動画ファイルサイズも結果的に小さくなっているのに対して、山本式エアコン用流体素子を用いた送風の場合はかなり複雑な速度分布になっていて動画ファイルも結果的に大きくなっているのである。
動画を見ることができない人のために、それぞれの場合の連続した3つの瞬間における部屋内の空気流の速度分布の静止画も示しておく。
1 | 1 | を用いた送風の場合 1  |
 |  |  |
 |  |  |
これを見ると、「真っ直ぐ送風している場合」にはエアコンの正面は強烈に風が当たっている(つまり冷えまくっている)ことがわかるが、タンスの陰になっている部屋の隅などはほとんど空気が動いていないことがわかる。また、「単純な首振り送風の場合」は送風方向を動かしているとはいえ、その送風方向の変化はかなりゆっくりであって部屋の中の空気流の速度分布はそれほど急激には変化していないことも判ると思う(そういう風に計算しただけではあるが...)。いずれにせよ、もしもこの部屋の中にあなたがいたとしたら、体の決まった部分にのみ冷た〜い風があたることになるわけだ。それは体にはちょっとよろしくなさそうである。
一方、「山本式エアコン用流体素子を用いた送風の場合」は時々刻々と送風方向が変化しており、まるで部屋を舐め回すかのように、冷た〜い空気が送られていることがわかると思う。この部屋の中にもしあなたがいたとしても、体のごく一部分だけに冷たい風が当たるようなことはなく、それほど体に悪くないことが予想されるわけである。
さて、このページもかなり重いページになってきた。本来はこのタンスの裏側の空気が澱みやすい場所の「空気の入れ替わり」を、送風の具合を変えた上で調べてみたいわけであるが、それは次回のお楽しみ、ということにしておきたい。とりあえず、「真夏の夜の夢 流体力学入門編」はここら辺で終わりにしたい。
さて、夏休というわけでこんな景色のところで気持ちの良い風に吹かれてみたりするわけである。この写真の先の方の海の向こうに見えているのは左が伊豆半島で、右が三保の松原の辺である。

暑い夏の夜はエアコンが欠かせない体ではあるけれど、気持ちの上で言えばエアコンよりはおんぼろの扇風機の方が好きだし、扇風機よりも山の上の風の方がずっと好きだ。いつか、山の上を吹き抜ける風の音を録音して、その1/f揺らぎでも調べてみようかなと思うのである... それとも、そんなことをしてもツマラナイだけかな?
2001-01-27[n年前へ]
■オッパイ星人の力学 仏の手にも煩悩編 
時速60kmの風はおっぱいと同じ感触か?
本サイトhirax.netは「実験サイト」というジャンルに分類されることが多いようである。何が実験で、何が実験でないのかは私にはよくわからないのだが、とにかく「実験サイト」と呼ばれるサイトは数多くある。そして、その数ある実験サイトの中でも、人間そして愛について日夜取り組んでいるサイトの一つが「性と愛研究所」である。その「性と愛研究所」を読んでいると興味深いことが書いてあった。テレビ番組の「めちゃめちゃイケてる!」の中で何でも「時速60キロの風圧はおっぱいの感触である」と言っていたらしい。そしてまた、「性と愛研究所」では「おっぱいの感触と風圧に関する考察」の中で、「時速60kmでは全然おっぱいの感触ではなくて、ちょうど時速100kmを境に急におっぱいの感触を感じます。」というメールを紹介しながら、
「時速100kmの風では、本物は触れないけどお手軽に疑似体験、名付けて『プリンに醤油でウニ』ではなくなってしまう。それでは、まるで『キャビアにフォアグラでトリュフの味』だ。青少年のために疑似おっぱいを探してあげる必要があるな。」と結論づけている。
この「時速60kmの風」現象は「できるかな?」的にとても興味深いと思われるので、今回じっくりと考えてみることにしてみた。そして、この結論に何らかのプラスαをしてみたいと思う。
そう、前回「オッパイ星人の力学 第四回- バスト曲線方程式 編- (2001.01.13)」でオッパイの表面で働いている力について考えてみたのは、実は単に今回・そしてさらに次回の話のための準備だったのである。(さて、ちなみに今回は会話文体をメインに話が進む。「性と愛研究所」ではないが、この手の話は会話文体の方が書きやすいように思うし、私のバイブル「物理の散歩道」でも「困ったときの会話文体」と言われていたので挑戦してみた次第である。言うまでもないが、AもBも私が書いてはいるが、私自身ではない。)
A : 「東名高速で出勤途中に確認してみたんだが、やはり時速100kmあたりが妥当な感じだったな。」
B : 「何を根拠に妥当なのかがよくわからないが、確かに時速60kmでは手に何かが触っているという感触すらないな。それにしても、哀しい出勤の景色だぞ、それ。」A : 「ほっとけ!だけど、少し考えてみると、このおっぱい(ニセモノ)の感触問題は結構面白く、技術的にもなかなかに深い話だと思うんだよ。」
B : 「はぁそうですか…、としか言いようがないな。」A : 「まぁ、聞け。何しろこのおっぱい(ニセモノ)の感触問題には流体力学のエッセンスがぎっしりと詰まっているんだからな。」
B : 「そんな話は聞いたことはないが、とりあえず聞かせてもらおうか。」A : 「このおっぱい(ニセモノ)の感触問題を解くためには、とりあえず車の窓から手を出したときの指の周りの空気流を計算すれば良いわけだ。」
B : 「ちょっと待て。何で指の周りなんだ。手のひらじゃなくて?」A : 「簡単なことさ。試しにおっぱいを揉む仕草をしてみろよ。」
B : 「こ、こうか?あぁっ?手のひらじゃなくて指で揉んでるっ!」A : 「そうだろ。何故かわからないが、おっぱいを揉む仕草=Mr.マリックが超魔術をかける時のような指使いらしいんだよ。」
B : 「うむ、確かにそのようだな。」A : 「だから、時速60kmの風からおっぱいの感触を受けているのは指先だと考えるのが自然だろ。それなら、とりあえず下の図のような「指の間を抜けていく空気の流れ」を計算してみれば、おっぱい(ニセモノ)の感触問題が解けるわけだ。」
B : 「実写の手に二次元の計算結果を三次元的に合成するという凝った処理が、実にクダラナイことに使われている例だな…」
 | 高速で走る車の窓から手を出して、その手の指の間を抜けていく空気の流れを計算しよう。 鉛直方向の指の等方性を考えて、右の図に示すような指を輪切りにするような水平面のみを考える。 こんな写真を撮るときに、自己嫌悪に陥りがちなのは何故だか知りたい今日この頃。 |
A : 「こういう「空気の流れ」ような流体の力学は、ニュートンのプリンキピアに始まり、オイラーとベルヌーイにより非圧縮・非粘性の理想流体の運動方程式とエネルギー保存則が導かれた。それがオイラーの運動方程式とベルヌーイの式だ。オイラーの運動方程式はちなみにこんな感じだ。」
加速度 = 外力 + 圧力勾配力 v : 速度 |
A : 「基本的には「加速度 = 外力 + 圧力勾配力」という形だな。この非圧縮・非粘性の理想流体の場合はラプラシアンがゼロのポテンシャル流れと呼ばれる単純な流れになる。試しに、そんな場合をNast2Dを元にしたプログラムで計算してみた結果はこんな感じになる。ホントはこの計算自体は完全な理想流体ではないのだが、まぁ大体はこんな感じだ。」
B : 「おっ、あっという間に計算したな。」A : 「まぁ、ポテンシャル流れならエクセルでもちょちょいと計算できるくらいだからな。ちなみに、これは窓から手を出してしばらくしてからの空気の流れだ。」
 |
A : 「で、どうだ?」
B : 「いや、どうだ、と言われても困るが、なんかキレイだな。だけどちょっと小さくて見にくいなぁ。」A : 「そう言われれば確かにそうだ。じゃぁ拡大してみるか。」
 |
B : 「で、この結果から何がわかるんだ?」A : 「この図で空気は左から右へ流れているわけだが、左端の空気の速度と右端の空気の速度は、実は同じなんだ。」
B : 「そう言われても、よくわからないが?」A : 「指を通り過ぎてく空気は、指をとおる前後で運動量がそのまま変わってないってことさ。つまり、空気は指を通り過ぎる時になんら抵抗を受けてないってことだ。」
B : 「えっ?おかしいじゃないか、それなら逆に言えば指も空気から何の抵抗を受けないってことか?」A : 「そういうことだ。これがダランベールのパラドックスだ。」
B : 「じゃぁ、何か?この指先に感じるまぎれもないおっぱいの感触は幻だとでもいうのか!? そんなのオレは認めないぞ!」A : 「まぎれもない、っていうほどのものでもないし、ニセモノおっぱい自体は何か一種の幻のような気もするが、もちろん感触自体は幻であるハズはない。そもそも、空気をサラサラな理想流体として取り扱ったところが間違っているわけだ。そこで、登場するのがナヴィエとストークスだ。彼らはオイラーの運動方程式に粘性を導入した。全てはおっぱいの感触を説明するために、だ。」
B : 「それウソだろ。ナヴィエとストークスが聞いたら怒るぞ。」
加速度 = 外力 + 圧力勾配力 + 粘性力 v : 速度 |
A : 「見ればすぐわかるだろうが、この非圧縮流体に対するナヴィエ・ストークスの方程式は、最後に粘性項が入っている以外はオイラーの運動方程式と全く同じだ。」
B : 「なるほど。こうしてみると意外に簡単な式だな。」A : 「あぁ、オイラーの運動方程式に粘性項が入っただけだからな。そのせいで計算はちょっと複雑になるが、最近のパソコンならノープロブレムだ。というわけで、粘性を考慮して計算してみた結果が次の図だ。」
 |
B : 「おっ、ちょっと様子が違うな。何か、ジェットエンジンみたいに尾を引いてるぞ。」A : 「そうだろ。指の後ろのl様子がずいぶんと違うだろう。で、これを拡大してみたのが次の図だ。」
 |
B : 「左端の空気の速度はもちろんさっきと同じだが、指の後ろでは空気が渦巻いているし、右端の空気の速度は全然違うな。」A : 「もっとリアルに、窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみた計算結果のアニメーションが次の図だ。指の周りに空気が渦巻いていく様子がよくわかるハズだ。」
 | 窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみたもの。指の周りに空気が渦巻いていく様子がよくわかる。 メッシュを細かく切ったおかげで、計算結果は1GB弱。なんてこったい。 |
B : 「指が空気の中を走り抜いていく様子がよくわかるな。確かにこれなら、空気の抵抗を受けまくりだな。」A : 「そうだ。空気は指から力を受けるし、逆に、指は空気からしっかりと力を受けるわけだ。」
B : 「なるほど、この計算結果は指先に感じるまぎれもないおっぱいの感触を説明しているわけだな。いい感じじゃないか。流体力学そして粘性項さまさまじゃないか!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「おやっ?ちょっと待てよ!これでは、ただ現実を説明してみただけで、何の解決にもなってないぞ!時速60kmと時速100kmの風の感触の差を説明しているわけでもないし、青少年のためのもっと安全な擬似おっぱいを提供しているわけでもない!」A : 「いや、それがそういうわけでもない。実はこの先があるんだ。このナヴィエ・ストークスの方程式の解はレイノルズ数という無次元数によって決定されるんだ。今回の場合で言うと、レイノルズ数は「指の直径x 車の速度 / 流体の運動粘性率」という形になる。そして、このレイノルズ数が大きくなるほど渦が延びていくんだ。」
B : 「なるほど、わかってきたぞ。つまりあれだな。時速60kmから時速100kmに速度を上げれば、それに応じてレイノルズ数が大きくなって、空気の渦もおおきくなるし、おっぱいの感触も確実なものになるわけだな。勉強になるな。」A : 「う〜ん、実際には密度の違いの方が大きいんだが、ナヴィエ・ストークスの方程式の理解としてはそれでいいかもな。あと、単にレイノルズ数を大きくしたかったら指を太くする、っていうのでもいいわけだ。」
B : 「そう言われても指の太さはなかなか変えられないしなぁ。」A : 「指サックとか色々手はあると思うが、もっといい方法がある。さっきの式を眺めてみれば流体の運動粘性率が小さくなれば、レイノルズ数は大きくなる。例えば、水の運動粘性率は空気のそれの十五分の一だ。」
B : 「ってことは、水の中だったら、レイノルズ数も大きいし、密度も大きいし、指先に抵抗を受けまくりってことだな。すると、水中で手を動かしてみれば、それは空気中の高速クルージングと同じってことになるな!」A : 「そうさ、風呂の中で手をひとかきすれば良いだけの話さ。何もわざわざ時速100kmの車の窓から手を出す必要はないんだ。実際、風呂の中で確かめてみたけど、なかなかイイ感じだ!」
B : 「時速100kmで走る車の窓から手を出すのに較べれば、風呂の中で手をひとかきすれば良いだけなんて、まさに青少年のためのもっと安全な擬似おっぱいだな!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「それはもういいっ言ってるだろ。」A : 「ところで、ふと考えてみたことがあるんだ。さっき、指を太くすれば遅い速度でもレイノルズ数が大きくなるって言っただろ。東大寺の大仏なんかかなり指が太いじゃないか。」
B : 「確かに、そうだな。」
A : 「今調べてみると、大仏の掌の長さは256cmだ。つまり普通の人間の10倍くらいある。だったら、指の太さも10倍はあるだろう。ってことは、ほんのそよ風が吹いただけでも、大仏の手にはしっかりとしたおっぱいの感触が感じられているんじゃないのかな?」
B : 「単に手が大きいから空気の抵抗も大きいだけどいう気がしないでもないが、指の長さもでかいしさぞかし超巨乳の感触かもしれんな!そう考えると、あの大仏の手も何か実にイヤラシイ手つきに見えてくるから不思議だな!」A : 「う〜ん、悟りを開いているから、指先のヘンな感触なんかには惑わされないんだとは思うけどな。しかし、案外と仏もそんな煩悩と日夜闘っていたりするのかもしれないなぁ。しかも、その煩悩がホントーにあるのかもよくわからない幻のような擬似おっぱいってところが面白くないか?大仏の指先は二十一世紀の煩悩そのものを暗示しているのかもしれん。仏の手にも煩悩ってところだな!」
B : 「言いたい放題だな、全く。」
さて、今回は「オッパイ星人の力学第四回 - バスト曲線方程式 編- (2001.01.13)」と繋がるところまで話が辿り着かなかった。おっぱいの表面張力、マボロシのような指先の流体力学、そして大仏の煩悩をめぐる大河ドラマは人生そのもののようにまだまだ続くのである。


