hirax.net::Keywords::「関数」のブログ

■続 オッパイ星人の力学　

揺れる胸の動き編

　前回、「オッパイに関する力学的なつり合い」を考えてみた。そして、

• 「バストに関するフックの法則」
• 「バストに関するヤング率」

　さて、前回登場した私の友人のオッパイ星人ではないが、「通り過ぎる女性の胸をに目を奪われる人々」は多い。街中を歩いているオッパイ星人達を見分けるのは簡単である。視線が妙に上下・左右に揺れ動くヤツを見つければ良いのである。しかも、何人ものオッパイ星人達がそろいも揃って全く同じ目の動きをしているから、すぐ判るのである。もし、オッパイ星人達が地球征服を企みはじめた場合には、オッパイ星人達の目の動きにより地球人と区別する方法を私は提案してみたい。

　しかし、「視線が妙に上下・左右に揺れ動くヤツ」といっても、それがどのような動きなのか知らないことには困ってしまう。もしかしたら、単に落ち着きのない一般人かもしれない。無実の人間にオッパイ星人疑惑をかけるわけにはいかない。オッパイ星人達の目がロックインしているバストの動きを知らないことには、オッパイ星人達の企む地球征服を阻止することはできない。

　そこで、「私は正義、そして地球防衛のために」、歩いている最中の「バストに関する動力学」を考えてみることにした。歩いている最中の「バストの動き」を研究することにより、オッパイ星人の識別、ひいてはこの地球を守りたいと切に願う次第である。この私の目的をくれぐれも忘れないで頂きたい。
 

　まず最初に、歩いている時の人の胸板の動きを考えてみることにしよう。一秒間の間に、

• 左足で一歩　->　右足で一歩

人の胸板の上下の動き
横軸 : 時間(秒)
縦軸 : 高さ(cm)

　当然、この動きを見て違和感を感じる人がいるだろう。人は歩くときに、足先を円の中心にして進んでいくのだから、次の図のようにSin関数の絶対値をとったような形状になるのではないか、という考え方である。
 

一見自然らしく思える「人の胸板の上下の動き」
横軸 : 時間(秒)
縦軸 : 高さ(cm)

　しかし、私は二つの理由により、この一見自然らしく思える「人の胸板の上下の動き」を採用しないことにした。
　まず第一に、人間の足、胴体にはクッションのような働きがあり、この形状のように鋭い変化はしない、としたいのである。実際、街中を歩く人々を観察した結果でも先に示したような「人の胸板の上下の動き」であった。
　第二に、この一見自然らしく思える「人の胸板の上下の動き」だと計算が面倒なのである。これでは私が困ってしまう。
　というわけで、二つも問題がある考え方を採用するわけにはいかず先に示した人の胸板の上下の動きを用いることにした。

　そして、その時の「人の胸板の左右の動き」を示すと次のようになる。
 

人の胸板の左右の動き
横軸 :左右ｓ(cm) 
縦軸 : 時間(秒)

　さらに、この胸板の軌跡を女性の前方から眺めると次のようになる。想像力が豊かなオッパイ星人であれば、もうこの図に視線が釘付けのハズである。これが、上下左右に動くバストの土台としての胸板である。
 

人の胸板の軌跡
横軸 : 左右(cm)
縦軸 : 高さ(cm)

　これはまるで指揮者が振るタクト、指揮棒のようである。この胸の土台が振るタクトに合わせて、我らがバストは揺れ動くわけだ。それでは、このように「胸板」が動くとした時に、

• 「バストに関するフックの法則」
• 「バストに関するヤング率」

Gカップバストの軌跡 (1秒で2歩の場合)
横軸 : 左右(cm)
縦軸 : 高さ(cm)

　これが揺れるバストの動きのプロットである。ということは、これがオッパイ星人が揺れるバストに視線をロックインしているときの視線の動きでもある。そう、忘れているかもしれないが、「私は正義、そして地球防衛のために」、「オッパイ星人」を見分けるためにこの研究をしているのである。

　そして、これが走っている状態ともなれば、こんな感じだ。これは1秒で6歩であるから、かなり速く走っている状態に揺れ動くバストの軌跡である。そう、あなたもよく街中で見かけたことがあるはずのあのバストである。この小気味良いリズムはどうだろうか。
 

Gカップバストの軌跡 (1秒で6歩の場合)
横軸 : 左右(cm)
縦軸 : 高さ(cm)

　このグラフを見ても、なんてつまらないグラフだと思う人もいるかもしれない。そういうアナタは安心して大丈夫である。確かにあなたは普通の人間である。しかし、「この小刻みに揺れる動き」に美を感じる人がいたならば、あなたは少しヤバイ状態である。そうオッパイ星人の可能性がある。

　そして、もしあなたが街中で視線をこんな感じで小刻みに揺らすヤツを見かけたら、そやつは人間ではない。オッパイ星人のはずである。要注意だ。私と一緒に正義・地球防衛のために戦って欲しい。

　ただひとつ心配事があるとしたら、この研究をしているうちに「正義の味方であるこの私」の感受性が豊かになってしまったことである。妙にこのグラフに美を感じ始めているのである。そして、妙に文章に気持ちがこもっているような気がしてきたのである。いや、まさかとは思うが...

　ところで、今回の計算はバストの動きが「バストに関するフックの法則」で決まるものとしている。つまり、バストを胸板に拘束する力がバストの弾性だけという状態である。簡単に言えば、全てノーブラ状態で計算を行っている。パラダイスである。いや、むろん私にとってではなくて、オッパイ星人にとってである。

　オッパイ星人の力学はまだ始まったばかりだ。正義・地球防衛のために、私は研究を続けるのである。
  

■ブランコの中の∞(無限大)　

なんで一体漕げるのだろう？

　もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。

　やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう？口で上手く説明できる人がいるだろうか？

　それに、そもそも私たちはブランコを何故漕ぐことができているのだろう？

　いったい、いつから疑問に思うことをやめてしまったのでしょうか?　いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?
　いつだって、どこでだって、謎はすぐ近くにあったのです。
　何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。

　もちろん、「何でブランコの漕ぎ方が不思議なのさ？」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。

　次の図は「ブランコを漕いでる子供」である。
 

ブランコを漕いでる子供

　この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか？それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。

　だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか？

　次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、

1. ブランコの動きの中心を向いている軸A
2. 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B

ブランコに乗ってる子供を中心にとった座標軸

　ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。

　それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。

　というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。

　ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか？　この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
 

　まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか？
 

ブランコに乗ってる子供が立ち上がったりすると、何が起きる？

　「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。

　もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ！)上がれば、ブランコの速度はもとの速度の倍になるのである！

　ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。

　もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。

　もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ！
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。

　このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
 

　そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、

1. 初期のブランコの速度 = 10
2. 重心位置を高くして 10 X 2 = 20　(やったぁ、速度が二倍だぁ！)
3. 重心位置を低くして 10 Ｘ 1/2 = 10　(何てこったい、速度が半分になっちまったか！)

1. 初期のブランコの速度 = 10
2. 重心位置を高くして 0 X 2 = 20　(やったぁ、速度が二倍だぁ！)
3. そのあとブランコの速度 = 0
4. 重心位置を低くして 0 Ｘ 1/2 = 0　(0が0になっても全然変わってないもんね！ヘヘン！)

　人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
 

　なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。

　まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。１万円×２=二万円では１万円しかもうからないが、一千万円×２=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。

　もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。

　そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね！となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。

　というわけで、

• ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
• ブランコが上に行ったときにその姿勢を元に戻す

　それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。

　というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ

1. 何もしない場合
2. ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
3. ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合

ブランコの動きのシミュレーション結果

1. 何もしない場合 →　ブランコの動きはず〜と変わらない

2. ブランコが下にきたあたりで立ち上がり、 ブランコが上にきたあたりで座り込んだ場合 →　ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」

3. ブランコが下にきたあたりで座り込み、 ブランコが上にきたあたりで立ち上がった場合 →　ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」

　この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。

　ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
 

　さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか？　それとも、ちょっと考え過ぎかな。
 

■遠い空のはて？　

地平線の向こうに手を伸ばせ

　先日、富士山の五合目へ行った。と一言で言っても、富士山の五合目にも色々ある。何しろ上り口が、第一人気の「吉田口・河口湖口」、下りの「砂走り」で有名な「御殿場口」「須走口」、そして測候所の白ドームを目指し最短距離一直線の「富士宮口」と四種類もあるのだ。その色々ある五合目の中で、先日私が行ったのは富士宮口の五合目というところだ。富士山の太平洋側から富士山頂に向かう登山口の標高2400m地点ということになる。もしかしたら、表富士五合目と言う言い方のほうが有名なのかもしれない。

　その表富士五合目から下を眺めると、ずいぶんと遠くまで見えることに本当に心からビックリした。雲が下のほうに広がっていて、そしてその向こうに海や山や地平線が見える。そして、気のせいか地平線がとても丸いような気がする。その五合目までは車で簡単に来ることができたのだけれど、さすが標高2400mは伊達ではなかった…。やっぱり富士山は日本一の山かもしれない…。そして、そんな景色を眺めているうちに、私は色々考えてしまった。
 

　あぁ、下を眺めると遠くまで景色が本当にきれいだ。そういえば、眺めると言えば…

　これまで、私は急な階段の下から上を眺めたらスカートの内側の下着なんかを覗けるかどうかをジックリ考えてみたりしてきたなぁ。それに、SONYの誇る可愛いらしいAIBOの気持ちになって、やっぱり同じく低いAIBOの視点から上を見上げたらやっぱりスカートの内側が覗けるかどうかを考えてみたりしたなぁ。見上げてばっかりだなぁ、しかも、どれもスカートの内側かぁ…。
　そういえば、透け透け水着もマズかったなぁ…。あれ、本当に仕事の話から始まったんだけどなぁ…。誰も信じてくれないし…。

　あぁ、だけど、やはりそんなことを考えていてはいけなかったんだ…。そんなことをしてたから、画像処理追求サイトを目指したハズだったのに、何時の間にか有害サイト認定されてしまったりしたに違いないんだ…。ついには、「こどもに見せられないページ」保証までされたりするしなぁ…

　私は一体何処で間違えてしまったのだろう…？　あぁ、それにしても地平線がきれいだ…。地平線が丸い…。　あぁ、地球はやっぱり丸いんだなぁ…。

　と、まるで「生きる」で「ブランコに乗りながら人生を振り返る」志村喬のように、我が身を振り返っている内に、ふと「そういえば、地平線って一体どのくらい向こうにあるんだっけ？」と考えはじめてしまった。そもそも、地球が丸いからどうしてもある距離以上は見通すことができなくて、それが地平線なわけだけど、それは一体どのくらい先なのだったのだろうか？

　おぼろげな記憶を辿ると、意外に地平線は自分の近くにあって、確かほんの数km先程度だった気がするのだけれど…。さて？あれ？ はて… 果て…？

　というわけで、地平線までの距離を計算してみた。まずは、そのために下図のように視点の高さYと地球の半径Rをとってやる。
 

地平線までの距離を計算するために…

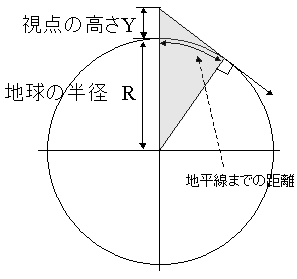　「視点位置」と「地球中心」と「地平線」を結んだ三角形（グレーで塗りつぶした部分）がもう簡単なくらいに直角三角形なことに注目して解いてみると、「地平線までの距離」は「視点の高さY」の関数として

というような形になる（計算が合ってれば…）。これに、地球の半径R = 6400kmを代入してやれば、視点の高さYに応じた地平線までの距離が求められるわけだ。

　そこで、まずは視点の高さが0〜3m位までの場合をグラフにしてみたのが次の図である。歩き始めて広い世界で暴れだすだろう頃の一才児の身長を緑○、そして、かつてはデカイの代名詞といえばコイツという存在だったアンドレ・ザ・ジャイアントの身長223cmを青○で記入してみた。
 

視点の高さが0〜3m位までの場合の地平線までの距離( km )

みどり：歩き始める位の一才児の身長 = 70cm 青：アンドレ・ザ・ジャイアントの身長 = 223cm

　このグラフを見ると、一才児の地平線はおよそ3km先にあって、アンドレ・ザ・ジャイアントの地平線は5〜6km先にあることがわかる。もちろん、その間の身長の人達の地平線はその中間、そう4km先くらいにあるわけだ。私たちの地平線はほんの4km先、なんと走ればほんの20分位のところ、歩いても一時間かからない程度の近くに地平線はあるのだった。地平線なんていうと、遥か遠くにあるように思えるけれど、手の届くほんのすぐ先にいるのである。

　そして、歩き始めた子供の地平線と巨人アンドレ・ザ・ジャイアントの地平線がたいして変わらない、というところも面白いものだ。あれだけ背が高ければ、さぞかし広い世界を眺めているのだろう、と思ったりするがそういうわけでもないのである。

　じゃあ、もう少し高い場所に行くとどうか、ということで1000mまで視点の高さを上げてみたのが次のグラフである。東京タワーの特別展望台の250mを緑○で、あくまで計画中の秋葉原タワーの特別展望台の500mを青○で示してある。　ここまで上がると、250m地点で地平線は60km先になり、500m地点では80km程度先まで見通せることになる。東京駅の位置からの距離で言うと、60kmでは箱根くらい、80kmで三島くらいだろう。
 

視点の高さが0〜1000m位までの場合の地平線までの距離( km )

みどり：東京タワーの特別展望台 青：計画中の秋葉原タワーの特別展望台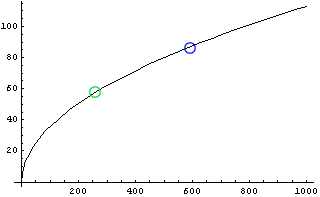

　調子に乗って、さらに視点を高くしてみよう。先の表富士の五合目2400m地点では200km近く見渡せ、東京駅からの距離で言うと地平線は遠く浜名湖辺りまで離れていく。そして、さらにさらに視点を上昇させ、ジャンボジェット機の巡航高度地上10kmからであれば、なんと350kmほども見渡せるのである。350kmだと東京駅から京都くらいだろうか。東京-京都と言えば、そうちょうど東海道五十三次だ。江戸時代の人達が一月近くもかけて歩いたくらいの彼方まで地平線は後ろへ下がっていくわけだ。地平線は時が流れるにしたがって、遠くに広がっていくのだ。
 

視点の高さが0〜10km位までの場合の地平線までの距離( km )

みどり：表富士の五合目 青：ジャンボジェット機の巡航高度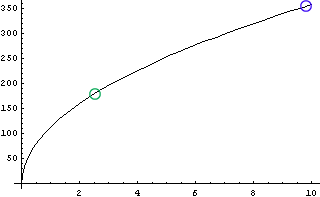

　そのジャンボジェット機から見える地平線は、かつては一月近くもかけて歩いたくらいの遠く、400kmも遠くなのだから、そこまで行くと地平線が「遥か遠く」に思える。一瞬そう思える、のだけれど実はそんなことはない。ジャンボジェット機の速度からすれば、そんな遥か彼方の地平線だって、やっぱり30分ちょい位のすぐ近くだ。私たちが普通に立っているときの地平線が4〜5kmくらいのすぐ近くにあって、歩いてみればやっぱり30分ちょいで行ける、というのとほとんど同じなのだ。
 

　五歳くらいの子供の地平線と、空を飛び回るジャンボジェット機の地平線を時間を距離の単位として比較してみれば実はほとんど同じ遠さだ、というのは何だかとても面白い。大地の果てと天とが接っする地平線はとっても近くにあって、そこまで行くのにかかる時間は小さな子供でも巨大なジャンボジェット機でも同じなのである。

　「地平線」なんて言うと、まるで「手が届かないもの」の代名詞みたいに使われたり、あるいは「その先には何があるのかわからないもの」の代名詞に使われたりするけれど、ちょっと行こうとして見れば、片道30分ちょっとでその「地平線」まで辿りつくことができるわけだ。案外、遠くにあると思い込んでいるものも、手を伸ばしてみれば、もしかしたら手が届くものなのかもしれない。しかも、それは地平線まで辿り着く時間が小さな子供でも巨大なジャンボジェット機でも同じだったように、誰でもできたりするものなのかもしれない。

　もちろん、かつての「地平線」だった場所まで辿り着いたとしても、新しい「地平線」は視界の向こうに下がって行くわけなのだけれど、そこまでだってやっぱり歩けばほんの30分だ。遠い空の果て、地平線の向こうは、すぐそこだ。

■ASCII EXPORTフィルター解決編？　

　「関数呼び出し時のレジスタの保護」に関するCコンパイラの対応の差が犯人？ということにしました。とりあえず、VisualC++6.0でコンパイルすると98上ではクラッシュし、VisualC++5.0では問題なく動作することを確認。また、Photoshop4.0,6.0でも動作を確認。
　というわけで、Win9x,NT4(多分ね)用も作成しました。（リンク）　参考：下記リンク。（リンク）（リンク）

■「やおい」の評価演算子　

ベクトルの彼方で待ってて II

　東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか？

「福田Ｘ小泉っていうのは、結構上手くやっているのかな？」

「あれは、福田Ｘ小泉じゃなくて、絶対あれは小泉Ｘ福田なのー」

「福田Ｘ小泉と小泉Ｘ福田は全然意味が違うのー」

「そう。ただ、ちょっと政治の世界とは違う世界かも〜。政界じゃなくて、やおい界ではー。」

• やおい　→　一部の女性が好む「男性同士の恋愛もののストーリー」のこと
• Ｘ　→　やおいの世界で恋愛の関係を示す記号。例えば、AさんとBさんが恋に落ちるであれば、Aさん×Bさんと表す。で、ここで重要なのは先に位置する方が「攻め役」となって、後に位置する方が「受け役」となる…。つまり、例えばサド侯爵とレオパルド・マゾッホであれば攻め役がサド侯爵で、受け役がマゾッホなので、サド×マゾなのである。決して、マゾ×サドではない…

　で、日本酒を飲みながら、まだまだ続くその話に悪酔いしていると、「カップルの順序が重要なんだー」という言葉を聞いて、ふと中学の頃の数学の授業を思い出した。その頃、大学を出てまだ一年目の斉藤慶子似の数学の先生と話していたときに、「Hくん、あのね掛け合わせる順序が違うと結果も違っちゃう計算もあるのよ」と教わったことがあった。そんな言葉から私は未知の「数学の世界」をかいま見たりしたのである。　今考えてみれば、新任の斉藤慶子似の女性教師の個人授業なのだから、行列・ベクトルの掛け算の順序なんかじゃなくて、「もっと違う順序」を手取り足取り教えてくれても良かったんじゃないか、とか思ったりするし、そうすれば、私は未だ見ぬ「大人の世界」を覗き見ることができたのではないか、と思ったりもするのだけれど、そんなことは残念ながら無くて、私はただ「行列・ベクトルの世界」を覗いただけだったのである。

　で、そんな昔話を思い出したせいか、頭の中でこんな風に思ったのである。そういえば、これまで「できるかな?」では数多く「恋の力学」でも遊んできた。ただ、そこでは「惹かれ合う恋心の大きさ」だけに注目して、そのカップルの中での役割などは考えたことがなかった。そこで、今回は「やおい」のカップルの「役割・順序」に注目し、その「役割・順序」を評価する演算子を行列・ベクトルの掛け算になぞらえながら考えてみることで、これまでと同じく色々な「恋の形」を眺めてみたいと思う。
 

　まずは、色々な人物（実際の人物であったり、小説などの登場人物であったり）のタイプを二次元空間に配置しよう。「この人は結構攻め役が合いそう」とか「この人は絶対受け役が合うのだー」という適性を

1. 攻めベクトル
2. 受けベクトル

SM平面上のサドくんとMくん

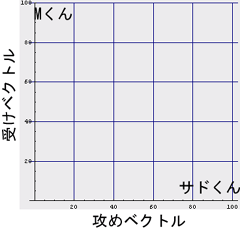　そして、カップリング適性では「A×B、B×Aが全然違う」ということから、外積(ベクトル積)をそのまま流用して、適当な評価関数を作ってみるのが自然だろう。まず、

カップリング適性ベクトル = （攻め度(s)、受け度(m)）

A×Bのカップリング適性 = ( As * Bm - Am * Bs )
　　　　　　　　　　　　　　　 = Aさんの攻め度 * Bさんの受け度
　　　　　　　　　　　　　　　　　　- Aさんの受け度 * Bさんの攻め度

　とりあえず、今回はこの評価演算子を作成するところまでで終えたいと思うが、いずれこの「やおいの評価演算子」を武器にして、いつか（?）「やおいの世界= やおい界」に限らず、色んな数多くの恋の関係を目に見えるようにしてみたいと思う。そして、これまで数多く考えてきた「恋の〜シリーズ」を充実させていきたいと思うのである。

　ところで、今回のカップリング適性評価演算子は基本的に外積そのものである。つまり、この演算が返す値は「二人のベクトルでできる平行四辺形の面積」に等しい。つまりは、「二人のベクトルでどれだけ色んな違うことがきでるか」を示す尺度である。そして、その値は二人のベクトルが直交する時、すなわち二人のベクトルが重ならず独立である時に最大値となる。つまりは、「二人のベクトルが違えば違うほど大きく」なる。例えば、先の「サドくん×Mくん」であれば二人のS,M趣向が完全に正反対であったからとてもお似合いのカップルになったのである。

　これをいわゆる恋の話で考えてみると、とっても独立な二人、趣味が重ならない二人がお似合いだということになる。なるほど、そんなカップルも世の中にはたくさんいることだろう。そんな人達を「外積タイプのカップル」と呼ぶことができると思う。

　一方、趣味が重ならないカップルだけでなくて、世の中にはそれとは正反対の「趣味が重なる良いカップル」も数多くいる。それは「内積タイプのカップル」である。内積はA,Bベクトル間の正射影に比例する量であって、つまりは「二人の重なるベクトルの大きさ」である。それは例えば、相手の中に自分を重ね合わせるような「二人の重なる部分が二人を結びつけるようなカップル」なのである。

　「理系と文系」・「男と女」が対極的なものでも、相反するものでもないのと同じく、「外積カップルと内積カップル」も別に二つに分けられるようなものではないだろう。「外積タイプの恋」も「内積タイプの恋」が混じり合って、それぞれに良いところもあれば、危ういところもあって、などと想像してみるのも面白いに違いない。そして、さらにはもしかしたらベクトル空間で萌えることができるようになったりするかもしれない。
 

　そういえば、ふと考えてみると以前「恋の形を見た人は」で最後に引用した本橋馨子の「兼次おじ様シリーズ」は男性同士の恋の話だった。つまりは「やおい」の話だった。そこで、もう一度そのセリフを最後に飾って眺めてみようと思うのである。
 

「愛はどんな形をしているか知っているか？」

「見た事ないからわかりません。」

「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...
もし愛に優劣を決めるものがあればなんだろう？... 異性愛か、同性愛か、そんなものじゃない　　…たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」