1999-02-14[n年前へ]
■感温液晶でNotePCの発熱分布を可視化する 
熱いところで感じてみたい St.Valentine 記念
東急ハンズで実験材料をいくつか買った。その中から、感温液晶シートを使って計測を行ってみたい。
色が変わる材料というものは多い。温度により物質の色がかわる現象はサーモクロミズムと呼ばれる。光により色が変わるサングラスのような現象の場合はフォトクロミズム呼ばれる。けっこう、色々な応用を見かける。
通常の感温液晶はコレステリック(Cholesteric)効果により反射光のスペクトルが変わるため、色が変化する。
これが感温液晶シートである。よくで見かけると思う。
 |  |
さて、それでは感温液晶を使っていくつか測定を行ってみたい。まずは、NotePCの発熱分布を調べてみる。最近のNotePCはかなり熱くなるものが多い。暖かいというよりもアッチッチ状態になるものさえある。
それでは、
- Toshiba Libretto50
- Panasonic Let'sNote mini(AL-N4)
いずれも、感温液晶シートをNotePCの上に載せることにより、評価を行っている。今回は発熱分布を知ることが目的であるので定量的な評価は行っていない。もし、温度を定量的に行いたいのであれば、色と温度の対応曲線をあらかじめ測定する必要がある。
以下に結果を示す。
 |  |
 | 左上:上面 右上:上面の発熱分布 左下:下面の発熱分布 |
 |  |
 | 左上:上面 右上:上面の発熱分布 左下:下面の発熱分布 感温液晶シートのサイズがA4であるため、Let'sNote miniにちょうどフィットする。 |
Libretto50ではPCカードのNICを右に挿しているため、キーボードの右側部分の発熱が大きい。また、下面ではハードディスク部分の発熱がわかる。また、ク*ックア*プしているせいかかなりアッチッチである。
Libretto50,Let's Note miniいずれにおいても液晶のドライバーがある部分(液晶の左)は発熱が激しいのがわかる。
本来ならば、愛用しているTOSHIBA Portege320でも計測を行いたい所だが、ただいま長期入院中である。間もなく使用1年になるが、これまでに入院3回を経験し、入院期間は計2ヶ月にわたる。昔の小説家もビックリの病弱さである。他の使用者の話を聞いていても実に不安定な機種のようだ。一体、疲労骨折を経験していないPortege320というのは、はたして存在するのだろうか。あぁ...
今回は手元にあったNotePCでのみ測定を行ったが、近所の協力の下に色々なNotePCの発熱分布を調べる予定である。特にパームレスト周りの発熱分布などは割に軽んじられているだけに、興味がある。
今回は感温液晶を使った温度分布の簡単な可視化をしてみた。同じような測定は色々してみる予定である。
感温液晶と同じように、温度で変化する材料は多い。例えば、FAXでよく使用される感熱紙もそうである。
他にも、RICOHの熱可逆性情報表示フィルム
http://ext.ricoh.co.jp/saiyo/sin/prof/eyes/page4_2.html
などもそうである。
これなどはお店のポイントカードなどでよく見掛ける。私の財布から探してみると、オートバックスのポイントカードがこれと同じようなものである。70-130℃位の温度変化により透明度を変化させる材料である。これ位の温度であると、真夏の車中にカードを放置するとどうなるか心配なところである。
今回の情報に関連するWEB一覧
- 伊藤のホームページ(http://www.infonia.ne.jp/~itous/)
- 岡山県教育センター(http://www.pref.okayama.jp/kyoiku/sido/edu_cent/seminar/rika/rikasho/zikken.htm)
- お湯で変色するサーモクロミズム化合物をつくる(高橋 正)(http://www2b.biglobe.ne.jp/~murasho/news22.htm)
- 液晶について(http://www.osakac.ac.jp/labs/fujita/asai/ekisyo.html)
- 感温液晶を用いた非定常熱伝達の計測システムの基礎的研究(http://village.infoweb.ne.jp/~fwhz0564/kenkyu.htm)
- 感温液晶マイクロカプセルによる可視化(http://koneeko.linux.or.jp/AandO/gfd_exp/exp_j/tech/elc.htm)
1999-02-26[n年前へ]
■ヒトは電磁波の振動方向を見ることができるか? 
はい。ハイディンガーのブラシをご覧下さい
(1999.02.26)
リチャード・ファインマンの本の中で次のような問題があったように思う。
「偏光板がフィルターが一枚だけある。その偏光フィルターの偏光方向をどのようにして知れば良いか?」
その本の中での答えは、
「物体の反射光を偏光フィルターを通して見てみる。」
だった。ブルースター角で入射した光の反射光は、入射面に対して電場の振動方向が垂直になっている、ということを利用するわけである。
分かりやすいように、偏光フィルターを通してみたガラスの反射光をデジカメで撮影してみる。左が反射光を通すような角度に偏光フィルターを回したものであり、右が反射光をカットするような角度に偏光フィルターを回した場合である。この左の場合、すなわち、反射光が一番通過している角度から液晶の偏光面がわかるわけである。
 |  |
ところで、このようなファインマンが示したような方法を用いなくても、そもそもヒトは電磁波の振動方向を見ることができるのである。以前、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「鳥は太陽の位置、光の偏光パターンを位置のセンサーに使う」という話があった。ヒトも同じく光の偏光方向、すなわち、電磁波の振動方向を見ることができるのである。鳥はどう見えるかは私にはわからないが、ヒトならば自らが実験台になれるので、電磁波振動方向をどう見ることができるか調べてみたい。というわけで、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「近日中にある実験をする予定である」と書いたものが今回の確認実験である。なお、光の進行方向と磁界の振動方向を含む面を「偏光面」、電界の振動面を含む面を「振動面」と呼ぶ。
電磁波の振動方向をヒトが見ると「ハイディンガーのブラシ "Haidinger'sBrushes"」というものが見える。それを知ったのは、いつものごとく「物理の散歩道」からである。網膜に複屈折性があるために「ハイディンガーのブラシ」が見えるのだという。
私はこれまで、「ハイディンガーのブラシ "Haidinger's Brushes"」を見たことがない。いや、正確に言えば意識したことがない。そこで、判別しやすいように直線偏光を用意してやることにした。そこで、東急ハンズで偏光フィルターを買ってきた。
そして、空を見てみる。もちろん、偏光の偏りが強い、太陽を中心にして90度の角度をなす同心円方向である。詳しくは、
- 可視-赤外域での偏光観測による衛星観測手法の開発基礎研究(http://www.mri-jma.go.jp/Dep/sa/Lab1/labt01-s.html)
- エアロゾル観測(http://mars.im.kindai.ac.jp/KISYO/YPROJECT/kansoku.html)
さて、ヒトである私は、空を眺めて格闘すること5分程で、「ハイディンガーのブラシ"Haidinger's Brushes"」がわかるようになった。私が見たハイディンガーのブラシ"Haidinger's Brushes"を示す。
 |
この絵で太陽の方向は右上であり、偏光面は次の絵の青の矢印方向になる。
 |
というわけで、ヒト(少なくとも私は)電磁波の振動方向を見ることができるのである。慣れてしまうと、白い紙を見つめているときなども(条件によっては)見えるようになる。色を扱う人は意識すると面白いと思う。
ところで、偏光フィルターがどういうものか知らない人のために、NotePCの液晶に偏光フィルターを重ねた写真を示す。
 |  |
なぜ、こうなるかわからない方は、
などを参考にして欲しい。液晶ディスプレイの構造がわかると思う。そして、面白いことに気づいた。NotePCの液晶からの光は直線偏光である。ということは、NotePCの液晶にはハイディンガーのブラシが映っているのである。正確に言えば、NotePCの液晶を見ているあなたの視界の中央には、ハイディンガーのブラシが映っているのである。と、気づいてみると確かに見えている。
というわけで、液晶ディスプレイを使用している方はハイディンガーのブラシを見て頂きたい。以下のやり方がわかりやすいと思う。
1.このWindowを最大化する
2.下へスクロールして画面を真っ白にする。
3.液晶ディスプレイ(NotePC)を回転させる。
4.画面(視点)の中央に(視点に対して位置が)動かない黄色いもやが見えるはず。もちろん、回転はする。
液晶ディスプレイやヘッドマウントディスプレイ(HMD)を色々見てみたが、どれにもハイディンガーのブラシは存在していた。視界の中央に不思議な十字架のように現れているのである。現代の液晶技術が負う十字架である。
誰もが、目の前にあるのにそれに気づかないというのも、実に面白い。まるで、「青い鳥」のようである。そして、そういうことはとても多いのではないかと思う。それはそれで面白い話だ。
- それでは、ハイディンガーのブラシをご覧下さい -
2000-04-21[n年前へ]
■オレにはヤツらが見える 
スギの花粉は「見える?見えない?」
少し前まで、スギ花粉が飛びまくっていた。スギ花粉症の人にとっては、とても苦しい季節だろう。私の家族も結構スギ花粉症にかかっている。ということは、私もいつか苦しむことになるのだろう。いや、むしろブタ草を主因とする小児喘息で酸素吸入を繰り返した私であるから、まだかかっていないのが不思議なくらいである。
さて、私の勤務先でもスギ花粉で憂鬱になっている人は多い。ヒドイ(もちろん症状が)人などは、この季節になると、
「今日はスギ花粉がいっぱい飛んでいる。」と囁き始めるのである。毎日、である。そういう時に
「オレにはヤツらが見える。」
「ヤツらがオレに襲いかかってくるんだ。」
「誰かがオレの頭に電波を飛ばしてくる、という話に似ていますね。」などとチャチャを入れると大変である。
「スギ花粉症にかかっていないやつに何がわかる!」と言われてしまうのである。いや、確かに私には見えないのだ。ピンクの象が飛んでいるのが見えないように、スギの花粉も私には見えないのである。
「オマエら、スギ花粉症にかかっていないものに、所詮ヤツらは見えないんだ!」
「ほら、あそこにスギ花粉が見えるだろう」と指さす辺りを眺めても、私には何も見えない。ただ、ボンヤリした霞が見えるだけである。仕方がないので、そんな時には、なおさら
「普通の人には見えないところなんか、ホント電波と同じですね。」と言ってみたくなる。いや、私の性格からするともしかしたら言っているかもしれない。うん、言っているだろう。それどころか、
「その花粉を飛ばしてくるのは、宇宙人かナニかですか?」と、火に油を注ぐようなことを言っているに違いない。しかし、その性格は親譲りだ(坊ちゃんじゃないけれど)。
それはさておき、
「オマエら、スギ花粉症にかかっていないものに、所詮ヤツらは見えないんだ!」と言われているだけではくやしいので、私もスギ花粉を見てみたいと思う。当然である。あらゆるものを「目に見えるかたち」にするのが私の好みである。というわけで、可視化シリーズの始まりである。いや、可視化という言葉はどうも小難しく感じるので、名前を改めて「見える?見えない?」シリーズの続きである。これまで、漱石の小説、星の王子さまの内側、透け透け水着、ミニスカートの内側…などさまざまなものを「目に見えるかたち」にしてきたが、その続きというわけだ。
今回登場する、秘密道具はコイツである。
 |
この道具は、チンダル現象を利用して微粒子を可視化してくれるのだ。というと、小難しく聞こえるかもしれないが、とても簡単な原理である。光を微粒子に当ててその反射光を目で見るだけである。もちろん、微かな反射光を捉えるわけであるから、
- 微粒子からの反射光以外は目に見えないようにする
- ボケを小さくするために、絞りはできるかぎり小さくする
さて、それではコイツでスギ花粉(らしきもの)を見てみよう。暗闇に浮かぶ「スギ花粉(らしきもの)」が見えるのだ。
 |
こういった感じでスギ花粉(らしきもの)を可視化することができる。といっても、この微粒子がスギ花粉である保証は「全く」ないのであるが、あえて「スギ花粉(らしきもの)」としておくことにする。ちなみに、この画像もスギ花粉の最盛期に撮影したものである。とりあえず、こうすればスギ花粉症のあなたの敵、すなわちヤツらを目にすることができるのだ。敵であるターゲットの姿を知らずして戦うことはできないだろうから、スギ花粉症のあなたにはこの実験をすることを強く勧めたい。この画像はデジカメで撮影したのだが、実際に人間の目で見ると、ものすごい数の微粒子が飛び回っているのがわかる。今回見えた画像がスギ花粉かどうかはさておき、こういった微粒子は部屋の中ではほとんど見られない。しかし、戸外ではかなりの数の微粒子を目にすることができる。
もう一枚、参考までに示しておく。微粒子が動き回る様子が実感できるはずだ。こういう微粒子があなたの鼻や喉の粘膜に襲いかかってきているのだ。
 |
これらの飛び回る「スギ花粉(らしきもの)」を撮影したmpeg動画(115kB)をここにおいておく。スギ花粉症の人はぜひ敵であるヤツらを自分の目で確認して頂きたい。
さて、「可視化」シリーズ、改め、「見える?見えない?」シリーズはこれからも続く。ありとあらゆるものの「見える?見えない?」境界線を追求したい。どんなにクダラナイものであっても、あらゆるものを「目に見える」ようにしていきたいと思うのである。
2000-05-12[n年前へ]
■メガネの内側にある歪み 
隠れたストレスに光を当てろ
また、可視化の話である。いや、自分でも忘れていたが、「可視化」改め「見える?見えない?」シリーズである。今回はメガネの内側にある「歪み」、隠れたストレスに光を当ててみたい。そして、そこに何があるかを見てみたいのである。
私の眼はどうも明るさに弱い。やたら太陽の光が眩しく感じることが多い。といっても、単に私のガマンが足りないだけかもしれない。あるいは、睡眠不足のせいかもしれない。そして、私は同時に暗さにも弱いのだが、こちらは単にビタミン不足による鳥目だろう。
そういうわけで、明るいのに弱いので車を運転する時には大抵サングラスをかけている。サングラスは何本も持っているわけだが、最近のお気に入りはこれである。
 |
これは、偏光フィルター機能付のサングラスである。偏光というギミック付のところがお気に入りの理由である。以前、
で書いたように、偏光フィルターがあれば色々なものの反射光のみを遮ったりすることができる。例えば、下の右側の写真では左の写真に比べてガラス表面の反射光が減少していることがわかるだろう。これは偏光フィルターの作用のせいである。 |  |
これと同じように、偏光フィルター機能付のサングラスを使えば色々な反射光を防ぐことができる。例えば、通常は反射光などで車のフロントグラスの内側にいる人の姿はよく見ることができない。しかし、このメガネをかけていれば、反射光に邪魔されずフロントグラスの内側を見通すことができるのである。もう、対向車なんてまるでフロントグラスがないかのようである。
この偏光フィルター機能付のサングラスは、通常「釣り」などで用いられるものだ。水面の反射光を防ぐことにより、水中の魚の姿などを見やすくするためのものである。結構、海の近くに住んでいる私にはうれしい機能である。
このサングラスをかけている時に、ふとある実験を思いついた。普段は透明にしか見えない「普通のメガネ」の影に隠れたストレスを目に見える形にしてみようと思ったのである。よく、「メガネの奥にストレスが隠れている」というが、そのストレスを見て取れる形にしようと思うわけだ。
そこで、新婚ホヤホヤの「夜の帝王」I田氏(関係ないが、I田氏から「Hirabayashiさん、小杉のメーリングリストで-できるかな?-の話題が出てましたよ。」と言われた時はビックリした。とりあえず、どなたか知らないが、メーリングリストで紹介して頂いた武蔵小杉勤務の方には一言お礼を言っておきたい)にメガネを借りてみた。このメガネをじっくり眺めてみてもらいたい。
 |
この透明なメガネの奥に何か見えるだろうか?そこに「歪み」は見えないだろうか?「透明だから、何も見えないだろう。」という人もいるだろうが、あるグッズを使うと、もう明らかに見えてくるのである。それが、下の写真である。レンズを固定している辺りをよく見てもらいたい。不思議な
虹模様と十字の模様が見えるはずだ。
 |
プラスチック等は製造過程での不均一な応力や、外力により複屈折性を示す。光弾性と呼ばれる現象である。そのため、偏光面を直行させた偏光フィルターの間にそういうプラスチックなどを挟みこむと、その弾性体の内部に働いている応力分布の状態を調べることができる。それを応用したのが、偏光顕微鏡などである。
例えば、下の写真はカセットテープのケースの左側部分を、偏光面を直交させた二枚の偏光フィルターで挟んでみたものである。見事に弾性体の内部に働いている応力分布が可視化できているのがわかると思う。これを応用すれば、例えば熱変形をしているようなものであれば、透明体の熱分布も簡易的に見て取ることができる。
 |
そういうわけで、先の写真あるいはそれを拡大した次の写真のように普通では見えない透明なプラスチックレンズの中に隠れている「ストレス」を見て取ることができるわけだ。
 |  |
とりとめもないが、今回は透明なメガネの影に隠れたストレスに光を当ててみた。ちゃんと見ようと思いさえすれば、目に見えるものは数多くある。「見える?見えない?」の境界線はその人自身が決めるのである。「できるかな?」では、これからも色々な「見える?見えない?」を追求し、「見えるかな?」について考えていきたいと思う。
2003-06-17[n年前へ]
■アルキメデスのパンチラの式 
「スカート円錐」の明るさを探れ
「スカート円錐」の明るさを探れ
以前、「ミニスカートの幾何学」として、女子高生の間などで流行っていたミニスカートの丈の短さの限界について考えてみたことがある。階段を上ろうとしているミニスカートを履いた女性(別に男性でも構わないが…)の下着が見えてしまうかあるいは見えないのかを、女性達が履くミニスカートの丈の長さから考察をしてみたのであった。その「ミニスカートの幾何学」の考察をした結果、ミニスカートの丈がちょうど32cmの時に、ミニスカートで下着が隠されはじめる境界線がちょうど階段と平行になる、ということが判ったのである。そして「下着が隠されはじめる境界線がちょうど階段と平行になる」結果、ミニスカートの丈が32cmより短いと下着が階段下を上る人達から見えてしまうようになり、逆にミニスカートが32cm以上の丈であればスカートの中の下着はなんと幸か不幸か見えることはないのだ、ということが判ったのである。ミニスカートをはいた女子高生が急な駅の階段なんかを上るときでも、ミニスカートの丈が32cm以上であれば、パンチラの恐怖に怯える必要はないということが判ったのであった。
ところで、ミニスカートの中が見えてしまいそうになる場所というのは、必ずしも急な階段だけではないらしい。最近の東京の有名スポットなどでは、「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかがたくさんあったりするというのである。そして、そんな場所では、真上にいる「スカートを履いた女性」を急角度で仰ぎ見ることができて、スカートの中の下着がチラリと見えてしまうことがあるというのである。
しかし、である。角度的にスカートの中の下着が見えるからといって、果たして本当に下着が見えるものなのだろうか?角度的には見えるはずでも、実際には人間の目には見えないことだってあるのではないだろうか。なぜなら、スカートが「私たちの視線から下着が見えるのを遮っている」のと同じように、スカートは「照明の光が下着にあたるのをも遮っている」のである。スカートの中というのはスカートに光が遮られて(たぶん)かなり暗いハズなのである。いや、実際に覗いてみた経験があるわけでは決してないので自信を持って「ハズ」と断言することはできないのだけれど、スカートの中が明るいわけはないと思うのである。もし、スカートの中が明るくなければ、仮にその中身を覗くことはできても結局暗くて何も見えないわけで、「スカートの中が(見えるくらいに)十分に明るいかどうか」が肝心だと思うのである。そこで、今回は「下着が角度的に見通せる条件」ではなくて、「スカートの中の下着が十分明るく見える条件」を考えてみたい。
まずは、スカートをはいた女性を下の図のように簡単に示してみよう。スカートを下向きに開いた円錐として考えてみる。もちろん、スカートの中の下着はこの円錐の頂点に位置するわけだ。そして、スカートが広がる角度をΘとでもしてみることにしよう。その時、円錐の頂点にはどれだけの光が当たるものだろうか?
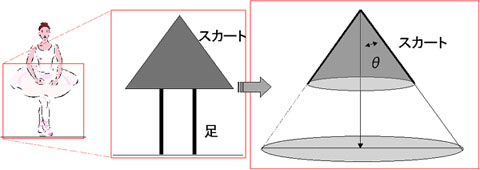 |
もちろん、円錐状のスカートが上からの光は遮っているわけだから、スカートの中の下着を照らす光というのは、下の床からの反射光だけである。つまりは、上の図で、「色を付けた部分の床」からの反射光のみが下着にまでたどり着き、それ以外の床からの反射光はスカートに遮られて、スカートの中を照らすことはない。ということは、「スカートの中はどれくらい明るいか?」という疑問を考えることは、それは「色を付けた部分の床からスカートの中の下着にまでたどり着く光がどれだけあるか?」ということを考えることと同じなのである。
そしてまた、床上での光の反射に方向性が無く、光が完全に等方的に周囲に拡散するとするならば、円錐の中心(つまりはスカートの中の下着部分だ)にあたる光の量は、下の左図の色を付けた部分球の面積に比例する。つまり、「スカートの中の明るさ」は「スカートの広がり角」で決められる「部分球」の面積に比例するのである。
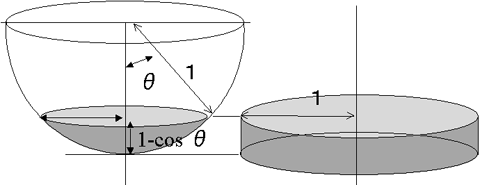 |
つまり、角度Θで広がるスカートの中が「どれくらい明るいか?」という疑問は、「下図で色を付けた部分球の面積はどのくらいか?」という問題に変わるわけである。「半球全体の面積に対して、スカートの広がりで決められる部分球の面積はどのくらいの割合か?」ということの答えが、それすなわち「スカートの中の明るさ」を決めているのである。
ところで、アルキメデスが発見したように、球(もしくはその一部)の面積はその球に外接する円筒の面積に等しい。つまり、上の図の左で色を付けた部分の面積というのは、右に示したような(色を付けた)円筒の面積に等しいわけだ。ということは、右の円筒部分の面積は
円筒の面積 = 2 π (1-cosΘ)であって、左の半球の面積が(直径=1とすると)2πだから、円錐状のスカートの中の明るさは、スカートの広がる角度をΘとするならば、「スカートの中の明るさ」は
という実に簡単な式で表されることになる。アルキメデスも、まさか自分の球と円筒の表面積に関する発見が「スカートの中の明るさを示す式(ここでは仮に『パンチラの式』とでも呼ぶことにする)」を導くために使われるとは想像だにしなかっただろうと思うが、とにかくアルキメデスのおかげで私たちはスカートの中の明るさを知ることができるのである。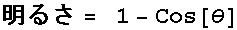
試しに、このくアルキメデスの『パンチラの式』を使って、スカートの広がり角度Θに対して、スカートの中の明るさがどのように変化するかを計算してみると、その結果は下のグラフのようになる。このグラフは、横軸が「スカートの広がる角度」で、縦軸が「スカートの中の明るさ」を示している。周囲の「照明に照らされている床」の明るさを1とした時の「スカートの中の明るさ」を示しているのである。
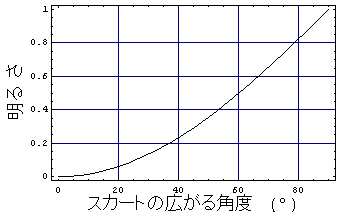 |
基本的にはスカートが広がるにつれて「スカートの中の明るさ」は明るくなるわけであるが、このグラフを眺めてみると、スカートの広がる角度が20°を超えるあたりから次第にスカートの中が明るくなることが判るだろう。例えば、スカートの広がる角度が30°の時には、スカートの中は「床の明るさの10%程度の明るさ」しかないが、スカートの広がる角度が60°にまで広がれば、スカートの中は「床の明るさの半分程度の明るさ」になる、ということが判るわけだ。
ところで、人間の目というものは「見るものの明るさ」に合わせて順応する。例えば、暗いものを見るときには目の感度は自動的に上がる。だから、スカートの中がほのかでも明るかったならば(例えば床の明るさの5%程度にでも明るければ)、自動的にその明るさに目が順応してスカートの中が見えてしまうかと思いきやそうはいかない(ハズだ)。なぜなら、人間の目は明るいものを見る時には、目の感度が逆に自動的に低下してしまうからである。スカートの中以外の明るい場所(例えば照明や、照明に照らされた明るい壁)だって、自動的に視界の中に入ってくるわけで、目の感度はそういう明るい部分に自動的に合ってしまうハズなのである。
例えば、下の画像は周りの明るさに対して、
- 5%の明るさ
- 10%の明るさ
- 20%の明るさ
| 5 % | 10 % | 20 % |
ということは、先のグラフで「スカートの中の明るさ」が10%を超えていないと、つまりは周囲にある明るい床(や照明や壁)などの明るさの10%を超えているくらいでないと、スカートの中が仮に幾何学配置的に見える条件であったとしても、実際には目の感度的にその中のようすを判別することができないに違いないのである。その場合、おそらく明るい床や壁の明るさに目の感度が合ってしまい、ほの暗いはずのスカートの中は真っ暗にしか見えず、幸か不幸かスカートの中身は識別することができないハズなのだ。
というわけで、先ほどのグラフに「識別できる明るさか否か」を書き入れてみると、次のグラフのようになる。
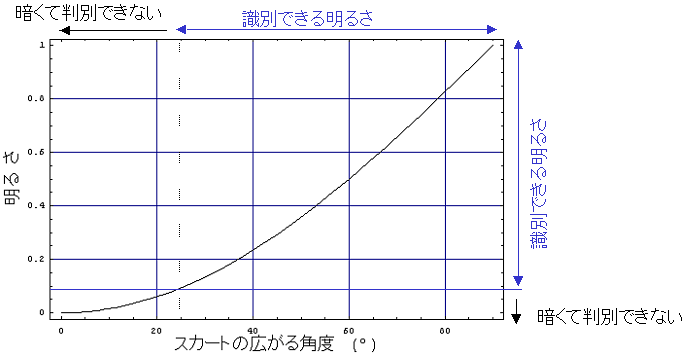 |
つまり、スカートの広がる角度が25-30°を超えていないと、スカートの中身は周囲の床や壁の明るさに比べて相対的に暗すぎて人間の目ではおそらく見ることができないのだ。
例えば、スカートの広がる角度が30°以下に制限されるようなタイトスカートを穿いて、明るい壁や照明などが視界にどうしても入ってしまうような場所にたたずんでいる限りは、もし仮にスカートの中を覗かれたとしてもスカートの中は(人間の目からすると)真っ暗で何も見えないわけで、スカートの中身を見られたりするような被害にあうことはまずないだろう、ということが先のアルキメデスの『パンチラの式』から判るわけなのである。「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかであったとしても、背後に明るく輝くものがある限りには、見る人の目を眩ませることができて、スカートの中身は安全なわけである。
ところが逆に、床が白かったりして明るいクセ(つまり下からの照明が強いクセ)に、周りに明るい壁や照明が何故かあまりないような場所がもしあったとして、もしそんな場所で(下から)スカートの中を覗かれたりしてしまうと、(下から覗く人の視界に入る)周囲の明るさに比べてスカートの中が十分明るく見えるせいで、しっかりとパンツの模様をチェックされてしまうということになるだろう、ということも予想することができてしまうのである。だから、そんな場所をもしも短いスカートをはいて歩かなければならないような場合には、例えば何かの「ピッカピッカ輝く光りモノ」でも身につけて、その光りモノの明るさを「スカートの中身をのぞこうとするスナイパー」の視界に入れて、彼らの目を眩ませてしまえば良いだろう、というアルキメデスの知恵さえ授けてくれるのだ。
ところで、今回は「スカートの中の明るさを示す=パンチラの式」を考えてみたわけであるが、この式は考えるまでもなく実にアブナイ式である。パンチラの被害防止に役に立ちそうな気もするし(全然役に立たないような気もするが)、逆に単なる「パンチラの科学」になってしまっているような気もしてしまう。「スカートの中身をのぞこうとするスナイパー」の魔の手から逃げるためのバイブルになるような気もするし、「スナイパー」のための手引き書になってしまいそうな気もする。ギリシャ神話で、あらゆる災厄が入っていたという箱がパンドラの箱だったけれど、このパンチラの式だって案外そんなパンドラの箱のような、色んな災厄の元になってしまうものかもしれないのである。しかも、パンドラの箱の場合には最後に箱の中に『希望』が残っていたわけでまだ良い(?)のである。しかし、アルキメデスの『パンチラの式』の場合には「スカートの中にだっては『希望』が入っているのだぁ」などと口に出したりしたら単に変態扱いされてしまうだけなわけで、そこはパンドラの箱よりもずっとたちが悪いのである。つまりは、科学もアルキメデスの『パンチラの式』も使う人次第なのである。