hirax.net::Keywords::「女子高生」のブログ

■めがねっこ大好き。　

めがねを外すと美人になるは本当か!?

理系＝めがねっこ大好き？

　「どんな時に自分を理系だと思う？」と文系人間に聞かれた。私は「うむむ…」と答えに詰まってしまった。そんな私に、その文系人間はまるで勝ち誇ったような表情で「じゃぁ、理系と文系はどう違うと思う？」と畳みかけるように聞いてきた。この手の数限りなくある、「理系と文系」「男と女」はどう違う？という問いには立ち入ってはいけない、というのが私の家の代々の家訓なのであるが、ここで黙りこんでいては「勝ち負け」でいうところの「負け」だと思ったのか、理系の誇りを守るべく、私の口がいきなりしゃべり出した。
 

　例えば、建築で言えば、鉄骨建築が理系で、プレハブ住宅が文系なのである。体で言えば、皮膚の感覚を大事にするのが文系で、骨から組み立てていくのが理系なのである。つまり理系は骨があるのである。そして、詩で言えば、散文詩は文系で定型詩が理系なのである。つまり、理系は型にこだわる部分があるのである。

　だから、例えば理系は女子高生の制服が大好きなのである。色々ある女子高生をセーラー服（あるいはブレザー）という記号で記号・集合論的に取り扱うことを可能にし、その記号を言葉にし、ついにはその制服を見るだけで萌えることができるのである。それが理系なのである。

　つまりは、「このアイドルがなんとなく好き」というのが曖昧模糊としたものが文系であるならば、「このアイドルがめがねっこだから好き」という確固とした意志それすなわち理系なのである。理系＝めがねっこ大好きなのである。

　と、スキーのモーグル競技でコントロールを失い、コースアウトしてしまう選手のように私の口は暴走を続け、理系＝めがねっこ大好き、という辺りではもう「勝ち負け」でいうところの「負け犬」であるようにしか思われず、理系の誇りを守るどころか、理系を単に汚しただけに終わってしまった。そこで、悔しさのあまり、今回は「めがねっこ」に対し理系的なアプローチで近づいてみることにした。そして、私が汚してしまった理系の汚名をすすぎたいと思うのである。
 

「めがねを外すと美人になる」は本当か!?

　よく、少女マンガなどで、「ヒロインが眼鏡をとると美人になった」というストーリーをみかける。今はどうだか知らないが、少なくとも昔はよくそんなストーリーを見かけた。あれは果たして本当だろうか。そして、それが本当であるならばそれは一体どんな物理現象なのだろうか？そして、ヒロインが眼鏡をとると美人になった」というストーリーと「めがねっこ大好き」というそ相反する二つの事象はどんな原因に基づいているのであろうか？それを理系的なアプローチで明らかにしてみたいと思う。
 

　めがねはもちろん視力が悪い場合に、その矯正を行うための道具である。近視の人であれば矯正のために凹レンズをかけるし、逆に遠視の人は矯正のためには凸レンズをかける。凸レンズと言えば、虫眼鏡と同じで、何かの近くにレンズを持っていけばそれが拡大されて見える。また、逆に凹レンズであれば、対象物が小さく見える。
 

凹レンズ（右）と凸レンズ（左）
凸レンズでは文字が大きく見え、凹レンズでは文字が小さく見えている

　だから、近視の人が凹レンズである眼鏡をかけた場合には、その人の目が他の人からは小さく見えてしまうのである。実世界でも、少女マンガの世界でも大きな瞳は美少女の象徴であるが、近視の人が眼鏡をかけると、大きな瞳を持つ美少女でもちっこい瞳になってしまうのである。

　試しに、仲間由紀恵に凹レンズの眼鏡をかけさせた場合の、シミュレーションを行ってみたのが下の結果である。左のめがねをかけた「近視の」仲間由紀恵は確かにキレイではあるけれど、右の仲間由紀恵の方が、美少女という魔性の魅力という点で遙かに勝っていることが判るだろう。
 

近視の場合

めがねをかけた「近視の」仲間由紀恵

めがねを外した「近視の」仲間由紀恵

　そう、近視の人の場合には、「めがねを外すと美人になる」は物理的に本当なのである。近視の人の割合は国によって大きく違うらしいが、少なくとも現代の日本では近視の人の割合は圧倒的に多い。ほとんどの人が近視である、といっても良いくらいである。ということは、そんな日本では「めがねを外すと美人になる」はかなりな確率で事実である、と言えるわけだ。
 

　それでは、「めがねを外すと美人になる」ということと相反するとしか思えない「めがねっこ大好き」現象をどう説明したら良いだろうか？一つは、遠視の場合先の近視の場合と逆のことが起きる、ということである。すなわち、遠視の人の場合には、眼鏡をかけると瞳が大きく見えるのである。すなわち、眼鏡をかければ、美少女の象徴たる大きな瞳が手に入るのである。

　下の「遠視の」仲間由紀恵の場合の眼鏡シミュレーションを見てみると、めがねをかけたことでずいぶんと美少女度がアップしていることが判ることと思う。まさに、その瞳には魔性の魅力が宿っているとしか思えないほどなのである。
 

遠視の場合

めがねをかけていない「遠視の」仲間由紀恵

めがねをかけた「遠視の」仲間由紀恵

　ということは、「眼鏡を外すと美人になる」は本当。ただし、近視の人の場合は、ということなのだ。そして、もし遠視の人であれば、「眼鏡をかけると美人になる」が本当なのである。

　とはいえ、日本人では遠視の人は少ないわけで、それではめがねっこを増やす原因たる「眼鏡をかけると美人になる」が少なくなってしまう。そこで、他の原因を考えてみると、例えば近視の人が裸眼の時には瞳の口径を小さくすることで、被写界深度を深くする、すなわちハッキリとものを見ようとして、目を細めがちであること、すなわち小さな瞳になりがちであること、なども原因の一つとして考えられるだろう。

　そしてまた、実は近視の程度が低い場合には、「めがねっこ大好き」現象を支えるもう一つの事実がある。レンズの度数がきつくなくて、他の人から見た瞳の拡大縮小が行われないような場合にも、眼鏡をかけると実は心理的に瞳の大きさが変わって見えるのである。

　下の「目が小さい」仲間由紀恵は左右で目の物理的な大きさは完全に同じである。が、心理的には結構違って見える。眼鏡をかけた仲間由紀恵の方が目が大きく見えることが判ると思う。「目が小さい」場合、めがねをかけると瞳が大きく見えるのである。
 

めがねっこチェック
「目が小さい」場合、　めがねっこの方が絶対可愛い〜。

めがねをかけていない 「目が小さい」仲間由紀恵

めがねをかけた 「目が小さい」仲間由紀恵

　日本人は目が小さい人が多いから、このような眼鏡をかけると心理的に瞳が大きく見える影響は無視できないに違いない。

　ところが、目がもともと大きい場合には、この現象はそれほど大きく現れるわけではない。もともと瞳が大きいがために、眼鏡をかけたからといって割合的にそれほど瞳が大きく強調されたりはしないのである。その例を下に示す。下の二枚は目の物理的な大きさは完全に同じなのであるが、心理的に受ける瞳の大きさ＝美少女度の違いは上の例ほどではないことが判るだろう。
 

めがねっこチェック
「目が大きい」場合　…う〜ん、あまり差がない〜。

めがねをかけていない 「目が大きい」仲間由紀恵

めがねをかけた 「目が大きい」仲間由紀恵

　ということで、

• 瞳が多きい近視の人の場合、眼鏡を外すと美少女になる
• 目が小さかったり、遠視だったりする人の場合、「めがねっこ」＝美少女になれる

などのさまざまな知見を理系的アプローチで見つけることができ、これまでの少女マンガなどに描かれたストーリー達が実は物理現象をこと細やかに描写した事実に即した観察日記であったことが明らかにされたわけである。

ところで、理系と文系…

　さて、理系的「めがねっこ大好き論」も良いのだが、話をそもそもの「どんな時に自分を理系だと思う？」という問いに戻ろう。

　よく私が見かけるパズルは大抵が論理的なパズルだ。論理的＝理系ではないから、それを理系パズルと呼ぶのはいけないと思うが、あえてそれを理系パズルと呼んでみる。間違っているのを承知で、あえてここではそう呼んでみる。

　そんな理系のパズルでもやっぱり色々あるだろう。大抵のそんなパズルの答えは答えがただ一つに限られるものだろうが、時にはその答えが無限にあるものもあるかもしれない、そして答えが一個もないパズルだってあるかもしれない。そしてまた、「答えを見つけられないこと」を証明できるようなパズルだってあるだろう。だけど、いずれにせよ、そのパズルを解く過程で現れようとする「割り切れない何か」は「それが割り切れる軸」を駆使することで、巧妙に消し去っていくことができる。だから、とてもそれは結構気持ちが良い作業だ。少なくとも、私にはそうだ。あるいは、答を判定するものが、自分ではない論理なり自然現象に任せられているから楽なのかもしれない。

　だけど、もしそんな論理的なパズルとは違う非論理的なパズル、ここではあえて文系のパズルと呼ぶようなものがあったとしたら、その答えは「割り切れない何かを拾い集めたようなもの」であるような気もする。そして、その解く過程はもしかしたら割り切れない感情や雰囲気を拾い集めて、割り切れないままに何とか答えを投げ出しいく作業であったりするのかもしれない。それに、そこでは答を判定する何かなんかそもそも存在しないか、あるいはその判定する何かが人であるのかもしれない。

　私には、そんな「割り切れないままに何とか答えを出していく作業」はちょっと辛いなぁと思う。やっぱり、私は理系パズルの方がずっと楽で気持ちが良い。だから、今度「どんな時に自分を理系だと思う？」と聞かれたら、そんなことを上手く言えたらいいな、と思う。いつも、思い浮かべたことを伝え続けたいな、と思う。

■「言葉」をあやつる魔法使い　

　今日の「わきめも」はとてもお勧め。わきさんの文章の中には、しばしば「日常生活」の中にある「不思議な異世界への入り口」が姿を現すのである。このリンクから「わきめも」に飛ばない人がいたら、それはとてももったいないので、まずはこんな一節を読んでみて欲しい。

　電車に乗っていると、女子高生達がなにやら盛り上がっている。友人やら、誰それのカレシやら、先生やらをこけおろし、最後に　　「ありえなーい」の大合唱で締めくくっている。　　「...ちゃんの化粧ってさあ、...」　　「ありえないよね」　　「ありえなーい（合唱）」　...なんとも恐ろしい会話である。すべてが却下されるのである。私は突然、彼女達に指を指され、「ありえなーい」という合唱を浴びる光景を想像した。　しかしもちろん、そんなことは起こらなかったが、ターゲットは意外なものに向けられた。電車が東小金井駅に近づくと、誰かが言った。　　「東小金井ってありえないよね。」　　「ありえなーい！（合唱）」何の理由もなく東小金井は彼女達に却下された。　電車はゆっくりとスピードを落とし、有り得ない東小金井駅に到着した。何人かの乗客が否定された街に降りていった。

　　わきさんが、いきなり理由も無く却下され存在自体を否定されなくて本当に良かったとしか言いようがないのである。そして、恐ろしい会話なのだけれど、何故かその女子高生達はとてもイキイキと色鮮やかに響いてしまうのである。さらには、否定された街に降りていく人々がまるで実体を失った影に見えてしまうから不思議なのである。


　まるで、その女子高生達が不思議な魔力を持つ魔女達で、街や人やあらゆるものから実体を抜き取り、それらのものや人をこの世から消しゴムで消していくような不思議なミステリなのである。

■アルキメデスのパンチラの式　

「スカート円錐」の明るさを探れ

「スカート円錐」の明るさを探れ

　以前、「ミニスカートの幾何学」として、女子高生の間などで流行っていたミニスカートの丈の短さの限界について考えてみたことがある。階段を上ろうとしているミニスカートを履いた女性（別に男性でも構わないが…）の下着が見えてしまうかあるいは見えないのかを、女性達が履くミニスカートの丈の長さから考察をしてみたのであった。

　その「ミニスカートの幾何学」の考察をした結果、ミニスカートの丈がちょうど32cmの時に、ミニスカートで下着が隠されはじめる境界線がちょうど階段と平行になる、ということが判ったのである。そして「下着が隠されはじめる境界線がちょうど階段と平行になる」結果、ミニスカートの丈が32cmより短いと下着が階段下を上る人達から見えてしまうようになり、逆にミニスカートが32cm以上の丈であればスカートの中の下着はなんと幸か不幸か見えることはないのだ、ということが判ったのである。ミニスカートをはいた女子高生が急な駅の階段なんかを上るときでも、ミニスカートの丈が32cm以上であれば、パンチラの恐怖に怯える必要はないということが判ったのであった。


　ところで、ミニスカートの中が見えてしまいそうになる場所というのは、必ずしも急な階段だけではないらしい。最近の東京の有名スポットなどでは、「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかがたくさんあったりするというのである。そして、そんな場所では、真上にいる「スカートを履いた女性」を急角度で仰ぎ見ることができて、スカートの中の下着がチラリと見えてしまうことがあるというのである。

　しかし、である。角度的にスカートの中の下着が見えるからといって、果たして本当に下着が見えるものなのだろうか？角度的には見えるはずでも、実際には人間の目には見えないことだってあるのではないだろうか。なぜなら、スカートが「私たちの視線から下着が見えるのを遮っている」のと同じように、スカートは「照明の光が下着にあたるのをも遮っている」のである。スカートの中というのはスカートに光が遮られて（たぶん）かなり暗いハズなのである。いや、実際に覗いてみた経験があるわけでは決してないので自信を持って「ハズ」と断言することはできないのだけれど、スカートの中が明るいわけはないと思うのである。もし、スカートの中が明るくなければ、仮にその中身を覗くことはできても結局暗くて何も見えないわけで、「スカートの中が（見えるくらいに）十分に明るいかどうか」が肝心だと思うのである。そこで、今回は「下着が角度的に見通せる条件」ではなくて、「スカートの中の下着が十分明るく見える条件」を考えてみたい。


　まずは、スカートをはいた女性を下の図のように簡単に示してみよう。スカートを下向きに開いた円錐として考えてみる。もちろん、スカートの中の下着はこの円錐の頂点に位置するわけだ。そして、スカートが広がる角度をΘとでもしてみることにしよう。その時、円錐の頂点にはどれだけの光が当たるものだろうか？

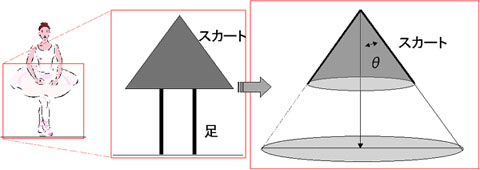　もちろん、円錐状のスカートが上からの光は遮っているわけだから、スカートの中の下着を照らす光というのは、下の床からの反射光だけである。つまりは、上の図で、「色を付けた部分の床」からの反射光のみが下着にまでたどり着き、それ以外の床からの反射光はスカートに遮られて、スカートの中を照らすことはない。ということは、「スカートの中はどれくらい明るいか？」という疑問を考えることは、それは「色を付けた部分の床からスカートの中の下着にまでたどり着く光がどれだけあるか？」ということを考えることと同じなのである。

　そしてまた、床上での光の反射に方向性が無く、光が完全に等方的に周囲に拡散するとするならば、円錐の中心（つまりはスカートの中の下着部分だ）にあたる光の量は、下の左図の色を付けた部分球の面積に比例する。つまり、「スカートの中の明るさ」は「スカートの広がり角」で決められる「部分球」の面積に比例するのである。


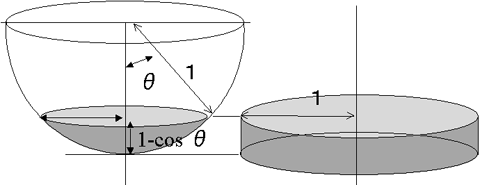　つまり、角度Θで広がるスカートの中が「どれくらい明るいか？」という疑問は、「下図で色を付けた部分球の面積はどのくらいか？」という問題に変わるわけである。「半球全体の面積に対して、スカートの広がりで決められる部分球の面積はどのくらいの割合か？」ということの答えが、それすなわち「スカートの中の明るさ」を決めているのである。

　ところで、アルキメデスが発見したように、球（もしくはその一部）の面積はその球に外接する円筒の面積に等しい。つまり、上の図の左で色を付けた部分の面積というのは、右に示したような（色を付けた）円筒の面積に等しいわけだ。ということは、右の円筒部分の面積は

円筒の面積 = 2 π (1-cosΘ)

であって、左の半球の面積が(直径=1とすると)2πだから、円錐状のスカートの中の明るさは、スカートの広がる角度をΘとするならば、「スカートの中の明るさ」は

という実に簡単な式で表されることになる。アルキメデスも、まさか自分の球と円筒の表面積に関する発見が「スカートの中の明るさを示す式（ここでは仮に『パンチラの式』とでも呼ぶことにする）」を導くために使われるとは想像だにしなかっただろうと思うが、とにかくアルキメデスのおかげで私たちはスカートの中の明るさを知ることができるのである。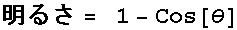

　試しに、このくアルキメデスの『パンチラの式』を使って、スカートの広がり角度Θに対して、スカートの中の明るさがどのように変化するかを計算してみると、その結果は下のグラフのようになる。このグラフは、横軸が「スカートの広がる角度」で、縦軸が「スカートの中の明るさ」を示している。周囲の「照明に照らされている床」の明るさを１とした時の「スカートの中の明るさ」を示しているのである。

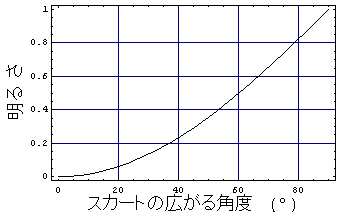　基本的にはスカートが広がるにつれて「スカートの中の明るさ」は明るくなるわけであるが、このグラフを眺めてみると、スカートの広がる角度が20°を超えるあたりから次第にスカートの中が明るくなることが判るだろう。例えば、スカートの広がる角度が30°の時には、スカートの中は「床の明るさの10%程度の明るさ」しかないが、スカートの広がる角度が60°にまで広がれば、スカートの中は「床の明るさの半分程度の明るさ」になる、ということが判るわけだ。


　ところで、人間の目というものは「見るものの明るさ」に合わせて順応する。例えば、暗いものを見るときには目の感度は自動的に上がる。だから、スカートの中がほのかでも明るかったならば（例えば床の明るさの5%程度にでも明るければ）、自動的にその明るさに目が順応してスカートの中が見えてしまうかと思いきやそうはいかない（ハズだ）。なぜなら、人間の目は明るいものを見る時には、目の感度が逆に自動的に低下してしまうからである。スカートの中以外の明るい場所（例えば照明や、照明に照らされた明るい壁）だって、自動的に視界の中に入ってくるわけで、目の感度はそういう明るい部分に自動的に合ってしまうハズなのである。

　例えば、下の画像は周りの明るさに対して、

1. 5%の明るさ
2. 10%の明るさ
3. 20%の明るさ

を持つ三種類のロゴである。この三つの画像を眺めてみれば、明るさが5%のものはなかなか判別しにくいが、20%以上の明るさのものであれば比較的容易に判別できることが判るだろう。明るいものが視野に入っている限りは、人間の目は「一番明るいものの10%以下程度の明るさのモノ」はなかなか識別することはできないのである。

5 %

10 %

20 %

　ということは、先のグラフで「スカートの中の明るさ」が10%を超えていないと、つまりは周囲にある明るい床（や照明や壁）などの明るさの10%を超えているくらいでないと、スカートの中が仮に幾何学配置的に見える条件であったとしても、実際には目の感度的にその中のようすを判別することができないに違いないのである。その場合、おそらく明るい床や壁の明るさに目の感度が合ってしまい、ほの暗いはずのスカートの中は真っ暗にしか見えず、幸か不幸かスカートの中身は識別することができないハズなのだ。

　というわけで、先ほどのグラフに「識別できる明るさか否か」を書き入れてみると、次のグラフのようになる。

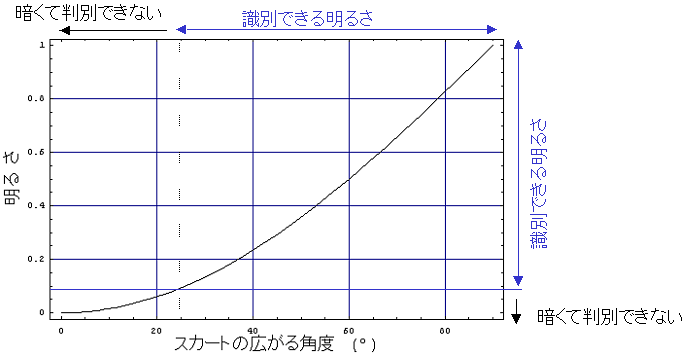　つまり、スカートの広がる角度が25-30°を超えていないと、スカートの中身は周囲の床や壁の明るさに比べて相対的に暗すぎて人間の目ではおそらく見ることができないのだ。


　例えば、スカートの広がる角度が30°以下に制限されるようなタイトスカートを穿いて、明るい壁や照明などが視界にどうしても入ってしまうような場所にたたずんでいる限りは、もし仮にスカートの中を覗かれたとしてもスカートの中は（人間の目からすると）真っ暗で何も見えないわけで、スカートの中身を見られたりするような被害にあうことはまずないだろう、ということが先のアルキメデスの『パンチラの式』から判るわけなのである。「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかであったとしても、背後に明るく輝くものがある限りには、見る人の目を眩ませることができて、スカートの中身は安全なわけである。

　ところが逆に、床が白かったりして明るいクセ（つまり下からの照明が強いクセ）に、周りに明るい壁や照明が何故かあまりないような場所がもしあったとして、もしそんな場所で（下から）スカートの中を覗かれたりしてしまうと、（下から覗く人の視界に入る）周囲の明るさに比べてスカートの中が十分明るく見えるせいで、しっかりとパンツの模様をチェックされてしまうということになるだろう、ということも予想することができてしまうのである。だから、そんな場所をもしも短いスカートをはいて歩かなければならないような場合には、例えば何かの「ピッカピッカ輝く光りモノ」でも身につけて、その光りモノの明るさを「スカートの中身をのぞこうとするスナイパー」の視界に入れて、彼らの目を眩ませてしまえば良いだろう、というアルキメデスの知恵さえ授けてくれるのだ。

　
　ところで、今回は「スカートの中の明るさを示す＝パンチラの式」を考えてみたわけであるが、この式は考えるまでもなく実にアブナイ式である。パンチラの被害防止に役に立ちそうな気もするし（全然役に立たないような気もするが）、逆に単なる「パンチラの科学」になってしまっているような気もしてしまう。「スカートの中身をのぞこうとするスナイパー」の魔の手から逃げるためのバイブルになるような気もするし、「スナイパー」のための手引き書になってしまいそうな気もする。ギリシャ神話で、あらゆる災厄が入っていたという箱がパンドラの箱だったけれど、このパンチラの式だって案外そんなパンドラの箱のような、色んな災厄の元になってしまうものかもしれないのである。しかも、パンドラの箱の場合には最後に箱の中に『希望』が残っていたわけでまだ良い（？）のである。しかし、アルキメデスの『パンチラの式』の場合には「スカートの中にだっては『希望』が入っているのだぁ」などと口に出したりしたら単に変態扱いされてしまうだけなわけで、そこはパンドラの箱よりもずっとたちが悪いのである。つまりは、科学もアルキメデスの『パンチラの式』も使う人次第なのである。

■女子高生のカーネル領域における言語的等価性　

高度に発達した離散的コミュニティでは、そこで使用される言語=表象はおよそ一般的な話し言葉とは著しく異なったものに対応させられる。本論文ではまず UNIX コミュニティにおける言語と女子高生コミュニティにおける言語の相似性を提示する。つぎにこのような言語体系をうみだす環境の認知心理学的類似性について考察し、UNIX が女子高生と数学的に等価であることを示す。また両者の今後の展開についても予測をおこなう。

　この論文で最後に行われる「女子高生との相似性から導かれるUNIXの未来予測」は「ここで我々の視界に入ってくるのは、もうひとつのビルの存在 -- つまり『池袋』である。池袋でビルといえばサンシャイン 60 であるが、サンとは高地ゲール語で『太陽』を表象し、これは UNIX 陣営における『サン』に相当する。すると池袋におけるビルというのは、その創始者であるもう一人のビルに相違ない」である。　from L.L.L@online