2000-05-12[n年前へ]
■メガネの内側にある歪み 
隠れたストレスに光を当てろ
また、可視化の話である。いや、自分でも忘れていたが、「可視化」改め「見える?見えない?」シリーズである。今回はメガネの内側にある「歪み」、隠れたストレスに光を当ててみたい。そして、そこに何があるかを見てみたいのである。
私の眼はどうも明るさに弱い。やたら太陽の光が眩しく感じることが多い。といっても、単に私のガマンが足りないだけかもしれない。あるいは、睡眠不足のせいかもしれない。そして、私は同時に暗さにも弱いのだが、こちらは単にビタミン不足による鳥目だろう。
そういうわけで、明るいのに弱いので車を運転する時には大抵サングラスをかけている。サングラスは何本も持っているわけだが、最近のお気に入りはこれである。
 |
これは、偏光フィルター機能付のサングラスである。偏光というギミック付のところがお気に入りの理由である。以前、
で書いたように、偏光フィルターがあれば色々なものの反射光のみを遮ったりすることができる。例えば、下の右側の写真では左の写真に比べてガラス表面の反射光が減少していることがわかるだろう。これは偏光フィルターの作用のせいである。 |  |
これと同じように、偏光フィルター機能付のサングラスを使えば色々な反射光を防ぐことができる。例えば、通常は反射光などで車のフロントグラスの内側にいる人の姿はよく見ることができない。しかし、このメガネをかけていれば、反射光に邪魔されずフロントグラスの内側を見通すことができるのである。もう、対向車なんてまるでフロントグラスがないかのようである。
この偏光フィルター機能付のサングラスは、通常「釣り」などで用いられるものだ。水面の反射光を防ぐことにより、水中の魚の姿などを見やすくするためのものである。結構、海の近くに住んでいる私にはうれしい機能である。
このサングラスをかけている時に、ふとある実験を思いついた。普段は透明にしか見えない「普通のメガネ」の影に隠れたストレスを目に見える形にしてみようと思ったのである。よく、「メガネの奥にストレスが隠れている」というが、そのストレスを見て取れる形にしようと思うわけだ。
そこで、新婚ホヤホヤの「夜の帝王」I田氏(関係ないが、I田氏から「Hirabayashiさん、小杉のメーリングリストで-できるかな?-の話題が出てましたよ。」と言われた時はビックリした。とりあえず、どなたか知らないが、メーリングリストで紹介して頂いた武蔵小杉勤務の方には一言お礼を言っておきたい)にメガネを借りてみた。このメガネをじっくり眺めてみてもらいたい。
 |
この透明なメガネの奥に何か見えるだろうか?そこに「歪み」は見えないだろうか?「透明だから、何も見えないだろう。」という人もいるだろうが、あるグッズを使うと、もう明らかに見えてくるのである。それが、下の写真である。レンズを固定している辺りをよく見てもらいたい。不思議な
虹模様と十字の模様が見えるはずだ。
 |
プラスチック等は製造過程での不均一な応力や、外力により複屈折性を示す。光弾性と呼ばれる現象である。そのため、偏光面を直行させた偏光フィルターの間にそういうプラスチックなどを挟みこむと、その弾性体の内部に働いている応力分布の状態を調べることができる。それを応用したのが、偏光顕微鏡などである。
例えば、下の写真はカセットテープのケースの左側部分を、偏光面を直交させた二枚の偏光フィルターで挟んでみたものである。見事に弾性体の内部に働いている応力分布が可視化できているのがわかると思う。これを応用すれば、例えば熱変形をしているようなものであれば、透明体の熱分布も簡易的に見て取ることができる。
 |
そういうわけで、先の写真あるいはそれを拡大した次の写真のように普通では見えない透明なプラスチックレンズの中に隠れている「ストレス」を見て取ることができるわけだ。
 |  |
とりとめもないが、今回は透明なメガネの影に隠れたストレスに光を当ててみた。ちゃんと見ようと思いさえすれば、目に見えるものは数多くある。「見える?見えない?」の境界線はその人自身が決めるのである。「できるかな?」では、これからも色々な「見える?見えない?」を追求し、「見えるかな?」について考えていきたいと思う。
2000-05-13[n年前へ]
■ミウラ折りの落書き紙 
思ったことを折り込めて
十年位前のことだったと思う、「知人の先生がこんなのを作ったんだけど、興味あるだろう?」と父が不思議な冊子を私にくれた。冊子と言っても、それは一枚の紙を折り畳んだ小さな小さなものだった。ちょっと面白い折り畳み方をされたその紙には、その折り畳み方の説明とその「折り畳み方」の応用が書かれていた。もちろん、その冊子の作者は宇宙科学研究所の三浦教授で、そしてその冊子の折り畳み方はあの有名な「三浦折り」である。
三浦折りの折り目を示してみると、例えば下の図のようになる。一目見てわかるように折り目が直交していない。そのため、それぞれの折り目が独立でなく、全ての折り目が同期しているのである。言い換えれば、一つの折り目を開こうとすると全ての折り目が開いていくし、一つの折り目を閉じようとすると全ての折り目が閉じていく。だから、例えば、折り目の端っこと端っこを掴んでただ引っ張れば全ての折り目が開き、そして折り目の両端を縮めれば自動的にパタパタと折り畳まれていくのである。
また、折ってみるとわかるのだが、この三浦折りは折り目が少しづつずれて重なるのである。折り目というのは厚みが他の部分に比べて厚いために、折り目が重なるとその部分だけがどうしてもかさばってしまう。しかし、この三浦折りであればそんな折り目が重ならないので、折り畳んだときにかさばらないのである。
 |
だから、太陽電池パネルなどをこんな三浦折りを使って折り畳むと、折り畳んだときにはかさばらないし、その展開や収納は隅と隅をただ引っ張ったり縮めたりしさえすれば良い、というわけで良いことずくめというわけだ。詳しくは、宇宙科学研究所のここ辺りを読んでもらうことして、参考までにそこの画像にリンクを張っておく。
 |
ところで、十年前に父からもらった「三浦折りの冊子」を捨てるはずはないから、部屋のどこかに隠れているとは思うのだけれど、何処かに隠れてしまっていて、見つけることができなかった。私の部屋が三浦折りのようになっていて、部屋の隅から隅までを全て引っ張り出すことができたら、きっとすぐにでも見つけられたのだろう。しかし、残念ながら私の部屋は三浦折りではないのである。だから、私の色々なモノや本が散らばった部屋に隠れている「三浦折りの冊子」はそう簡単に見つけられるわけもない。
そういえば、ふと何かが心に思い浮かぶことも日頃よくあることである。しかし、思い浮かんだその時に書き留めておかないと、すぐに記憶の何処かに隠れてしまって忘れてしまうことも多い。これもまた、私の記憶が三浦折りだったらよいのだろうけれど、幸か不幸か私の記憶システムは三浦折りではない。私の記憶や考えたことが三浦折りのようにパタパタ開かれていくのも見てみたい気もするけれど、隠しておきたいような夢や気持ちもあるだろうから、やはり私の記憶システムが三浦折りでない方が良いのだろう。
とはいえ、やはり後で思い出したいこともたくさんあるわけで、そんなことは思い浮かんだらすぐに何かに書き留めておかなければならないだろう。落書き帳か何かに、思い浮かんだことをすぐに書き留めておけば良いわけである。適当な落書き帳に書き留めれば、思い浮かんだことを忘れてしまっても安心である。
しかし、頭に何かが浮かぶ瞬間というのは、時間や場所を選ばないだろうから、そんな落書き帳はいつも持ち歩かなければならないだろう。となると、いつも持ち運ぶためにはコンパクトでなくてはならないし、そんな落書き帳を広げる作業は簡単に素早くできなければ不便である。だとしたら、その落書き帳はまさに三浦折りを使うべきではないだろうか? というわけで、私は自分用の「落書き紙」をミウラ折りを使って作ってみることにした。
というわけで、作ってみたのがこの「できるかな?」特製「落書き紙」である。折り畳んだ状態は三浦折り特有のちょっと不思議な重なり方になり、見た感じのデザインも割に良い感じだと思う。そして、これが「できるかな?」特製「落書き紙」折り畳みのようすである。
両端を動かすだけで、パタパタと自然に開いたり折り畳まれていくようすがよく判ると思う。 | 実際の大きさは掌にすっぽり隠れるサイズ。 裏表紙は表紙を裏返したデザイン。それは、考えたり思ったりしたことにはきっと表も裏もあるだろう、という気持ちの現れなのである。 |
ここにPDFファイル化した「できるかな?」特製「落書き紙」を置いておくので、興味のある人はぜひプリントアウトして三浦折りを実際に試してみると面白いと思う。このPDFファイルは開くときにパスワードを聞いてくるが、"hirax.net"といれてやれば開くことができる。
ちなみに、この「できるかな?」特製「落書き紙」の表と裏を見てみるとこんな感じになる。裏表紙は表紙をそのまま裏返したデザインにしてある。それは、考えたり思ったりしたことにはきっと表も裏もあるだろう、そしてそれは表裏一体で単に裏表の関係なのかもしれない、という気持ちの現れなのである。 |
 |
この「できるかな?」特製「落書き紙」の作り方であるが、まずこのPDFファイルを長手綴じで両面印刷をする。そして、上下左右マージンが不揃いであれば、端部を少し切り取る。実際に折り畳んだ後であれば、そのどの程度不揃いなのかがわかりやすいから、端部を切り取る(切り取らなくても良いが)のは一番最後でも良いだろう。
そして、表の面の折り線に沿って、次の写真のように折り畳んでいくのである。
|  |
 |  |
さて、この三浦折りの「できるかな?」特製「落書き紙」は折り畳めばとても薄く小さいから、ポケットに入れていつも持ち歩いて、心に浮かんだことなどを書きとめて持ち歩くのに最適だと思う。そして、この落書き紙の裏や表に、思ったことの表から裏までを書き留める。そして、そんな思い・考えの切り抜き・断片、を小さく折り畳んだまま伝えたい人に手渡してみて、折り畳まれたもの達がその人の掌の中でパタパタと現れてくるのも、それはそれで不思議に新鮮な感覚だろう。例えば、ちょっと不思議な「三浦折りのラブレター」なんて、不思議でいい感じだと思うんだけれど… 駄目かなぁ?
2000-11-26[n年前へ]
■ブランコの中の∞(無限大) 
なんで一体漕げるのだろう?
公園のブランコというのは、何故かとても不思議な雰囲気を持っている。ホントにうるさいくてたまらないくらいのガキんちょ達が、アクロバットのようなスゴイ技を見せていたりする。それは、まるで上海雑伎団を見ているような気分になる。小さな子がなかなかブランコが漕げず、ブランコの上で宇宙遊泳のように四苦八苦しているのを見ているのも思わず笑ってしまうくらいに可愛らしいものだ。もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。
やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう?口で上手く説明できる人がいるだろうか?
それに、そもそも私たちはブランコを何故漕ぐことができているのだろう?
いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?という手紙で始まるのは加納朋子の「ななつのこ」だが、「何故、リンゴは落ちるのかという謎」と同じく、「ブランコの漕ぎ方の謎」だってとても不思議だ。いつも目にする公園のブランコを、私たちは一体どうやって漕ぐことができているのだろう?
いつだって、どこでだって、謎はすぐ近くにあったのです。
何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。
もちろん、「何でブランコの漕ぎ方が不思議なのさ?」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。
次の図は「ブランコを漕いでる子供」である。
 |
この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか?それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。
だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか?
次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、
- ブランコの動きの中心を向いている軸A
- 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B
 |
ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。
それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。
というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。
ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか? この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか?
 |
「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ!)上がれば、ブランコの速度はもとの速度の倍になるのである!
ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。
もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ!
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。
このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、
- 初期のブランコの速度 = 10
- 重心位置を高くして 10 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- 重心位置を低くして 10 X 1/2 = 10 (何てこったい、速度が半分になっちまったか!)
- 初期のブランコの速度 = 10
- 重心位置を高くして 0 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- そのあとブランコの速度 = 0
- 重心位置を低くして 0 X 1/2 = 0 (0が0になっても全然変わってないもんね!ヘヘン!)
人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。
まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。1万円×2=二万円では1万円しかもうからないが、一千万円×2=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。
もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。
そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね!となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。
というわけで、
- ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
- ブランコが上に行ったときにその姿勢を元に戻す
それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。
というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ
- 何もしない場合
- ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
- ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合
 → ブランコの動きはず〜と変わらない |
ブランコが上にきたあたりで座り込んだ場合  → ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」 |
ブランコが上にきたあたりで立ち上がった場合  → ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」 |
この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。
ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか? それとも、ちょっと考え過ぎかな。
2002-02-20[n年前へ]
■「やおい」の評価演算子 
ベクトルの彼方で待ってて II
 東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
「福田X小泉っていうのは、結構上手くやっているのかな?」と私が言うと、おもむろに
「あれは、福田X小泉じゃなくて、絶対あれは小泉X福田なのー」とその記者が言ったのである。何を言っているのかその意味がよく判らないまま、「ん〜?」と私が首を傾げていると、繰り返し
「福田X小泉と小泉X福田は全然意味が違うのー」と言い始めるのである。何が何だか訳がわからない。じゃぁ、何か?小泉X福田だと小泉純一郎が総理大臣で福田康夫が官房長官だけど、福田X小泉だと福田康夫が総理大臣で小泉純一郎が官房長官になるとでも言うのか??政治の世界では、言う順番で総理大臣が決まるとでも言うのか?と私が口をはさむと、
「そう。ただ、ちょっと政治の世界とは違う世界かも〜。政界じゃなくて、やおい界ではー。」と言うのだ。なんだコイツ?政界は判るけど、やおい界って一体何処の世界の話だ??と、困惑する私も構わず、そこから延々と長い演説が始まった…。その大河ドラマのようにやたらと長い話を要約すると、
- やおい → 一部の女性が好む「男性同士の恋愛もののストーリー」のこと
- X → やおいの世界で恋愛の関係を示す記号。例えば、AさんとBさんが恋に落ちるであれば、Aさん×Bさんと表す。で、ここで重要なのは先に位置する方が「攻め役」となって、後に位置する方が「受け役」となる…。つまり、例えばサド侯爵とレオパルド・マゾッホであれば攻め役がサド侯爵で、受け役がマゾッホなので、サド×マゾなのである。決して、マゾ×サドではない…
で、日本酒を飲みながら、まだまだ続くその話に悪酔いしていると、「カップルの順序が重要なんだー」という言葉を聞いて、ふと中学の頃の数学の授業を思い出した。その頃、大学を出てまだ一年目の斉藤慶子似の数学の先生と話していたときに、「Hくん、あのね掛け合わせる順序が違うと結果も違っちゃう計算もあるのよ」と教わったことがあった。そんな言葉から私は未知の「数学の世界」をかいま見たりしたのである。 今考えてみれば、新任の斉藤慶子似の女性教師の個人授業なのだから、行列・ベクトルの掛け算の順序なんかじゃなくて、「もっと違う順序」を手取り足取り教えてくれても良かったんじゃないか、とか思ったりするし、そうすれば、私は未だ見ぬ「大人の世界」を覗き見ることができたのではないか、と思ったりもするのだけれど、そんなことは残念ながら無くて、私はただ「行列・ベクトルの世界」を覗いただけだったのである。
で、そんな昔話を思い出したせいか、頭の中でこんな風に思ったのである。そういえば、これまで「できるかな?」では数多く「恋の力学」でも遊んできた。ただ、そこでは「惹かれ合う恋心の大きさ」だけに注目して、そのカップルの中での役割などは考えたことがなかった。そこで、今回は「やおい」のカップルの「役割・順序」に注目し、その「役割・順序」を評価する演算子を行列・ベクトルの掛け算になぞらえながら考えてみることで、これまでと同じく色々な「恋の形」を眺めてみたいと思う。
まずは、色々な人物(実際の人物であったり、小説などの登場人物であったり)のタイプを二次元空間に配置しよう。「この人は結構攻め役が合いそう」とか「この人は絶対受け役が合うのだー」という適性を
- 攻めベクトル
- 受けベクトル
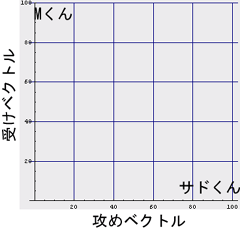 |
そして、カップリング適性では「A×B、B×Aが全然違う」ということから、外積(ベクトル積)をそのまま流用して、適当な評価関数を作ってみるのが自然だろう。まず、
カップリング適性ベクトル = (攻め度(s)、受け度(m))と表記して、例えばAさんのカップリング適性ベクトルを(As, Am)と表すことにしてみよう。すると、Aさんが「攻め」でBさんが「受け」のカップリング適性は、この二人の適性ベクトルのベクトル積として表すことができる。つまり、
A×Bのカップリング適性 = ( As * Bm - Am * Bs )となるわけである。式を眺めれば判るように、Aさんの攻め度が高くて、Bさんの受け度が高ければ、この評価関数は高い値を返す。つまり、「A×Bの順序は正しいのだー」という評価を返す。つまり、「A×B」はなかなか良いカップルだー、と教えてくれる。また、もしAさんの受け度が高くて、Bさんの攻め度が高ければ、低い値を返す。つまり、「A×Bの順序は絶対間違ってるのだー」と評価してくれるのである。なんともありがたいことに(いや別にありがたくはないか…)、この「やおいのカップリング評価演算子」が「福田X小泉」と「小泉X福田」のどちらが自然なのかを教えてくれるのだ。試しに、上のサドくんとMくんであれば、「サドくん×Mくん」= (100,0)×(0,100) = 100*100 - 0*0 = 10000でとっても「良い感じ」でああるが、「Mくん×サドくん」= (0,100)×(100,0) = 0*0 - 100*100 = -10000で「このカップリングは絶対順序が違うー」と判るわけである。
= Aさんの攻め度 * Bさんの受け度
- Aさんの受け度 * Bさんの攻め度
とりあえず、今回はこの評価演算子を作成するところまでで終えたいと思うが、いずれこの「やおいの評価演算子」を武器にして、いつか(?)「やおいの世界= やおい界」に限らず、色んな数多くの恋の関係を目に見えるようにしてみたいと思う。そして、これまで数多く考えてきた「恋の〜シリーズ」を充実させていきたいと思うのである。
ところで、今回のカップリング適性評価演算子は基本的に外積そのものである。つまり、この演算が返す値は「二人のベクトルでできる平行四辺形の面積」に等しい。つまりは、「二人のベクトルでどれだけ色んな違うことがきでるか」を示す尺度である。そして、その値は二人のベクトルが直交する時、すなわち二人のベクトルが重ならず独立である時に最大値となる。つまりは、「二人のベクトルが違えば違うほど大きく」なる。例えば、先の「サドくん×Mくん」であれば二人のS,M趣向が完全に正反対であったからとてもお似合いのカップルになったのである。
これをいわゆる恋の話で考えてみると、とっても独立な二人、趣味が重ならない二人がお似合いだということになる。なるほど、そんなカップルも世の中にはたくさんいることだろう。そんな人達を「外積タイプのカップル」と呼ぶことができると思う。
一方、趣味が重ならないカップルだけでなくて、世の中にはそれとは正反対の「趣味が重なる良いカップル」も数多くいる。それは「内積タイプのカップル」である。内積はA,Bベクトル間の正射影に比例する量であって、つまりは「二人の重なるベクトルの大きさ」である。それは例えば、相手の中に自分を重ね合わせるような「二人の重なる部分が二人を結びつけるようなカップル」なのである。
「理系と文系」・「男と女」が対極的なものでも、相反するものでもないのと同じく、「外積カップルと内積カップル」も別に二つに分けられるようなものではないだろう。「外積タイプの恋」も「内積タイプの恋」が混じり合って、それぞれに良いところもあれば、危ういところもあって、などと想像してみるのも面白いに違いない。そして、さらにはもしかしたらベクトル空間で萌えることができるようになったりするかもしれない。
そういえば、ふと考えてみると以前「恋の形を見た人は」で最後に引用した本橋馨子の「兼次おじ様シリーズ」は男性同士の恋の話だった。つまりは「やおい」の話だった。そこで、もう一度そのセリフを最後に飾って眺めてみようと思うのである。
「愛はどんな形をしているか知っているか?」「見た事ないからわかりません。」「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...
もし愛に優劣を決めるものがあればなんだろう?... 異性愛か、同性愛か、そんなものじゃない …たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」
2004-04-05[n年前へ]
■今日の「山田くん、座布団一枚」:「萌え」価が負=「萎え」!? 
「萌え」と「燃え」の概念は直交しているのであって、萌え価が負というのはすなわち「萎え」ではないかと思われる。(中略) 萌えと燃えが直交する概念なのだから、仮定されているエレガントな萌えこそが「燃え」にほかならない。これは、燃えに燃えが重ねられると暑苦しくて萎える、というオタクの心理構造をよく現している。という「萌え」価が負=「萎え」という考え方。「萌え」の対局が「萎え」なのか、それとも「萌え」と「萎え」は違う関係なのか、謎は深まりヲタク度はさらに高まる。

