1999-12-21[n年前へ]
■恋の力学 
恋の無限摂動
クリスマスが近くなると、街のイルミネーションが綺麗に輝き始める。いかにも、ラブストーリーが似合う季節である。そこで、今回は、"Powerof love"、すなわち、「恋の力」について考えてみたいと思う。「恋の力」により、人がどのような力を受け、人がどう束縛されるのか、などについて考えみたいのである。また、恋に落ちたカップルがどのような行動をするのかについて解析を行ってみたい。
「できるかな?」では以前、
において、カップルが他のカップルを意識する力について考えたことがある。カップル同士の間に働く斥力を考えることにより、鴨川カップルの行動を考えてみた。それと同様に、今回はひとつのカップルのみを考え、その中に働く力を考えてみるのである。ひとつのカップルの「男」と「女」の間にどのような力が働くかを考えるのである。そういうわけで、今回の登場人物は「男」と「女」である。その二人は「恋に落ちた二人」である。二人の間には「恋の力」が働いているのだ。その二人の間に働く「恋の力」について考察することにより、恋に落ちたカップルの行動について考察を行ってみることにする。
といっても、「恋の力」を精密に測定した報告例は未だ存在しないので、ここでは適当な値を用いていくことにする。「恋は距離に負けない」とか「遠くて近きは男女の仲」などとははよく言われる。そこで、距離によらないと近似した。また、「遠くて近きは男女の仲」の意味を考えれば、恋の力は無限遠まで働く力である、と考えるのが自然である。
そこで、今回の「恋の力」は距離に関わらず一定であると仮定した。距離=rとした時に-r/Abs[r]の大きさで「相手に惹かれる」ものとした。仮に第一種「恋の力」(仮称)とでもしておく。
今回は「恋の力」は距離によらないものとした。しかし実際は、(通所の距離においては)「男」と「女」は距離が近いほど惹かれ合うし、離れてしまうと惹かれ合う力は弱くなるというのが自然であると思われる。そこで今回の第一種「恋の力」(仮称)は、あくまで大雑把な近似ということにしておく。
恋する二人の間に働く力をもう少し正確に記述しておくと、
- 「恋の力」 = - 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「恋の力」=優柔不断度 * 「恋の加速度」
であることだ。心がトキメいてもなかなか行動を起こすことが出来ない人がいるだろう。そういう人は「優柔不断度」が高いというわけである。恋の行動における慣性を示すパラメータである。
また、今回は空間を1次元であると簡略化してみた。1次元の空間の中で「男」と「女」が動き回るのである。その時間的変化を調べてみるのだ。従って、シミュレーション結果は空間軸が一次元+時間軸一次元で、合わせて2次元となる。
さて、この「恋の運動方程式」を解くことにより、恋する二人の行動は予測することが可能となるわけだ。試しに、その計算サンプルを示してみる。なお、今回は時間方向で数値的に逐次解を求めている。
初期状態は
- 「男」位置=5, 速度=0,魅力=100,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
位置や時間の単位は任意単位である。「0」と「5」は東京と大阪であっても良いし、ロンドンとニューヨークであっても良い。あるいは、実空間でなく精神的な空間と考えてもらっても構わない。すなわち、心の動きを示しているものとするのである。
また、二人の「魅力」や「優柔不断度」は対等である場合だ。その結果を下に示す。このグラフは縦軸が空間位置であり、横軸が時間である。黒線が「男」であり、赤線が「女」である。
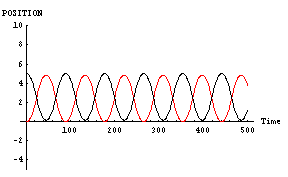 |
「男」と「女」が同じように相手の方向へ向かっているのがわかると思う。これが「恋の無限摂動」である。こういった「恋の無限摂動」の代表的なものには「君の名は」の主人公達の動きなどがある。恋に落ちた二人が、延々とすれ違いを続ける物語である。これは、この「男」と「女」の行動そのものである。
この計算結果では「男」と「女」が糸を紡いでいるようにうまく絡みあっているのがわかる。「恋の無限摂動」の幸せなパターン例である。これは、「男」と「女」が対等であったことがその一因である。
その証拠に、「男」と「女」が対等でない場合の計算結果を示してみる。次に示すのは、
- 「男」位置=5, 速度=0,魅力=10,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
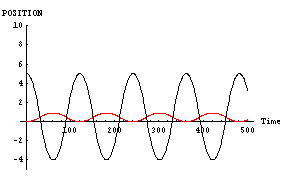 |
「男」が右往左往するのに対して、「女」はほとんど動いていないのがわかると思う。おそらく、この場合には「男」と「女」の「心」もこれと同様のパターンを示しているものと思われる。すなわち、「男」の「心」は揺れ動いているのに対し、「女」の「心」はほとんど動いていないのである。
先の例と異なり、これは実に不幸な計算例である。不幸ではあるが実際によくある例であると思う。以降、これを「男はつらいよ」パターンと呼ぶことにする。「女」に「男」が振り回されているパターンだ。もし、奇跡的に結婚などしても、将来どうなるかは火を見るより明らかである。
それでは、「男」と「女」の「魅力」が同等で、かつ、とてもスゴイ場合を示してみる。すなわち、ドラマの主人公達のようにとてつもなく魅力的な二人が恋に落ちた場合である。一般人とは違う二人が恋に落ちたら、果たしてどのような行動を示すのであろうか?この場合のパラメータは以下に示す、
- 「男」位置=5, 速度=0,魅力=1000,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=1000,優柔不断度=10
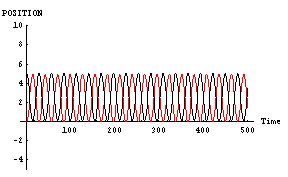 |
「魅力ある二人が恋に落ちた場合には、あまり近づかない方が良い」という教訓をここから得ることができる。
最後に、「男」と「女」の二人ともにあまり魅力がない場合である。パラメータとしては、
- 「男」位置=5, 速度=0,魅力=2,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=2,優柔不断度=10
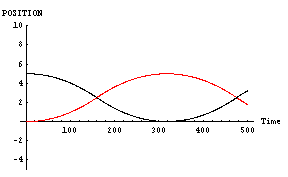 |
これなど「恋」と言えるのかどうかもわからない位である。ほとんど、「ただすれ違っただけの相手」である。これがさらに進むと、魅力がお互いに0同士のパターン、
- 「男」位置=5, 速度=0,魅力=0,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=0,優柔不断度=10
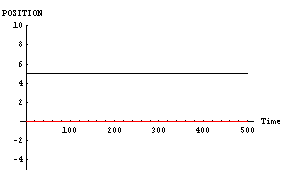 |
これっぽっちも「男」と「女」は「恋」に落ちていないのである。これではカップルの「男」と「女」ではなく、単なる他人である。
さて、今回は行わなかったが、カップルに「恋のエネルギー損失」を導入することにより、「恋の無限摂動」を減衰させることができる。それにより、現実のカップルの行動にさらに近づくことができるのではないかと、私は考える。何らかの抵抗が生じることにより、「恋の無限摂動」が減衰するのだ。そして、二人は接近した状態で停止するわけだ。
さて、今回の登場人物は「男」と「女」だけであった。しかし、現実でも、ドラマの中でも、通常は多くの登場人物が登場する。登場人物が「男」と「女」だけというような理想的な条件のみではない。
人の恋路を邪魔する(主人公からすれば)ヤツも必ず登場する。また、特定の登場人物の間では斥力が働くだろう。そのような場合、一体どのような現象が生じるのだろうか。
そもそも、今回の恋する二人の行動パターンは予測可能であったが、現実そのようなことがあるだろうか?果たして、未来の行動パターンは予測可能なのだろうか?色々な登場人物が現れる場合にも、今回の結論は成立するのだろうか?
それらは次回の課題にしておく。題して、「恋の力学 三角関係編- 恋の三体問題- (仮称)」である。「恋の力」を一般化し、多体問題として解いてみたいのである。恋する人達とその周りの人達がどのような行動をするか、恋の三角関係においてどのような力が働いているのか、について解析を行ってみたい。今回は、そのための前準備というわけである。
1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
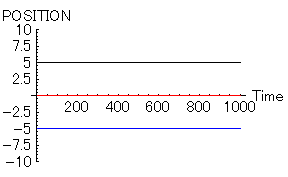 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
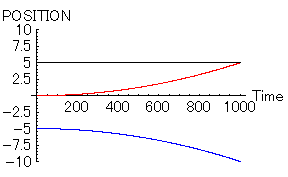 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
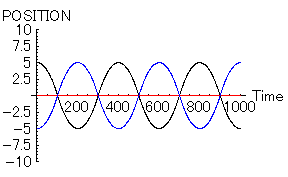 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
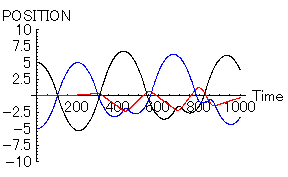 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)
2000-02-05[n年前へ]
■恋の固体物理学 前書き編 
シリコン・エイジの恋
これまで、様々な「恋の形」について考えてきた。古くは、
であったり、あるいは、であったりした。最近の「恋の力学」シリーズでは、初めに男と女の間の「恋の二体問題」を考え、そして二人の男と一人の女の間の「恋の三体問題」を考えてきた。しかし、それらの「恋の力学」が取り扱ってきたものは、ごく少数の登場人物により演じられる物語を解析したものである。また、特に「男」と「女」の間に性質的な差がないものとして、解析を行ってきた。
このような解析の前提条件、
- ごく少数の登場人物
- 「男」と「女」の間に性質的な差がない
- 数え切れない多数の人物が登場し
- 「男」と「女」の性質の間に差がある
例えば、
- 「男」も「女」も結構人数はいるのであるが、その数がかなり違う。
- 「男」が諸星あたるのように、やたら行動力があるが、「女」の方ははなかなか動かない
- 恋人達に何かのショックを与えると分かれてしまう。
- その場の雰囲気でカップルになっちゃった
こういった色々なことが「恋の物理学」では起きる。しかし、
で書いたように、夏目漱石の時代に作り上げられた「恋の力学」ではそのような現象の解明は困難である。そこで、新たな「恋の科学」の分野を作り上げ、そういうことについて考えを巡らせていきたい、と思う。とはいえ、いきなりやるのは私には難しい。そこで、まずは解析のための準備をしていきたい。
というわけで、本シリーズは題して、「恋の固体物理学」である。先に述べたような「不均等な恋の挙動」を例えば半導体工学のような固体物理学のテクニックを用いて解明したいと思うのだ。割に単純な「恋の力学」シリーズとは別に、「恋の固体物理学」シリーズを始めたいと思うのである。
普通に考えるならば、 - 何故「恋」の挙動解明に、半導体工学? - と思われるかもしれない。確かに、唐突であるとは思う。しかし、考えてみればそれほど不自然ではない。何しろ、現在はシリコンの時代であると言われる。
プラスティック・エイジを経て、現在はシリコン・エイジが世界を支配している。シリコン= 半導体技術により、世界は動いているのだ。そうであるなら、「恋に動かされる人」の挙動も、、半導体技術を用いることにより解き明かすことができるかもしれない。(いや、もちろん今考えた理屈である。簡単に言えば、こじつけである。)
そしてまた、「恋」は一般的に(例外はあるが)
- 男
- 女
- プラスの「正孔(ホール)」
- マイナスの「電子(エレクトロン)」
- 「男」も「女」も人数はいるが、その数がかなり違う。
そのような理屈で半導体工学と関連づけながら、「恋の固体物理学」について考えてみたいと思う。
このシリーズは少しヘビー(私にとって)なので、今回は前書きのみに留めたい。これから公開予定の作品群を紹介すると、
- 恋の固体物理学 恋のバンドギャップ編 - 彼女の防護壁を突破しろ! - (仮称)
- 恋の固体物理学 恋のドーピング編 - 女子校の教師はパラダイスか? - (仮称)
- 恋の固体物理学 恋の熱励起編 - 別れたくなかったら頭を冷やせ - (仮称)
- 恋の固体物理学 恋のp-n接合編 - 一方通行の恋の行方 - (仮称)
- 恋の固体物理学 恋のEinsteinの関係式編 - 本気と浮気の境界線 - (仮称)
まだまだ続く「恋の力学」シリーズと共に「恋の科学」を作り上げていきたいと思う。
2000-02-27[n年前へ]
■「文学論」と光学系 
漱石の面白さ
前回、
でさて、モナリザと言うと、夏目漱石と「モナリサ」にも言及しなければならないだろう。と書いた。何しろ
- 恋の力学 三角関係編 - 恋の三体問題 - (1999.12.27)
- 草迷宮・空間'99 - ネコの目から見た世界- (1999.11.05)
- 「こころ」の中の「どうして?」-漱石の中の謎とその終焉 - (1999.09.10)
- 夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
- [Scraps]人静月同照 - ぼくらが旅に出る理由- (1999.06.17)
その漱石は「永日小品(リンク先は青空文庫)」(リンク先は青空文庫)の「モナリサ」中で
「モナリサの唇には女性(にょしょう)の謎(なぞ)がある。原始以降この謎を描き得たものはダ・ヴィンチだけである。この謎を解き得たものは一人もない。」と書いている。女性には興味がなかったとも言われ、ずっと付き添っていた男性との関係も噂されるダ・ヴィンチである。ここらへんは、果たしてどうか?とも思う。むしろ、新宿のホストクラブのホストの方が女性(にょしょう)の謎(なぞ)については詳しいのではないかとも私は考えたりもする。
が、そんなことはどうでも良い。漱石はレオナルド・ダ・ビンチのモナリザに興味を持ち、小品を書き上げたのである。そこで、漱石とダ・ヴィンチの相似点を考えてみたい。
レオナルド・ダ・ビンチの著作には「文学論」というものがある。漱石にも同じ名前の「文学論」がある。この「文学論」はこれまで読んだことがなかったのだが、
- 「漱石の美術愛」推理ノート 新関公子 平凡社 ISBN4-582-82927-9
- 遠近法
- 漱石の文学論の「公式」
これが、とても面白い。仮名遣いが古いため、なかなか目に入ってこないのであるが、とても面白い。これは絶対に文庫本にすべきである。眺めているだけでも面白い。
まずは、冒頭のフレーズがいきなりこうである。
およそ文学的内容の形式は(F+f)なることを要す。Fは焦点的印象又は観念を意味し、fはこれに付着する情緒を意味す。まるで、理系の教科書である。そして、目次(編)を大雑把にさらってみる。
- 文学的内容の分類
- 文学的内容の数量的変化
- 文学的内容の特質
- 文学的内容の相互関係
- 集合的F
また、「文学論」中では、例えば、浪漫派と写実派の違いについて数値的な比較を通じて述べられていたりする。実に「科学的」な思考による「文学論」である。いや本当に漱石は凄い。
さて、中の文章を解説する力は私にはない。そこで、中の図表を示してみることにする。そこで適当に思うことなどを書いてみようと思う。
次に示すのは、「文学論」の冒頭の方で「意識の焦点・波形」を説明した図である。
 漱石全集第十一巻より |
この図は人間が何かを感じるときには焦点にピークがある、そして、その周りはぼやけたものが連続的に続いているということを示したものだ。これなど、
の時の「恋のインパルス応答」を彷彿とさせる。あの時の「恋のインパルス応答」を次に示してみる。 |  |
この意識される恋心(f)は先の「意識の波形」と全く同じである。ある出来事(F)と、それに付着する情緒(f)を示したものとなるわけだ。付着する情緒(f)というのは中心が一番大きく、その周りにぼやけたものが繋がっているというわけである。人間の感じ方・情緒を光学系と結びつけているわけだ。
いやはや、「恋のインパルス応答」と同じようなことを考える人はやはりいるものである。まさかそれが漱石だとは思いもしなかった。しかも時代を考えると凄まじい、としか言いようがない。
そして、さらに次に示すのは
およそ文学的内容の形式は(F+f)なることを要す。Fは焦点的印象又は観念を意味し、fはこれに付着する情緒を意味す。ということを示す図である。先の - 「漱石の美術愛」推理ノート - ではこの図と遠近法の関連が述べられている。
 漱石全集第十一巻より |
ここで、縦軸は「時間」となっており、横軸は「色々な出来事」である。ある人が感じた「色々な出来事」を時間方向に収斂させていくと、そこには「作者自身の視点がある」というわけだ。これが漱石の言う「文学論」の中心である。
この図などカメラや望遠鏡の光学系を彷彿とさせる。「光学系の一例」を以下に示す。
 |
先の「文学の焦点」を示した図はレンズで光を焦点に集めるのと全く同じだ。いや、「焦点から光を投光する」のと同じと言った方が良いだろうか。以前、
で、景色に焦点を合わせて、フィルムに結像させるのがカメラだ。しかし、フィルムに写っているのは単なる景色ではない。カメラの光が集まる焦点にフィルムが位置していると思い込むとわからなくなる。逆から考えてみれば簡単に判るはずだ。カメラの視点にフィルムが位置しているのだ。フィルムに景色が写っているのではなく、フィルムが景色を選び、景色を切り取っているのである。と書いたのと全く同じである。その光学系には歪みもあるかもしれないし、色フィルターもかかっているかもしれない。しかし、とにかく焦点にはその人自身がいるのである。写真に写っているのは、撮影者の視点なのである。写真を見れば、撮影者が、どこに立ち、何を見てるかが浮かび上がってくるはずである。フィルムに写っているのは撮影者自身なのだ。
写真でも文章でもとにかく何であっても、色々感じたことを表現していく時、その焦点には表現者自身がいる。私の大好きなこの2000/2/25の日記なんか、実にそれを感じるのである。
2000-04-01[n年前へ]
■恋の力学 恋の相関分析編 
「明暗」の登場人物達の行方
「恋の力学」シリーズである。前書き編が登場したきりで、なかなか本編に入らない「恋の固体物理学」シリーズではない。今回は、
の続き、ということになる。以前、
の中で書いたように、恋の力学シリーズは夏目漱石の影響を多大に受けている。そして、同様に夏目漱石の影響を受けているシリーズがある。それは「文章構造可視化シリーズ」である。何しろ、「文章構造可視化シリーズ」は夏目漱石をきっかけとして、始まっているのである。また、シリーズの中の話を見ればわかるように、
- 夏目漱石は温泉がお好き?- 文章構造を可視化するソフトをつくる - (1999.07.14)
- 失楽園殺人事件の犯人を探せ- 文章構造可視化ソフトのバグを取れ - (1999.07.22)
- 「こころ」の中の「どうして?」 -漱石の中の謎とその終焉 - (1999.09.10)
- 「星の王子さま」の秘密- 水が意味するもの - (1999.11.15)
そのための準備として、まずは「文章構造可視化シリーズ」で作成した"wordfreq"をバージョンアップしてみた。その動作画面を以下に示す。
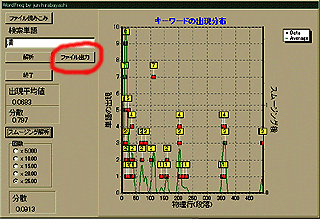 |
赤丸で示したボタンに「ファイル出力」と書いてあるのがわかると思う。つまり、文章中に「任意の単語」が出現した出現頻度を解析した結果をファイル出力する機能を持たせたのだ。1段落中に「任意の単語」が出現した数をテキスト形式で出力するようにしてある。このファイル出力結果を他のソフトに読み込めば、色々な解析ができるわけだ。いつものように、このソフトはここ
においておく。言うまでもないが、アルファ版の中のアルファ版だ。さて、今回用いるテキストは
でも登場した「明暗」である。そこで、「青空文庫」から「明暗」の電子テキストをダウンロードした。そして、バージョンアップした"wordfreq"で- 津田
- お延
- 清子
- 吉川
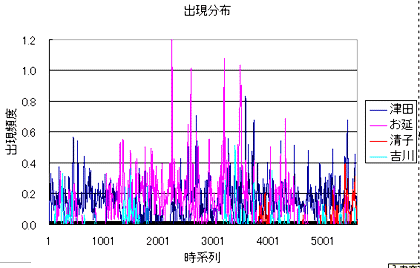 |
しかし、これだけでは、よくわからない。せいぜい「清子」が小説の後半(といっても、未完であるが)に登場しているなぁ、という位だろう。しかし、さらに解析を加えてみると、もう少し面白いことがわかる。
今回は、これらの登場人物間のお互いの関わりを調べたいのである。であるならば、これらの「登場人物」の出現分布の間の相関を調べてみると面白いだろう。互いの関係を示す「相関」を調べてみるのである。異なる「登場人物」が同じような出現をしているならば、それは無関係ではない。きっと、その登場人物の間には何らかの関係があるに違いないのだ。
そこで、「明暗」を時系列的に6つの部分に分けて、津田と他の登場人物の出現分布間の相関を調べてみたのが次のグラフである。
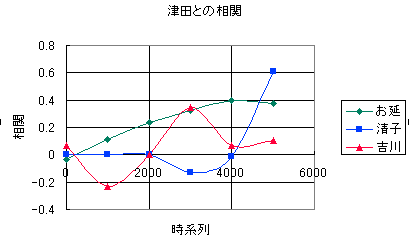 |
このグラフでは、横軸が時系列であり、縦軸が相関を示している。縦軸で上になればなるほど相関が高い、すなわち、「関係がある」のだ。「相関」は本人の場合で「1」である。だから、例えば最後の部分の清子の「0.6」という結果は関係がアリアリということを示しているわけだ。
また、「清子」と「吉川(ここでは夫人を意図している)」の相関が逆であることが面白いだろう。「吉川」が活躍(暗躍?)した後に、「清子」が登場するわけだ。
そして、この「明暗」が盛り上がっていくようすすら、見えてはこないだろうか?全く血の通っていないPCが解析した結果が、漱石の描こうとした「こころ」の動きを読みとっているような気が(少しは)しはしないだろうか?そして、このグラフの延長線上に、漱石の描くはずだった、「明暗」の結末はあるはずなのだ。
さて、このグラフを見ていると、
で計算した恋の多体(三体)問題の計算結果を思い出してしまう。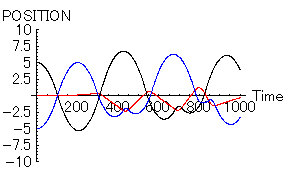 |
漱石は、きっと恋の三体問題を意識しながら「明暗」を書いたのである。だから、ある意味当然なのではあるが、科学と文学の一体化した世界が感じられ、とても面白い気分である。さて、この解析結果を元にして、まだまだ色々とやってみたのであるが、それは次回である。