1999-02-28[n年前へ]
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
 |  |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
 |  |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 |  1階微分 |
 13/10 (=1.3)階微分 |  15/10 (=1.5)階微分 |  17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
1999-05-30[n年前へ]
■パーマンのパラドックス 
ボトルネックは何処だ?!
以前、
ハードディスクのエントロピーは増大するか?- デフラグと突然変異の共通点 - (1999.03.28)
の最後に「突然変異(あるいは、ハードディスクで言えばデフラグメント)のような現象が起きて、エントロピーが減少しない限り、熱的死(いや企業や会社であれば画一化、平凡化、そして、衰退だろうか)を迎えてしまうのだろう。」と書いた時に少し不思議な感じがした。それは、次のような矛盾を感じたのである。
まずは、
- 何事につけても、全体としての強さは一番弱いところで決まってしまう。
- 全体としての完成度を高くするためには、どこの強さも同じであるのが理想的である。
- 従って、全体を構成する部分というものは均質であるのが理想的である。
もし、ビルの鉄骨の一部に弱い所があれば、そこから崩壊が始まり、いずれビルが崩壊することは免れないだろう。
精度・力が高い所がいくらあろうと、「一番精度・力が低い所の=全体の精度・力」なのである。従って、一番精度・力が低い所を改良するのが全体としての完成度を高めるための唯一の方法である。
これは、モノであろうが、個人であろうが、グループであろうが同じである。例えば、写真を撮って出力することを考えよう。いくら写真の素材が良くてもカメラマンの腕が悪ければ駄目であるし、写真自体が良くても、写真の出力装置が悪ければ、それもやはり駄目である。そもそも、カメラマンが狙う被写体自体が悪ければ、答えはやはり同じである。
従って、精度・力を揃えた均質的な状態でなければ良いものは生まれないわけである。
これと、先の「画一化、平凡化、そして、衰退」すなわち、「画一化は良くない」ということの間に矛盾を感じたわけである。
しかし、少し考えてみると特に矛盾が無いことがわかる。ロボットを作る場合を考える。
- まずは一人で機械系も電気系もソフト部分も自分で作っていた。
- ソフト部分がどうも苦手なので、ソフトが得意な友達に手伝ってもらう。
- すると、電気系が比較的うまく行かないようだ。
- そこで、友達の友達に電気系を手伝ってもらう。
- それぞれ得意な部分で力を発揮し、特に弱いところもなくなった。
- ロボットの完成だ。
それでは、数学的にふざけたことを考えてみる。といっても、難しく考えるのではなく、中学生でも知っていそうなあの式を使うのである。
簡単の為にX,Y二つの部品からなるものを考える。それらの単独での精度(あるいは、出力)をx,yとすれば、全体としての精度(あるいは、出力)を考えると、それは(x* y)^(1/2)と置くのが自然だろう。それぞれ単独であれば、単なる和としては(x + y)/2であるわけである。ここで、2で割ったり1/2乗しているのは規格化しているようなものである(あとの落ちに繋げるためでもあるのだが...)。
今やりたいことは、(x * y)^(1/2)がなるべく大きくなるようにしたいのである。というわけで、相加相乗平均の関係式の登場である。
| x->(0,50),y->(0,50)の範囲で図示したもの | |
| (x+y)/2 ...相加 |  |
| (x * y)^(1/2) ...相乗 |  |
| (x * y)^(1/2)-(x + y)/2 ...相乗-相加 |  |

すなわち、x=yの時に(x * y)^(1/2)は最大になるわけである。良く知られている、相加相乗平均の関係式である。今回の話では、それぞれの精度・力が均質であれば理想的というのはこういったことである。異なる分野・方法で力を発揮しという方は簡単だ。異なる分野・方法で力を発揮するのでなければ、わざわざ乗算、すなわち、いっしょに組ませる必要がない。
さて、タイトルの「パーマンのパラドクス」であるが、少々疲れてきたので、本題は次回にしたい。今回はタイトルについての考察を上の話に絡めてしてみるに留める。
私は「パーマン」についてほとんど知識がない。TVアニメを観ていた記憶がある位である。だから、パーマンの名前の由来が何であるか知らない。スーパーマン+罰としての「パー」からきているのかもしれないが、ここで勝手な想像をしてみる。英語で考えてみると、par=同等、同水準、平均であるから、par-manは「平凡な主人公ががんばってスーパーマンになる」という気持ちが込められているのかもしれない。これはありそうな話である。
ここで、「平均」でなくて同等というような意味をそこに入れたらどうなるだろうか?パーマン1,2,3,4号に対して、par=同等、同水準、平均というような視点から考えてみるのである。あるいは、パーマンだけではなく、他で考えたらどうだろうか....
1999-08-09[n年前へ]
■色を伝える時に、考え忘れていたこと(色弱と色空間 その1) 
We can work it out!
オプトニューズ (1999) No.4の光の話題に三楽病院の岡島修氏が「レーザポインタと色覚異常」という小文を書いている。色弱の人の感じ方とプレゼンテーション(特にレーザポインタの色)に関する提言である。それを読んであることを思い出した。何年か前、Labofinder(Macintoshを科学分野で使うユーザーグループ)でプレゼンテーションについて特集していた発表会だったと思う。どなたかが発表を行った後に、次のような質問があった。
「私は色弱なのですが、プレゼンテーションを行う際に使う色などについて、そのような人を意識して作成されているでしょうか?」
恥ずかしいことに、私はあまり考えたことがなかった。そして、本WEBを作るに際してもそういった点はおろそかになっていると思う。そういう自分自身への反省を込めて、色弱と色空間について考えてみたいと思う。
まずは、色弱に関する情報を調べよう。
- COLOR HANDICAP( http://www.sakuranet.or.jp/~tks/color/text/ )
- からーふぃくしょん( http://sun.endless.ne.jp/users/tanafic/ )
- Dr.MeMeの おめめ講座 (http://www.so-net.ne.jp/vivre/eye/ )
それでは、私なりの理解と考察を始めてみたい。
目に映る明るさって何ですか? - 君は天然色- (1999.07.05)
の回で触れたが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。この内、色(すなわち光の波長方向に関する感じ方)を感じるのは、錐体の働きによるものである。錐体には3種類有り、
- L錐体 -> 赤
- M錐 -> 緑
- S錐体 -> 青
目に映る明るさって何ですか? - 君は天然色- (1999.07.05)
を参照のこと)。それらの錐体に異常がある時に、色弱もしくは色盲が発生する。
| L錐体 (赤) | M錐体 | S錐体 | 先天性色覚異常の分類 |
| O | O | O | 正常 |
| X | X | X | 桿体1色覚 (全色盲) |
| O | X | X | 錐体1色覚 (赤) |
| X | O | X | 錐体1色覚 (緑) |
| X | X | O | 錐体1色覚 (青) |
| X | O | O | 第1色盲 (赤色盲) |
| O | X | O | 第2色盲 (緑色盲) |
| O | O | X | 第3色盲 (青色盲) |
| OX | O | O | 第1色弱 (赤色弱) |
| O | OX | O | 第2色弱 (緑色弱) |
| O | O | OX | 第3色弱 (青色弱) |
この図中でOは正常、Xは欠損、OXは機能低下である。
M,L錐体に関する異常はX染色体劣勢遺伝をする。また、錐体1色覚、および、S錐体に異常がある第3色盲・第3色弱は比較的少ないという。
それでは、これらの錐体に異常があるとどのような色を識別できなくなるのだろうか? 私は先に挙げたようなWEBを読んだくらいの知識がないので、数学的な考察をおこなってみる。現実をよく知らないため、実際の症例とはかなりの違いがあるかもしれない、ということは先に断っておく。
現実の症例の参考としては、岡島修氏の「レーザポインタと色覚異常」中に挙げられているCIEXYZ表色系における強度色覚異常者(第1異常、および、第2異常)の混同色を用いる。その図を加工し、XY色度図を重ねたものを以下に示す。それぞれの図において、白い直線上の色を混同してしまうのである。
 |  |
今回は、通常の(Red,Green,Blue)データを基本として考える。PCなどで表示を行う際に一番よく使うからである。任意のRGBデータをCIEXYZ表色系に直すためには、
WEBページは会社の顔色 -WEBページの色空間を考える2- (1999.04.26)
で用いたハイビジョンTVの色空間を例に用いて、
- X= 0.412391R + 0.357584G + 0.180481B
- Y= 0.212639R + 0.715169G + 0.072192B
- Z= 0.019331R + 0.119195G + 0.950532B
- x=X/(X+Y+Z)
- y=Y/(X+Y+Z)
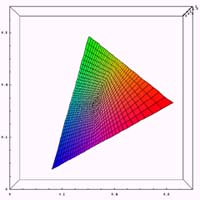
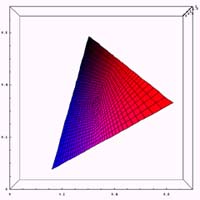
それでは、通常、第1色盲(赤色盲)、第2色盲(緑色盲)の3種類についてxy色度図の計算例を示してみる。ある錐体に異常が存在する場合に、どのような色空間が再現されるかの計算を行ってみる。通常のxy色度の位置において、ある錐体の刺激を無くした場合に色がどう変化するかを示したものである。であるから、第1色盲(赤色盲)、第2色盲(緑色盲)においては通常使われるxy色度図とは異なるものになる。また、ここで示した色が色弱の人が見ている色という意味でもない。
単純に、ある錐体が得るであろう情報を無くしたときに、情報の識別がどのように困難になるかを確認した、と言った方がいいかもしれない。
また、本来3錐体の波長感度特性はRed,Green,Blueの単波長というわけでもない。しかし、今回は簡単のために、3錐体の波長感度特性はRed,Green,Blueの単波長であるという仮定の元に計算を行っている。そのため、かなり現実とは違う結果になっている。近々、きちんとした計算をするつもりである。
 |  |  |
ここでは、Z方向(明るさ方向)に対して無視を行っているので、かなりの誤差が存在すると思う。また、計算の中で一つの錐体に異常があるときの、RGBデータの再配分を計算する部分に極めて大雑把な近似をおこなっているので、その部分でも誤差が大きいと思う。
また、Red,Green,Blueの三色により色空間を形成しているため、各点を頂点とする三角形内に色空間は収まることになる。
この計算結果を眺めながら、岡島修氏の「レーザポインタと色覚異常」中に記述されている色弱における混同しやすい色の例、
- 第1色盲
- 赤と黒
- ピンクと青
- 第2色盲
- 赤と緑
- オレンジと黄緑
- 緑と茶
- 青と紫
- ピンクと白
- 緑と灰色
例えば、通常の色空間において赤(すなわち右上)の場所を第1色盲の色空間の中で見て欲しい。黒との識別が困難なのは一目瞭然だろう。また、下の図に示すように、通常の色空間でピンク(1)と青(2)が第1色盲の色空間の中でどうなっているかを見れば、
 | 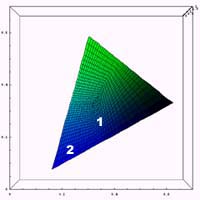 |
これも1と2の識別が困難であることが容易に想像がつく。第2色盲でも同じように見てみて確認して欲しい。
なお、上の図中で中心部が暗くなっているが、それはグリッド線のためであり、本来の色はもっと白っぽい色である。また、今回は岡島修氏の「レーザポインタと色覚異常」中の図と比較するために、CIExy色度図を用いたが、もともとxy色度図は人間の感じ方とは結びつけにくい。いずれ、均等色空間における解析を行うつもりである。また、先に記述したようにきちんと錐体の波長感度特性を考慮に入れた計算をするつもりである。今回はあくまでごく簡単な実験である。
というわけで、今回は色弱の方がどのような色空間を感じているかを考察してみた。今回の話中には色々間違いもあると思う。なにか訂正すべき情報を見つけてくださったら、教えて欲しい。
画像出力に携わる方でこのWEBをご覧になっている人もいるはずだ。色を正しく伝えることを日夜考えている人もいるだろう。しかし、色を正しく伝えることを考えるときに、考え忘れていることはないだろうか? 「正しい伝え方」は、誰にとって「正しい」のだろうか?私達が当然のように感じている色についても、異なる感じ方をする人のことを考え忘れてはいないだろうか?
そういった人は少数だと言われる方もいるかもしれない。しかし、あなたが当然の権利のように享受しているものは果たして全ての人が得ているものだろうか? もしかしたら、その権利を享受している人の方が少数派であるものもあるのではないだろうか?
やることは至極簡単なことだ。技術的に言うならば、人の知覚も「デバイスの一部」として考えた際に、「人の知覚」が数種類あるものとして、異なるデバイス間のカラーマッチングを考えれば良いだけのことだ。もちろん、一筋縄ではいかないだろうが、得られるものの大きさからしたら、やってみる価値はあるだろう。
プレゼンテーションソフト、あるいは数多くのソフトウェアにそういったことをきちんと考えたテンプレートが現れ、WEBサイトの色、画像機器のカラーマネジメントにそういった「全ての人(健常者と呼ばれる人のモデルだけでない)の感じ方まで含めたカラーマッチング」が適用されていく日も必ず来るはずだ。もしかしたら、このWEBサイトに来ている人の中には、今すぐにでもそういうことを始めることが出来る人もいるかと思う。果たして、そんなことが「できるかな?」と思われる人もいるかもしれないが、きっとできる筈だ。
こういったことは色覚に限る話ではないと思う。考え忘れていることは数多くある。できることも数多くある、と私は思う。
2000-05-17[n年前へ]
■恋の形を見た人は 
恋の相対性理論
さて、前回
では、三人の登場人物A子 : 「瞬間」的に燃え上がるタイプの女の人達の間で繰りひろげられる色々な「出来事・きっかけ」と、それにより発生する「恋する心」を「恋のインパルス応答」を用いて計算してみた。その結果、C男とB子がカップルになれば「ほのぼの」とした幸せな生活をしそうだ、というところまで考察した。
B子 : 「ゆっくり」燃えるタイプの女の人
C男 : いつも、とっても良い男
今回は、その三人に加えて
- D男 : ほとんどの場合、悪い男
さて、今回登場する「D男 = ほとんどの場合、悪い男」はかなり酷い男である。D男がA子とB子に対して何をしたか時系列を追ってみてみることにしよう。
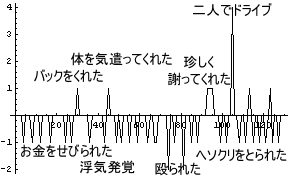 |
- お金をせびり、
- 浮気をするし、
- それを追求すると殴る蹴るの暴行を働き、
- せっせと貯めたヘソクリを奪いパチンコに行ってしまう、
それに対して、前回のC男は次のグラフのように悪いことは何一つしない良い男だ。
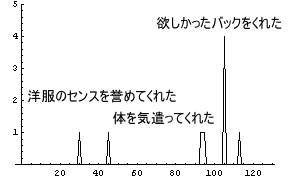 |
悪いことは何一つしない。良いことばかりをしてくれるのである。何とも良い人である。普通に考えれば、女の人の「ハート」はC男ががっちり掴み、D男は警察官にでもがっちり掴まれているのが当然であろう。掴まれたが最後、シャバには二度と出てきてこないで欲しい位である。しかし、そう単純な話ではないのだ。
人の感覚には「順応」というものがある。簡単に言えば「慣れ」である。ひどいことしかしない男と普段接していると、それが当たり前に思えてしまうのである。相対化してしまうのだ。普段のD男に対する印象が「当たり前」に思えてしまうのである。
さて、その「恋する心」の「順応」を計算するにはどうしたら良いだろうか?そう、普段の印象を基準にすれば良いのだ。普段の印象、すなわち「印象の平均値」を「恋する心」から引けば良いのである。例えば、A子のC男に対する「恋する心」を計算してみることにする。次のグラフで黒字が「色々な出来事」と「恋のインパルス応答」の畳み込みであり、本来のあるべき「恋する心」である。そして、緑字が環境順応後、すなわち、本来のあるべき「恋する心」から「印象の平均値」を引いた「恋する心」である。
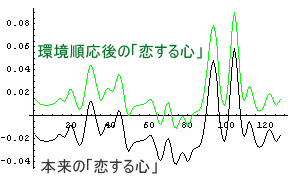 |
この図で、環境順応後の「恋する心」が本来の「恋する心」よりいい印象であることがわかると思う。何故かというと、環境に順応するということは普段の印象が当たり前の状態と思ってしまうことである。普段「悪い」男を相手にする場合は、「悪い」のが当たり前だと思ってしまうのである。数学的には、「悪い」のを引くのであるから、「マイナスを引くとプラスになる」のと同じである。それを式で表してみると、
環境順応後の「恋する心」 = 本来の「恋する心」 - 普段の態度
なのであるから、普段の行動が極めて悪いD男の場合は
環境順応後の「恋する心」 = 本来の「恋する心」 - ( 悪い印象)ここで「悪い印象」が「良い印象」の反対であることから、( 悪い印象 ) =( -良い印象 )とおくと、
環境順応後の「恋する心」 = 本来の「恋する心」 - ( -良い印象)であるから、
環境順応後の「恋する心」 = 本来の「恋する心」 + ( 良い印象)となる。なんと、「悪い印象」が「良い印象」にすり替わるのである。恐るべし、「環境順応」である。スイカに塩をかけると、ショッパイどころか逆に甘く感じられるのと同じく、ひどいD男がちょっとでも良いことをすると、「ものすごく良いこと」に感じられてしまうのである。前回、
「恋の印象の平均化効果」というものを武器に、「辛(つらい)」が「幸(幸せ)」にすりかわる様子を見てみることにしたい。「辛(つらい)」が「幸(幸せ)」は紙一重なのだ。「辛(つらい)」は「幸(幸せ)」で、「幸(幸せ)」は「辛(つらい)」なのである。と書いたが、これがそうだ。普段の「辛(つらい)」を引くと、マイナスをマイナスすることでプラスに変わり、「辛(つらい)」が「幸(幸せ)」にすりかわるのである。
そして、普段悪いことをしないC男の場合はこれとまったく逆に、普段の良い印象を引いてしまうが故に、環境順応後の「恋する心」には「悪い印象」が加わってしまうのである。「普段良い男」が少しでも悪いことをすると、散々に悪く言われてしまうのと同じである。
さて、こういった環境順応した状態での、A子のC男に対する「恋する心」とD男に対する「恋する心」を眺めてみることにしよう。次のグラフは黒字がA子のC男に対する「恋する心」を示し、緑字がA子のD男に対する「恋する心」を示している。
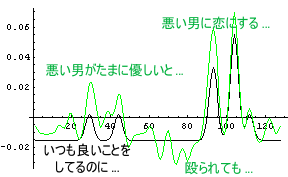 |
なんと、A子は普段悪いD男の方に強い「恋する心」を感じてしまうのである。「おいおい、それでいいのか?」、と言いたくなるような状況である。「オマエはマゾか!?」と、つい言ってしまいそうである。
まぁ、じっくり物を考えないA子はおておいて、それではB子はどうだろうか?きっと、C男と上手くいくだろうB子はどうだろうか?もちろん、「人の良い」C男を選んでくれるだろう。というわけで、次のグラフが、A子とB子のD男に対する「恋する心」を比較したものである。緑字がA子のD男に対する「恋する心」を示し、黒字がB子のそれを示している。
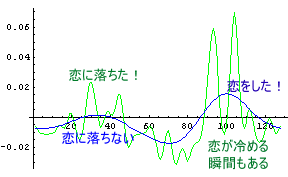 |
何ということだろう。こともあろうに、B子もD男に恋をしてしまうのだ。哀しいかな、C男は失恋してしまうのである。しかも、こtもあろうにD男にである。なんということだ!もちろん、D男がB子にひどいことをした時、すなわち「B子のD男に対する恋する心」が低下した時にA子とD男が別れるという可能性もある。しかし、残念ながらB子は「ゆっくり」タイプなのである。A子と違って、「すごく恋が冷める瞬間」がないのである。A子の場合はとっさのいきおいでD男と別れるという可能性もあるが、B子の場合はむしろD男にひっかかりやすいと言えるかもしれない。
このようにして、「普段は悪い男がたまに優しいことをすると、女の人はふと恋に落ちてしまう」という恐怖のストーリーがいたるところで発生するのである。
私の楽しみ「ちゃろん日記」の2000/03/09の「わしはダメだった」に、「印象の平均化定理」に関するしみじみとした一節があるので、そのまま引用してみたい。
「下僕(仮名)は、不幸な女がどぅやってできるか知っとるか?」「一般相対性理論」によれば、完全なる時空間の基準がない。それと全く同じように、絶対的な幸せの基準など存在しない。本人がそれでいいと言うなら、それでいいのかもしれない。強引を承知で言うならば、それが「恋の相対性理論」である。恋の座標軸は本人が決めるしかないのである。「・・・う?ん」「不幸な女は、フダンはとんでもない男がたま?にほんのすこしだけ見せる優しさが忘れられないコトにより生産される」「・・・・・・」「母ちゃんがそぅだった、こりからもそりは生産されるだろうしそんな女が絶えるコトはないだろう、でもそりでいいのカモ知れんの、本人がそりで幸せだったのなら」
さて、これまで、「できるかな?では何度も「恋のかたち」を何とか目に見える形にしようとしてきた。きっと、それはこれからも変わらないだろう。とりあえず今回の話は、私の好きな本橋馨子の「兼次おじ様シリーズ」の中のセリフを引用して、締めくくることにしたい。
「なぁ兼次、愛はどんな形をしているか知っているか?」
「見た事ないからわかりません。」
「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...」
「もし愛に優劣を決めるものがあればなんだろう?... たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」
2000-06-24[n年前へ]
■「色っぽい声」の秘密 
キャバクラ嬢は英語が上手い!?
以前、
で私は鈴が鳴るような綺麗な声がとても好きなのである。いつか、そういう声の秘密について調べてみたい、と思う。と書いた。今回は「男を惑わす魔性の声」について考えてみたい。
「男を惑わす魔性の声」といっても色々ある。私の場合、「鈴が鳴るような声」も好きだし、森本レオの声も大好きである。両極端であるが、本当なのだからしょうがない。それは他の人も同じで、その人ごとに好きな声と言うのは違うはずだ。などと言い出すと、どんな声が「魔性の声」なのかわからなくなる。そこで、「魔性の声」を出すプロに注目してみよう。「男を惑わすプロ」の出す声に注目してみるわけだ。
「男を惑わすプロ」と言えば、例えばキャバクラそれともキャバレー?(どちらも、残念ながら行ったことないけど)で男性を手玉にとるキャバクラ嬢ははずせないだろう。彼女らの声はまさに「魔性の声」としか、言いようがない(行ったことないから、想像で書いてるけど)。例えば、
「あァ〜ン、もう社長さんたらァ。」の「ァ〜」の部分なんて、どうだ。これぞ、まさに「男を惑わす魔性の声」だという気がしないだろうか。この声に惑わされて、路頭に迷った彷徨える(エロ)子羊達の数は数え切れないはずである(多分)。今回はこの「色っぽい声」の秘密に迫ってみようと思う。
↑ココ
さて、、まずはデータ収集が必要である。何より一番良いのは本物のデータを手に入れることである。すなわち、夜のキャバクラへ出撃するのが一番良いわけだ。私も「データの精度」にこだわる意味でも、ぜひそうしてみたい。使命感すらあると言ってもいいくらいである。しかし、残念ながら諸事情がそれを許さないのである。
そこで、infoseekで「色っぽい声」で検索をかけて見つかった高等遊民氏のVOICE.WAVを使ってみることにした。聞いてみればわかると思うが、この色っぽい声は先の「ァ〜」と同じような種類の声なのである。
今回はこの声に注目してみることにしよう。次に示すのが、高等遊民氏の「色っぽい声」中で解析を行った部分である。
 |
その部分を拡大してみると次のような音声波形である。この音声波形に「色っぽい声」の秘密が隠されているのである。
 |
さて、この音声波形に不思議なところはあるだろうか?「色っぽい声」の秘密の鍵となるところはないだろうか?そう考えながら、この音声波形を眺めていると不思議なことに気づいた。
果たして、これは「あ」と言って良いのだろうか?これが「あ」であるという思い込みを私はしていたのではないだろうか?今回、一番最初に
例えば、次に私の声で「あ、え、お」を示してみよう。上の魔性の声「あァ〜」は下の波形で言えば、むしろ「お」とか「え」に近いのがわかるはずだ。
 え  お  |
もちろん、別人の声であるから音声波形が異なるのは当たり前だろう。そこで、フォルマントを調べてみることにした。それが下のグラフである。赤丸部分が「あァ〜ン」の秘密を解くポジションである。「あァ〜ン」のフォルマントと日本語の母音がどういう位置にあるかを表示したものである。
 |
何と、そもそも日本語にはこの「色っぽい声 = 魔性の声」「あァ〜ン」を示すべき音がないのである。日本語にとってこの「色っぽい声= 魔性の声」は未知の音なのである。
考えてみれば、それはそうかもしれない。人間誰しもよくわからないものには「恐れ」と同時に「好奇心」を刺激される。例えば、異性というよくわからないものに惹かれる気持ちだってその一例だろう。だから、少なくとも日本人にとっての未知の音であるものが「色っぽい声= 魔性の声」に感じられるようになったのは、ある意味当然と言えるのではないだろうか?
「男を惑わすプロ」であるキャバクラ嬢が日本語の音の領域図を知った上で、この「色っぽい声= 魔性の声」「あァ〜ン」を発しているとは私も考えないが、少なくとも日本語の音の分布からすれば、「まさに男を惑わすツボを抑えている」ことがわかる。恐るべし、キャバクラ嬢である。
日本語の母音だけではなんなので、英語の母音の領域も参考までにこれに重ねてみよう。それが下の図である。
 |
なんと、英語ではこの領域は「未体験ゾーン」ではないのである。「色っぽい声= 魔性の声」「あァ〜ン」の音は発音記号で言うとVの上下がひっくり返ったやつの領域に重なってしまうのだ。英語圏の人にとってはこの「あァ〜ン」は未体験の音ではないのである。私は英語の発音は涙が出るほど、上手くできないのであるが、もしかしたら「魔性の女性」達にとってはいともたやすくその発音ができるのかもしれない。
ところで、先程の「知らない音 = 魔性の声」理論からすれば、英語圏の人にとってはこの「あァ〜ン」はそれほど「色っぽい声」ではないということになりそうだが、残念なことに私は生粋の日本人なのでそれを確かめることはできない。それに調べたら、きっとこの「知らない音 = 魔性の声」理論は崩壊してしまうだろう。
さて、最後に色っぽそうな音を数学的に合成してみた。
あなたの感性が豊かであるか、想像力が豊かであれば、このいかにも人工的な音の中のにも「色っぽい声= 魔性の声」「あァ〜ン」のエッセンスが感じられ、心惹かれるはずである。今回は簡単にやっただけなので、この音の内容については詳しく説明はしない。次回(いつものごとく何時になるかは全然わからないが)、
- Mathematicaで「あァ〜ン」- 色っぽい声を合成しよう - (仮題)