2000-11-13[n年前へ]
■WEBサイトでMONOPOLY 
これも一つのリンクページ
先日、ZDNet Japanを眺めていると面白い記事があった。ボードゲームの「モノポリー」にドットコム版ができたというのである。
- 「モノポリー」にドットコム版( http://www.zdnet.co.jp/news/0011/06/monopoly.html )
- Monopoly ( http://www.monopoly.com/dotcom/dotcom.html)
ところで、「モノポリー」というのは実に酷なゲームである。お金を奪い合い、お金が無くなったプレイヤーは容赦なく破産させられるのである。金が乏しくなってきて、もう他人に払うお金の持ち合わせなんか全然無くて「オレは別にここでこのままじっとしていたいんだぁ。」と言っても、そんなことは許されず強制的にサイコロを振らされるのである。そして、勝手に旅をさせられてわけのわからない場所に移動させられたかと思うと、「あっ、そこオレの場所。ホテルがあるから300ドル払ってね。」となるのだ。オレはただこの道ばたでじっとしていたいだけなのに、何でサイコロを振らされて、しかもオマエのホテルに泊まらアカンねん!と泣き叫びたくなるのである。オレは金なんか持ってないから、そんなグルグル高そうな場所を旅する余裕なんかないの!と言っても他人はただ笑うのみなのだ。
ヒドイ話である。ほとんど、「金なんか別にいらないよ。」と言っているのに勝手に金を貸して、しかもバブルが崩壊したら強引に金を取り立てはじめるどこぞの国の銀行のノリである。
「7並べ」くらいでも泣く子供(それは昔の私。親戚が集まるとよくこの話になり、今でも泣きたくなる。)もいるというのに、「モノポリー」なんかやった日にはもう子供が人間不信になることは間違いない。ハッキリ言って、「モノポリー」で涙をこぼして写真を撮られた大学生を私は何人も知っている。イナかっぺ大将の「風大左エ門」のように両目からボヨ〜んと涙をこぼす大学生の写真だって私の手元にはあるくらいだ。
そう言う感じで「モノポリー」はあまりにも子供達には酷なゲームなので、純粋で(少なくとも勝負には)可哀想な子供達と「モノポリー」をやるときには、銀行係になった私はいつも救済のためのお金をばらまいてしまう。つまり、お金が無くなりそうな子供が出そうになると、「日本銀行から、ボウナスが出たぞぉ!」と言いながら、みんなにお金をバラまいてしまうのである。確かに、泣きそうな子供はいなくなるではあるが、何故かそのあとオソロシイほどのインフレが襲ってくるのである。先ほど、どこぞの国の銀行に皮肉を書いてしまったが、少なくとも、私にはツブれそうな会社にお金をバラまくどこぞの国の大蔵省を怒る資格は無さそうである。子供達と「モノポリー」をやるときには、私も全く同じコトをしているのである。
ところで、「モノポリー = MONOPOLY」はといえば市場(ゲーム上では場所だけど)独占をして、お金をもうけるゲームである。WEBサイトの世界でも同じように「独占」という状況はあって、
で書いたように、「インターネットのほとんどのアクセスというものは、ごく少数の特定のサイトへのもの」なのである。ごく少数の大手サイトによってほとんどのアクセス数は独占されているのである。まだ普通の商売であれば独占禁止法( Antitrust [Antimonopoly] Law)があるのだが、WEBサイトへのアクセスではそんな独占禁止法なんかあるわけがない。なので、WEBサイトを冠するドットコム企業の独占を狙う「モノポリー」ドットコム版というのはとても当たり前で自然なのである。
というわけで、「モノポリー」ドットコム版を私はとても面白く感じたので、そのHIRAX.NETEditionを作ってみることにした。つまりは、ただの私のリンクページなのであるがまぁちょっとデザイン的に変わっていて面白いのと思うのは私だけだろうか?
 |
それでは、振り出しからこれらのサイト達の紹介をしていきたいと思う。まずは、WEBでショッピングをしよう。というわけで、ぷらっとホームと秋月電子通商である。ここで電子部品や面白グッズ・ソフトを揃えたら、お次は私の巡回コースの基本である技術系サイトである。今日の必ずトクする一言・Fast& First・突撃実験室と廻ってみよう。
さて、牢獄を眺めながら次は情報サイトを廻ってみよう。というわけで、お笑いパソコン日誌・MAQ?MAK?MAC!・ZDNetNEWSだ。最後のヤツだけ個人サイトではないが、今回の情報源でもあるし一応入れてみた。
そして、お次は続・技術系(LabVIEW・電子工作編)というわけで、LabVIEWinfo sharing・えるむ・CyberWorkShopである。最初のは同業ライバル社の方というところに親近感を持っていたりするのだ。CyberWorkShopはもう永久に更新が無さそうなところがとても残念である。
そして、パーキングを経由して「読み物サイト」へ行こう。寂しいことに更新が停止したままのちゃろん日記(仮)・もう本気で感情移入せざるを得ない我妻との闘争・そしてこの我妻サイトの弟子サイトでもある乳から息子に宛てた手紙である。
そして、次は「理系文系ごっちゃまぜ読み物」である。まずは、本来こんなところに登場する資格はないのだが、本人のサイトということで強引に登場させた「できるかな?」・「僕が作る僕の可能性」という言葉も私は大好きなボクテレビ・そして、トンデモ系の推理を作るのは大変だろうなぁとつくづく思わざるをえないHMRだ。
そして、最後のコーナーを曲がって次は時事エッセイ日記だ。まずは、ワイドショーの奴隷・麗美のぷらぷら日記である。理系風ワイドショーという感じが面白いところである。そして、何故か場所の関係でここに配置されたデザインの一つの理想たるげんれい工房・言霊参上(ことだまさんじょう)だ。
そして、最後の二つ、つまりゲームの「モノポリー」で言えばここに止まったら大変だぁ、という場所はもちろんWEB噂の真相と2ちゃんねるである。ここで自分と関係する情報などを見かけてしまうと、実際の所結構ビックリするものである。
もちろん、私の巡回サイトといいうのはここに挙げたものだけでなくて、こっそり覗いているサイトは多々あるわけだ。しかし、そういうところはとりあえず、秘密である。
さて、本当の「モノポリー」ならともかく、今回のWEBサイト達はいくら泊まろうがお金を取られたりはしない。もちろん、一部のサイトでは広告くらいは表示されるかもしれないが、間違っても「あっ、ここオレのサイト。ドメイン維持のために300ドル払ってね。」ということはないハズである。だけど、時間だけはタップリ奪われてしまうかもしれないから、そのつもりで。
2001-05-16[n年前へ]
2001-06-28[n年前へ]
■今日のモザイク 
今日の研究者からのメール。「やり方次第では「この先」も望めそうなのですが、根っから文系の私には理詰めで考えていく余地が残されておらず、ここが限界でした。また何よりも作業途中で、モザイクがかかった状態の画像を「縮小すると、なんだかすごくよく見える」ということに気づいてしまい、制作意欲をごっそりと剥がれたという理由もあるのですが……。」とのこと。リンク先はあくまで18禁です。ハイ、絶対に18禁です。(リンク)
2002-02-11[n年前へ]
■めがねっこ大好き。 
めがねを外すと美人になるは本当か!?
理系=めがねっこ大好き? 「どんな時に自分を理系だと思う?」と文系人間に聞かれた。私は「うむむ…」と答えに詰まってしまった。そんな私に、その文系人間はまるで勝ち誇ったような表情で「じゃぁ、理系と文系はどう違うと思う?」と畳みかけるように聞いてきた。この手の数限りなくある、「理系と文系」「男と女」はどう違う?という問いには立ち入ってはいけない、というのが私の家の代々の家訓なのであるが、ここで黙りこんでいては「勝ち負け」でいうところの「負け」だと思ったのか、理系の誇りを守るべく、私の口がいきなりしゃべり出した。
例えば、建築で言えば、鉄骨建築が理系で、プレハブ住宅が文系なのである。体で言えば、皮膚の感覚を大事にするのが文系で、骨から組み立てていくのが理系なのである。つまり理系は骨があるのである。そして、詩で言えば、散文詩は文系で定型詩が理系なのである。つまり、理系は型にこだわる部分があるのである。と、スキーのモーグル競技でコントロールを失い、コースアウトしてしまう選手のように私の口は暴走を続け、理系=めがねっこ大好き、という辺りではもう「勝ち負け」でいうところの「負け犬」であるようにしか思われず、理系の誇りを守るどころか、理系を単に汚しただけに終わってしまった。そこで、悔しさのあまり、今回は「めがねっこ」に対し理系的なアプローチで近づいてみることにした。そして、私が汚してしまった理系の汚名をすすぎたいと思うのである。だから、例えば理系は女子高生の制服が大好きなのである。色々ある女子高生をセーラー服(あるいはブレザー)という記号で記号・集合論的に取り扱うことを可能にし、その記号を言葉にし、ついにはその制服を見るだけで萌えることができるのである。それが理系なのである。
つまりは、「このアイドルがなんとなく好き」というのが曖昧模糊としたものが文系であるならば、「このアイドルがめがねっこだから好き」という確固とした意志それすなわち理系なのである。理系=めがねっこ大好きなのである。
「めがねを外すと美人になる」は本当か!?
よく、少女マンガなどで、「ヒロインが眼鏡をとると美人になった」というストーリーをみかける。今はどうだか知らないが、少なくとも昔はよくそんなストーリーを見かけた。あれは果たして本当だろうか。そして、それが本当であるならばそれは一体どんな物理現象なのだろうか?そして、ヒロインが眼鏡をとると美人になった」というストーリーと「めがねっこ大好き」というそ相反する二つの事象はどんな原因に基づいているのであろうか?それを理系的なアプローチで明らかにしてみたいと思う。
めがねはもちろん視力が悪い場合に、その矯正を行うための道具である。近視の人であれば矯正のために凹レンズをかけるし、逆に遠視の人は矯正のためには凸レンズをかける。凸レンズと言えば、虫眼鏡と同じで、何かの近くにレンズを持っていけばそれが拡大されて見える。また、逆に凹レンズであれば、対象物が小さく見える。
 |
だから、近視の人が凹レンズである眼鏡をかけた場合には、その人の目が他の人からは小さく見えてしまうのである。実世界でも、少女マンガの世界でも大きな瞳は美少女の象徴であるが、近視の人が眼鏡をかけると、大きな瞳を持つ美少女でもちっこい瞳になってしまうのである。
試しに、仲間由紀恵に凹レンズの眼鏡をかけさせた場合の、シミュレーションを行ってみたのが下の結果である。左のめがねをかけた「近視の」仲間由紀恵は確かにキレイではあるけれど、右の仲間由紀恵の方が、美少女という魔性の魅力という点で遙かに勝っていることが判るだろう。
 |  |
そう、近視の人の場合には、「めがねを外すと美人になる」は物理的に本当なのである。近視の人の割合は国によって大きく違うらしいが、少なくとも現代の日本では近視の人の割合は圧倒的に多い。ほとんどの人が近視である、といっても良いくらいである。ということは、そんな日本では「めがねを外すと美人になる」はかなりな確率で事実である、と言えるわけだ。
それでは、「めがねを外すと美人になる」ということと相反するとしか思えない「めがねっこ大好き」現象をどう説明したら良いだろうか?一つは、遠視の場合先の近視の場合と逆のことが起きる、ということである。すなわち、遠視の人の場合には、眼鏡をかけると瞳が大きく見えるのである。すなわち、眼鏡をかければ、美少女の象徴たる大きな瞳が手に入るのである。
下の「遠視の」仲間由紀恵の場合の眼鏡シミュレーションを見てみると、めがねをかけたことでずいぶんと美少女度がアップしていることが判ることと思う。まさに、その瞳には魔性の魅力が宿っているとしか思えないほどなのである。
 |  |
ということは、「眼鏡を外すと美人になる」は本当。ただし、近視の人の場合は、ということなのだ。そして、もし遠視の人であれば、「眼鏡をかけると美人になる」が本当なのである。
とはいえ、日本人では遠視の人は少ないわけで、それではめがねっこを増やす原因たる「眼鏡をかけると美人になる」が少なくなってしまう。そこで、他の原因を考えてみると、例えば近視の人が裸眼の時には瞳の口径を小さくすることで、被写界深度を深くする、すなわちハッキリとものを見ようとして、目を細めがちであること、すなわち小さな瞳になりがちであること、なども原因の一つとして考えられるだろう。
そしてまた、実は近視の程度が低い場合には、「めがねっこ大好き」現象を支えるもう一つの事実がある。レンズの度数がきつくなくて、他の人から見た瞳の拡大縮小が行われないような場合にも、眼鏡をかけると実は心理的に瞳の大きさが変わって見えるのである。
下の「目が小さい」仲間由紀恵は左右で目の物理的な大きさは完全に同じである。が、心理的には結構違って見える。眼鏡をかけた仲間由紀恵の方が目が大きく見えることが判ると思う。「目が小さい」場合、めがねをかけると瞳が大きく見えるのである。
「目が小さい」仲間由紀恵  | 「目が小さい」仲間由紀恵  |
日本人は目が小さい人が多いから、このような眼鏡をかけると心理的に瞳が大きく見える影響は無視できないに違いない。
ところが、目がもともと大きい場合には、この現象はそれほど大きく現れるわけではない。もともと瞳が大きいがために、眼鏡をかけたからといって割合的にそれほど瞳が大きく強調されたりはしないのである。その例を下に示す。下の二枚は目の物理的な大きさは完全に同じなのであるが、心理的に受ける瞳の大きさ=美少女度の違いは上の例ほどではないことが判るだろう。
「目が大きい」仲間由紀恵  | 「目が大きい」仲間由紀恵  |
ということで、
- 瞳が多きい近視の人の場合、眼鏡を外すと美少女になる
- 目が小さかったり、遠視だったりする人の場合、「めがねっこ」=美少女になれる
ところで、理系と文系…
さて、理系的「めがねっこ大好き論」も良いのだが、話をそもそもの「どんな時に自分を理系だと思う?」という問いに戻ろう。
よく私が見かけるパズルは大抵が論理的なパズルだ。論理的=理系ではないから、それを理系パズルと呼ぶのはいけないと思うが、あえてそれを理系パズルと呼んでみる。間違っているのを承知で、あえてここではそう呼んでみる。
そんな理系のパズルでもやっぱり色々あるだろう。大抵のそんなパズルの答えは答えがただ一つに限られるものだろうが、時にはその答えが無限にあるものもあるかもしれない、そして答えが一個もないパズルだってあるかもしれない。そしてまた、「答えを見つけられないこと」を証明できるようなパズルだってあるだろう。だけど、いずれにせよ、そのパズルを解く過程で現れようとする「割り切れない何か」は「それが割り切れる軸」を駆使することで、巧妙に消し去っていくことができる。だから、とてもそれは結構気持ちが良い作業だ。少なくとも、私にはそうだ。あるいは、答を判定するものが、自分ではない論理なり自然現象に任せられているから楽なのかもしれない。
だけど、もしそんな論理的なパズルとは違う非論理的なパズル、ここではあえて文系のパズルと呼ぶようなものがあったとしたら、その答えは「割り切れない何かを拾い集めたようなもの」であるような気もする。そして、その解く過程はもしかしたら割り切れない感情や雰囲気を拾い集めて、割り切れないままに何とか答えを投げ出しいく作業であったりするのかもしれない。それに、そこでは答を判定する何かなんかそもそも存在しないか、あるいはその判定する何かが人であるのかもしれない。
私には、そんな「割り切れないままに何とか答えを出していく作業」はちょっと辛いなぁと思う。やっぱり、私は理系パズルの方がずっと楽で気持ちが良い。だから、今度「どんな時に自分を理系だと思う?」と聞かれたら、そんなことを上手く言えたらいいな、と思う。いつも、思い浮かべたことを伝え続けたいな、と思う。
2002-02-20[n年前へ]
■「やおい」の評価演算子 
ベクトルの彼方で待ってて II
 東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
「福田X小泉っていうのは、結構上手くやっているのかな?」と私が言うと、おもむろに
「あれは、福田X小泉じゃなくて、絶対あれは小泉X福田なのー」とその記者が言ったのである。何を言っているのかその意味がよく判らないまま、「ん〜?」と私が首を傾げていると、繰り返し
「福田X小泉と小泉X福田は全然意味が違うのー」と言い始めるのである。何が何だか訳がわからない。じゃぁ、何か?小泉X福田だと小泉純一郎が総理大臣で福田康夫が官房長官だけど、福田X小泉だと福田康夫が総理大臣で小泉純一郎が官房長官になるとでも言うのか??政治の世界では、言う順番で総理大臣が決まるとでも言うのか?と私が口をはさむと、
「そう。ただ、ちょっと政治の世界とは違う世界かも〜。政界じゃなくて、やおい界ではー。」と言うのだ。なんだコイツ?政界は判るけど、やおい界って一体何処の世界の話だ??と、困惑する私も構わず、そこから延々と長い演説が始まった…。その大河ドラマのようにやたらと長い話を要約すると、
- やおい → 一部の女性が好む「男性同士の恋愛もののストーリー」のこと
- X → やおいの世界で恋愛の関係を示す記号。例えば、AさんとBさんが恋に落ちるであれば、Aさん×Bさんと表す。で、ここで重要なのは先に位置する方が「攻め役」となって、後に位置する方が「受け役」となる…。つまり、例えばサド侯爵とレオパルド・マゾッホであれば攻め役がサド侯爵で、受け役がマゾッホなので、サド×マゾなのである。決して、マゾ×サドではない…
で、日本酒を飲みながら、まだまだ続くその話に悪酔いしていると、「カップルの順序が重要なんだー」という言葉を聞いて、ふと中学の頃の数学の授業を思い出した。その頃、大学を出てまだ一年目の斉藤慶子似の数学の先生と話していたときに、「Hくん、あのね掛け合わせる順序が違うと結果も違っちゃう計算もあるのよ」と教わったことがあった。そんな言葉から私は未知の「数学の世界」をかいま見たりしたのである。 今考えてみれば、新任の斉藤慶子似の女性教師の個人授業なのだから、行列・ベクトルの掛け算の順序なんかじゃなくて、「もっと違う順序」を手取り足取り教えてくれても良かったんじゃないか、とか思ったりするし、そうすれば、私は未だ見ぬ「大人の世界」を覗き見ることができたのではないか、と思ったりもするのだけれど、そんなことは残念ながら無くて、私はただ「行列・ベクトルの世界」を覗いただけだったのである。
で、そんな昔話を思い出したせいか、頭の中でこんな風に思ったのである。そういえば、これまで「できるかな?」では数多く「恋の力学」でも遊んできた。ただ、そこでは「惹かれ合う恋心の大きさ」だけに注目して、そのカップルの中での役割などは考えたことがなかった。そこで、今回は「やおい」のカップルの「役割・順序」に注目し、その「役割・順序」を評価する演算子を行列・ベクトルの掛け算になぞらえながら考えてみることで、これまでと同じく色々な「恋の形」を眺めてみたいと思う。
まずは、色々な人物(実際の人物であったり、小説などの登場人物であったり)のタイプを二次元空間に配置しよう。「この人は結構攻め役が合いそう」とか「この人は絶対受け役が合うのだー」という適性を
- 攻めベクトル
- 受けベクトル
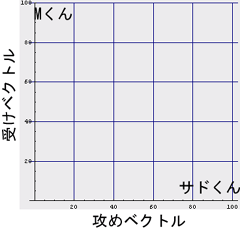 |
そして、カップリング適性では「A×B、B×Aが全然違う」ということから、外積(ベクトル積)をそのまま流用して、適当な評価関数を作ってみるのが自然だろう。まず、
カップリング適性ベクトル = (攻め度(s)、受け度(m))と表記して、例えばAさんのカップリング適性ベクトルを(As, Am)と表すことにしてみよう。すると、Aさんが「攻め」でBさんが「受け」のカップリング適性は、この二人の適性ベクトルのベクトル積として表すことができる。つまり、
A×Bのカップリング適性 = ( As * Bm - Am * Bs )となるわけである。式を眺めれば判るように、Aさんの攻め度が高くて、Bさんの受け度が高ければ、この評価関数は高い値を返す。つまり、「A×Bの順序は正しいのだー」という評価を返す。つまり、「A×B」はなかなか良いカップルだー、と教えてくれる。また、もしAさんの受け度が高くて、Bさんの攻め度が高ければ、低い値を返す。つまり、「A×Bの順序は絶対間違ってるのだー」と評価してくれるのである。なんともありがたいことに(いや別にありがたくはないか…)、この「やおいのカップリング評価演算子」が「福田X小泉」と「小泉X福田」のどちらが自然なのかを教えてくれるのだ。試しに、上のサドくんとMくんであれば、「サドくん×Mくん」= (100,0)×(0,100) = 100*100 - 0*0 = 10000でとっても「良い感じ」でああるが、「Mくん×サドくん」= (0,100)×(100,0) = 0*0 - 100*100 = -10000で「このカップリングは絶対順序が違うー」と判るわけである。
= Aさんの攻め度 * Bさんの受け度
- Aさんの受け度 * Bさんの攻め度
とりあえず、今回はこの評価演算子を作成するところまでで終えたいと思うが、いずれこの「やおいの評価演算子」を武器にして、いつか(?)「やおいの世界= やおい界」に限らず、色んな数多くの恋の関係を目に見えるようにしてみたいと思う。そして、これまで数多く考えてきた「恋の〜シリーズ」を充実させていきたいと思うのである。
ところで、今回のカップリング適性評価演算子は基本的に外積そのものである。つまり、この演算が返す値は「二人のベクトルでできる平行四辺形の面積」に等しい。つまりは、「二人のベクトルでどれだけ色んな違うことがきでるか」を示す尺度である。そして、その値は二人のベクトルが直交する時、すなわち二人のベクトルが重ならず独立である時に最大値となる。つまりは、「二人のベクトルが違えば違うほど大きく」なる。例えば、先の「サドくん×Mくん」であれば二人のS,M趣向が完全に正反対であったからとてもお似合いのカップルになったのである。
これをいわゆる恋の話で考えてみると、とっても独立な二人、趣味が重ならない二人がお似合いだということになる。なるほど、そんなカップルも世の中にはたくさんいることだろう。そんな人達を「外積タイプのカップル」と呼ぶことができると思う。
一方、趣味が重ならないカップルだけでなくて、世の中にはそれとは正反対の「趣味が重なる良いカップル」も数多くいる。それは「内積タイプのカップル」である。内積はA,Bベクトル間の正射影に比例する量であって、つまりは「二人の重なるベクトルの大きさ」である。それは例えば、相手の中に自分を重ね合わせるような「二人の重なる部分が二人を結びつけるようなカップル」なのである。
「理系と文系」・「男と女」が対極的なものでも、相反するものでもないのと同じく、「外積カップルと内積カップル」も別に二つに分けられるようなものではないだろう。「外積タイプの恋」も「内積タイプの恋」が混じり合って、それぞれに良いところもあれば、危ういところもあって、などと想像してみるのも面白いに違いない。そして、さらにはもしかしたらベクトル空間で萌えることができるようになったりするかもしれない。
そういえば、ふと考えてみると以前「恋の形を見た人は」で最後に引用した本橋馨子の「兼次おじ様シリーズ」は男性同士の恋の話だった。つまりは「やおい」の話だった。そこで、もう一度そのセリフを最後に飾って眺めてみようと思うのである。
「愛はどんな形をしているか知っているか?」「見た事ないからわかりません。」「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...
もし愛に優劣を決めるものがあればなんだろう?... 異性愛か、同性愛か、そんなものじゃない …たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」