2000-08-07[n年前へ]
■高いか、安いか、この価格 
愛はお金で買えるのでしょうか?
私がよく使う日本国内向け情報検索サイトはinfoseekである。何かを探すときには、居酒屋の生ビールではないが、何はともあれinfoseekである。何故かは上手く説明できないが、他の検索サイトに比べて私にとって感覚的に「合う」のである。
ところで、こういった検索サイトはバナー広告などの広告収入で運営されている。しかし、私は「そんなバナー広告って、高いお金を出すほど効果があるのかなぁ?」とかねがね疑問に思っている。といっても、広告シロートの感覚なのできっとそれは間違っているのだろう。
そんな広告シロートの私でも、「あぁ、これは便利だなぁ。これはきっと効果があるよなぁ。」と思うバナー広告がある。それは、「検索のキーワードに応じて表示されるバナー広告」である。
例えばinfoseekで「センサ」というキーワードで検索をかけるとこんな結果表示の画面になる。
 |
色々な「センサ」に関する情報を知りたいと思って、「センサ」に関するサイトをinfoseekで調べると、
センシング・計測技術の総合サイト = キーエンスというバナーがデッカク表示されるのである。なんとも、これは便利である。普通のバナー広告は邪魔なだぁと思うことも多いが、こんなバナー広告は全然邪魔だとは思わない。むしろ、便利だなぁと私は素直に思うのである。
私の気持ちに関わらず勝手に無条件で表示されるバナー広告は、私にとって単なるノイズにすぎない。「このバナー広告がなければ、もっと素早く情報が表示されるのになぁ」などと思い出すと、腹が立ってくるほどである。しかし、私の探している情報に関するバナー広告を表示してくれるとなると、それが180度変わるのである。それは単なるノイズではなくて価値あるシグナルに変わってしまうのだ。邪魔な存在から、とってもありがたい存在に変わるのである。
これは他の色々なキーワードでもそうで、例えばプリンターやコピー機の「トナー」に関する情報を探してみると、こんなバナー広告が表示される。「トナー」を探している人には
ウチでは安いトナーを売ってますよ!という広告を教えてくれるのである。なんともありがたいことである。これは決して邪魔ではない。むしろ、適切なアドバイスである(いや、もちろんここのトナーが本当に安いのかどうかは私は知らない)。
 |
この「センサ」、「トナー」といった例はinfoseekの場合だが、これは別にinfoseekに限るものではない。他の検索サイトでもこんなバナー広告は同様に表示される。例えば、
- excite ( http://www.excite.co.jp/)
- LYCOS ( http://www.lycos.co.jp/ )
- infoseek ( http://www.infoseek.co.jp/)
- goo ( http://www.goo.ne.jp )
 |  |
 |  |
どこの検索サイトでも「デジカメに関する情報を探している人」には「デジカメの広告」を表示してくれるのである。いやはや便利な時代になったものである(ちょっと年寄り風)。
ところで、こんな検索をかけている内に、こうした広告を出すのに「いくら位お金がかかるのか」と疑問に思い
を見てみると、これが実は結構安い。- Search Word/サーチワード 検索する言葉に合わせて出現する、待ち伏せ広告 (サイズ:60×468)
- 4週間2,500PV以上のワード 4週間で¥12×PV
- 上記外のワード 4週間で¥30,000 (固定)
- Top Page Banner/トップページバナー
私にとっては「邪魔な存在なだけのバナー広告」が一週間で¥2,000,000であるのに、「ありがたい存在のバナー広告」が4週間で¥30,000なのである。もう、こんなに安くて良いのかしら、という位である。こんなに安いと個人で広告を出してみても良いと思うくらいである。私も小遣いがもう少しあれば、試しに広告を出してみるところだ。「できる?」で検索をかけると、自動的に「HIRAX.NET」のバナー広告を表示したい程である。それは四週間で3万円なら安いモノだ。
それどころか、このバナー広告を使ったシュールなプロポーズなんてのもオツなものだと思う。例えば、こんな感じだ。
ホラ、キミinfoseekでキミの「運命の人」を検索してごらん。なんて具合である。しかし、そんなことはもう実はされているかもしれない。
アラ、アナタのバナー広告が出てるわ! 何てこと!
ところで、このinfoseekの広告についての情報を読んでいると、infoseekにアクセスするユーザーに関する
なんて面白い情報がある。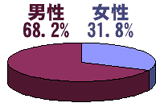 | 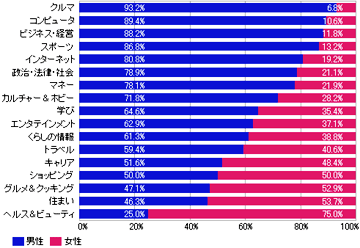 |
これを見ると、infoseekにアクセスするユーザーは男性がほぼ70%で、女性がほぼ32%であるから、これを標準の割合と考えて、チャンネル別男女構成比で「男の方が割合が高いジャンルと、女の方が割合が高いジャンル」を示すと次の図のようになる。
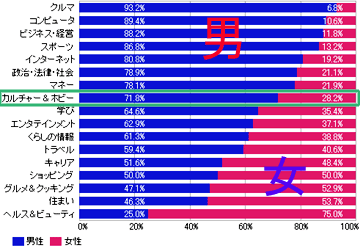 |
「カルチャー&ホビー」が男女半々のジャンルで、それを境にして「男の興味ある世界」と「女の興味ある世界」が分かれているのが判ると思う。「学び」に関しては女性の方が興味を持っていることが判るし、「インターネット」に関しては男性の方が興味を持っていることも判る。比較的、男性が「コンピュータ・ビジネス・経営・政治・法律・社会・マネー...」なんて無機的なものに興味を持っているのに対して、女性は「グルメ&クッキング・ショッピング・キャリア・トラベル・くらしの情報...」なんて血の通ったものに興味を持っている。うーん、面白い。男性の比率が一番多い(いや、女性の比率が少ないと言うべきか)のは「クルマ」で、女性は「ヘルス&ビューティー」だというのも何かとても面白く、笑ってしまう。
これを見ると、「住まい」なんかもうほとんど女性の支配する世界であることなども判るだろう。なるほど、「男の隠れ家」なんて雑誌が売れるわけだ。ここまで「住まい」が女性の世界であれば、それも当然だろう。
さて、話を検索キーワードに関するバナー広告に話を戻そう。試しにinfoseekで「結婚」で検索をかけるとこんな結婚情報サイトの広告が表示される。ありがたくて、涙が出そうになるくらいである。
 |
そこで、調子にのって私はexciteで「愛」で検索をかけてみた。
 |
もちろん、これは単なる偶然だろう。「愛」を探しているのに、消費者金融のバナー広告が表示されるわけはない。「愛」を探しているのに、「お金」の広告が出るわけがない。「愛がお金で買える」わけがない。単なる偶然とはわかっているけど、何ともイヤな偶然である。もちろん、単なる偶然の筈だ。
神様、愛はお金で買えるのでしょうか?
2001-03-04[n年前へ]
■柿ピーのシーソー・ゲーム 
柿とピーナツの供給バランスを考える
結婚しようとするカップルが少しばかり気にした方がよいのが、「柿ピーの好み」である。知らない人がいるとは思えないが、念のために書いておこう。柿ピーと言えば、柿ピー= 柿の種 + ピーナッツであって、亀田製菓の大ヒット商品である。そして、何と言ってもビールの安上がりのおつまみだ。
 |
この「安上がりで手軽なおつまみ」というところが、結婚しようとするカップルにはとても重要である。何故なら、結婚する前のカップルであれば洒落た店で飲むことも多いかもしれないが、結婚後はなかなかそうはいかない。いつの間にか手に持ったワイングラスは缶ビール(しかも発泡酒)に変〜身し、「テーブルの上の豪華な食事」はちゃぶ台の上の亀田製菓の柿ピーにバケラッタしているのである。
そうなると、かつては「このソースとても美味しいよね。うふっ。」なんて言っていた二人も変わらざるをえない。そりゃそうだ。柿ピーを目の前にして、気取ってみてもしょうがないわけだ。そんな時、こんな会話に走りがちである。
「柿の種ばっか、食べないでよ!」そう、柿ピーがなまじ「柿の種 + ピーナッツ」なので、片方がどんどん減っていったりすると、これがもう大変。かつては、ワインを片手に愛を語らっていた二人も、今やビール(しかも実は発泡酒)を片手に食い物の奪い合いをすることになるのである。
「オマエこそ、ピーナッツどんどん食えよ!」
これが、カップルの二人がとても似たもの同士で、「私達二人とも柿の種がスゴ〜ク好きだから、ピーナッツなんかいらないの。だから、- 柿の種だけが100%入った柿の種 - を買うの!」なんて感じなら、もちろんノープロブレムだろうし、あるいは、「ぼくらは、ピーナッツだけを買うのさ!」という感じのカップルでも同様だろう。
 |
あるいは、もう「ぼくは柿の種が好きだけど、きみはピーナッツが好き。二人は違っているから良い組み合わせなのさ。柿の種はぼくがどんどん食べるから、君はピーナッツをお食べ」なんてカップルでもいいだろう。こちらも、「ひとまずは」ノープロブレムである。つまりは、全く同じが正反対のカップルであれば、大抵の場合ほとんど問題はないのである。
しかし、「柿ピーは柿の種とピーナッツが適当な割合で入っているから良いのさ」なんていうグルメ気取りのカップルがいたりすると、大変である。
「アンタの食べる割合、少しおかしくない?」となるのは必至である。この数分後には、巨人の星の一徹父ちゃんのごとく、ちゃぶ台はひっくり返されているのに違いないのである。柿ピーの割合恐るべしだ。
「何言ってんだよ!オマエの方が柿ピー食べ過ぎだってんだよ!」
「そんなことないわよ!」
そして、しかもこれが理系カップルともなれば、もう最低だ。
「柿とピーの割合は7:3で食べなさいよ!」という具合になるに決まっているのだ。このままいくと、柿ピーを前にして離婚談義にもなりかねない。なんともオソロシイ話である。(* ピー柿は7:3でピーナツの方が多い。そんなのが実在することが私にとっては驚きである。)
「違うだろ、6:4が適正値に決まってるだろ!」
「そんなにピーナッツを食べたいなら、柿ピーじゃなくてピー柿*にしなさいよ!」
「別にピーナッツが過半数を超えるほどがイイって言ってんじゃねぇ〜!」
「何よ、もっと定量的に話しなさいよ!」
そういうわけで、「柿ピーの好み」「柿ピーの割合」「柿ピーの消費の割合」なんていうものは、結構結婚しようとするカップルには重要なのである。結婚しようとするカップルはぜひとも心して聞いておいてもらいたい。とはいえ、モテモテ度テストで
「女にモテない、というより、女に興味がないオマエ。今、一番気になることがドリキャスの値下げだったりなんかしない? まーそれも人生だけど、モテたほうがおいしいことは多いぜ? もうちょい女に関心持てよ。」と判定された私が言っても説得力がないか。
ところで、そもそも柿ピーの割合はどのくらいが普通なのだろうか?WEBで検索してみると、柿ピー10に対して
- 柿の種 : 7〜6
- ピーナッツ : 3〜4
そこで、試しに私も手元にあった小袋入り亀田の柿ピーの中身を調べてみた。調べたのは「小袋入り亀田の柿ピー」である。
 |
この一袋の中身を開けてみると大体こんな感じである。
 |
もちろん、単に数えても良いわけではあるが、「クダラナイことに、無意味なほどに大ゲサな道具を使うのがこのサイトのポリシー」でもあったりするので、まずは画像処理ソフトを使って柿の種とピーナッツの個数をカウントしてみた。使ったソフトはUTHSCSAImageTool である。PCベースでフリーでお手軽で粒子カウントとなるとこのソフトになるだろう。もちろんNIH-imageベースのScionImagePCという選択肢もないわけではないが、こと粒子カウントになるとはるかにImageToolの方が使いやすい。マクロの取っつきやすさ(機能は較べものにならないほどおちるが)もNIH-image系よりも上である。
さて、まずは上の画面内で柿の種を粒子カウントしてみたのが次の画面だ。この画面では見つかった柿の種は赤い縁取りがされ、個数がマーキングされていることがわかると思う。ちなみに、この画面内では93個の柿の種が見つかった。しつこいようだが、「数えた方が早いだろっ!」というツッコミはこの「できるかな?」では厳禁である。
 |
同じようにして、ピーナッツをカウントしてみたのが次の画面である。この画面では、ピーナッツは23個見つかった。
 |
すると、個数ベースでピーナッツが23/(93+23) = 20%で、残りが柿の種で80%ということになる。柿ピーの割合は大体8:2であったことになる。確か、WEBの亀田製菓に関する情報では
「柿ピー」のブレンドは、柿の種6に対してピーナッツ4が基本と書いてあったような気がするので、今回の8:2というデータは測定誤差、とその他の何らかの誤差が重なったものだろう。いや、そんな誤差はどうでも良いか。
ところで、大きな袋に入った柿ピーを食べながらよく考えることがある。私は柿の種が大好きなので、柿の種ばっかり選んで食べていくと、袋の口近くの上の方にはピーナッツばかりが残り、明らかに袋の場所ごとに柿の種とピーナッツの割合が異なってしまっていることがよくある。この柿の種とピーナッツの割合の時間的・空間的変化は一体どうなっているものだろうか?そこで、今回その「ピーナッツの柿ピーに占める割合の時間・空間的変化」について、少し考えてみることにした。
まずは簡単に判るように、袋の中から均等に柿の種とピーナッツを「柿ピーの割合を適当な割合で」食べていった場合、「ピーナッツの柿ピーに占める割合」は次の図のようになる。この図は横軸が時間で、縦軸がピーナッツの柿ピーに占める割合である。
緑 : 柿ピーを8:3の割合で食べた場合  |
今回の場合柿ピーは8:2で入っているので、青の場合のように柿ピーを8:2の割合で食べていくと、時間にして10分後に柿ピーがなくなるまで、ピーナッツの柿ピーに占める割合は20%をキープしたままである。しかし、(少しばかりピーナッツが好きな人が)柿ピーを8:3の割合で食べてしまうと、つまりピーナッツを過剰に食べてしまうと、どんどんピーナッツの割合は減ってしまい、ついに8分経過後にはピーナッツが袋の中から無くなってしまうのである。つまり、あとの2分は悲しみと共に柿の種を食べ続けなければならないのである(私は柿の種が好きなので悲しくもなんともないが)。
じゃぁ、袋の中の空間的分布も考えてみたらどうなるか、というのを次に計算してみた。まずは、袋を大きく二つに分けて、袋の入り口で適当な割合で柿ピーを食べた後、袋の奥から袋の入り口の方へ柿ピーを持ってくる。また、その際に適度に柿ピーをかき混ぜる。そして、柿ピーがなくなるまで柿ピーの割合の変化を調べてみるのである。ちなみに、IE4以降+Excel2000以降?の人であれば、ここをクリックすれば、その計算シートで遊ぶことができると思う。
例えば、「柿ピーを8:2の割合で食べた場合」と「柿ピーを8:5の割合で食べた場合」のピーナッツの柿ピーに占める割合の時間・空間的変化を調べてみたのが、次に示す結果である。ちなみに、このいずれも横軸は時間である。また、時間軸にして30前後の時点で柿ピーは完全になくなっている。
 ちょっと計算上の誤差が大きいが、それはちょっと無視してもらいたい。 |
さて、左の「柿ピーを8:2の割合で食べた場合」、つまり本来の柿ピー比と同じ割合で食べていった場合には、入り口近くでも奥の方でも柿ピーの比率は変わらない。そして、入り口の方から柿ピーを取った分を、奥の方から補給しているので、奥の方では時間軸20の時点で空になってしまっている。左の図でピーナツの割合がゼロになっているように見えるのは、実は単に柿ピーがなくなっただけなのである。そして、入り口近くの柿ピーが時間軸30の時点で空になっているまで、柿ピーの比率は変わることはない。当たり前だ。
では、「柿ピーを8:5の割合で食べた場合」はどうだろうか?つまり、本来の割合よりもピーナッツを多く食べがちな人の場合だ。そんな場合の右を見てみると、奥の方は単に入り口近くに柿ピーを補給しているだけなので、柿ピーの割合は変わらないままだ。しかし、入り口近くではあっという間にピーナッツの割合が減ってしまっている。ほとんどなくなっている、といっても良いくらいの状態である。つまり、ピーナッツ大好き人間にとっては、手の届く袋の入り口近くには全然ピーナッツがないという、拷問状態なのである。周りに女子校や共学の学校はあるけど、自分の通う学校が男子校だったみたいなキツイ状態である。ちなみに、私は高校時代に私服の共学の学校に通った結果、制服の女子高生に強い強い憧れを抱くに至ったことを否定できなかったりするのである。
話を戻して、それでは「袋を適当にかき混ぜながら」、「柿ピーを8:5の割合で食べた場合」はどうなるだろうか?というのが次の結果である。こうすると、奥の方のピーナッツもどんどん消費されているのがわかる。入り口近くも奥の方も、同じようにどんどんピーナッツの割合がどんどん減ってしまい、時間軸15の時点で完全になくなってしまっている。あとは柿の種がなくなる時間軸30の時点まではもう柿の種と向かい合うだけの人生なのである。ツラすぎる(ピーナッツ好きの人にとっては)。私の知人のオッパイ星人が結婚後に妻から、
*一部、不適当な発言がありましたことをお詫びします。
 |
つまりは、ピーナッツが食べたいからといって、あまり柿ピーの袋をかき混ぜるのは良くないということなのである。もちろん、短期的にはピーナッツがたくさん食べることができて良いわけであるが、長期的に見ればその後の長い「柿の種人生」が待っているのである。それが端的にわかるのが、次の「ピーナッツをどれだけ食べているか」を示す結果である。
この結果の中で、上の方に示した「柿ピーの袋をかき混ぜない場合」では、結構最後までピーナッツを細々と食べていけることがわかるだろう。柿ピーがなくなるのが時間軸で30前後の時点であるが、その少し前23位の時点までピーナッツを食べていけるのである。それに対して、ピーナッツを早く食べたいばかりに、柿ピーの袋をかき混ぜまくりの下の「柿ピーの袋をかき混ぜた場合」には、時間軸で13前後の時点でもうピーナッツがなくなってしまっている。もう、コイツには「柿の種人生」しか残されていないのである。
| 柿ピーの袋をかき混ぜない場合
結構最後までピーナッツを細々と食べていける |
| 柿ピーの袋をかき混ぜた場合
なんとも、太く短くのピーナッツの食べ方である… |
とはいえ、柿ピーの袋をかき混ぜながら太く短くピーナッツを食べるか、それをじっとガマンの子で細々と最後までピーナッツを食べるか、どっちが良いかは難しいところだ。ちなみに、私はかき混ぜまくりで柿の種を食いまくり、残ったピーナッツは人にプレゼントするというとても良い性格である。だったら、100%柿の種を買えって感じであるが、売店には置いてないことも多いから、しょうがないのである。
というわけで、今回はビール(やっぱりあくまで発泡酒)を左手にそして柿ピーを右手でつまみながら、酔っぱらった頭で(いつものことだが)、ツマラナイことを考えてみた。モノが本当の柿の種であればオチて芽が出るのが普通なのだけれど、今回の柿ピーの話はオチがあるわけでも芽が出るわけでもない。酔っぱらいのタワゴトだから意味なんか全然ないのである。と、日記には書いておこう(意味不明)。
2001-07-14[n年前へ]
■今日のE-Charger 4100の暗黒面 
HP 4100は新しく面白い特徴がある。それらは、消費者を喜ばせるが、リフィル業者を悩ませるものだ。そんな機能のひとつがカートリッジのをモニターしサプライ・ステータス・ページに印刷できる情報を本体に転送する機能である。
このページには、車のダッシュボードにあるメーター類と同じように、トナーや他の消耗品の量が印刷してある。プリンターに純正のカートリッジを使う限りは、その便利な機能はユーザーがこれまでどの程度印刷したかとか、どの程度のジョブを終えたかなどを正確に知ることができる。
しかし、である。再生カートリッジを使用している場合には、この機能はその暗黒面を見せるのだ。 Summit LaserでMike Josiahとテクニカル・チームが調べたサンプルによれば、サプライ・ステータス・ページには「注意 -- Hewlett Packardのものでないトナー・カートリッジが検出されました。このHewlett Packardのものでないトナー・カートリッジを使用した場合のサービスや修理はプリンター保証の範囲外です」と印刷された。
ここ数週間はこの「保証外」に対する苦情が届き、修理業者やOEMディーラーは顧客に「それは単にHPのカートリッジを使わなかった場合だけの話です」と説明している。(詳細はRecahrgerのWEB内記事参照)
この手の「海賊」対策はなんだかねぇ。と、個人的には思うが。
2001-12-24[n年前へ]
■私と二度めに出会う「水」 
クリスマスの小さな遺品
先日、こんなメールを頂いた。
私の娘は小学三年生。図書館から借りてきた「水の一生」といった、子供向け科学本(蛇口から出た水は下水を通って…<途中大幅に省略>…再度雨になって…というヤツです)を読んでおりました。そこで彼女はいくつかの疑問を口にしました。可愛い娘さんとお父さんの楽しそうな会話が伝わってくるメールである。「一度下水に流した水は、どのくらい経ったらまた私のところへ戻ってくるの?」さて、どう思われますか?
私 「必ずしもすべての水が海まで行くわけではなくて、下水処理場で蒸発して、川の取水口あたりで雨になる分子もあるはずだから、そうだなあ、一番早くて3日くらいかなあ。 勿論もっと長い場合もあるし、一度流したらキミが生きている間にはここには戻ってこない分子もあると思うよ」
「コップ一杯の水の中で、私と2度目に出会う水はどれくらいあるの?」私 「う〜ん… どれくらいなんだろう?」
ところで、この後半の疑問「コップ一杯の水の中で、私と2度目に出会う水はどれくらいあるの?」というのはたまに見かける話である。何かの小説で、「このコップの話が主人公が科学を志したきっかけになっている」という小道具に使われている例も読んだことがあるような気がする。
たまに見かける話ではあるのだけれど、同じ本を読んでも人それぞれ抱く感想は違うし、私なりにも考えてみたい気もしたので、今回はこの「コップ一杯の水の中で、私と2度目に出会う水はどれくらいあるの?」を考えてみることにした。
人が一日に「出会う」水はどの位の量だろうか?成人男子が安静にした状態で、一日当たり大体2.5リットルの水を消費するという。すると、小さい子供の場合でも、少なくとも一日2リットルくらいは水を消費する、つまり水と「出会って」そして「分かれる」ことになる。2リットルの水というと、2000gだから、これを水の1molあたりの重さ18g /molで割って、さらにアボガドロ数(1mol当たりの分子数)をかけてやると、(2l = 2000g ) / 18g x 6.022x1023個 = 6.7 x 1025個となり、私たちが一日に出会う水分子の数の個数がわかる。
この「とある一日に私たちが出会った水」が川へ流れて、海へ流れて、地球上にまんべんなく拡がったとしよう。地球上の限りなくある水の中に含まれる「とある一日に私たちが出会った水分子」の割合は、いったいどのくらいの程度になるのだろうか?
地球上の水は大体14億km3くらいだという。そのほとんどは96.5%は海水で、残りが陸地のさまざまな場所(そしてわずかに空気中)に存在している。この地球上にある水の重さを計算すると、14億km3= 1350000000km3 = 1.4 x 109 x 1012 kg= 1.4 x 1024 g ということになって、これを水の1molあたりの重さ18g /molで割ってやると、地球上に存在する水分子の総量は 1.4 x 1024/ 18 = 7.8 x 1022mol ということになる。mol数から水分子の量に直すために、アボガドロ数6.022x1023個/molをかけてやると、地球上の水分子の総量= 4.5 x 1046 個という数字が得られる。
すると、地球上の限りなくある水の中に含まれる「とある一日に私たちが出会った水分子」の割合は
「とある一日に私たちが出会った水分子」 / 地球上の水分子の総量 = 6.7x 1025個 / 4.5 x 1046 個 = 1.5 x 10-21= 0.00000000000000000015%というとても小さい割合になる。この割合は、新たに水分子と出会った時に、その水分子が「とある一日に私たちが出会った水」である確率と言い換えても良いだろう。とにかく、私たちの普段の生活の感覚からすれば、限りなく小さく思えてしまう。しかし、その再会の確率はとても小さく思えてしまうのだけれど、決して私たちは「とある一日に私たちが出会った水分子二度と水と再会しない」わけでは無いのである。
例えば、180mlのコップ一杯の水の中には( 180ml = 180g ) / 18g x 6.022x1023個= 6.0 x 1024個の水分子が含まれている。ということは、このコップ一杯に含まれる水分子の中にいる、かつて「とある一日に私たちが出会った水分子」の数を計算してみると、
コップ一杯に含まれる水分子の数 x 「とある一日に私たちが出会った水」である確率= 6.0 x 1024個 x 1.5 x 10-21 = 9000個ということになる。コップ一杯の水の中にはかつて「とある一日に私たちが出会った水」が一万個近くも存在していることになる。
しかも、この計算は「とある一日に私たちが出会った水分子」だけで計算していて、決して「これまでに私たちが出会った水分子」で計算しているわけではないのだから、「コップ一杯の水の中で、私と2度目に出会う水」はもっと多いことになる。もちろん、実際には私たちが消費した水が理想的に拡散したりはしないだろうから、こんな風に上手くはいかないだろうけれども。
とりあえず、「コップ一杯の水の中で、私と2度目に出会う水はどれくらいあるの?」という疑問を口にした小学校三年生の娘さんには、「ずっと昔のある日に出会った水がコップ一杯の中には一万個近くもあるかもね」と答えておくのが良いかもしれない。計算の中身、アボガドロ数なんて言っても、小学校三年生では「あぼがど?あぼがろど…?」と頭がこんがらがるだけかもしれないけれど、とりあえず「おとーさんって、何でもわかるんだー」とちょっとくらいは尊敬されたりするかもしれない。
そういえば、先日東京で初雪が降った。「雪は天から送られた手紙」とは中谷宇吉郎の残した名言だけど、その雪を見ながらこんなことを考えた。
ある日誰かが亡くなり、荼毘に付される。すると、その人の体のほとんどの部分は火と共に空へ昇っていくことだろう。成人の体のおよそ60%は水分だから、体重60kgの人であれば、その60%の36000gもの水が空へ還ってゆくことになる。その空へ還っていった水分子が世界中に散らばっていった後に、いつかまたその水分子と出会うためにはどの程度の水があれば良いだろうか?どの程度の水があれば、この中には「かつてあの人と共に空に帰っていった水分子」が一個くらいはある、と言えるものだろうか?
これを先程と同じように計算してみると、ほんのちょっと「1 x 10-3g」ほどの水があれば、その中には「かつてあの人と共に空に帰っていった水分子」が一個くらいある、という結果になる。「1x 10-3g」ということは、大きさで言うと1mm3ほどになる。ちょうど雨粒一滴と同じ位の大きさだ。空から降ってくる雨一粒の中には「かつて亡くなった人と共に空に帰っていった水分子」が1個が漂っている、ということになる。
冬の雪の一片の大きさが雨の一粒と同じくらいであるかは判らないけれど、今日のように何時の間にか雨が雪に変わることもあるくらいだから、やっぱり雪も雨と同じような大きさなのだろう。だとすれば、空から降ってくる雪の一片の中には、「かつて亡くなった人と共に空に帰っていった水分子」が1個宝石のように入っていてもおかしくはない。「雪は天から送られた手紙」であるならば、その中にはその手紙を天から送ってくる「かつて亡くなった人」のまるで遺品が1個づつ封じ込められているのである。「雪は天からの遺品」と言っても良いかもしれない。
間もなく、クリスマス。そして、クリスマスには白い雪が付き物だ。空から舞い降りてくる白い雪の中には大切な1個の水分子「クリスマスの小さな遺品」が入っているのである。
2002-09-16[n年前へ]
■通勤用新聞 
新聞の紙の面積のうち、大体60%弱が広告だといいます。「大規模に印刷するような紙」の文化は広告費が支えている分がとても大きいわけで、広告のスペースなどを抜いてダイジェスト版にしてしまうとその分だけ「とても高く」しないとペイしない…。その値段でも消費者が満足するか…?
と、そんな話がされていたのが先月末に参加したセミナーの一日目でした、ハイ。(リンク)(リンク)

