1999-07-05[n年前へ]
■目に映る明るさって何ですか? 
君は天然色
前回、デジカメ画像をスクリーンセーバーにしたい-記念写真を飾ろう - (1999.06.30)
を作るために、いくつか調べ事をした(ホントはずっと昔に)。それについてまとめておきたい。
調べたことは、
- カラーから白黒への変換はどうする?
- セピアカラーって一体何だ。
- セピアカラーへの変換はどうやろう?
カラーから白黒への変換はどうする? どうしよう? これは結構難しい問題(結果的にやったことは簡単でも、プロセスとしてはすごく難しい)だ。そうそう白黒の世界を見たことのある人はいないだろう。特殊な状況下(たとえば、すごく暗い所とか)では色を感じないこともあるだろうが、普通の世界は天然色である。フルカラーの世界だ。そもそも明るさって一体何だ?(明快に答えられる方教えてください。) 例えば、下の図で明るい順番はどうなっているだろうか?自信を持って答えられるだろうか。
 |
とグチを言っていてもしょうがないから、決めてしまおう。うす暗い(1lx程度)部屋で景色を眺めてみよう。その時見える世界が、明るさの世界だ。そこには色など存在しない。確かめて欲しい。今回は、とにかくそれを「明るさ」の尺度としてしまおう。
(興味ある方は明るさを測ろう- 新技術の女神 -(1998.11.13)もご覧下さい)
次に明るい部屋へ移動する。そこでは、新たなものが加わる。それが「色」である。ということで、「明るさ」+「色」で世界を表現することにしよう。
いきなりではあるが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。
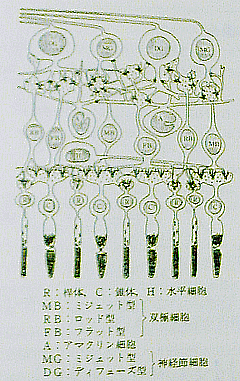 「視覚と画像」 大頭・行田 著 森北出版より |
それでは、明るい部屋で感じる色はどうなっているだろうか。色を感じる錐体の中には波長感度の異なる3種類の視物質がある。それぞれの波長感度を以下に示す。
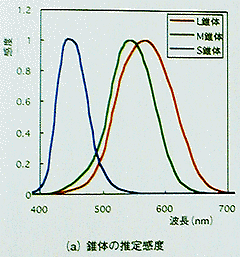 CQ出版 洪 博哲著 「お話・カラー画像処理」より |
次に、それらの3種類の視物質による錐体が組み合わさった時の波長比視感度を以下に示す。点線で示してあるほうは比較的暗い場所での波長比視感度なので、今回は無視して欲しい。
 「視覚と画像」 大頭・行田 著 森北出版より |
後は、このグラフを元に赤、緑、青の3点で重み付けしてやれば良いだろう。
というわけで、グレー化のために使っているのはこの式だ。
- Red: ptr[2]
- Green: ptr[1]
- Blue: ptr[0]、として
やっと、ここまで辿りついた。結局使うのはこんな簡単な式なんだ、っていうツッコミは無しにして欲しい。同じ式を使うのでも、私はそこまでのプロセスも重視したいのだ。
さて、こういった色を扱う話題であれば、脇色彩研究所のWEB(http://www.mmjp.or.jp/rwicp/ )中から
- 色に対する感じ方(眼とフィルム)( http://www.mmjp.or.jp/rwicp/data106.html )
- カラーフィルムの特性と色再現( http://www.mmjp.or.jp/rwicp/filmirosai.html )
- 明るさの見え方(明暗対比)( http://www.mmjp.or.jp/rwicp/data506.html )
- 色覚、眼の色に対する感じ方( http://www.mmjp.or.jp/rwicp/data509.html )
また、文中でも書いたが、「明るさとは***ということだ」と明快に答えられる方は私に是非教えて頂きたい。もし、素晴らしい答えが頂けたら、粗品(言葉通りの)を進呈しても良いと思っているくらいだ。
なお、以下のような答え方は遠慮致したい。
例1:
私 「液体と固体はどう区別するの」
A 「融点を境にして上と下」
私 「....」
例2:
私 「クジラは哺乳類、魚類どっち?」
A 「卵生まないから哺乳類」
私 「...」
1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
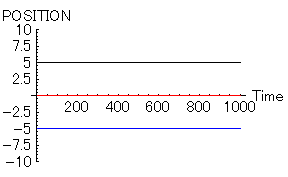 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
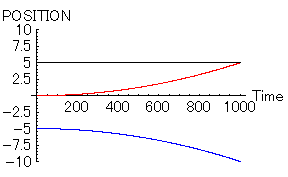 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
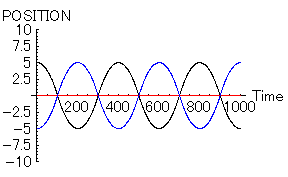 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
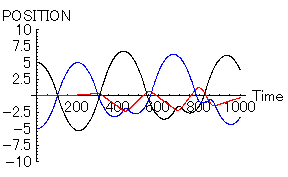 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)
2000-04-01[n年前へ]
■恋の力学 恋の相関分析編 
「明暗」の登場人物達の行方
「恋の力学」シリーズである。前書き編が登場したきりで、なかなか本編に入らない「恋の固体物理学」シリーズではない。今回は、
の続き、ということになる。以前、
の中で書いたように、恋の力学シリーズは夏目漱石の影響を多大に受けている。そして、同様に夏目漱石の影響を受けているシリーズがある。それは「文章構造可視化シリーズ」である。何しろ、「文章構造可視化シリーズ」は夏目漱石をきっかけとして、始まっているのである。また、シリーズの中の話を見ればわかるように、
- 夏目漱石は温泉がお好き?- 文章構造を可視化するソフトをつくる - (1999.07.14)
- 失楽園殺人事件の犯人を探せ- 文章構造可視化ソフトのバグを取れ - (1999.07.22)
- 「こころ」の中の「どうして?」 -漱石の中の謎とその終焉 - (1999.09.10)
- 「星の王子さま」の秘密- 水が意味するもの - (1999.11.15)
そのための準備として、まずは「文章構造可視化シリーズ」で作成した"wordfreq"をバージョンアップしてみた。その動作画面を以下に示す。
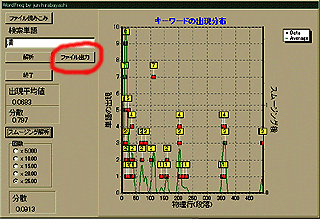 |
赤丸で示したボタンに「ファイル出力」と書いてあるのがわかると思う。つまり、文章中に「任意の単語」が出現した出現頻度を解析した結果をファイル出力する機能を持たせたのだ。1段落中に「任意の単語」が出現した数をテキスト形式で出力するようにしてある。このファイル出力結果を他のソフトに読み込めば、色々な解析ができるわけだ。いつものように、このソフトはここ
においておく。言うまでもないが、アルファ版の中のアルファ版だ。さて、今回用いるテキストは
でも登場した「明暗」である。そこで、「青空文庫」から「明暗」の電子テキストをダウンロードした。そして、バージョンアップした"wordfreq"で- 津田
- お延
- 清子
- 吉川
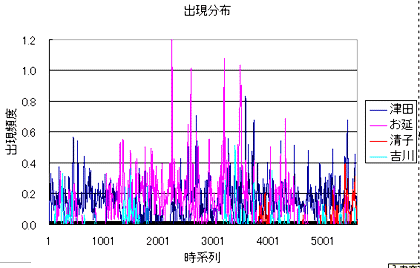 |
しかし、これだけでは、よくわからない。せいぜい「清子」が小説の後半(といっても、未完であるが)に登場しているなぁ、という位だろう。しかし、さらに解析を加えてみると、もう少し面白いことがわかる。
今回は、これらの登場人物間のお互いの関わりを調べたいのである。であるならば、これらの「登場人物」の出現分布の間の相関を調べてみると面白いだろう。互いの関係を示す「相関」を調べてみるのである。異なる「登場人物」が同じような出現をしているならば、それは無関係ではない。きっと、その登場人物の間には何らかの関係があるに違いないのだ。
そこで、「明暗」を時系列的に6つの部分に分けて、津田と他の登場人物の出現分布間の相関を調べてみたのが次のグラフである。
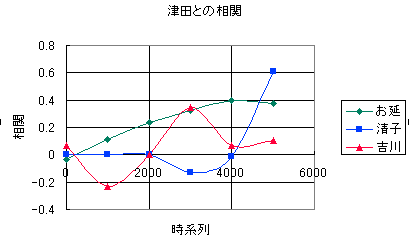 |
このグラフでは、横軸が時系列であり、縦軸が相関を示している。縦軸で上になればなるほど相関が高い、すなわち、「関係がある」のだ。「相関」は本人の場合で「1」である。だから、例えば最後の部分の清子の「0.6」という結果は関係がアリアリということを示しているわけだ。
また、「清子」と「吉川(ここでは夫人を意図している)」の相関が逆であることが面白いだろう。「吉川」が活躍(暗躍?)した後に、「清子」が登場するわけだ。
そして、この「明暗」が盛り上がっていくようすすら、見えてはこないだろうか?全く血の通っていないPCが解析した結果が、漱石の描こうとした「こころ」の動きを読みとっているような気が(少しは)しはしないだろうか?そして、このグラフの延長線上に、漱石の描くはずだった、「明暗」の結末はあるはずなのだ。
さて、このグラフを見ていると、
で計算した恋の多体(三体)問題の計算結果を思い出してしまう。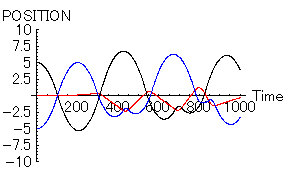 |
漱石は、きっと恋の三体問題を意識しながら「明暗」を書いたのである。だから、ある意味当然なのではあるが、科学と文学の一体化した世界が感じられ、とても面白い気分である。さて、この解析結果を元にして、まだまだ色々とやってみたのであるが、それは次回である。
2000-04-02[n年前へ]
■恋の力学 恋のグラフ配置編 
「明暗」の収束を見てみよう
前回、
で漱石の「明暗」における登場人物- 津田
- お延
- 清子
- 吉川
前回は、「津田」と他の登場人物の間の相関しか考えなかった。しかし、登場人物達の動きを考えていくならば、相互の相関を考えなければならないだろう。「続 明暗」の例を挙げるまでもなく、「明暗」の登場人物達がどこに収まっていくのか、「明暗」はどう収束していくのか、は非常に興味のあるところである。そこで、ラスト近辺の各登場人物間の相関を調べてみた。
津田 | お延 | 清子 | 吉川 | |
津田 | 1 | |||
お延 | 0.38 | 1 | ||
清子 | 0.61 | 0.42 | 1 | |
吉川 | 0.10 | 0.063 | 0.26 | 1 |
比較的大きな値の数値を青字で示した。有意であるかはともかく、この数値を見ると、話が「津田」、そして、「清子」を中心として動いていることが想像される(数値からだけでも)。
このような相関、言い換えれば関係を登場人物達が持っているときに、この後人物達の関係はどこに収まっていくのだろうか?この相関値を「互いの関係度」と考え、その値に比例して惹かれ合うと考えたときに、登場人物達はどう動いていくのだろうか?そういったことを調べたならば、そこに示される結果は書かれることのなかった「明暗」の収束する先が示されているかもしれない。
そこで、登場人物達を適当に配置して、登場人物間に働く力を考慮して、登場人物を動かした際に、結果として登場人物達がどこへ動いていくかを調べてみることにした。使うのは、もちろん"Sun"のJavaappletのプログラム例のグラフアプレットである。複数のものがあり、それぞれの関係が示された場合に、どのような配置になっていくかを調べる「グラフ配置問題」を解いてみるのである。今回の問題では、「恋のグラフ配置問題」を解くといっても良いだろう。
もう、いきなりであるが、登場人物
- 津田 = Tsuda
- お延 = Oen
- 清子 = Kiyoko
- 吉川 = Yoshikawa
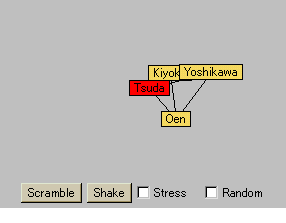 |
どうだろうか?「津田」を中心として、登場人物が蠢いているのがわかるだろう。適当に登場人物の位置をマウスで移動させてみると面白い。そして、互いの"Stress"を示してみると面白いと思う。
また、「明暗」の登場人物達の運命を、自分のマウスでコントロールしてみるとどんな感じだろう?それとも、どんな位置に登場人物を持っていっても、結局収まる位置は変わらなかったりするだろうか? だとしたら、それがやはり本来の登場人物の収まる位置かもしれない。
いつか、登場人物間全てを配置して、「明暗」における「人間関係のグラフ配置問題」でも考えてみたいものだ。「恋の力学シリーズ」は奥が深い、とつくづく思うのである。
2000-09-02[n年前へ]
■もうすぐ二歳の「できるかな?」 
初心に帰ってみましょうか?
「できるかな?」が始まったのは二年近く前の秋のことだった。
でも触れたが、当初(実は今も続いているが)は某社内の某サーバー内でこっそりと始めてみたのだった。それから二年あまりでずいぶんと色々な話が増えた。某社サーバー内でしかアップしていない- プリンタドライバーは仮免
- 続 電子写真プロセスを分数階微分で解いてみよう
- 続々 電子写真プロセスを分数階微分で解いてみよう
そして話が増えてきたせいか、自分自身でも「アレッ、あの話はどこにあったけ?」というように迷ってしまうことが多々ある。迷うどころか、最後まで見つからないこともしばしばあるのだ。そして、それは私でもない他の人であればましてやそうだろう。というわけで、
では簡単にそれまでの話の紹介をしたし、ではhirax.net内の全文検索機能を付けてみた。今回は、これまでの話題をもう一度自分で読み直して、その中から「自分のお気に入り」を調べてみたいと思う。そして、最近少し話題が変になってしまっている反省をして、もう一度初心に帰ってみようと思うのだ。
まずは、1998年の話題からいくと
というあたりが、良い感じだ。京都の風物詩である「鴨川カップル」達が人目を気にしながら寄り添う合う姿を考えてみたものだ。後の「恋の力学」シリーズなどはここらへんから始まっていた、といっても良いだろう。そしてこの頃の[Scraps]系の話題としては、がある。少し前に、この「さなえちゃん」を描いた漫画の作者からメールを頂いたのがとても私には印象深かった。そして、1999年の上半期から選んでみると、まずは
というところだろう。ハードディスクの情報を可視化することで情報圧縮・エントロピーを考えてみた一話である。そして、同じような「可視化シリーズ」の一つである- 感温液晶でNotePCの発熱分布を可視化する- 熱いところで感じてみたい St.Valentine 記念 - (1999.02.14)
- NotePCの発熱分布を比べてみたい- お熱いのがお好き SOME LIKE IT HOT - (1999.02.15)
そして、1999年の下半期はもう自分で言うのも何だが傑作揃いである。大体、書いているペースが自分でも驚くくらいのハイペースだ。月当たりの話の数を数えてみると、
- 7月 9話
- 8月 9話
- 9月 8話
- 10月 8話
- 11月 11話
- 12月 9話
この頃の「お薦めの話」はいっぱいある。例えば、
に始まった「文章可視化シリーズ」や、で始まった「ASCIIアートシリーズ」だろう。から始まる「江戸五色不動シリーズ」は江戸にロケまで行ったので、とても思い出深い話の一つである。しかも、妙な偶然のせいでまるで小説の中に迷い込んだような気持ちになったものだ。そして、WEBページを作る上では
などもどうしても外せない。そして、この後結構続くことになるという「恋の力学」シリーズもこの時期に始まっている。そして、この頃の一番人気が何と言ってもだろう。この「ミニスカート」系の話の流れは以降も続くことになるのが自分では意外でもあり、残念でもある。それはさておき、ナンセンス系ではなんてのも面白い話だと思う。そして、1999年の終わりはやはりこれが「お気に入り」の話である。また、[Scraps]系の話がこの時期にはやたらいっぱいあるのが面白いところだ。その内からいくつかピックアップするとこんな感じだろうか?- [Scraps]絵馬 - どこにもいないよ- (1999.07.09)
- 新宿駅は電気羊の夢を見るか- 意識とは何か - (1999.07.10)
- [Scraps]合掌 - キレイはキタナイ、キタナイはキレイ- (1999.08.01)
- [Scraps]いつかきっと -掌の中の答え - (99.11.03)
- 「文学論」と光学系 - 漱石の面白さ-(2000.02.27)
- 恋の力学 恋の相関分析編- 「明暗」の登場人物達の行方 - (2000.04.01)
- 恋の力学 恋のグラフ配置編- 「明暗」の収束を見てみよう - (2000.04.02)
- 恋する心を見てみたい - 恋のきっかけはどの出来事?- (2000.05.14)
- 恋の形を見た人は - 恋の相対性理論- (2000.05.17)
さて、今回は2000年上半期までの話の中から「私の好きな話」を振り返ってみた。とはいえ、私の好きな話=他の人の好きな話ではないようだし、他の話も適当に眺めて頂いたら良いかなぁ(私が)、と思うのだった。