1999-01-14[n年前へ]
■ボケたエアーブラシで細かな字がかけるか? 
画像復元を勉強してみたい その2
「宇宙人はどこにいる? - 画像復元を勉強してみたい その1-」ではボケた画像からオリジナルのシャープな画像を復元してみた。前回の話を例えて言うと、
- 太郎君が細かい字をエアーブラシで書いた。
- ボケボケのエアーブラシを使ったから、ボケボケの画になった。
- そのボケボケの画から、太郎君が何を画こうとしたか、考える。
ということであった。
今回、やってみたいのは以下のようなことである。
- 太郎君は太いエアーブラシで字を書きたい。
- しかも細かな字を書きたい。
- そんなことができるか?
直感的には、ボケボケのエアーブラシで細かい字など書けないように思う。その直感が正しいか調べてみたい。考え方は前回と同じく、
出力画像から、ボケ分布でデコンボリューション処理により、オリジナルの画像を計算する。
というやり方である。前回と違うのは出力画像がシャープな画像(先の例で言うと、細かな字)である、という所である。道具は今回もMathematicaを使う。
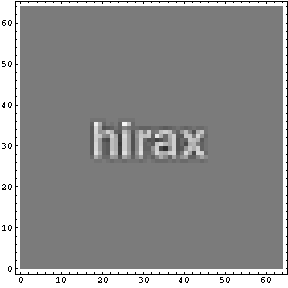
出力したい画像ファイルを読み込む。
<< Utilities`BinaryFiles`
StreamFile = OpenReadBinary["E:\jun\private\dekirukana\ufo\ufo.raw"]
ImageData = Table[ ReadBinary[ StreamFile , Byte] ,{x,64},{y,64}];
ListDensityPlot[ImageData,Mesh->False,PlotRange->{0,255}]
 |
この細かな字を太いボケボケなエアーブラシで字を書けるか考える。
まずは、エアーブラシのボケボケ度をつくる。
(*正規分布=ガウス分布によるぼけパラメータを作成する*)
δ=10;
μ=32;
ListPlot3D[NormalBoke,ColorFunction ->Hue,Mesh->False,PlotRange->All]
 |
ボケボケの太いエアーブラシである。
デコンボリューション用にガウス分布の場所をずらす。
NormalBoke = RotateRight[NormalBoke,32];
NormalBoke = Transpose[ RotateRight[Transpose[NormalBoke],32] ]; (*上へShift*)
ListPlot3D[NormalBoke,ColorFunction ->Hue,Mesh->False,PlotRange->All]
 |
出力画像をエアーブラシのボケボケ度でデコンボリューションする。そうすれば、太郎君がどのように画を画けば良いかがわかる。はたして答えはでるのだろうか?
計算してみると答えが出てしまう。
SharpImage = Re[InverseFourier[ Fourier[ImageData] / Fourier[NormalBoke]] ];
ListDensityPlot[SharpImage/4,Mesh->False,PlotRange->All]
 |
まず、本当にこれ(画像:4)にそってエアーブラシで画を画くと出力画像(画像:1)が再現できるか確認してみる。そこで画像:4と画像:3でコンボリューションしてやる。太郎君に実際にエアーブラシを使って画を画いてもらうわけである。
それでは、画いてみる。
ResImage = InverseFourier[Fourier[SharpImage] Fourier[NormalBoke]];
ListDensityPlot[Re[ResImage],Mesh->False,PlotRange->All]
 |
画像:1が再現できた。つまり、太いボケボケのエアーブラシで細かい字が書けてしまうわけである。直感的には納得しがたい結果である(私だけかもしれないが)。
これには実はタネがある。画像:4を鳥瞰図でみると判るが、画像4は正負の値が高周波で並んでいる。
ListPlot3D[SharpImage/4,ColorFunction ->Hue,Mesh->False,PlotRange->All]
 |
太郎君が使ったエアーブラシは太いボケボケのエアーブラシではあるが、吹き量に正負が両方ともあったのである。そのようなエアーブラシを使うと太郎君の腕(高テクニシャン)ならば細かな字が書けるわけだ。どんなパターンもかけるかはどうかまでは知らないが、少なくとも"hirax"という字は画ける。
前回のような光学系の例でも、これが何に対応しているかはすぐわかるが、一番分かりやすいのは電荷と電位の例だと思う。
電荷が周囲につくる電位分布はボケボケの分布である。ところが、金属などを適当に配置して、その金属に電位を印加してやると、鋭い電位分布をつくることができる。つまり、ボケボケの分布から鋭い電位分布を作成してやることができる。こちらなら直感的にもすぐ納得できるだろう。その際には、金属表面に電荷が鋭く集中するのも、よく知っている話だ。
実感用に電場計算を行った例を以下に示しておく。使った道具はCUPSの電場計算プログラムである。CUPSは教育用のプログラム集である。
一応、2次元膜の例で、金属を配置し、適当に電位を印加し、電位・電荷量計算を行ってみる。
 |
もちろん、金属内部では均一な電位である。それを条件に解いているのだから当たり前だが。
その時の電荷分布を下に示す。金属表面に鋭い電荷分布が生じているのがわかるだろう。
ここでは大雑把な金属の配置にしてしまったが、格子状の金属配置にして、互い違いに違う極性の電位を印加すれば(細かい字に相当する)、正負の極性の電荷分布が鋭く現れるのは当たり前の話だ。
 |
電位、電場、電荷量を一緒に示しておく。
 |
今回の話は、単なる計算上の話である。それに、何かどこかで仮定を間違っているような気もするんだよなぁ。信用度アルファ版だからまぁいいか...
1999-02-28[n年前へ]
■分数階微分に基づく画像特性を考えてみたい 
同じ年齢でも大違い
前回、分数階微分の謎 - 線形代数、分数階微分、シュレディンガー方程式の三題話- で分数階微分について調べた。例えば、0.7階微分といった、整数階でない微分である。今回はそれを使った応用を考えてみたい。
人間の視覚というものは明るいものは強く感じることができる。これは当たり前である。そして、それだけでなく、強さが変化している所にも(興味を)強く感じ取るようになっている。岡本安春氏の「Delphiでエンジョイプログラミング」によれば、そのような考えはLaming(1986)がdifferential coupling(差動結合)として発表しているらしい。
ということは、人間が画像を感じる特性というものは、画像強度と画像強度変化(画像強度の一階微分)の中間的なものであると言うことができるかもしれない。とすれば、分数階微分を導入すれば面白い表現ができるかもしれない。
今回は、そういう考えのもとに分数階微分を用いて人間の画像特性について考えてみたい。
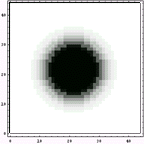
まずは、元画像を示す。元画像はガウス分布に基づいて作成されたものである。
 |  |
まずは、左の元画像を見て欲しい。どこに強い感じを受けるだろうか?白い部分はもちろんであるが、白と黒の境界部にも強い感じを受けるだろう。ギザギザになっているのはデータが少ないからなので、無視して欲しい。というわけで、人間の視覚画像特性は
- 画像強度
- 画像強度変化(画像強度の一階微分)
 元画像 |  |
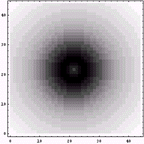
 1/2階微分画像 |  |
 15/20階微分画像 |  |
 1階微分画像 | 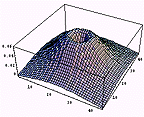 |
白地に黒画像バージョンも示しておく。紙の上の画像に慣れた人にはこちらの方が良いだろう。
 元画像 |
 1/2階微分画像 |
 15/20階微分画像 |
 1階微分画像 |
なお、今回の画像の作成は次のような手順で行っている。
- 1次元のガウス分布を作成する。
- 微分値が正であるような半分の領域を線対称に回転させ、2次元画像を作成する。
今回は
- 画像強度
- 画像強度変化(画像強度の一階微分)
- 電位
- 電界(電位の微分、といっても本来は電位が電界の積分か)
- 人口密度
- 人口密度変化(人口密度の微分)
さて、分数階微分を調べる中で、バナッハ空間についても調べた。調べ始めた時には、聞き覚えもなかったが、調べてみるとヒルベルト空間の導入で登場していた。きれいさっぱり忘れていたようである。
京大数学教室 徳永健一氏のWEB (http://www.kusm.kyoto-u.ac.jp/~kenichi/)
から辿れる「「年齢の本」数学者版」によれば
バナッハがバナッハ空間を提唱したのは30歳の時であるらしい。(http://www.kusm.kyoto-u.ac.jp/~kenichi/age/30.html)
うーん...
1999-03-25[n年前へ]
■電界計算をしてみたい[有限要素法編その1] 
有限と微小のパン
今回のサブタイトルは一目瞭然であるが、森博嗣のミステリのタイトルそのままである。
 |
何故、「電界計算をしてみたい-有限要素法編その1-」が「有限と微小のパン」に繋がるのか。もちろん、"有限要素法"と"有限と微小のパン"の「有限」をかけた駄洒落ではない。有限要素法を考えるとき、私は森博嗣に足を向けては寝ることができない。それが、なぜかは下の本を見ればわかる。
 |
これは、学生時代に有限要素法を勉強するために使った本である。「森 博嗣 著」と書いてあるのがわかるだろうか。いや、まさかこの本の作者がミステリを量産するとは想像もしなかった。ビックリである。講談社ノベルズと森北出版の両方から本を出している人は他にはいそうにない。
本題と関係のない話はここまでにしておく。今回はMathematicaで有限要素法を用いて静電界計算を行いたい。とりあえず、ソルバーとプリ・プロセッサまでつくる。その応用は続きの回で行いたい。Mathematicaで有限要素法を勉強するには、森北出版の依田 潔 著「Mathematicaによる電磁界シミュレーション入門」を参考にした。任意の電荷配置のPoisson方程式を解くようにしてある。
次回に詳しく計算モデルの説明を行うので、今回は計算モデルの詳細については記述しない。Notebook内に、モデルの詳細は記述してある。
このNotebookを使った計算、出力例を以下に示す。
| 平行平板電極の間に誘電体層があるモデル | 平板電極と三角柱電極の間に誘電体層があるモデル | 平板電極と円柱電極の間に誘電体層があるモデル |
 分割要素 |  分割要素 |  分割要素 |
 電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |
 半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |
Mathematica3.0のHTML出力は大変便利だが、漢字が化けるのが困りものだ。しかも、ちょっと似た漢字に化けてしまうからわかりにくい。今回のNotebook中で化けた漢字を以下に示す。
- 油界 <- 電界
- 堰素 <- 要素
- 誘油 <- 誘電
- 姦み込む <- 組み込む
- 表傭 <- 表面
- 壓さ <- 高さ
- 堆心 <- 重心
- 肖似 <- 近似
- 内占 <- 内部
- 傭積 <- 面積
- 回寂 <- 回転
- 進当 <- 適当
- 懷瞰 <- 鳥瞰
中国語みたいな化け方である。しかも、意味としても何か変な化け方である。いつか、この対処方法と理由を考えてみたい。それにしても、週末の遊び道具としてはMathematicaは素晴らしいと思う。
1999-06-10[n年前へ]
■コピー機と微分演算子 
電子写真プロセスを分数階微分で解いてみよう
前回、
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
の中で、電子写真プロセスは「画像のエッジ部分が黒くなり、そうでないソリッド部分は画像が飛びやすい... 画像のエッジ部分、すなわち、電位変化が大きく、電界強度の高い部分に対してトナーが現像されやすい... 」という文章がある。この脈絡は何か見覚えがないだろうか?そう、
分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
の中の、「人間が画像を感じる特性というものは、画像強度と画像強度変化(画像強度の一階微分)の中間的なものであると言うことができるかもしれない。」という文脈と似ている。また、「ゼロックス...」の回での(昔の)電子写真の特徴、
- エッジ強調される。
- 細かいところはボケてしまう。
参考までに、以前の話のときに用いた画像を示しておく。
まずは、
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
における(昔の)モノクロコピーを模したものである。
 |  |
分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
の際に解析した元画像と0.75階画像である。ただし、この解析は2次元解析ではなく、1次元における計算を回転させて、中心対称な画像を作成している。その理由は前回述べたので今回は述べない。
 |  |
それでは、解析を始める。まずは、Photoshop5による「(昔の)コピー機シミュレーション」である
 |  |
次が、分数階微分画像だ。今回もMathematicaを用いて計算している。検算が終了したら、Notebookも公開予定だ(実は検算が終了していないのだ...)。
 |  |
胸を張って「似ている」と断言するつもりはないが、少しは似ているのではないだろうか。別に似るまでがんばっても良いのだが、この分野の話はあまりやりすぎるわけにはいかないのである。ということで、強引ではあるが、今回の話の結論は「アナログコピーはオリジナルコピーの0.75階微分だ」というところで終わらせてもらう。
今回は、コピー機によるコピーを微分演算子と結びつけてみたわけだが、複数回のコピーに適用してみると面白いだろう。例えば、孫コピーは0.75+0.75階微分=1.5階微分であるとかだ。
また、同じ現像プロセスといっても色々あるわけであるから、各現像方式により微分演算子の階は異なるのが適当だろう。例えば、この機械は0.8階微分(つまりほとんどエッジ現像)であるが、こちらの機種は0.05階微分(極めて元画像に近い)で再現性に優れる、などという論議もできるかもしれない。
ところで、某所で今回の話と似て非なる話がCoffeeBreakとして公開されている。しかし、そちらは一般公開されていない。というわけで、今回は分数階微分の第3話ではなく、第4話ということになる。STARWARS風に言えば、Episode4だ。STAR WARSのようなSF映画もそうであるが、こういった話は生物(なまもの)である。ずっと置いておくと腐ってしまう。「腐ってこそ美味い食べ物もある」、という反論も聞こえてきそうだが、そういったものは少数の例外である。味オンチの料理人の作ったものではあるが、どうか賞味期間内に味わって頂きたい。
1999-09-01[n年前へ]
■画像に関する場の理論 
ポイントは画像形成の物理性だ!?
今回は、
夏目漱石は温泉がお好き? - 文章構造を可視化するソフトをつくる- (1999.07.14)
の回と同じく、「可視化情報シンポジウム'99」から話は始まる。まずは、「可視化情報シンポジウム'99」の中の
ウェーブレット変換法と微積分方程式によるカラー画像の圧縮および再現性について
という予稿の冒頭部分を抜き出してみる。「コンピュータグラフィックスを構成する画素データをスカラーポテンシャルあるいはベクトルポテンシャルの1成分とみなし、ベクトルの概念を導入することで古典物理学の集大成である場の理論が適用可能であることを提案している」というフレーズがある。
着目点は面白いし、この文章自体もファンタジーで私のツボに近い。しかしながら、肝心の内容が私の趣向とは少し違った。何しろ「以上により本研究では、古典物理学の場の理論で用いられるラプラシアン演算を用いることで、画像のエッジ抽出が行えることがわかった。」というようなフレーズが出てくるのである。うーん。
私と同様の印象を受けた人も他にいたようで(当然いると思うが)、「エッジ強調・抽出のために画像のラプラシアンをとるのはごく普通に行われていることだと思うのですが、何か新しい事項などあるのでしょうか?」という質問をしていた人もいた。
また、話の後半では、画像圧縮のために、ラプラシアンをかけたデータに積分方程式や有限要素法などを用いて解くことにより、画像圧縮復元をしようと試みていたが、これも精度、圧縮率、計算コストを考えるといま一つであると思う(私としては)。
画像とポテンシャルを結びつけて考えることは多い。例えば、「できるかな?」の中からでも抜き出してみると、
- 分数階微分に基づく画像特性を考えてみたい- 同じ年齢でも大違い - (1999.02.28)
- ゼロックス写真とセンチメンタルな写真 - コピー機による画像表現について考える- (99.06.06)
- コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
現実問題として、実世界において画像形成をを行うには物理学的な現象を介して行う以外にはありえない。「いや、そんなことはない。心理学的に、誰かがオレの脳みそに画像を飛ばしてくる。」というブラックなことを仰る方もいるだろうが、それはちょっと別にしておきたい。
「できるかな?」に登場している画像を形成装置には、
コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
で扱ったコピー機などの電子写真装置や、
宇宙人はどこにいる? - 画像復元を勉強してみたいその1-(1999.01.10)
で扱ったカメラ。望遠鏡などの光学系や、
ヒトは電磁波の振動方向を見ることができるか?- はい。ハイディンガーのブラシをご覧下さい - (1999.02.26)
で扱った液晶ディスプレイなどがある。そのいずれもが、純物理学的な現象を用いた画像形成の装置である。
例えば、プラズマディスプレイなどはプラズマアドレス部分に放電を生じさせて、電荷を液晶背面に付着させて、その電荷により発生する電界によって液晶の配向方向を変化させて、透過率を変化させることにより、画像を形成するのである。
 |
また、逆問題のようであるが電界・電荷分布測定などを目的として液晶のボッケルス効果を用いることも多い。液晶を用いて得られる画像から、電界分布や電荷分布を計測するわけである。これなども画像と場の理論が直に結びついている一例である。
参考に、SHARPのプラズマアドレスディスプレイを示しておく。
 |
また、電子写真装置などは感光体表面に電荷分布を形成し、その電位像をトナーという電荷粒子で可視化するのであるから、電磁場を用いて画像形成をしているわけである。だから、場の理論を持ちこむのは至極当然であり、有用性も非常に高いだろう。そういった視点で考察してみたのが、
である。 同様に、画像圧縮に関しても、画像形成の物理性に着目することで実現できる場合も多いと思うのであるが、それは次回にしておく。