2000-01-30[n年前へ]
■ソフマップでお買い物 
磁界の可視化とバーコード
前回、
で「マグネビュアー」を使って磁界の可視化をして遊んでみた。今回はその続きである。ソフマップの磁気カードの中に書き込まれている磁気データを可視化して調べてみるのである。磁気カードには、
- 銀行のキャッシュカード
- クレジットカード
- テレホンカード
- オレンジカード
まずは、ソフマップカードの写真を示してみよう。これがソフマップで買い物をするたびにお世話になるソフマップカードである。
 |
この写真からではどこにデータが書き込まれているのかわからない。そこで、「マグネビュアー」の登場と言いたいところであるが、残念ながら今回は「マグネビュアー」は登場しないのである。「マグネビュアー」はとても便利なのであるが、さすがに磁気カードの磁気データを読もうとすると分解能が不足する恐れがある。
そこで、代打選手に登場願うことにした。代打選手はキヤノン製のLBPのトナーである。以前、
の時に「トナーはクーロン力で制御されて画像を作るのだ」という話があった。キヤノン製の白黒のLBPではクーロン力に加えて磁気力を使ってトナーを制御している。なので、キヤノン製の白黒トナーは磁性体粉末ということになる。テレホンカードが出た頃はキヤノン製のトナーを使ってデータを読み出していた人も多いはずである。みな、テレホンカードの表面を削りトナーを振り掛けていたのである。というのは、聞いた話であり、実体験に基づくものでは絶対にない。神に誓っても良い。その頃にキヤノン製のトナーを使い倒していたということは絶対にないのである。しかも、その数年後に(以下略)。
それでは、磁性体の微少粉末であるトナーをソフマップカードに振り掛けてみよう。
 |
ソフマップカードの磁気データが可視化されたのがわかると思う。磁気によるバーコードが見えるだろう。これがソフマップカードに書き込まれている磁気データである。
とはいえ、トナーの付着具合にムラがある。それは私が雑に実験を行ったからである。こんなにムラがあっても磁気コードが判別できるかどうか疑問を持たれる方も多いと思う。しかし、
- 読む方向に対して垂直な線が多い
- 読む方向に対して水平な線は少ない
そのようにして、ノイズを減らし、S/N比を上げた画像を示してみる。
どうだろうか、驚くほど綺麗になっているのがわかると思う。まさか、と思われるかもしれないが本当である。
さて、これはソフマップカードの磁気データの全体像であるが、もう少し拡大したものを以下に示す。
 |
極めて明瞭に磁気データが可視化されているのがわかると思う。これはトナーを振りかけて、1万円ちょっとのスキャナ(CanonのUSB接続の安物スキャナ)で読み込んだものに対して先の処理をしただけである。これほど明瞭になるのも、全て1次元バーコードの特徴のおかげである。磁気ヘッドの制作などをしなくても良いのである。
磁気カードの記録密度は銀行統一仕様(NTT)でもISO3554でも8.3bit/mm=211bit/inchであるから、最近の600dpi(dot/inch)程度のスキャナーであれば十分磁気データの画像読みとりが可能である。
それでは、もっと拡大してみる。拡大する部分は上の画像の右の辺りである。すると、このようになる。
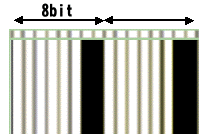 |
データ間隔がわかりやすいように、ここでは矢印や文字を書き入れている。この画像を見ると、磁気データは規則的な細かい周期性を持ち、その周期でいうと8つ単位でさらなる周期性があるように思われる。つまり、8bitをひとまとまりとしたデータが書き込まれているように見える。例えば、上の画像では
- ( 白、白、白、白、白、白、黒、黒 ) x 2
- ( 00000011 ) x 2
- ( ああああああたた ) x 2
複数枚のカードのこの部分を比較してみれば、比較的容易にデータ構造は解析することができるだろう。また、一枚のカードからでもカード番号などの数字と磁気データを比較することにより、解析することはやはり困難無しに解析できると思うのである。と、思うわけではあるが、あまりやりすぎるのはマズイと思われるので、今回はこれまでにしておく。
2000-01-31[n年前へ]
■落ちゆくエレベーターの中…で悩みます? 
無重力の理想と現実(仮)
今日もまた「ちゃろん日記(仮)」を読みに行くと、何とも面白い話があった。
である。この「ちゃろん日記(仮)」は「疑問とそこに隠れている真実を見つけだす感覚」に満ち溢れている、と私は思うのである。面白すぎである。さて、今回の話は、エンパイアステートビルでエレベーターが落ちたっていうけど、落ちていくエレベーターの中の人は
- 床に張り付く
- 天井に張り付く
- 宙に浮かぶ
「ほんとう〜にそうか? ほんとう〜にそうか?」
こういういかにも教科書に載っていそうな話には、時として落とし穴がある。教科書に書いてあるのは理想的で単純化した場合の結果である。それを鵜呑みにすると間違えてしまうことになる。極端に言えば、教科書に書いてあるような理想的な状態はほとんど存在しないので、教科書に書いてあるような現象はそうそう再現しない、ということになる。
ピサの斜塔から「落下の実験」を行ったのはガリレオ・ガリレイであると思っていると間違いである、というのは少し違う例になってしまうか。
久しぶりに思い出したが、私の所属していた研究室では重力測定は大きな柱であった。そして、確か大学院の入試問題の内の一題は、まさに
「落ちていくエレベーターの中の人達に働く力を精密に論ぜよ」であった(簡単に大雑把に言えば)。私はちゃんとこの問題を解けた覚えがない。いや、はっきり言えばずいぶん悩んだ覚えしかない。ってことはいまいち解けなかったのだろう。なので、「落ちていくエレベーターの中の人達は無重力状態である」と聞くと、「ほんとう〜にそうか? ほんとう〜にそうか?」と歌いたくなる。
研究室関連では、絶対重力測定を行う研究をする人達もいたわけである。絶対重力(加速度)測定は自由落下する物体の運動を測定して、重力加速度を測定するわけであるが、そう簡単に物体は自由落下してくれないのである。簡単な実験で物体を自由落下させて重力加速度を測定してみるとわかるが、大雑把な実験(自分の家ですぐできる程度の)では一桁ちょいの精度しか出ない。一桁ちょいの精度しかでないということは、(例えば)体重が10%弱程度になったように感じるかもしれないが、それは無重力ではない。体重が60kgの人であれば、6kgも感じてしまうのである。(雑な話だが。)
空気中を落ちてくる雨だってそうだ。もし、雨が自由落下を続けていたらものすごいスピードになって、雨に打たれるのは命がけになってしまう。しかし、実際にはそんなことはない。空気抵抗で速度は飽和してしまい、自由落下状態ではないからである。
さて、本題である。果たして、
例えば、
- 若井研究室の研究概要
- http://mech.gifu-u.ac.jp/~wakailab/research/Basic/base_h.html
北海道の上砂川町にある施設(JAMIC)で、490m落下させることにより、10秒の無重量環境が得られます。落下中は空気抵抗を受けるので、落下カプセルを二重構造にし、空気抵抗を無視できるように工夫してあります。と、記述されているように、実際には工夫をこらさなければ無重力状態は実現できないのである。絶対重力系などでも空気抵抗を無視するために、投げ上げて往復運動を測定するなどの工夫がいるのである。
と、言葉だけで書いてもしょうがないので、適当な計算でもしてみる。いや、もちろん、実験をするのが良いわけであるが、面倒だし…
まずはエレベーターには、
- 何の抵抗も働かない
- 空気抵抗とワイヤーの抵抗が働く
そして、エレベーターの中の人には空気抵抗は働かないとした。エレベーターの中の空気と人の速度差はほとんどないからである。また、エレベーターは人よりもはるかに重く、人の重さはエレベーターの運動に何の影響も及ぼさないと近似した。
その計算の結果を以下に示す。これが落ちていくエレベーターの軌跡である。抵抗のない場合が(赤)で抵抗のある場合が(青)である。エレベーターが落ち始めてから30秒後までの軌跡である。
 |
理想的な場合(赤)に比べて、抵抗のある場合(青)の落ち具合が鈍っているのがわかると思う。それでは、もっと時間が経った場合はどうだろうか?それを次に示す。エレベーターが落ち始めて300秒後までの軌跡である。つまり、五分間もこのエレベーターは落ち続けているのである。落ちた距離は理想的な場合で40kmの深さに達している。すごいエレベーターである。こんなに落ち続けていると、すでに重力加速度が一定とは言っていられなくなる。
 |
ここまでくると、抵抗のない場合(赤)と抵抗のある場合(青)では全然違う軌跡になっている。抵抗のない場合(赤)では放物線そのものであるが、抵抗のある場合(青)では一定の速度になっている。
それでは、エレベーターがこのような状態になった時の、エレベーターの中の人に働く加速度(と実際の加速度の差分)を示してみる。これを見れば、落ちていくエレベーターの中の人が無重力状態であるかどうかがわかる。まずは、300秒後までの変化を見てみる。
 |
理想的な場合(赤)はずっとゼロすなわち無重力状態であるが、抵抗のある場合(青)は無重力状態は最初だけで、50秒後位には通常の状態に戻ってしまっている。最初の部分をもう少し拡大してみる。次に示すのは、3秒後までの落ちていくエレベーターの中の人に働く重力加速度(と実際の加速度の差分)である。
 |
これを見ると、あっという間に人は無重力状態ではなくなっているのがわかると思う。
というわけで、先の三つの選択肢、
- 床に張り付く
- 天井に張り付く
- 宙に浮かぶ
先日みたニュースのエレベーター落下実験の中で、中にいた男性リポーターが、落下しながら「ひぃ?」とアオ向けになった状態で床にハリ付いていたからなのです。という実際の現象が正しいのである(いや、もちろん状況はかなり異なるが)。「頭の中だけ」で考えたことというのは大抵の場合間違ってしまう。(もちろん、今回の「できるかな?」の話もその例外ではない)
そして、その後に、
ありはきっと、速度がそこまで充分でなかったのと、もしやのトキのために、男性リポーターに安全な姿勢をとらせていたタメだと思われます。とあるが、実際問題として「速度がそこまで充分」になることは未来永劫ないわけである。だから、(私の中では)エレベーターの中の男性リポーター氏は床から浮かぶことはないのである。
こういうのは、結局考える人の数だけ答えがあるのだと思う。もし、その内のどれが真実に一番近いかどうか知りたければ、実験すれば良いだけの話だし。
2000-02-13[n年前へ]
■競馬の写真判定とパノラマ写真 
パノラマ写真と画像処理 Part.2
前回 、
の時にi_matさんから頂いたメールを紹介した。i_matさんは- I*MAT The HomePage (http://www.nsknet.or.jp/~i_mat/ )
- atoz@gol.com (http://www2.gol.com/users/atoz/index.html )
さて、前回
これらのソフトのStack-Slice機能を用いれば「複数画像(動画)からの走査線抽出」ができる。その使用例と、その面白い座標軸変換について考えてみたい。と書いた。今回もまた「数日後には登場」と言った割には時間が経っているような気もする。しかし、ここのところ文字通り忙殺されていたのである。と、言い訳をしながら今回この作業をやってみることにした。しかし、このページは少々重くなってきた。まして、走査線の抽出の話は使用画像が多くならざるをえない。そこで、次回、詳しく使用例を紹介することにする。
よく、次回登場と言ったまま数ヶ月経つことがあるが、今回は大丈夫である。少なくとも数日後には登場することと思う(多分)。
まずは、
- 「複数画像(動画)からの走査線抽出」
- 「座標軸変換」
以下に示す連続の画像は競馬のゴール地点に競走馬が到着した瞬間である。「馬に見えない」という人がいたら、それは目がおかしい。誰がなんと言おうとこれは馬である。馬と鹿の区別がつかない人は馬鹿と呼ばれるが、これはとにかく馬なのである。
 視野の中に馬がもっと入ってくる。
視野の中に馬がものすごく入ってる。 |
さて、このビデオカメラで撮影された画像は例えば以下のようなものである。
 |
撮影された各時間の画像から、この画像の赤で囲んだところを抽出し、並べたらどのようになるだろうか?
それはこのようになるだろう。よくある競馬の着順判定写真である。
 |
一見、これまで眺めてきたビデオカメラで撮影された画像と同じように見えるが、全く違う。ビデオカメラの撮影画像の動画中における、複数画像間の「位置」は全く変化していない。変化しているのは「時間」だけである。
だから、このような赤い長方形の画像を並べた方向というものは「時間軸」を意味しているのである。それを、下の画像に示してみる。
 |
この画像は縦方向は「空間軸」であるが、横方向は「時間軸」なのである。ビデオカメラの画像が縦横共に「空間軸」を示しているのに対し、その一軸を「空間軸」から「時間軸」に変換したものなのである
この競馬の着順判定写真の場合、カメラは空間に固定され「時間軸に変化するもの」を撮影していた。だから、このように各画像から一部を抽出して並べると、それは「時間軸」に対する変化を示すものを得ることができる。
また、例えば実験条件を変えたときの計測画像に対して「各画像から一部を抽出して並べる」ということをするならば、それは「空間軸」x「実験条件」というものを表す画像を得ることができる。
それでは、時間的には変化しないものを、ビデオカメラで撮影する方向を変化させながら撮影したらどうなるだろうか?例えば、ビデオカメラを下のようにして360度回転させながら撮影をしてみるのである。
 |
この場合撮影画像の各画像は撮影方向角度が異なるわけである。従って、先ほどのように一部分を抽出して並べると、一方向は「空間軸」であり、もう片方の軸は「撮影方向角度」になる。結局当たり前ではあるが、ある位置から眺めた周りの景色が得られるわけだ。
これが、前回i_matさんの要望していた
- 8ミリビデオを横倒しにして、 モーター回転するヘッドでぐるりと360度撮影し、
- その撮影した動画ファイルの、各フレームから走査線にして数本分を抽出し(インターレースで256本のうちセンター128本目の前後数本の走査線分)、
- それを貯めて1枚のjpgファイルにする、
- そのJPEG画像をMakeQTVRPanoramaの入力にして、パノラマムービーを作る、
それでは、その作業を実際にしてみようと思う。i_matさんから送って頂いた動画ファイル
を使い- 動画から静止画に変換し(走査線の狭間-1/60秒の世界を目指せ- (1999.07.08) 参照)、
- Image PC(NIH-imageをWindowsに移植したもの)で、走査線の一部を抽出し並べた静止画を作成する
もういきなり結果を出してしまおう。これが、「動画ファイルから走査線を抽出し、パノラマ写真にしたもの」である。
 |
おや?何が何だかわからない画像になってしまっている。変なモザイクがかかったみたいな画像になっているし、グレイ画像である。参考までに、先ほどの動画から手作業でパノラマ画像を作成したものを以下に示す。上の画像と比較してみると画像の示すものの対応がわかるだろう。
 |
さて、今回の実験結果が
- 変なモザイクがかかったみたいな画像になっている
- グレイ画像である
まず、
- 「グレイ画像」になっている理由
そして、「変なモザイクがかかったみたいな画像になっている」のは(動画中の)各画像から走査線をそれぞれ一本しか抽出しなかったからである。だから、横方向(カメラの撮影方向角度)のデータが足りないのである。そのため、モザイク画像のようになってしまったのである。
本来、抽出する走査線の数は、カメラの回転速度に応じて増やしてやらなければならないわけであるが、それが上手く合っていなかったのである。また、今回の画像を見て頂くと判ると思うが、動画ファイル自体も、実は一秒辺りのフレーム数が間引かれたものとなっている。それにより、抽出する走査線の数が一本ではますます足りなくなってしまっていたのである。
というわけで、今回は「失敗した」と言わざるをえない。何か、前回は「簡単である」などと言い切ったような気もするが、それはきっと気のせいであろう。
やはり、これは適当にあるもので間に合わせ仕事をしようとしたせいかもしれない。いつの日か「mov2panorama.exe」を作成し、必ずや必ずや再挑戦をするつもりである(Macでやるのは少しあきらめモード)。
2000-02-19[n年前へ]
■携帯電話の同時性? 
競馬の写真判定とパノラマ写真 その後
先日
を書いてから面白いメールを頂いた。その一部を抜粋すると、小生は超音波を利用した新しい流体場測定を行っていますが、この方法で得られるDataは空間1次元時間1次元の2次元データです。従って得られるのは、このページにあったような画像が直接得られるわけです。とある。この方法といくつかの結果を発表してから、あちこちからコンタクトがありましたが、その中の一つが、NYのSirovichという高名な流体力学者からの手紙でした。彼はいわゆるSnapShotを、逆に小生のデータから構築できないか、というのです。
今このWebでされたことの逆をしたいというわけです。流れの空間構造を解析するために使いたいのです。残念ながらこれは、以下に少々説明するように、原理的に無理な話で断らざるをえませんでした。
つまり、時間軸に速度をかけて空間軸に変換できればよいのですが、流体場はそれ自身が速度分布を持っていますから、一体何を使えば良いのかが定まらない。
電磁波の場合には光速が一定ですから、時間情報から空間情報を得ることができますが、古典流体力学では不可能なのです。工学的には平均流速を使って、時間-空間の変換をしますが、それはインチキとまでは言わないまでも、便宜的なも
のでしかありません。このWEBの中での例では、馬?の速度のみであとは静止しているので、可能でし
ょう。
「馬?」という箇所に、私との意見の相違があるようだ。私が明らかに「馬」であると言い張っているものに疑問を持たれているような気がするのであるが、今回そこは気にしないでおく。
なるほど、音波や電磁波などを使って計測を行い、得られた
- 空間(あるいは量)-時間
- 空間(あるいは量)-空間
- 海の中の魚を探知する「魚群探知機」
- 気象状況を計測する「気象レーダー」
- 固体の中の電荷分布を計測する「電荷分布測定装置」
「魚群探知機」は超音波を水中に発信して、その反射波が刻々と帰ってくる様子から、(超音波の速度を用いて、空間位置に変換した後に)障害物(ここでは魚群)の様子を計測するものである。「気象レーダー」も電波を使って同様に雲の分布などを測定する。
「電荷分布測定装置」の場合は、(例えば外部電界を印加し)電荷を持つ個所を振動させてやり、その振動がセンサー部に刻々と伝わってくる様子から(あぁ、なんて大雑把な説明なんだ)、(固体中の弾性波の速度を用いて、空間位置に変換した後に)固体の中にどのように電荷分布が存在しているかを計測するものである。
と、文章だけでは何なので、WEB上から、それらの計測器を用いた場合の計測例を示してみる。
下が魚群探知機である。リンク先は
である。 |
また、この下は空間電荷測定装置である。これなども、とても面白いものだ。リンク先は
である。 |
さて、こういうことを、調べてみるだけではしょうがない。自分でもそういう計測をしてみたい。
そこで、次のような実験をしてみようとした。
- 部屋の中に複数の「音の発信源」を配置する。
- 複数の「音の発信源」から同時に音を発する。
- それをPCで収録する。
- 音声が「音の発信源」からPCに到達するまでの時間を解析する
- 複数の「音の発信源」の位置を計測する。
そこで、安易にも時報を使おうかと考えてしまった。しかも、数があって手軽ということで、携帯電話を使おうとしたのである。
しかし、複数の携帯電話を集めて、117に電話して時報を同時に聞いてみると、とても同時どころではない。てんでばらばらなのである。電話のスピーカーから流れてくる時報のタイミングには結構ズレがあるのである。
携帯電話の間には結構同時性がないのだ。また、固定電話とも比較したが、固定電話よりも時報が速いものもあれば、遅いものもあった。
そこで、複数の携帯電話を聞き比べた結果を以下に示してみたい。この写真中で左の携帯電話ほど時報が先に流れており、右になるほど時報が遅れているのである。一番早い左と、一番遅い右では一秒弱の違いがあった。
 |
また、参考までに、家の固定電話と携帯電話の時報を一緒に聞いたサウンドファイルを示しておく。
この携帯電話は先に示した画像の一番左である。つまり、先の携帯電話群では一番時報が早かったものなのである。しかし、家の電話よりは一秒弱遅かった。ということは、家の固定電話と先の一番遅い携帯電話では時報の時間にして2秒弱の違いがあることになる。 そして、「家の固定電話と携帯電話の時報を一緒に聞いた音の変化」をスペクトログラムにしたものを以下に示す。
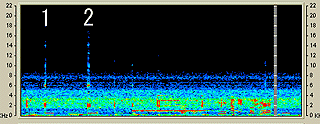 |
水平軸が時間軸であり、時間は左から右へ流れている。また、縦軸は音の周波数を示している。ここでは、「1」で示したのが家の固定電話の時報であり、少し遅れて「2」の携帯電話の時報が聞こえているのが見てとれる。
よく時報を確認することはあるが(実は私はほとんどないのだが...)、携帯電話・PHSで時報を聞く限り、秒の精度はそれほどないようである。また、勤務先の固定電話は先の携帯電話群と比べても遅い方であった。それは少し意外な結果であった。
今回調べた「携帯電話の同時性のなさは」は常識なのかもしれないが、電話の時報で時計を合わせるのはあまり精度が出ないやり方であることがわかっただけでもよしとしよう(別に実験を途中で投げ出した言い訳ではないけれど)。
今度、TV(衛星TVなども遅延時間を考慮した時報の放送を行っていると聞くし)やラジオを用いて当初計画していた実験を行おうと思う。その際には、時報がPCに到達する時間のズレで「音の発信源」までの距離を計測し、左右のマイクでの違いを計測することにより、「立体音感シリーズ」のように「音の方向」を得てみたい。
というわけで、話が「立体音感シリーズ」に繋がったところで、今回は終わりにしようと思う。
2000-03-19[n年前へ]
■一家に一台、分光器 
ハサミとテープで「できるかな?」
いきなりであるが、分光器を作りたい。光を波長別に分ける機器である「分光器」である。とある実験をするために、分光器が必要なのである。その「とある実験」の影には、大きな野望があるのだが、まだ明らかにする訳にはいかない。とりあえず、色の話題を考えるときに分光器があると便利だから、という理由にしておきたい。
どうやって分光器を作るか考えてみる。普通であれば、グレーティング(回折格子)やプリズムといったものを使うことになるだろう。家の中を探してみれば、プリズムなどもあるはずなのだが、WEBで情報を探してみると面白い情報があった。
- CDを利用した分光器の製作
- ( http://www.sunfield.ne.jp/~oshima/omosiro/spec.html )
- 遮光フィルムを用いた分光器の製作(その1)
- ( http://www.asahi-net.or.jp/~DJ9K-SMZ/goods/spectre/spectre.html )
次に示すのが、HIRAX一型分光器である。ハンディ・超軽量の優れものだ。テープとハサミと去年のカレンダーを駆使し、フリーハンドで作成した、製作時間20分の大作である。どうも私の仕事はテープとハサミを駆使することが多い。それは、ハードでもソフトでも、どちらでも同じことである。出来の悪いノッポさんである。
 |
左下がスリット部になっている。中央上の折れ曲がっている部分にグレーティングが配置している。次の写真を見るとグレーティングがあるのが判ると思う。HIRAX一型分光器の内部は散乱光を防止するために、黒く塗ってある。しかし、下の写真を見れば判るように、グレーティングの周りの片側は塗り忘れてしまった。まるで、「耳なし保一」である。
 |
こちらの開口部から目で覗くなり、デジカメで撮影するなりするのだ。そうすれば、スペクトルが確認できる、というわけである。
例を示してみたい。グレーティングが曲がっているせいで、スペクトルが歪んでいるし、スリットが結構太いし、サイズのせいもあってスペクトルの分解能はそれほど高くない。しかし、結構きれいな映像を得ることができる。まずは、太陽光のスペクトルを見てみる。
 |
これはデジカメで撮影したものである。スリットが太いので確認しづらいのだが、太陽光のフラウンホーファー線(FraunhoferLine)の一つHβ吸収線が486nm(ここでは水色の中央部)辺りに見えるような気がしないだろうか? いずれ、スリット幅を小さくして、もう少し精度の高い実験をしてみる予定である。
さて、次の例は「自宅の蛍光灯のスペクトル」である。
 |
- 黄色、橙色 579、577nm
- 黄緑色 546 nm
- 水色 436 nm
- 紫色 408、405 nm
 |
目で覗いたり、デジカメで撮影したりするのも面倒なので、可視・赤外領域に感度を持つCCDボードを秋月で買ってきた。次回、このCCDボードを取り付けて見る予定だ。そして、定量化をしてみたいのである。そして、ある野望のためにせっせと実験を続けていく予定である。

