1998-12-27[n年前へ]
■Wveletで周期解析をしてみる 
音声・地震などの1次元信号や、画像等の2次元信号処理の解析というのはなかなか面白そうだ。そこで、周期ムラに対してWaveletをかけて周波数解析をする練習をやってみたい。また、短時間フーリエ変換とWaveletの比較もしてみたい。音声・地震などのデータはまた別にやってみることにして、今回は画像データを扱うことにする。ただし、いきなり2次元も何なので、画像データの周期(つまり1次元的な振動)に注目して、解析を行ってみたい。
まずは、「周期ムラのある画像」と「周期ムラのない画像」の2種類の画像を作成する。画像はいずれも数式を用いて作成した。X方向に変化する縞模様であり、表.1のような演算式になっている。一応、2次元画像ではあるが、Y方向にはなんの変化もない。2つの数式を見比べてみると判るが、いずれも2項からなり、低周波数のSinと高周波数のSinからなっている。「周波数ムラのある画像」では、その低周波数のSinの中にさらにSinがあるので、周波数がある周期で変化していることになる。一見、「周波数ムラのない画像」の方でも低周波数のSinの内部にさらにSinがあるように見えるが、0が掛けられているので、実際には存在しないのと同じである。
| 2つのSinからなり、その一方のSinの周期がムラ(一定の周期)をもっているもの。第二項目のSinの内部にさらにSinを入れることにより、周波数ムラを作っている。 | 2つのSin波からなり、どちらの周期も正確なもの。第二項目のSinの中のSinは0をかけてあるので、何ら影響を及ぼさない。 |
そのような数式に基づいて作成した画像を図.1に示す。なお縦軸がX軸であり、横軸がY軸である。図.2(b)では周波数ムラはないが、2つの周波数成分から作成されているため、うねりが生じている。
 | 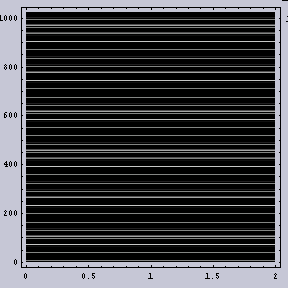 |
まずは、Wavelet変換である。図.2がその結果である。縦軸が周波数を示している。縦軸の上方向が高周波を示し、下方向が低周波を示している。また、横軸が原画像のX方向である。白は強度が小さいことを示し、黒は強度が強いことを示している。
いずれの画像も2つの周波数成分からなることが一目瞭然である。また、図.2(a):「周波数ムラのある画像」の方では低い周波数成分の方が、さらにある周期で周波数が変化していることがわかる。
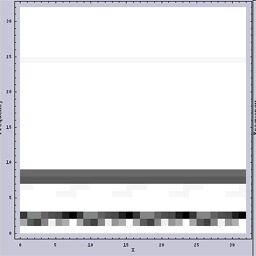 |  |
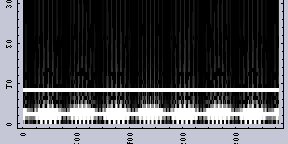
同じWavelet変換でも異なるFilterを用いてみると、結果は異なる。例えば、図.3がその例である。こちらの方が「周波数ムラ」がどのように生じているかを見るにはいいかもしれない。
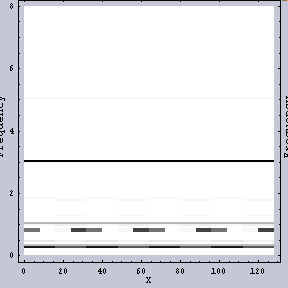 | 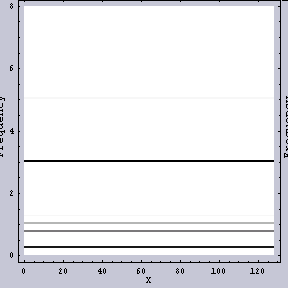 |
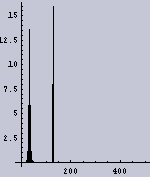
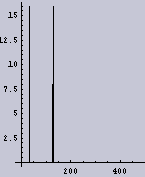
それでは、Wavelet変換ではなくて、フーリエ変換を用いて周波数解析を行ってみる。先ほどの1次元データの全領域に対してフーリエ変換をかけてみる。その結果が図.4である。ここで、横軸が周波数を示し、右側が高周波数を示し、左側が低周波数を示している。縦軸は強度である。
このフーリエ変換の場合も、2つの画像が2つの周波数成分からなり、図.4(a):「周波数ムラのある画像」では低周波数成分がぶれているのはわかる。しかし、その周波数ブレがどのようなものであるかまでは、わからない。
 |  |
なお、単純のためにウィンドー処理はしていない。そのために悪影響は当然出てしまう。
 |  |
単なる全領域にわたった周波数解析と、位置と周波数が同時にわかる解析の違いは非常に大きい。使いこなすのはなかなか難しそうだが....
1999-02-27[n年前へ]
■画像ノイズ解析について考える 
考える理由
画像ノイズ解析を目的として、2次元フーリエ変換を用いて周波数解析をすることが多い。かねがね、このやり方について疑問を感じていたので少し考えてみたい。その疑問とは次のようなことである。
- 通常の2D-FTでは、入力データ全領域での周波数解析を行う。従って、単発のパルスのようなノイズはバックグラウンドに埋もれてしまい、結果にはなかなか出てこない。
- 同じ理由で、2D-FTでは位置と周波数解析を同時に行うことができない。(もちろん、短時間フーリエ関数を使えば、そのような測定は行うことができる。)
- また、ホワイトノイズのようなフラットな周波数特性を持つノイズもバックグラウンドを押し上げるだけの効果しか持たないため、解析をしづらい。
2D-FTと2D-Waveletの例
はじめに、2D-FTと2DWaveletの例を挙げる。まずは2D-FTである。 |  |  |
このように、2D-FTの結果というのは周波数(X,Y両方向)と振幅がわかる。ここでのスクリーン角のような周期性を持つものの解析にはフーリエ解析というのは極めて有効である。店で見かけるインクジェットプリンターもヘッドの移動による周期ムラが激しいが、このようなムラに対してフーリエ変換を用いた周波数解析を行うのは正当であり、有効だろう。
それでは、同じ画像に2D-Waveletをかけてみる。2D-Waveletの結果は位置と周波数強度分布情報(ホントは違うのだが)が両方出てくる。位置情報が2次元で周波数強度分布情報が1次元であるから、合わせて3次元である。そのため、表示に一工夫いる。
第一段階として高周波成分から調べてみる。すぐにこの結果の意味がわかるだろうか?
 |  |
| 高周波のX成分 | 高周波成分 |
| 低周波成分 | 高周波のY成分 |

もう何分割かしてみる

なお、フーリエ変換では基底関数としてSinが用いられるが、Wavelet変換では基底関数としていろいろな関数を使うことができる。今回はDaubechiesの4次のものを用いている。下がその形である。
 |
ドットのノイズを解析してみる
それでは、今回の本題に入る。以下が原画像である。左が「2つの大きなドットからなる」画像であり、右がそれにノイズの加わった「ノイズ」画像である。ここでノイズはホワイトノイズを加えているつもりである。ドットは周期性を持つデータだが、ノイズ自体は周期性を持たない所がミソである。また、ここで言う「ノイズ」とは現実の現象とは何ら関係がない。単なる例えである。 |  |
 |  |
右のノイズの加わった画像の2DFTの結果では、広い周波数領域で強度が上がっている。しかし、下の鳥瞰図で示した(私は立体が好きなのだ)方でもわかると思うが、バックグラウンドが持ち上がっているだけである。いずれにせよ、あまり左右の間で違いはない。今回のような64x64の画像ではなく、もっと大きい画像ではその違いははより識別不能になる。
 |  |
 |  |
1999-02-28[n年前へ]
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
 |  |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
 |  |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 |  1階微分 |
 13/10 (=1.3)階微分 |  15/10 (=1.5)階微分 |  17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
1999-05-03[n年前へ]
■「私と好みが似てる人」 その2 
ログ解析の6ヶ月点検
本サイトが公に公開されるようになってから6ヶ月経った。新車でも購入してから半年経てば、6ヶ月点検があるのだから、本サイトについても6ヶ月点検を行ってみたい。
まずは、週別のアクセス量変動を挙げてみる。
 | Overall Accesses |
アクセス数は割に順調に伸びているようである。1999/02下旬辺りにネットワーク不調とログ解析失敗などによるデータ欠損が見られるが、それ以外ではほぼ線形に増加している。1999/4上旬に増加の傾きが変化しているのはinfoseekにページを登録したことによるものと考えられる。
次に、時間別アクセス量である。以下に示すのは、1999/4/18-24の時間別アクセス量である。
これを見ると、深夜3時位にアクセス数がぐんと減ることがわかる。深夜3時位に眠りにつく人が多いのだろうか。
そして、早朝5時過ぎからアクセス数が増えていくことがわかる。5時過ぎくらいから活動を始める人も多いようだ。そして、昼の12時辺りにひとつピークがある。これは、企業の昼休み時間にアクセスしている人達によるものだろう。次に15時位に大きなピークがある。これは、何だろうか?まさか、おやつの時間ではあるまい。企業ユーザーが一服しているのだろうか?小さい18時辺りのピークも、企業ユーザーの就業時間の終わりを示すものと思われる。
そもそも、こういった昼間の時間別アクセス数から見えてくるユーザーというものは、時間に縛られる企業ユーザーになってしまうのだろう。
 |
さて、次はアクセス数のサイトランキングである。ただし、ここでのサイト=IPアドレスであり、ドメイン解析は行っていない。したがって、同じドメインからアクセスがあっても、IPアドレスが異なれば違うサイトとして計算している。そのため、proxyを使っているような所が、ランクインしやすいということになる。もちろん、proxyを使っていれば、実際よりアクセス数は少なくなるわけだが、今回の比較においては、明らかに同じサイトと判断される分有利なのである。
それでは、最近4週間分のトップ10を示してみる。
| Rank | 4/18-24 | 4/11-17 | 4/4-10 | 3/28-4/3 |
|---|---|---|---|---|
| 1 | KyotoPneT | MeshNet厚木 | 阪大レーザー核融合研 | KyotoPneT |
| 2 | 東大情報システム工学研 | キヤノン裾野 | Hewlett Packerd | キヤノン裾野 |
| 3 | セイコーインスツルメンツ | オーイーシー | キヤノン裾野 | 千葉大情報数理 |
| 4 | Fermi-lab | 岡山理科大 電子工学 | ホンダエンジニアリング | PSINet |
| 5 | OCN | 北大 電子科学研究所 | ベッコアメ福岡 | シチズン |
| 6 | アスキー | NTT PC-Com 諏訪 | 鹿児島大 情報工学 | 東北大加齢医学研 |
| 7 | 明治大学総合情報ネットワーク | ワコー | デジタルアーツ | 生協インターネット大阪 |
| 8 | RICOH | IIJ4U | 藤沢インターネット | 九州大学医 耳鼻咽喉科 |
| 9 | WEB静岡 | 龍谷大情報NetworkSystem | 通商産業省 | InfoPepper府中 |
| 10 | KansaiMultimediaService | OCN千葉館山 | アレスネット | DTI熊本 |
トップ1に4回中2回も位置しているのはKyotoPneTである。このサイトは京都周りのネットワーク総合体のようだ。色々集まっている分、アクセス数が多いのだろう。
それでは、週別にコメントをつけてみたい。
3/28-4/3 医学関係が2つランクインしている。おや、九州大学医学部耳鼻咽喉科と言えば、私の一番大好きな「今日の必ずトクする一言」で有名な「バーチャル耳鼻咽喉科」と同じサブドメインである。
4/4-10 通商産業省は公益機関のランクインが少ない中でなかなか健闘している。阪大レーザー核融合研究所はこの2週後のFermi研究所と関係あるのだろうか?
4/11-17 MeshNetの厚木からアクセスされている方が一位である。個人のアクセスというのは非常に嬉しい。この週は個人の方が多い。喜ばしいことだ。
4/18-24 常連だったキヤノン裾野が消え、RICOHがランクインしている。このあと、WEBページは会社の顔色- WEBページのカラーを考える 2 - (1999.04.26) でRICOHのWEBのデザインに苦言を呈しただけに、反応が気にかかるところである。おやおや、ASCIIもランクインしている。
それでは、3ヶ月前に「私と好みが似てる人」 - analog Windows版用のサブドメイン解析ソフトを作る- (1999.01.24) の時に調べたドメインランキングとの比較をしてみる(こちらは、ドメインランキングであって、今回のサイトランキングとは異なる。今回の場合、同じ人がアクセスしても、IPアドレスが異なれば、違う人としてカウントしていることになる)。
1: canon.co.jp (キヤノン)
2: sony.co.jp (SONY)
3: atr.co.jp (株式会社国際電気通信基礎技術研究所)
4: infocom.co.jp (日商岩井)
5: waco.co.jp (ワコービジネス)
6: odn.ad.jp (オープンデータネットワーク)
7: nttpc.ne.jp (ISP事業者向けネットワーク提供サービス)
8: att.ne.jp (日本AT&T株式会社)
9: saitama-u.ac.jp (埼玉大学)
10: kokushikan.ac.jp (国士舘大学)
今回と共通してトップ10入りしているのはキヤノンとワコーである。前回も今回も技術系のサイトばかりである。私が技術マニアであるからしょうがないか。それこそ、「私と好みが似てる人」達なのだろう。
次は「できるかな」内の人気ランキングである。こうしてみると、
- 本人が便利なものは、他人も便利(ex./dekirukana/server/)
- 本人はいまいちだが、読まれている(ex./dekirukana/java/)。
- 本人は気に入っているのに、人気がない(ex./dekirukana/harddisk/)。
#reqs: %bytes: last date: file-----: ------: --------------: ---- 4185: 18.07%: 99/05/15 07:49: / 13: 0.04%: 99/05/12 13:51: /? 1855: 2.18%: 99/05/15 02:33: /dekirukana/java/ 1093: 1.24%: 99/05/15 07:38: /dekirukana/server/ 839: 1.74%: 99/05/15 07:08: /dekirukana/snif/ 789: 0.68%: 99/05/15 04:01: /dekirukana/dorae/ 762: 0.58%: 99/05/15 02:36: /dekirukana/screensave/ 633: 0.83%: 99/05/15 05:32: /dekirukana/photoshop/ 623: 1.20%: 99/05/15 07:20: /dekirukana/whois/ 577: 0.99%: 99/05/15 04:20: /dekirukana/1999/ 543: 0.64%: 99/05/14 22:53: /dekirukana/tire/ 501: 0.80%: 99/05/15 01:55: /dekirukana/digicame/ 435: 0.52%: 99/05/15 00:51: /dekirukana/e55/ 435: 1.22%: 99/05/15 02:23: /dekirukana/ufo/ 427: 0.37%: 99/05/15 04:15: /dekirukana/ocilo/ 392: 0.43%: 99/05/15 06:53: /dekirukana/screensave2/ 373: 0.50%: 99/05/15 05:23: /dekirukana/fem2/ 321: 0.63%: 99/05/15 02:49: /dekirukana/wavelet/ 320: 0.56%: 99/05/15 05:28: /dekirukana/ekisyo2/ 279: 0.32%: 99/05/14 22:30: /dekirukana/hamaphoto/ 267: 0.37%: 99/05/14 23:25: /dekirukana/real97/ 264: 0.36%: 99/05/15 02:28: /dekirukana/karaoke/ 263: 0.16%: 99/05/15 02:25: /dekirukana/ocilo2/ 260: 0.41%: 99/05/15 01:15: /dekirukana/moire3/ 256: 0.81%: 99/05/14 21:07: /dekirukana/onkai2/ 256: 0.44%: 99/05/15 01:48: /dekirukana/sacchan/ 252: 0.29%: 99/05/15 05:52: /dekirukana/toolplus/ 247: 0.24%: 99/05/15 03:02: /dekirukana/server2/ 243: 0.63%: 99/05/15 00:17: /dekirukana/bunsukai/ 216: 0.42%: 99/05/15 06:52: /dekirukana/haidi/ 195: 0.06%: 99/05/15 00:24: /dekirukana/1999_2/ 194: 0.41%: 99/05/15 04:05: /dekirukana/kamogawa/ 186: 0.38%: 99/05/15 01:02: /dekirukana/bunpu/ 185: 0.39%: 99/05/15 04:21: /dekirukana/ufo2/ 185: 0.28%: 99/05/15 05:30: /dekirukana/ekisyo/ 180: 0.38%: 99/05/15 07:42: /dekirukana/moire2/ 171: 0.33%: 99/05/15 02:48: /dekirukana/wavelet2/ 169: 0.17%: 99/05/14 20:48: /dekirukana/rocket/ 164: 0.16%: 99/05/15 04:04: /dekirukana/dorae2/ 160: 0.31%: 99/05/14 15:03: /dekirukana/probe/ 155: 0.14%: 99/05/15 07:08: /dekirukana/tamago/ 144: 0.20%: 99/05/14 21:53: /dekirukana/onkai/ 141: 0.23%: 99/05/13 20:15: /dekirukana/ 126: 0.26%: 99/05/15 01:34: /dekirukana/harddisk/ 124: 0.18%: 99/05/15 02:03: /dekirukana/watari/ 122: 0.29%: 99/05/14 20:49: /dekirukana/webcolor2/ 121: 0.59%: 99/05/15 01:29: /dekirukana/moire/ 118: 0.10%: 99/05/14 14:08: /dekirukana/hori/ 118: 0.18%: 99/05/14 09:21: /dekirukana/bunsukai2/ 116: 0.10%: 99/05/14 21:05: /daily/9904.html 105: 0.19%: 99/05/15 07:34: /dekirukana/favicon/ 105: 0.24%: 99/05/15 06:29: /dekirukana/log9905/ 99: 0.20%: 99/05/14 20:49: /dekirukana/webcolor/ 98: 0.05%: 99/05/15 07:08: /dekirukana/photoshop2/ 79: 0.38%: 99/05/14 09:58: /index_e.html 61: 0.01%: 99/05/13 18:27: /dekirukana/fem2/math/ 46: 0.01%: 99/05/12 19:50: /dekirukana/fem2/math/indexlnk1.html 42: 0.07%: 99/05/12 19:53: /dekirukana/fem2/math/indexlnk4.html 37: 0.03%: 99/05/12 19:51: /dekirukana/fem2/math/indexlnk2.html 33: 0.08%: 99/05/13 18:28: /dekirukana/fem2/math/indexlnk3.html 32: 0.02%: 99/05/14 14:22: /dekirukana/toolplus/readme/readme.html 31: 0.05%: 99/05/12 19:54: /dekirukana/fem2/math/indexlnk5.html 25: 0.06%: 99/05/15 00:22: /dekirukana/harddisk/math/ 21: 0.03%: 99/05/12 19:49: /dekirukana/onkai/math/ 4070: 55.84%: 99/05/15 05:52: [not listed: 34 files]こうしてみると、興味が発散している作者であることがよくわかる。
次にログ解析をするのは、おそらく半年先だろう。 その時、健やかに育っているのだろうか?
2002-03-12[n年前へ]
■今日の面白かったこと 
 以前、何かの榊原教授のセミナーを聴いたときになんとも上手い話し方をするなぁ、と感嘆したので、そういう人の説明を直接聴ける貴重な時間は忙しいときだからこそ、ということで東京へ。
以前、何かの榊原教授のセミナーを聴いたときになんとも上手い話し方をするなぁ、と感嘆したので、そういう人の説明を直接聴ける貴重な時間は忙しいときだからこそ、ということで東京へ。
「あれ?」とびっくりするくらい聴いている人は年輩の方が多いが、そんなことはおいておき、今日「そーいえば、そーだったっけなー」と思ったのは、メキシカンハットがガウス関数の微分という一言だった。「MexicanHatでWavelet変換をかけるときは、ガウスの微分に分解している。もし、ガウス関数で表されるような現象であれば、それはその微分に展開している」という物理的な意味として使うのに面白いかも、と思ったのだった。結果的には、その一言を聴くためだけに行ったようなものだけど、コストパフォーマンスは悪くないかな。